Глава 2. Динамика §8. Законы Ньютона

c8.1. Модуль скорости лыжника при равноускоренном спуске с горы за t₁ = 4 с увеличился на v₁ == 6 м/с. Масса лыжника m = 60 кг. Чему равен модуль F_р равнодействующей всех сил, приложенных к лыжнику?

с8.2. Материальная точка массой m = 12 т движется в плоскости yОх так, что за время  = 1 мин проекция ее скорости на ось Ох уменьшилась на 18 км/ч. Какова проекция на эту ось постоянной силы F, приложенной к материальной точки?

8.3. Используя условие задачи 8.2, определить проекцию на ось Оy постоянной силы F, приложенной к материальной точке, если ее модуль равен 1,41 кН?

8.4.На рисунке представлена зависимость проекции силы, приложенной к материальной точке, от времени. Какова была проекция начальной скорости м.т. v_нх, если к концу четвертой секунды она имела проекцию скорости v_x(4) = 1м/с? Масса тела m = 1кг.

с8.5.На рисунке представлена зависимость координаты материальной точки от времени, являющаяся параболой (в начале координат находится вершина параболы). Какова масса материальной точки m, если в течение времени t₁ = 3 c на нее действовала постоянная сила F = 2 Н?

8.6. Найдите проекцию ускорения тела массой m = 0,25 кг на ось Оy, если в данный момент к ней приложена сила F = 3i +F_yj, причем модуль силы F = 5 Н.

8.7. Найдите проекцию ускорения материальной точки массой m = 0,5 кг на ось Ох, если в данный момент к ней приложена сила F = F_хi +8j, причем F = 10 Н.

8.8. Две материальные точки, массы которых m₁ = 1 кг и m₂ = 2 кг, взаимодействуют только между собой. Скорость первой м.т. со временем изменяется по формуле v₁ = (10  2t)i, а скорость второй м.т. в начальной момент времени v_2н = 0. Определите скорость второй м.т. через время t₁ = 5 с.

8.9. Первый парашютист падает с ускорением а₁ = 0,25g, а второй — с ускорением а₂₁ = 0,5g, относительного первого. Чему равна равнодействующая сил, приложенных ко второму парашютисту, масса которого m = 60 кг?

c8.10. Шахтная клеть массой М = 310³ кг начинает подниматься с ускорением а = 0,5 м/с². Определить: а) натяжение троса Т₁, при помощи которого поднимается клеть; б) натяжение троса Т₂ в начале спуска клети с тем же ускорением; в) натяжение троса Т₃ при движении клети с постоянной скоростью вверх и вниз.

8.11. Подвешенное к тросу тело массой m = 10 кг поднимается вертикально вверх, при этом сила натяжения троса Т₁ = 118 H. Каким будет натяжение троса Т₂ при движении тела вертикально вниз с таким же по модулю ускорением?

8.12. Лифт поднимается с ускорением a = -0,5g. Человек, находящийся в лифте, роняет мячик с высоты h = 1 м через время t₁ = 1 с после начала подъема. Через какое время  после начала падения мячик упадет на пол?

8.13. Два груза массами m = 0,2 кг и М = 4 кг соединены нитью и лежат на гладком столе (трением пренебрегаем). К первому грузу приложена сила F₁ = 0,2 Н, действующая вдоль направления нити, ко второму — в противоположном направлении сила F₂ = 0,5 Н. С каким ускорением а будут двигаться грузы и какова сила натяжения соединяющей их нити T?

8.14. Через невесомый блок, укрепленный на ребре призмы, грани которой образуют углы  и  с горизонтом, перекинута нить (см. рисунок). К концам нити прикреплены грузы массами m₁ и m₂. Найти ускорения грузов. Трением пренебречь.

8.15. Для системы тел, изображённой на рисунке, определить силу натяжения нити T и силу F, действующую на ось невесомого блока. Клин неподвижен, длина ребер а = 5 м, b = 12 м, угол  = 90, трение отсутствует. Массы тел m₁ = 10 кг и m₂ = 20 кг. Нижняя грань клина горизонтальна.

8.16.К концам шнура, перекинутого через блок, подвешены грузы m₁ = 50 г и m₂ = 75 г. Пренебрегая трением и считая шнур и блок невесомыми, а шнур нерастяжимым, определить ускорения, с которыми будут двигаться грузы, силу натяжения шнура и показание динамометра, на котором висит блок.

8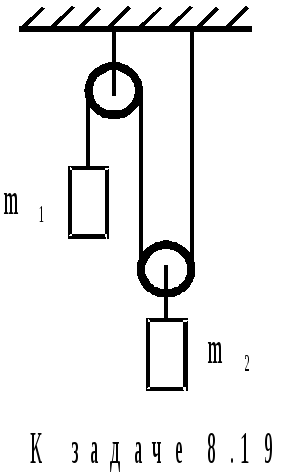.17.Две гири массами m₁ = 7 кг и m₂ = 11 кг висят на концах малорастяжимой нити, которая перекинута через блок. Гири вначале находятся на одной высоте. Через какое время t после начала движения более легкая гиря окажется на L == 10 см выше тяжелой? Массой блока, нити и сопротивлением движению пренебречь.

8.18. Два одинаковых груза массой М подвешены на невесомой и нерастяжимой нити, перекинутой через блок. На один из них положен грузик массой m. Определить силу f_д давления грузика на груз М и силу F, действующую на ось блока.

8.19. Найти ускорения a₁ и а₂ масс m₁ и m₂ и силу натяжения Т нити в системе, изображенной на рисунке. Массой блоков и нити и трением пренебречь.

8.20. Через неподвижный блок перекинута веревка, к одному из концов которой привязан груз массой m₁ = 64 кг. На другом конце повис человек массой m₂ = 65 кг, который, выбирая веревку, поднимает груз, оставаясь при этом на одном и том же расстоянии от пола. Через какое время t₁ груз будет поднят на высоту h = 3 м? Массой веревки и блока пренебречь.

8.21.Клин с углом наклона грани к линии горизонта  = 30 вращается вокруг вертикальной оси с угловой скоростью ω = 2 с^–1 и одновременно перемещается вертикально вниз с ускорением a = 2 м/с². На наклонной грани клина на расстоянии R = 0,5 м от оси вращения находится неподвижный относительно клина брусок массой m = 2 кг. Определите величину силы трения действующей между бруском и клином.

8.22. Груз, подвешенный к шнуру, движется равномерно по окружности в горизонтальной плоскости так, что шнур описывает коническую поверхность и отклоняется от вершины на угол  = 60. Определите величину ускорения, с которым движется груз.

8.23. Диск с закрепленным на нем стержнем (по оси диска) вращается вокруг вертикальной оси (см. рисунок). На диске находится шарик, прикрепленный к стержню нитью длиной L, составляющей угол  со стержнем. С каким периодом должен вращаться диск, чтобы шарик не отрывался от него?

8.24. Круглая платформа с закрепленным на ней стержнем (по оси платформы) вращается вокруг вертикальной оси с угловой скоростью ω = 4,0 с^–1 (см. рисунок). На платформе находится шарик массой m = 1,2 кг, прикреплённый к стержню нитью длинной L = 0,4 м. Угол наклона нити  = 60. Найти силу давления шарика на платформу.