§7. Движение по окружности. Плоское движение

7.1. За промежуток времени t = 10 с материальная точка прошла одну треть окружности радиуса R = 1 м. Определить среднюю путевую скорость и модуль средней скорости.

7.2. Две точки равномерно движутся по окружности, причем первая точка движется по часовой стрелке, вторая — против часовой стрелки. Период обращения первой точки Т₁ = 5 с, период второй точки Т₂ = 2 с. Найти время между двумя последовательными встречами точек.

7.3. Определить линейную скорость Земли v при ее орбиталь­ном движении. Средний радиус земной орбиты R = 1,510⁸ км.

7.4. Пропеллер самолета радиусом R = 1,5 м вращается при посадке с частотой n = 2000 мин^–1, посадочная скорость самолета относительно Земли v = 162 км/ч. Определить скорость точки на конце пропеллера u относительно Земли. Какова траектория движения этой точки?

7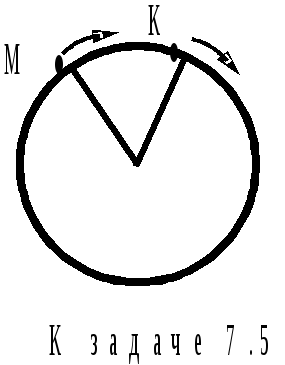.5.Две точки М и К движутся равномерно по окружности (см. рисунок) с угловыми скоростями _м = 0,2 рад/с и _к = 0,3 рад/с. В начальный момент времени угол между радиусами этих точек ₀ = /3. В какой момент времени эти точки встретятся?

7.6. Механические часы показывают время t = 4 ч. Через какой промежуток времени t₁ минутная стрелка догонит часовую?

7.7. Сколько разNв сутки встречаются часовая и секундная стрелки часов?

7.8. Тяжелый шарик на нити вращается в горизонтальной плоскости так, что нить описывает коническую поверхность. Определить длину нити L, если частота вращения шарика n = 0,5 с^–1, его центростремительное ускорение a_ц = 8 м/с² и угол отклонения нити от вертикали  = 45.

7.9. Мальчик вращает камень, привязанный к веревке длинной L = 0,8 м, в вертикальной плоскости с частотой n = 4 с^–1. В тот момент, когда веревка была расположена горизонтально, она оборвалась. На какую высоту h взлетит камень?

7.10. Пуля, летевшая горизонтально, пробила один за другим два диска, насаженных на один вал и вращающихся с частотой n = 10 с^–1. Расстояние между дисками S = 30 см. Найти скорость пули v между дисками, если угловое смещение пробоин φ = 9 и пробоины оказались расположенными на одинаковом расстоянии от оси вращения.

7.11. Стержень вращается вокруг оси, походящей перпендикулярно стержню через некоторую его точку. Скорости концов стрежня при этом равны v₁ = 1м/с и v₂ = 5 м/с. Угловая скорость стержня ω = 1 с^–1. Найти длину стрежня.

7.12. Найти радиус вращающегося колеса, если известно, что линейная скорость точек обода колеса в n = 2,5 раза больше линейной скорости точки, лежащей на расстоянии d = 5 см ближе к оси колеса.

7.13.Диск радиуса R катится без проскальзывания с постоянной скоростью v по горизонтальной дороге (см. рисунок). Найти ускорения точек A и B и скорости точек С и D относительно дороги.

7.14. Катушка с нитью катится по горизонтальному столу без проскальзывания. Внутренний радиус катушки r, внешний R. С какой скоростью v_О перемещается ось катушки O относительно стола, если конец нити тянут в горизонтальном направлении со скоростью v? Рассмотреть два случая (см. на рисунке пункты а и б).

7.15.Цилиндрический каток радиусом R помещен между двумя параллельными рейками. Рейки движутся в одну сторону со скоростями v₁ и v₂ (см. рисунок). Определить угловую скорость вращения катка и скорость его центра, если проскальзывание отсутствует.

7.16. Диск, радиус которого R, катится без скольжения с постоянной скоростью v. Найти геометрическое место точек на диске, которые в данный момент имеют скорости относительно Земли, модуль которых равен 1,5v.

7.17. Колесо, пробуксовывая, катится по ровной, горизонтальной дороге. Найти скорость центра колеса v_О, если модуль скорости его нижней точки v₁ = 2 м/с, а верхней — v₂ = 10 м/с, причем скорости этих точек направлены в противоположные стороны.

7.18. Шарик, радиус которого R = 5 см, катится равномерно и без проскальзывания по двум параллельным брускам квадратного сечения. Расстояние между брусками d = 6 см. За время t = 2 с шарик проходит путь S = 1,2 м. С какими скоростями движутся верхняя и нижняя точки шарика?

7.19. По горизонтальной плоскости катится без скольжения с постоянной скоростью v обруч радиусом R. Выразить модуль скорости различных точек обруча относительно плоскости как функцию угла  между вертикалью и прямой, проведенной между точкой прикосновения обруча с плоскостью и данной точкой обруча. Определить скорость v_Р точки Р обруча при  = 30.

7.20.Автомобиль движется со скоростью v = 60 км/ч. С какой частотой n вращаются его колеса, если они катятся по шоссе без скольжения, а внешний диаметр покрышек колес равен d = 60 см? Найти центростремительное ускорение а_цс внешнего слоя резины на покрышках его колес.

7.21. Два одинаковых диска расположены так, как показано на рисунке. Диск 1 неподвижен. На какой угол повернется диск 2, обойдя без проскальзывания один раз диск 1?

7.22.У диска 1 радиус R, у диска 2 радиус в два раза больше (см. рисунок). Диск 2 неподвижен. Сколько оборотов N сделает диск 1, обойдя без проскальзывания один раз диск 2?

7.23.Стержень шарнирно соединен с муфтами А и В, которые перемещаются по двум взаимно перпендикулярным рейкам (см. рисунок). Муфта А движется с постоянной скоростью v_A = 30 см/с. Найти скорость v_B муфты В в момент, когда угол ОАВ = 60.

7.24. Стержень АС движется так, что в данный момент времени скорость т.А направлена под углом к АС, а скорость т.В, лежащей между точками А и С, направлена вдоль стержня. Определить скорость точки С, если v_А = 6 м/c, v_В = 5 м/c, АВ = 10,5 м, ВС = 5 м.