Система координат

Прямолинейная координатная ось Ox (Oy,Oz) — прямая линия с выбранными положительным направлением (отмечается стрелкой), началом отсчета и единичным отрезком (масштабом).

Начало отсчёта — любая точка (обозначается буквой О), принадлежащая оси. Точка О делит ось на положительную (вдоль положительного направления) и отрицательную полуоси (рис.П3.1).

Единичный (масштабный) отрезок служит для измерения длин отрезков оси (расстояний между точками на оси) в единицах некоторой величины (например, длины).

Координата точки, принадлежащей оси Ox (обозначается x) — величина, равная:

а) длине L отрезка между началом отсчета и данной точкой:

x = L, (П3.1)

если точка находится на положительной полуоси (т.М на рис.П3.1а);

б) длине L отрезка между началом отсчета и данной точкой, умноженной на минус единицу:

x = L, (П3.2)

если точка находится на отрицательной полуоси (т.М на рис.П3.1б).

Прямоугольная (декартова) система координат на плоскости — система, состоящая из двух взаимно перпендикулярных прямолинейных координатных осей. Точка пересечения осей называется началом координат и обозначается буквой О.

На рис.П3.2 представлена система прямоугольных координат xOy. Ось Ox называется также осью абсцисс, ось Oy — осью ординат.

Проекция точки на ось — точка пересечения перпендикуляра, проведенного из данной точки к оси, с этой осью.

Координатойх (или y) точки, принадлежащей плоскости xOy (рис.П3.2) является координата х (или y) проекции данной точки на ось Ox (или Oy).

Расстояние d между двумя точками N₁(x₁,y₁) и N₂(x₂,y₂), расположенными на плоскости xOy:

, (П3.3)

где x₁ и y₁ — координаты точки N₁, x₂ и y₂ — координаты точки N₂ (рис.П3.2).

Прямоугольная (декартова) система координат в пространстве — система, состоящая из трех взаимно перпендикулярных координатных осей, пересекающихся в одной точке, которая является началом координат.

На рис.П3.3 представлена правая система координат в пространстве, в которой кратчайший поворот положительной полуоси Ox к положительной полуоси Oy виден со стороны положительной полуоси Oz происходящим против хода часовой стрелки. Ось Oz называется также осью аппликат.

Приложение 4

Скаляры. Функции и графики.

Скаляр — величина, определяемая одним числом.

Скаляр не зависит от направления в пространстве.

Две однородные скалярные физической величины равны, если при измерении их одной и той же единицей получаются одинаковые числа.

Приращение (изменение) некоторой величины A — разность между конечным (A_к) и начальным (A_н) значениями этой величины:

. (П4.1)

Убыль (разность) некоторой величины A — разность между начальным (A_н) и конечным (A_к) значениями этой величины:

. (П4.2)

Между убылью и приращением величины A выполняется соотношение:

. (П4.3)

Убыль ´A часто обозначают A.

Функция y = f(x) или y = y(x) — правило, по которому каждому числу x сопоставляется число y.

Числа x называются значением аргумента функции, числа y — значением функции (в точке x).

Область определения функции D — множество X чисел x.

Область значений функции R — множество Y чисел y.

График функции y(x) — множество точек на координатной плоскости xOy (Приложение 1) с координатами (x,y).

Графиком функции может быть некоторая линия.

Линейная функция  функция первой степени от аргумента:

y = ax + b, (П2.4)

где а (а  0) и b  некоторые константы.

Графиком линейной функции является прямая линия, тангенс угла наклона которой к оси Оx равен постоянной при аргументе функции:

tg = a. (П4.5)

На рис.П2.1 приведены графики этой функции при различных постоянных а и b.

Квадратичная функция  функция второй степени от аргумента:

, (П2.4)

где а (а  0), b и с  некоторые константы.

Графикомквадратичной функции является парабола. График этой функции при а  0 приведен на рис.П2.2а, при а  0  на рис.П2.2б.

ПРИЛОЖЕНИЕ 5

Векторы.

Вектор — величина, определяемая направлением в пространстве и модулем (абсолютной величиной).

Вектор изображается направленным отрезком прямой (рис.П5.1) и может обозначаться двумя буквами со стрелкой наверху, например (т.A — начало вектора, т.В — конец вектора), или буквой со стрелкой наверху, например ,либо одной буквой, напечатанной полужирным шрифтом, например a.

Модуль (абсолютная величина) вектора — длина вектора в выбранном масштабе. Обозначается: a или а.

Векторы подразделяются на свободные (начало вектора может находиться в любой точке пространства), скользящие (начало вектора может находиться в любой точке прямой, проходящей через начало и конец данного вектора) и связанные (начало вектора находится в определённой точке пространства).

Равенство свободных векторов

Два свободных вектора равны между собой, если их направления одинаковы и модули равны. На рис.П5.1 показаны два равных вектора а и b.

Коллинеарные векторы — векторы, лежащие на параллельных прямых.

Сложение векторов

Для сложения двух векторов a и b необходимо осуществить параллельный перенос вектора а (либо b) таким образом, чтобы конец одного вектора совпал с началом другого (рис.П5.2).

Сумма двух векторов a и b — вектор

, (П5.1)

начало которого совпадает с началом вектора a, конец — с концом

вектора b при условии, что начало вектора b совпадает с концом вектора a (правило треугольника — рис.П5.2).

Для вычисления модулей векторов и углов между ними в треугольнике может быть использованы теоремыкосинусов и синусов.

Например, стороны треугольника, показанного на рис.П5.2 связаны между собой следующими соотношениями:

по теореме косинусов

, (П5.2)

по теореме синусов

. (П5.3)

Сумма нескольких векторов

Для нахождения суммы n векторов можно параллельным переносом по очереди совместить начало последующего вектора с концом предыдущего вектора.

Суммой векторов a_i (i = 1,2,...,n) является вектор

, (П5.4)

начало которого совпадает с началом первого вектора, а конец — с концом последнего вектора.

На рис.П5.3 в качестве примера показаны четыре вектора, сумма которых равна вектору а.

Сложение векторов коммутативно:

, (П5.5)

и ассоциативно:

. (П5.6)

Умножение и деление вектора на скаляр

Произведением вектора a на скаляр n (действительное число) является вектор

b = na, (П5.7)

направление которого при положительном n (n>0) совпадает с направлением вектора а (рис.П5.4а,б), при отрицательном n (n<0) — противоположно вектору а (рис.П5.4,в,г), модуль которого

. (П5.8)

Из этого правила следует, что векторы а и а направлены в противоположные стороны, а их модули равны (рис.П5.4,г).

При n = 0 получается нулевой вектор.

Нулевой вектор 0 — вектор, начало и конец которого совпадают.

Модуль нулевого вектора равен нулю.

Деление вектора а на скаляр n можно представить как его умножение на скаляр, равный 1/n.

Вычитание векторов

Разностью векторов a и b является вектор

, (П5.9)

начало которого совпадает с концом вектора b, а конец — с концом вектора a, при условии, что начало вектора a совпадает с началом вектора b (рис.П5.5а).

Разность векторов а и b можно представить как сумму векторов а и b (рис.П5.5б):

. (П5.10)

Сумма и разность векторовa и b могут быть найдены также по правилу параллелограмма (рис.П5.6).

Проекция вектора на ось

Проекция вектора а на ось Оx (обозначается a_х) — величина, определяемая равенством:

, (П5.11)

где а — модуль вектора а,  — угол между вектором а и осью Oх (рис.П5.7,а и П5.7,б).

Проекция вектора а на ось Oх может быть определена также из из равенства:

, (П5.12)

где х_к и х_н — координаты конца и начала вектора а по оси Ох (рис.П5.7а и П5.7б).

Проекция вектора а на ось Ох может быть определена через длину L отрезка AB между проекциями конца (т.B) и начала (т.А) вектора a на ось Оx:

если угол между вектором а и положительной полуосью Oх острый (0 <   /2 — рис.П5.7,а), то:

а_х = L, (П5.13)

если угол между вектором а и положительной полуосью Ox тупой (/2<    — рис.П5.7,б), то:

а_х = L. (П5.14)

Если угол между вектором a и осью Ox прямой ( = /2), то:

а_х = 0. (П5.15)

Если вектор равен сумме векторов (равенство П5.4), его проекция на какую-либо ось (например, ось Оx) равна сумме проекций этих векторов на данную ось а_ix:

. (П5.16)

Радиус-вектор точки r — вектор, начало которого совпадает с началом координат, конец — с данной точкой (рис.П5.8).

П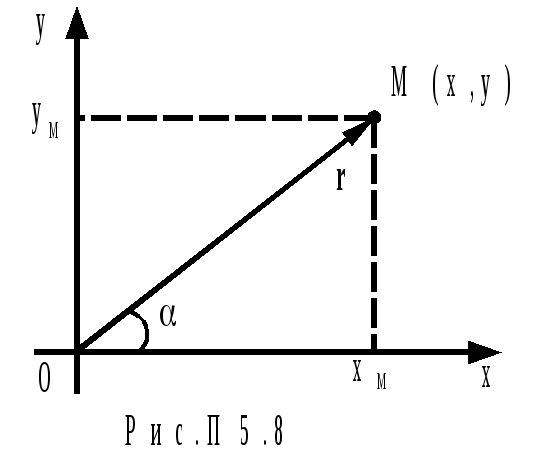роекции радиус-вектора некоторой точки на оси декартовых координат равны координатам этой точки:

(П5.17)

Единичный вектор а_ед — вектор, модуль которого равен единице:

 a_ед  = 1. (П5.18)

Единичный вектор может быть записан в виде выражения:

. (П5.19)

Орты — единичные векторы, направления которых совпадают с положительным направлением координатных осей.

Обозначение ортов по координатным осям: i — по оси Ox, j — по оси Oy (рис.П5.9).

Разложение вектора на составляющие — замена вектора несколькими векторами, сумма которых равна этому вектору.

Например, вектор а может быть разложен на две составляющие, параллельные координатным осям:

, (П5.20)

где a_x и a_y — составляющие вектора a, параллельные осям Ox и Oy соответственно (см. рис.П5.9)

Любой вектор может быть представлен в виде суммы векторов, выраженных через орты:

a = a_xi + a_yj, (П5.21)

где a_x и a_y — проекции вектора a на оси Ox и Oy, соответственно.

Вектор а (на плоскости) может быть задан двумя числами — либо модулем а и углом  к какой-либо оси (например, оси Ox), либо проекциями на оси а_x и а_y.

Они связаны между собой равенствами:

(П5.22)