Работа силы тяжести

A_тяж = mg(h_н – h_к) (14.19)

где h_н и h_к — начальная и конечная высоты (рис.14.7) материальной точки массой m, g — модуль ускорения свободного падения.

Р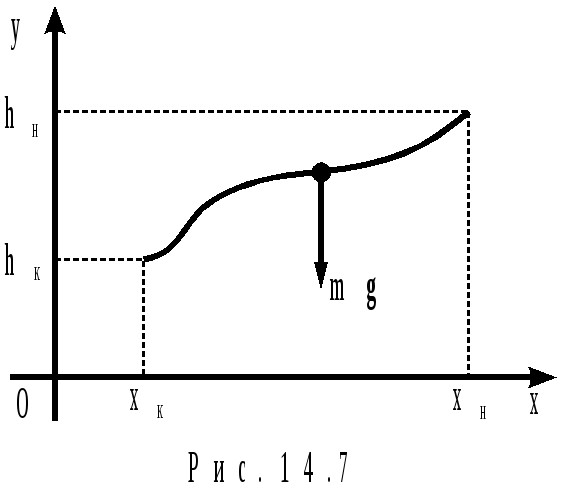абота силы тяжести A_тяж определяется начальным и конечным положениями материальной точки и не зависит от траектории между ними.

Она может быть положительной, отрицательной и равной нулю:

а) A_тяж > 0 — при спуске материальной точки,

б) A_тяж < 0 — при подъеме материальной точки,

в) A_тяж = 0 — при условии, что высота не изменяется, либо при замкнутой траектории материальной точки.

Работа силы трения при постоянных скорости м.т. (v = const ) и силы трения (F_тр = const) на промежутке времени t:

A_тр = (F_тр,v)t, (14.20)

Работа силы трения может быть положительной, отрицательной и равной нулю. Например:

а) работа силы трения, действующей на нижний брусок со стороны верхнего бруска (рис.14.8), A_тр.2,1 > 0, т.к. угол между силой, действующей на нижний брусок со стороны верхнего бруска F_тр.2,1 и скоростью v₂ нижнего бруска (относительно поверхности Земли) равен нулю;

б) A_тр.1,2 < 0 — угол между силой трения F_тр.1,2 и скоростью v₁ верхнего бруска равен 180 (см. рис.14.8);

в) А_тр = 0 — например, брусок находится на вращающемся горизонтальном диске (относительно диска брусок неподвижен).

Работа силы трения зависит от траектории между начальным и конечным положениями материальной точки.

§15. Механическая энергия

Кинетическая энергия материальной точки K — СФВ, равная половине произведения массы м.т. на квадрат модуля ее скорости:

(15.1)

Кинетическая энергия, обусловленная движением тела, зависит от системы отсчета и является неотрицательной величиной:

K 0. (15.2)

Единица кинетической энергии — джоуль: [К] = Дж.

Теорема о кинетической энергии — приращение кинетической энергии м.т. равно работе A_р равнодействующей силы:

K = A_р. (15.3)

Работа равнодействующей силы может быть найдена как сумма работ А_i всех сил F_i (i = 1,2,…n), приложенных к м.т.:

(15.4)

Модуль скорости материальной точки: при A_р > 0 — увеличивается; при A_р < 0 — уменьшается; при A_р = 0 — не изменяется.

Кинетическая энергия системы материальных точек K_с равна сумме кинетических энергий K_i всех n м.т., принадлежащих данной системе:

(15.5)

где m_i и v_i — масса и модуль скорости i-й м.т. данной системы.

Приращение кинетической энергии системы м.т. K_с равно сумме работ А_рi всех n равнодействующих сил, приложенных к i-м материальным точкам системы:

(15.6)

Поле сил — область пространства, в каждой точке которой на тело действуют силы.

Стационарное поле сил — поле, силы которого не изменяются с течением времени.

Однородное поле сил — поле, силы которого во всех его точках одинаковы.

Центральное поле сил — поле, направления действия всех сил которого проходят через одну точку, называемую центром поля, а модуль сил зависит только от расстояния до этого центра.

Неконсервативные силы (нкс.сл) — силы, работа которых зависит от траектории между начальным и конечным положениями тела.

Пример неконсервативных сил — силы трения. Работа сил трения по замкнутой траектории в общем случае не равна нулю.

Консервативные силы (кс.сл) — силы, работа которых определяется начальным и конечным положениями м.т. и не зависит от траектории между ними. При замкнутой траектории работа консервативных сил равна нулю. Поле консервативных сил называется потенциальным.

Пример консервативных сил — силы тяжести и упругости.

Потенциальная энергия П — СФВ, являющаяся функцией взаимного расположения частей системы (тела).

Единица потенциальной энергии — джоуль: [П] = Дж.

Теорема о потенциальной энергии

Убыль потенциальной энергии системы материальных точек равна работе консервативных сил:

–П_с = П_н – П_к = A_кс.сл (15.7)

Потенциальная энергия определяется с точностью до постоянной величины и может быть положительной, отрицательной или равной нулю.

Потенциальная энергия материальной точки П в какой-либо точке силового поля — СФВ, равная работе консервативных сил при перемещении м.т. из данной точки поля в точку, потенциальная энергия в которой принята равной нулю:

П = A_кс.сл. (15.8)

Потенциальная энергия упругодеформированной пружины

(15.9)

где х — смещение незакрепленного конца пружины; к — жесткость пружины, С — произвольная постоянная (выбирается из условия удобства решения задачи).

Графики П(х) при различных постоянных: а) С > 0, б) С = 0, в) С < 0  параболы (рис.15.1).

При условии П (0) = 0 постоянная С = 0 и

(15.10)