Для решения некоторых задач можно считать, что

p_с = const, (13.24)

если приращением импульса системы, по сравнению с начальным значением, можно пренебречь:

p_с  p_нс, (13.25)

вследствие малых значений равнодействующей внешних сил и/или промежутка времени действия внешних тел, приводящих к малой величине импульса равнодействующей внешних сил.

§14. Работа и мощность

Работа постоянной силы при прямолинейном движении А — СФВ, равная скалярному произведению постоянной силы F на перемещение м.т. r, на котором действует эта сила:

A = (F,r) = F|r|cos, (14.1)

где сила F = const на r,  — угол между перемещением r и силой F (рис.14.1).

Единица работы — джоуль: [A] = Дж = кгм²/с².

Работа силы может быть положительной, равной нулю и отрицательной:

а) А > 0 при 0   < /2;

б) А = 0 при  = /2;

в) А < 0 при /2 <   .

Работа постоянной силы может быть выражена также через произведение:

а) проекции силы на ось Ol, совпадающей по направлению с перемещением l, и модуля этого перемещения:

A = F_ll, (14.2)

б) проекции перемещения на ось OF, совпадающей по направлению с силой F, и модуля этой силы:

A = l_FF, (14.3)

в) проекций силы и перемещения на координатные оси (при движении м.т. в плоскости хОу):

A = F_хх + F_yy. (14.4)

В частности, при прямолинейном движении материальной точки вдоль оси Ох работа постоянной силы

A = F_xx. (14.5)

Работа постоянной силы при прямолинейном движении вдоль оси Ох в системе координат F_xOx равна площади (в единицах работы) прямоугольника, ограниченного графиком F_cx(х), осью Ох от начальной до конечной координаты м.т. и отрезками прямых х = х_н и х = х_к (рис.14.2).

Работа переменной силы при произвольном движении материальной точки — СФВ, равная пределу суммы скалярных произведений силы F_i (рис.14.3) на перемещение м.т. r_i, на котором действует эта сила, при бесконечном уменьшении перемещений r_i:

(14.6)

Работа переменной силы при прямолинейном движении м.т. вдоль оси Ох

(14.7)

Работа такой силы в системе координатF_xOx равна площади (в единицах работы) криволинейной трапеции (рис.14.4), ограниченной графиком F_x(х), осью Ох и отрезками прямых х = х_н и х = х_к.

Средняя мощность <Р> — СФВ, равная отношению работы к промежутку времени t, за который совершена эта работа:

(14.8)

Мощность (мгновенная) Р — СФВ, равная пределу отношения элементарной работы A к промежутку времени t, за который совершена эта работа, при бесконечном уменьшении промежутка времени:

(14.9)

Единица мощности — ватт: [Р] = Вт = кгм²/с³.

Мощность P может быть выражена через скорость v и силу F, приложенную к материальной точке. Она равна их скалярному произведению:

P = (F,v) = Fvcos , (14.10)

где  — угол между силой F и скоростью v материальной точки.

Мощность также может быть выражена через F_v — проекцию силы на ось Ov, совпадающую по направлению со скоростью v, или через v_F — проекцию скорости на ось OF, совпадающую по направлению с силой F:

P = F_vv = Fv_F , (14.11)

либо через проекции силы и скорости на координатные оси (при движении м.т. в плоскости хОу):

P = F_хv_х + F_уv_у. (14.12)

Работа упругой силы может быть определена из следующих равенств:

(14.13)

(14.14)

(14.15)

где х_н и x_к — начальное и конечное смещения незакрепленного конца пружины, к которому приложена внешняя сила F_внеш (рис.14.5а), к — жесткость пружины.

Работа упругой силы может быть положительной, отрицательной и равной нулю:

а) A_упр > 0 — при уменьшении удлинения (укорочения) пружины;

б) A_упр < 0 — при увеличении длины пружины при растяжении или уменьшении длины при сжатии пружины;

в) A_упр = 0 — при угле между силой упругости и скоростью м.т., равном 90 (например, при движении м.т. по дуге АВ окружности, представленной на рис.14.5, б), или при замкнутой траектории.

Р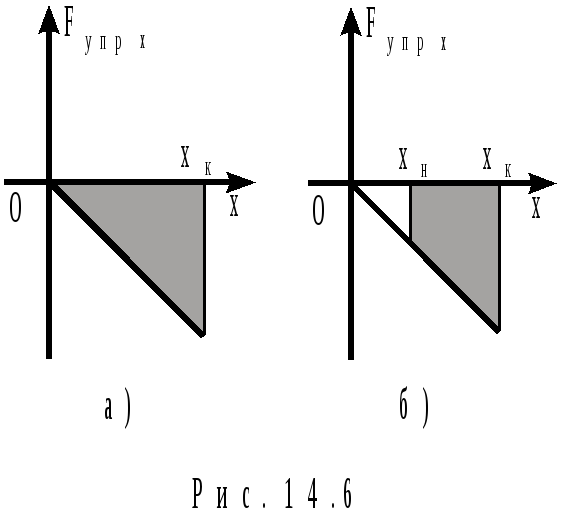абота упругой силы в системе координатF_упр.хOx равна площади (в единицах работы) прямоугольного треугольника при растяжении или сжатии пружины (на рис.14.6,а – при растяжении) из ненагруженного (х_н = 0) состояния или площади трапеции при растяжении или сжатии пружины из нагруженного (х_н  0) состояния (на рис.14.6,б – при растяжении), ограниченных соответствующим графиком F_упр.x(х), осью Ох от начальной до конечной координаты незакрепленного конца пружины и отрезками прямых х = х_н (в первом случае х_н = 0) и х = х_к.

Работа упругой силы определяется только начальным и конечным положениями м.т. и не зависит от траектории между этими точками.