
- •1. Скалярное поле. Поверхности и линии уровня. Производная по направлению и градиент
- •Производная по направлению
- •Градиент скалярного поля
- •2. Поток векторного поля
- •1) Найти поток векторного поля через поверхность сферы
- •3. Криволинейные координаты. Теорема гаусса-остроградского. Дивергенция векторного поля
- •Теорема Гаусса - Остроградского
- •4. Линейный интеграл в векторном поле. Циркуляция векторного поля и ротор
- •Подставив всё это в интеграл, получим:
- •5. Теорема стокса. Независимость линейного интеграла от пути интегрирования. Потенциальное векторное поле
- •6. Оператор гамильтона “набла”. Дифференциальные операции первого и второго порядка
- •7. Заключение
- •Литература
4. Линейный интеграл в векторном поле. Циркуляция векторного поля и ротор
Пусть дано векторное поле
![]()
и
кривая
![]() ,
на которой указано положительное
направление. (Функции
,
на которой указано положительное
направление. (Функции![]() непрерывные, кривая кусочно-гладкая.)
Если
непрерывные, кривая кусочно-гладкая.)
Если![]()
силовое поле, то работа по перемещению
единичной массы на отрезке кривой
силовое поле, то работа по перемещению
единичной массы на отрезке кривой
![]()
будет равна
![]()
Работу,
произведенную силой
![]() при перемещении единичной массы по пути
при перемещении единичной массы по пути![]() ,
можно представить криволинейным
интегралом второго рода
,
можно представить криволинейным
интегралом второго рода
![]() . (4.1)
. (4.1)
Если кривая L задана системой уравнений
![]() ,
,
то интеграл (4.1) вычисляется по формуле
![]()
![]() ,
,
а в случае параметрического задания кривой:
![]() ,
,
формула принимает вид:
![]() .
.
Пример 4.1. Вычислить линейный интеграл в векторном поле
![]()
на
отрезке прямой АВ.
![]() .
.
Решение.
![]() .
.
Каноническое уравнение прямой АВ
![]() ,
,
откуда
![]() .
.
Интеграл будет равен:
![]() .
.
Пример 4.2. Вычислить линейный интеграл в векторном поле
![]()
вдоль
линии
![]()
Решение.
Здесь ![]() ;
;
![]()
![]()
Пример 4.3. Вычислить линейный интеграл в векторном поле
![]()
вдоль полуокружности
![]() .
.
Решение.
![]()
где
![]() ,
,
следовательно,
![]()
![]()
Пример 4.4
Вычислить линейный интеграл в векторном поле
![]()
вдоль
винтовой линии
![]() ,
задаваемой уравнениями,
,
задаваемой уравнениями,
![]() .
.
Решение.
![]() ,
,
следовательно,
![]()

![]() .
.
Решить самостоятельно
Вычислить линейный интеграл в векторном поле
![]()
вдоль параболы
![]() от точки (0,0) до точки (1,1).
от точки (0,0) до точки (1,1).
2) Вычислить линейный интеграл в векторном поле
![]() :
:
а)
вдоль параболы
![]() от точки (-1,1) до точки (1,1);
от точки (-1,1) до точки (1,1);
б) вдоль прямой, соединяющей эти же точки.
Вычислить линейный интеграл в векторном поле
![]()
вдоль прямой, соединяющей точки (1,1,1) и (2,2,2).
![]()
![]() Циркуляцией
векторного поля
называется линейный интеграл второго
рода, взятый по замкнутой ориентированной
кривой L:
Циркуляцией
векторного поля
называется линейный интеграл второго
рода, взятый по замкнутой ориентированной
кривой L:
![]() ,
(4.2)
,
(4.2)
где
![]()
векторное поле, а
![]()
элементарный отрезок кривой L.
Направление обхода замкнутой кривой L считается положительным, если для наблюдателя, движущегося в этом направлении, область, ограниченная кривой, остаётся слева.
Пример 4.5. Вычислить циркуляцию векторного поля
![]()
вдоль эллипса
![]() .
.
Решение.
![]() .
.
Параметричекские уравнения эллипса имеют вид
![]()
![]()
![]()
откуда
![]() ,
,
![]() .
.
Подставив всё это в интеграл, получим:
![]() ,
так как
,
так как
![]() Аналогично
Аналогично
![]() .
.
Пример 4.6. Вычислить циркуляцию в векторном поле
![]() ,
,
если L линия пересечения цилиндра
![]()
и плоскости
![]() .
.
Решение.
![]() .
.
Линия
![]() есть эллипс, параметрические уравнения
которого имеют вид:
есть эллипс, параметрические уравнения
которого имеют вид:
![]()
![]()
![]()
![]() ,
,
откуда
![]()
![]()
![]()
Подставив всё в интеграл, получим:
![]()
![]()
![]() .
.
Решить самостоятельно
4)
Вычислить циркуляцию векторного поля![]() вдоль замкнутой кривой
вдоль замкнутой кривой![]() .
.
![]()
![]() :
:![]()
![]()
Ротор
векторного поля
это вектор, обозначаемый символом
![]() .
.
Пусть
![]()
векторное поле, причём функции P, Q и R непрерывны вместе с производными первого порядка по всем переменным. Тогда
![]() ,
,
или, в символической форме:
 .
.
Пример 4.7.
Пусть
![]() скалярная
функция,
скалярная
функция,![]() векторная
функция. Показать, что
векторная
функция. Показать, что![]() .
.
Решение.
![]()

![]()
![]()

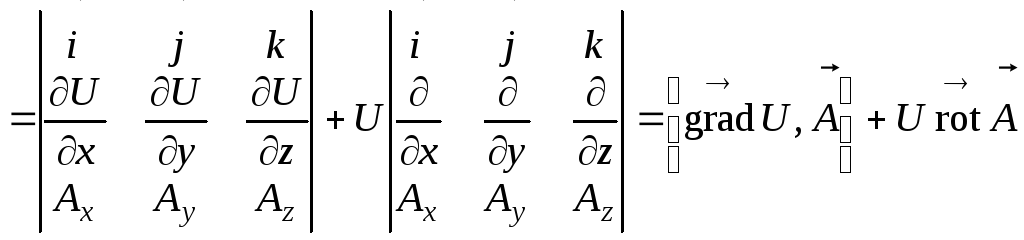 .
.
Пример 4.8. Пусть
![]()
![]()
![]() постоянный
вектор. Показать, что
постоянный
вектор. Показать, что
![]() .
.
Решение.
![]()
(Обозначаем
здесь и далее![]() .)
.)

![]()
![]()
 .
.
Здесь, например,
 .
.
Решить самостоятельно
5) Показать,
что если
![]() и
и![]() постоянные векторы, а
постоянные векторы, а![]() то
то![]() .
.
6) Показать,
что
![]() .
.
где
![]() постоянный вектор,
постоянный вектор,![]()
Ответы.![]()
5. Теорема стокса. Независимость линейного интеграла от пути интегрирования. Потенциальное векторное поле
Теорема Стокса.
Пусть
![]() ограниченная,
полная, кусочно-гладкая, двусторонняя
поверхность с кусочно-гладкой границей
ограниченная,
полная, кусочно-гладкая, двусторонняя
поверхность с кусочно-гладкой границей![]() .Окрестностью поверхности
.Окрестностью поверхности![]() будем называть любое открытое множество
будем называть любое открытое множество![]() ,
содержащее
,
содержащее![]() .
.
Теорема.
Пусть в некоторой окрестности
поверхности
![]() функции
функции![]() непрерывны и имеют непрерывные частные
производные первого порядка. Тогда
имеет место следующее соотношение:
непрерывны и имеют непрерывные частные
производные первого порядка. Тогда
имеет место следующее соотношение:
![]()
![]() , (5.1)
, (5.1)

Рис. 9
называемое
формулой Стокса. При этом,
стоящий в правой части интеграл
вычисляется по замкнутому контуру
![]() ,
являющемуся границей поверхности
,
являющемуся границей поверхности![]() ,
на котором указано такое направление
обхода, при котором (с учётом выбора
стороны поверхности) поверхность
,
на котором указано такое направление
обхода, при котором (с учётом выбора
стороны поверхности) поверхность![]() остаётся слева.
остаётся слева.
Будем
считать, что
![]() однозначно проецируется на координатные
плоскости в трёхмерном пространстве,
причём, на плоскость
однозначно проецируется на координатные
плоскости в трёхмерном пространстве,
причём, на плоскость![]() в область
в область![]() и является графиком некоторой функции
и является графиком некоторой функции![]() ,
определенной в
,
определенной в![]() ,
(Рис. 9).
,
(Рис. 9).
Докажем теорему.
Касательная
плоскость к поверхности
![]() имеет уравнение:
имеет уравнение:
![]() ,
,
где
![]() произвольная точка на поверхности
произвольная точка на поверхности![]() .
.
Нормаль в точке касания есть вектор
![]() ,
,
компоненты которого определены в той же точке. Единичный вектор нормали равен
 ,
,
следовательно,

 .
.
Очевидно, теорема будет доказана, если будут доказаны равенства:
![]() ;
;
![]() ; (5.2)
; (5.2)
![]() .
.
Поскольку эти соотношения доказываются однотипно, остановимся на доказательстве только первого из них.
Проекции
элементарной площадки
![]() на координатные плоскости равны,
соответственно:
на координатные плоскости равны,
соответственно:
![]() ;
;
![]() .
.
Подставив последнее соотношение в поверхностный интеграл, получим
![]() .
.
Так
как на поверхности
![]()
![]() ,
,
то, используя правило дифференцирования сложной функции, получим
![]() .
.
Подставим
это в поверхностный интеграл и вычислим
его, переходя к двойному интегралу по
области
![]() на плоскости
на плоскости![]() ,
в которую проецируется поверхность
,
в которую проецируется поверхность![]() .
.
 .
.
Здесь
![]() и
и![]() уравнения двух
ветвей замкнутого контура
уравнения двух
ветвей замкнутого контура![]() ,
в который проецируется граница
,
в который проецируется граница![]() поверхности
поверхности![]() .
Поменяв местами пределы в последнем
интеграле, мы замкнём обход контура
.
Поменяв местами пределы в последнем
интеграле, мы замкнём обход контура![]() ,
однако направление обхода – отрицательное
(так как область
,
однако направление обхода – отрицательное
(так как область![]() при обходе остаётся справа) и получим:
при обходе остаётся справа) и получим:
 .
.
Изменив
направление обхода контура
![]() ,
мы избавимся от знака минус перед
интегралами, а учитывая тот факт, что
значение функции
,
мы избавимся от знака минус перед
интегралами, а учитывая тот факт, что
значение функции![]() в точке
в точке![]() кривой
кривой![]() совпадает со значением функции
совпадает со значением функции![]() в точке
в точке![]() кривой
кривой![]() ,
в которую проецируется точка
,
в которую проецируется точка![]() ,
получим:
,
получим:
![]() .
.
Окончательный результат:
![]() .
.
Первое из трёх равенств (5.2) доказано. Второе и третье доказываются аналогично. Теорема доказана.
Теорема Стокса может быть сформулирована более компактно, а формула Стокса записана в «свёрнутом виде». При этом ограничения, оговоренные в формулировке теоремы Стокса, сохраняются в полном объёме.
Циркуляция
вектора
![]() по замкнутому контуру L равна потоку
ротора этого вектора через любую
поверхность S , натянутую на контур L,
ограничивающий эту поверхность:
по замкнутому контуру L равна потоку
ротора этого вектора через любую
поверхность S , натянутую на контур L,
ограничивающий эту поверхность:
![]() , (5.3)
, (5.3)
где
![]()
![]() ,
,
![]() ,
,
![]() орт
нормали к поверхности S,
орт
нормали к поверхности S,
![]() проекция
вектора ротора на нормаль к поверхности
S.
проекция
вектора ротора на нормаль к поверхности
S.
 .
.
Ориентация
нормали
![]() и выбор стороны поверхностиS
согласованы так, что обход контура L
виден из конца вектора нормали
и выбор стороны поверхностиS
согласованы так, что обход контура L
виден из конца вектора нормали
![]() соверша-ющимся против часовой стрелки:
соверша-ющимся против часовой стрелки:
Пример 5.1. Вычислить циркуляцию вектора
![]()
по
контуру L:
![]()
![]()
![]()
![]() ,
,
непосредственно, b) по формуле Стокса. (Рис. 10).
Решение.
а)
![]() ,
,
![]()
![]()
![]()

Рис. 10
Для вычислений по теореме Стокса в качестве поверхности,
натянутой
на контур L, выберем плоскость
![]() Нормаль в этом случае
вектор
Нормаль в этом случае
вектор
![]() :
:
 ,
,
![]() ,
,

![]()
![]() .
.
Решить самостоятельно
1) Найти циркуляцию вектора
![]()
по контуру, образованному пересечением плоскости
![]()
с координатными плоскостями;
найти циркуляцию векторного поля.
![]()
по контуру
![]()
![]()
![]()
Теорема.Для того, чтобы линейный интеграл
![]()
не зависел от формы пути интегрирования L, необходимо и достаточно, чтобы векторное поле
![]()
было
безвихревым, т.е.
![]() в каждой точке области G, в которой задано
векторное поле.
в каждой точке области G, в которой задано
векторное поле.
Здесь
предполагается, что компоненты вектора
![]() :
:![]() непрерывны вместе с частными производными
первого порядка, а сама областьG односвязная.
непрерывны вместе с частными производными
первого порядка, а сама областьG односвязная.
Определение.Область G трёхмерного пространства называется односвязной, если на любой замкнутый контур, принадлежащий области, можно натянуть поверхность, целиком лежащую в области G.
Например, трёхмерное пространство, внутренность сферы являются односвязными областями. Внутренность тора, пространство с «выколотой» точкой или выброшенной прямой, не являются односвяз-ными областями.
При
выполнении условий теоремы циркуляция
вектора
![]() по любому замкнутому контуру
по любому замкнутому контуру![]() ,
принадлежащему областиG, равна
нулю:
,
принадлежащему областиG, равна
нулю:
![]() .
.
В случае плоского векторного поля
![]()
имеем
 .
.
Следовательно, для того, чтобы в плоском поле, определённом в односвязной области G, линейный интеграл
![]()
![]()
не зависел от формы пути интегрирования, необходимо и достаточно, чтобы выполнялось соотношение
![]() .
.
Если в области Dс границейLзадано плоское векторное поле
![]() ,
,
то справедлива формула Грина
![]() . (5.4)
. (5.4)
Теорема Грина представляет собой частный случай теоремы Стокса.
Пример 5.2.
С помощью формулы Грина вычислить линейный интеграл
![]()
в векторном поле
![]() ,
,
где
![]() верхняя полуокружность
верхняя полуокружность![]() ,
причём начало пути интегрирования в
точке
,
причём начало пути интегрирования в
точке![]() ,
а конецв точке
,
а конецв точке![]() .
(Рис. 11).
.
(Рис. 11).
Решение.
Замкнём
контур интегрирования, прибавив к дуге
![]() отрезок
отрезок![]() ,
который проходится от точки
,
который проходится от точки![]() до точки
до точки![]() по оси
по оси![]() ,
имея в виду, что
,
имея в виду, что
 ,
,
так
как на оси
![]()
![]() и
и![]() .
Пусть
.
Пусть![]() .
Тогда
.
Тогда
![]() ,
,

Рис. 11
где
![]()
![]()
![]()
откуда следует
![]() ,
,
где
Sверхняя
половина круга![]()
Последний интеграл вычислим в полярных координатах:
![]()
![]() .
.
Подставив эти соотношения в уравнение окружности, получим:
![]() откуда
откуда
![]() .
.
Конечный результат:
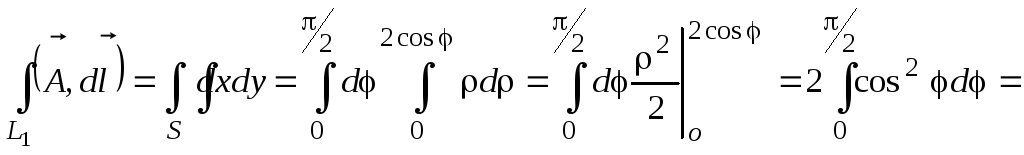

Решить самостоятельно
Применяя формулу Грина, вычислить циркуляцию следующих векторных полей по заданным контурам:
3)
![]()
![]()
![]()
![]()
![]() ;
;
4).
![]()
![]()
![]()
![]() ;
;
5)
![]()
![]()
![]() ;
;
6)
![]()
![]() :
:![]()
![]()
![]()
Определение.
Векторное поле
![]()
заданное
в области
![]() трёхмерного пространства, называется
потенциальным, если существует такая
скалярная функция
трёхмерного пространства, называется
потенциальным, если существует такая
скалярная функция![]() что во всех точках области
что во всех точках области
![]() выполняется равенство
выполняется равенство
![]() ,
,
или, что равносильно,
![]()
![]()
![]() .
.
Функция
![]() ,
удовлетворяющая этим условиям, называется
потенциалом векторного поля
,
удовлетворяющая этим условиям, называется
потенциалом векторного поля![]() .
Потенциал поля определяется с точностью
до постоянной.
.
Потенциал поля определяется с точностью
до постоянной.
Теорема.Для того, чтобы векторное поле
![]() ,
заданное в односвязной области
,
заданное в односвязной области![]() было потенциальным, необходимо и
достаточно, чтобы в каждой точке области
было потенциальным, необходимо и
достаточно, чтобы в каждой точке области![]() выполнялось условие:
выполнялось условие:
![]()
Потенциал векторного поля
![]()
определяется формулой
 ,
,
где
![]() фиксированная
точка, а
фиксированная
точка, а![]() произвольная точка.
произвольная точка.
Пример 5.3
Показать, что поле
![]()
является потенциальным и найти его потенциал.
Решение.
![]()
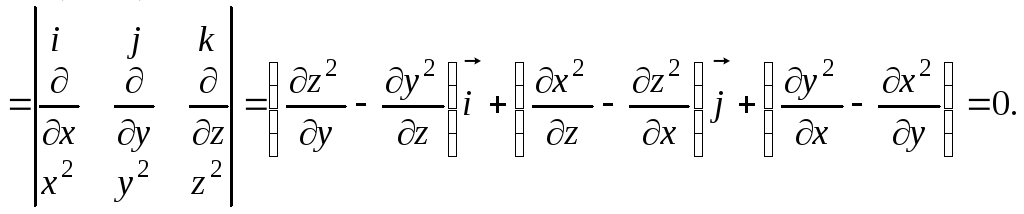
Следовательно, поле потенциально. Потенциал поля:
 .
.
Теорема.Линейный интеграл в потенциальном
поле
![]() равен разности значений потенциала
поля
равен разности значений потенциала
поля![]() в конечной и начальной точках пути
интегрирования:
в конечной и начальной точках пути
интегрирования:
 . (5.5)
. (5.5)
Пример 5.4.Вычислить линейный интеграл в поле вектора
![]()
вдоль
отрезка прямой от точки
![]() до точки
до точки![]()
Решение.
 ,
,
следовательно, векторное поле является потенциальным:


Результат
не зависит от того, какая кривая соединяет
точки
![]() и
и![]() Это
позволяет выбрать путь, соединяющий
точки
Это
позволяет выбрать путь, соединяющий
точки![]() и
и![]() в виде ломаной, состоящей из отрезков,
параллельных осям координат, что приводит
к упрощению интеграла для нахождения
потенциала:
в виде ломаной, состоящей из отрезков,
параллельных осям координат, что приводит
к упрощению интеграла для нахождения
потенциала:
![]()
![]()


Пример 5.5.
Доказать, что векторное поле
![]()
является потенциальным и найти его потенциал.
Решение.
![]()

т.е. поле потенциальное.
1-й способ решения:
В
качестве начальной точки пути
интегрирования выберем
![]() ,
а линию
,
а линию![]() ,
соединяющую её с конечной точкой
,
соединяющую её с конечной точкой![]() ,
представим ломаной, состоящей из
отрезков, параллельных координатным
осям. (Рис. 12).
,
представим ломаной, состоящей из
отрезков, параллельных координатным
осям. (Рис. 12).
Получим:
![]()

Рис. 12
2-й способ.
Полный
дифференциал функции
![]()
![]()
В потенциальном поле
![]()
![]()
![]()
Подставив эти значения в полный дифференциал, получим:
![]()
![]()
откуда следует, что
![]()
Решить самостоятельно
В следующих задачах установить потенциальность векторных полей
![]() и
найти их потенциалы
и
найти их потенциалы
![]()
7)
![]() ;
;
8)
![]() ;
;
9)
![]()
Ответы.
 2)
0; 3) -1; 4)
2)
0; 3) -1; 4)
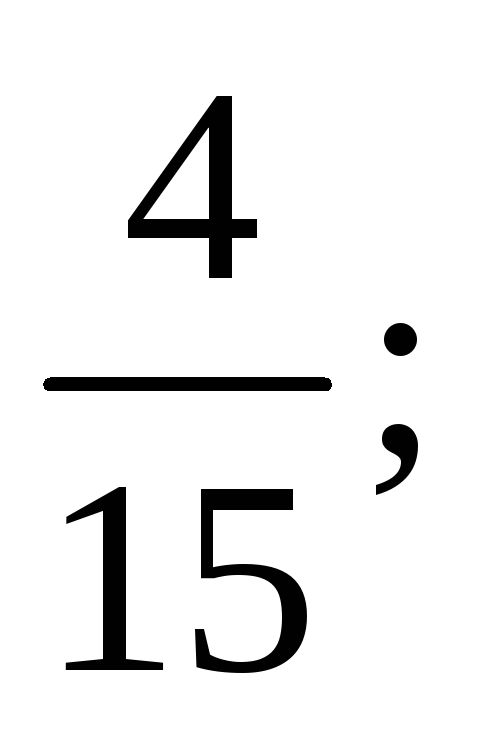 5) 0; 6)
5) 0; 6) 7)
7) 8)
8)
 .
.
