Kollokvium2

Вопросы к коллоквиуму-2

2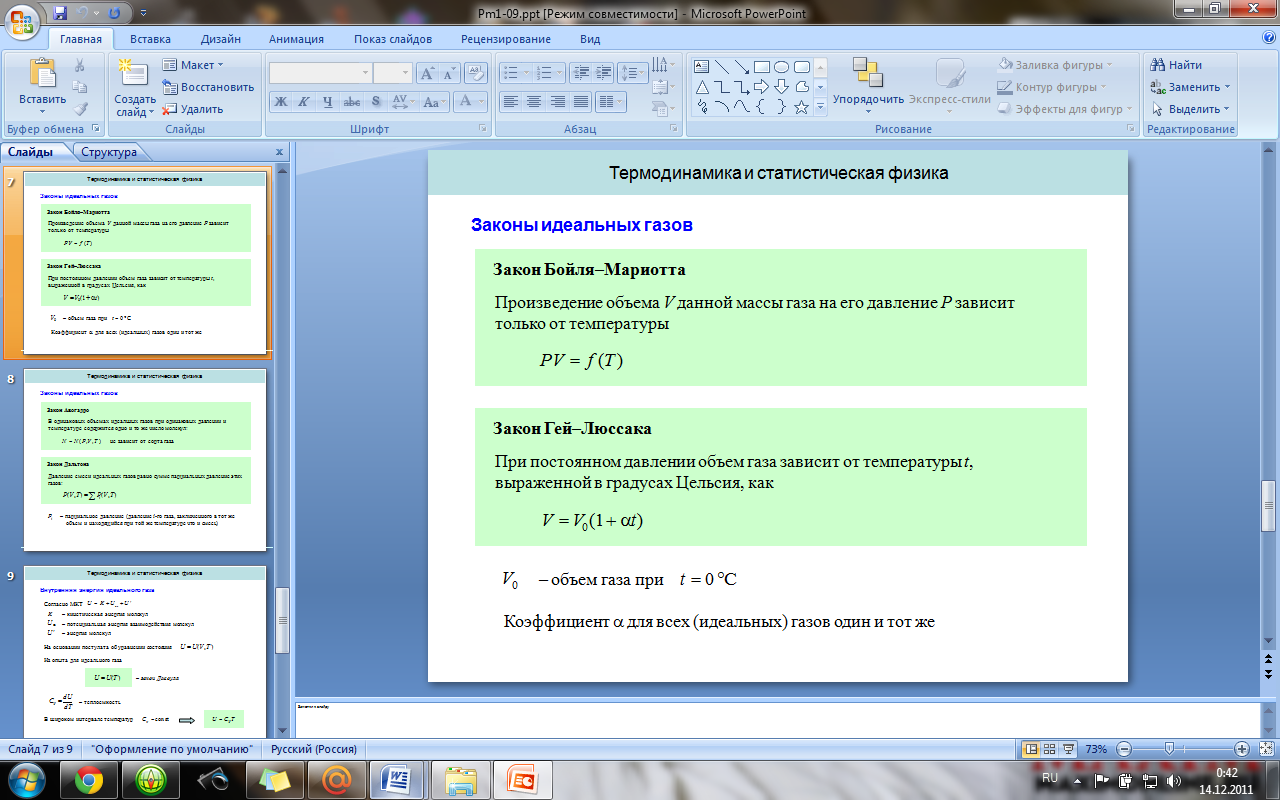. Законы идеальных газов: Бойля-Мариотта, Гей-Люссака, Авогадро, Дальтона.

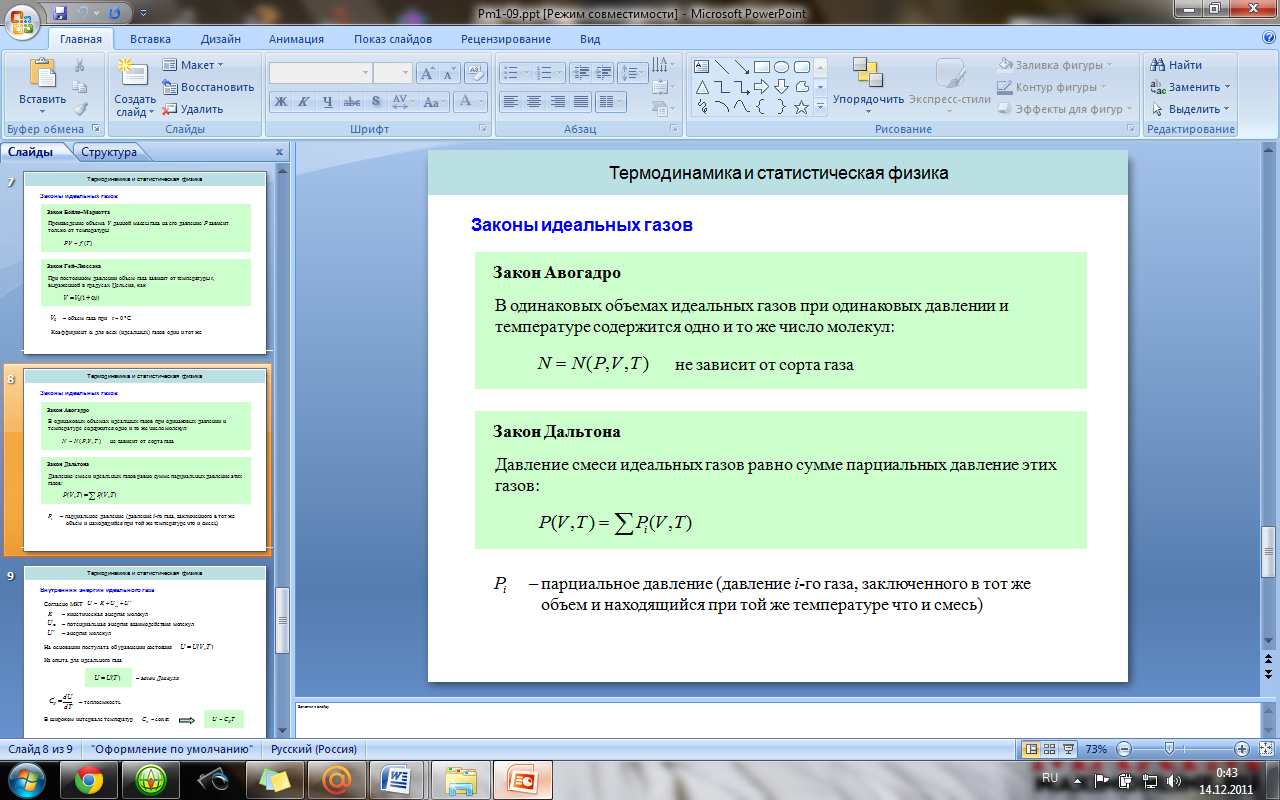
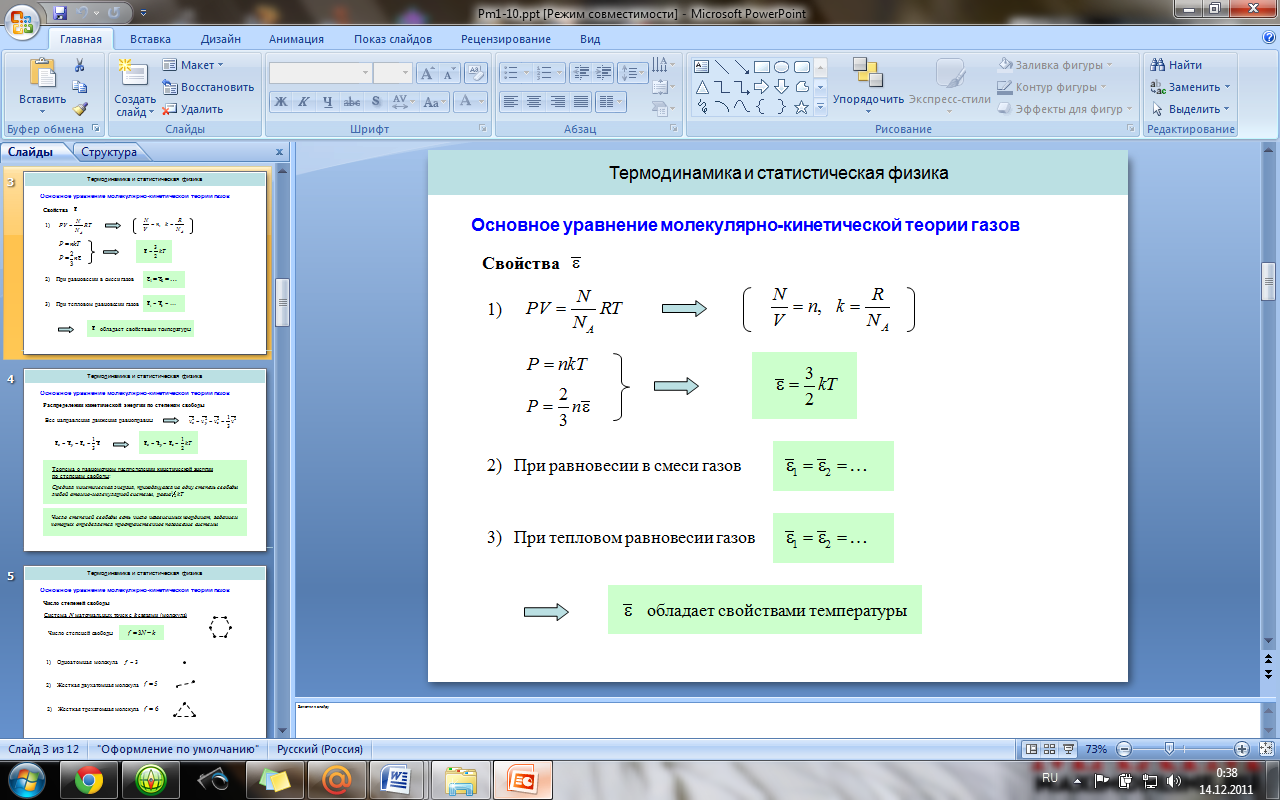
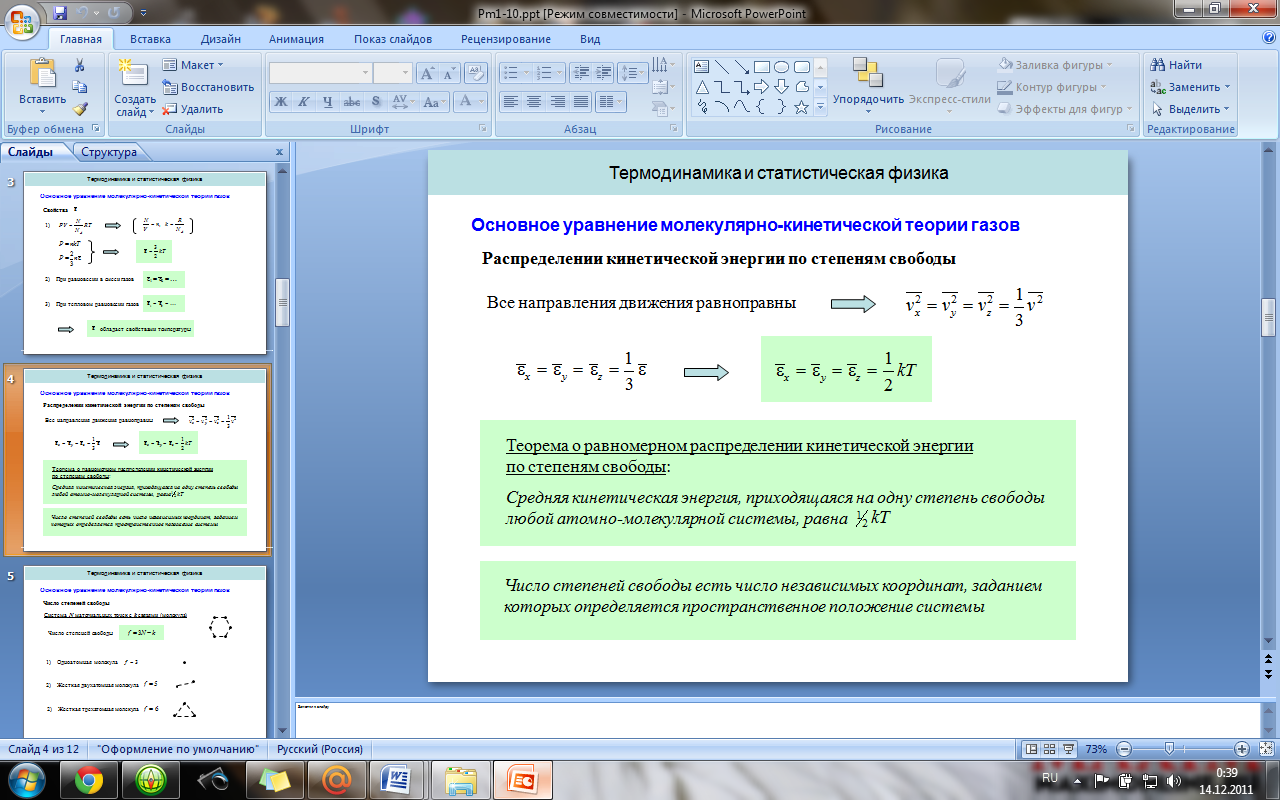
4. Основное уравнение молекулярно-кинетической теории. Средняя кинетическая энергия молекул, молекулярно-кинетический смысл температуры.

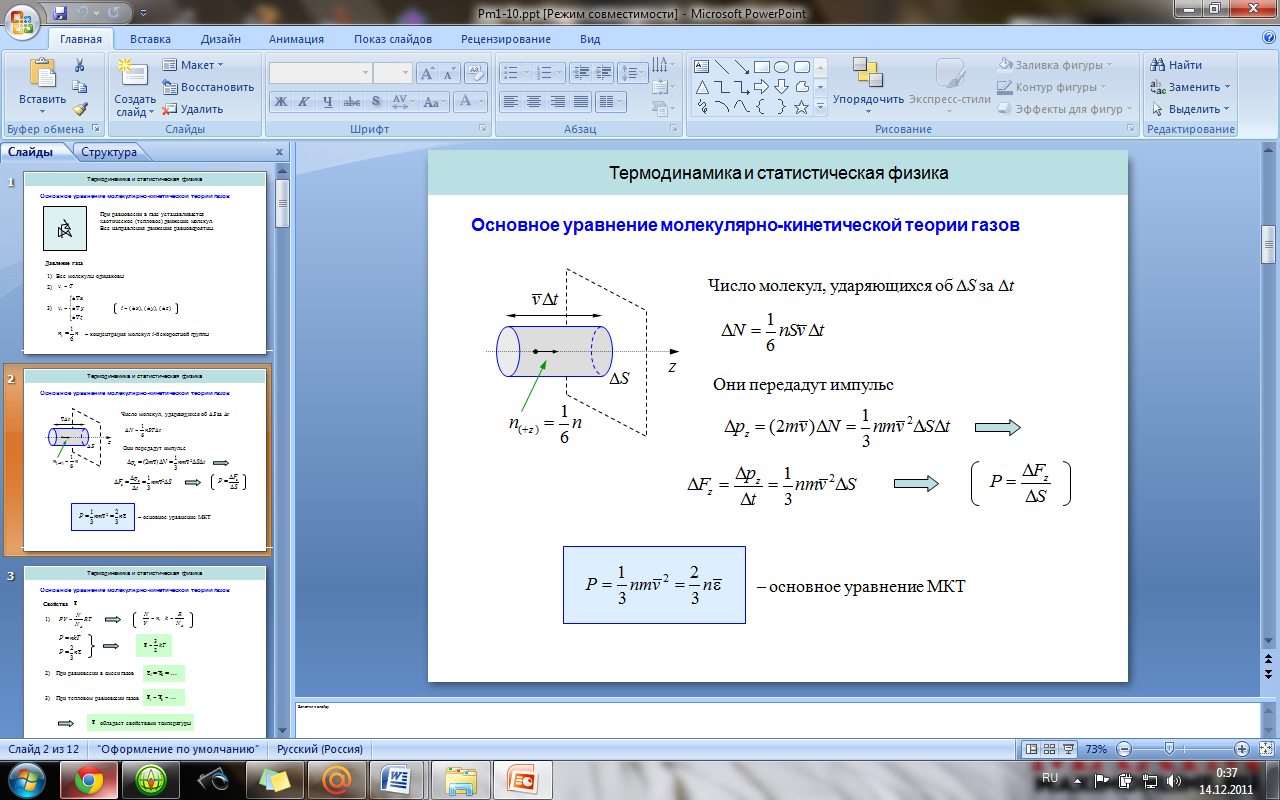
6. Идеальный газ в поле силы тяжести. Барометрическая формула. Распределение Больцмана.

Д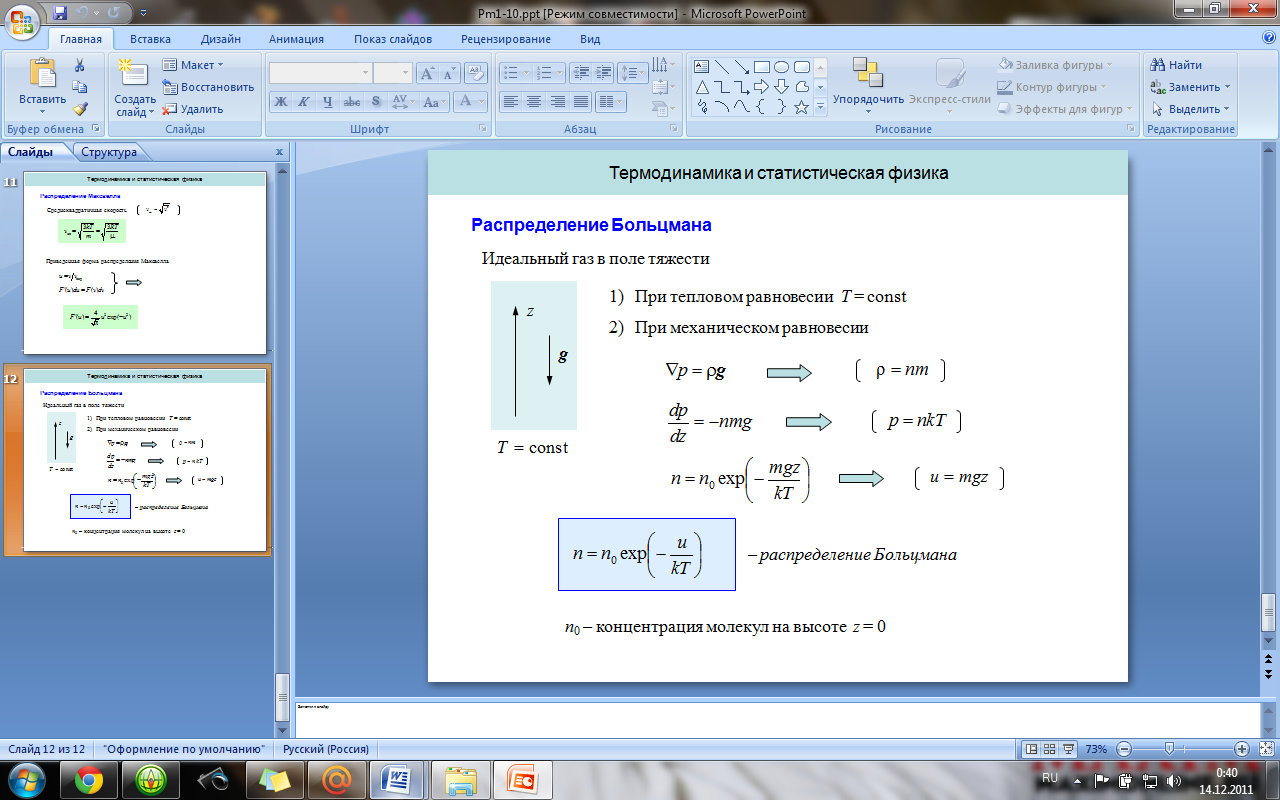ля идеального газа, имеющего постоянную температуру T и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения g одинаково), барометрическая формула имеет следующий вид:

где p — давление газа в слое, расположенном на высоте h, p₀ — давление на нулевом уровне (h = h₀), M — молярная масса газа, R — газовая постоянная, T — абсолютная температура.

Барометрическая формула позволяет найти атмосферное давление в зависимости от высоты или измерив давление найти высоту. Идеальный газ — модель, в которой пренебрегают потенциальной энергией взаимодействия молекул. Между молекулами не действуют силы притяжения, соударения частиц между абсолютно упругие, время взаимодействия между молекулами пренебрежимо мало.

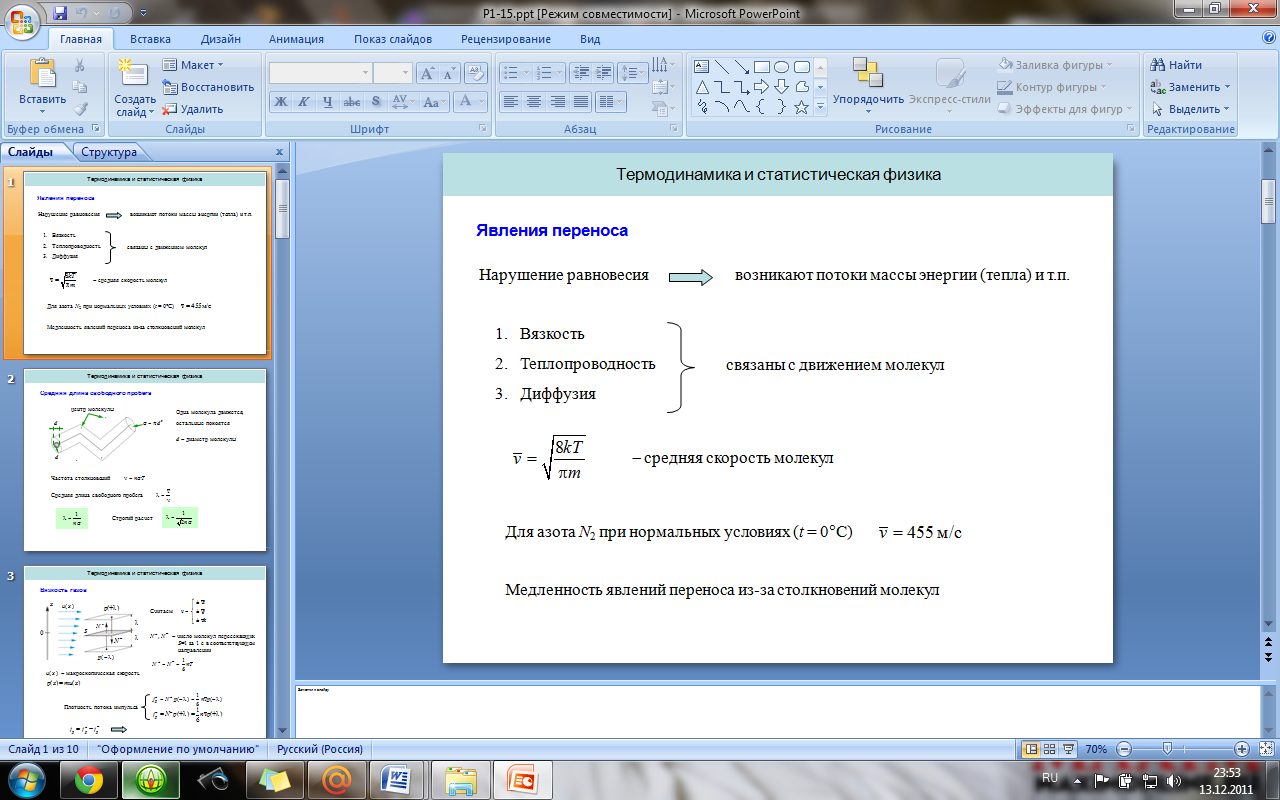
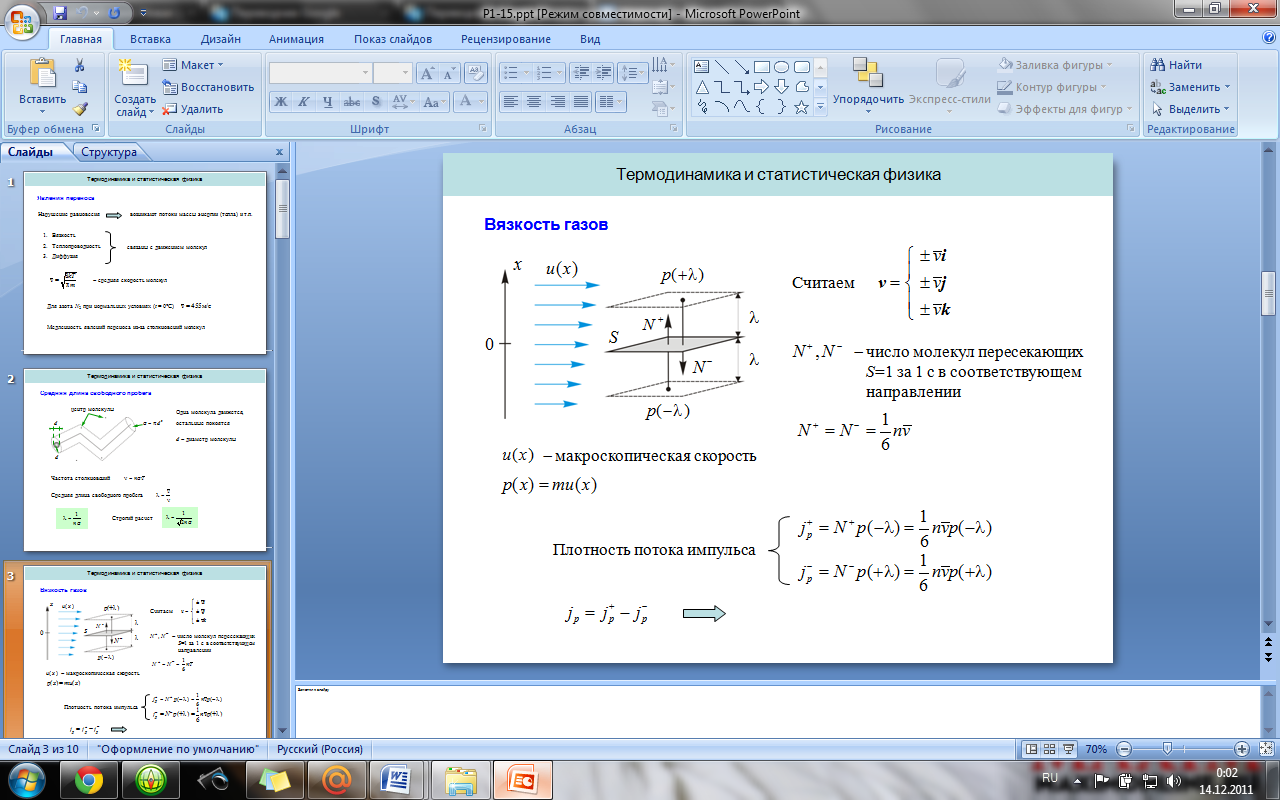
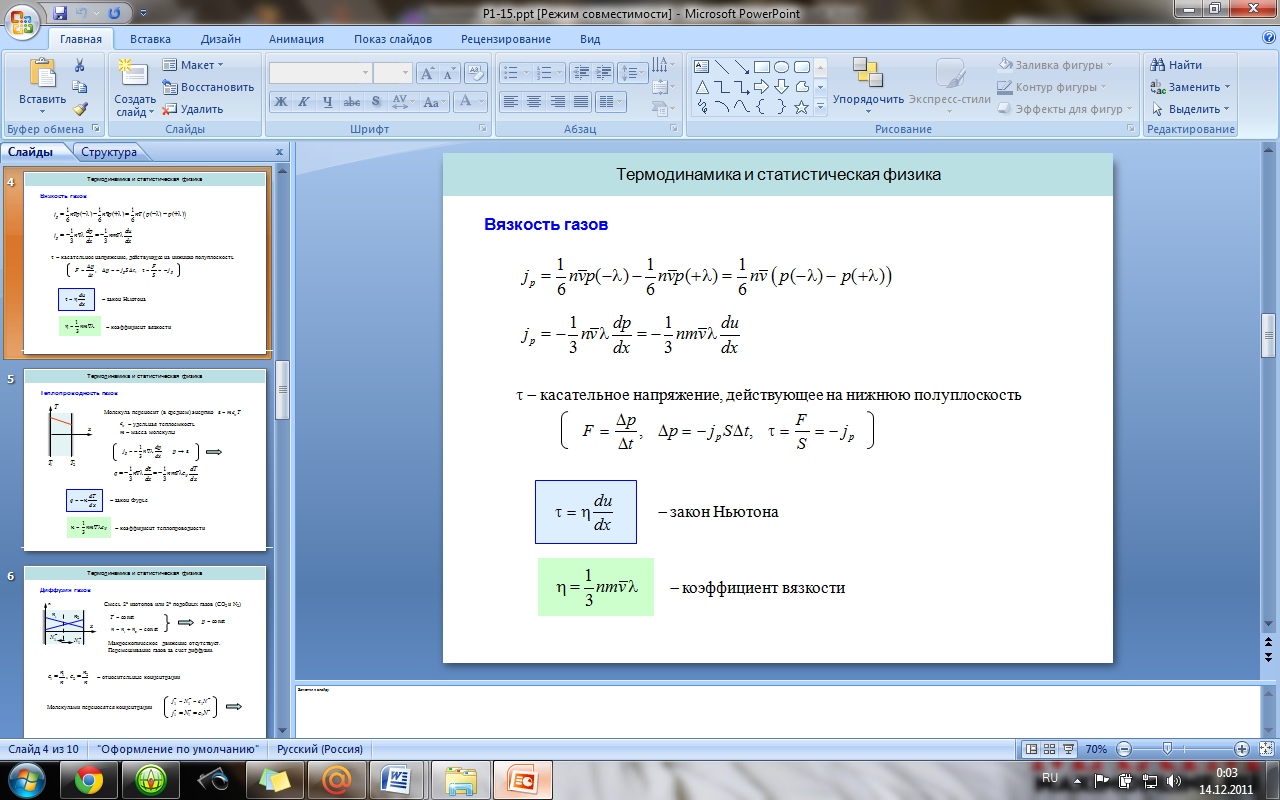
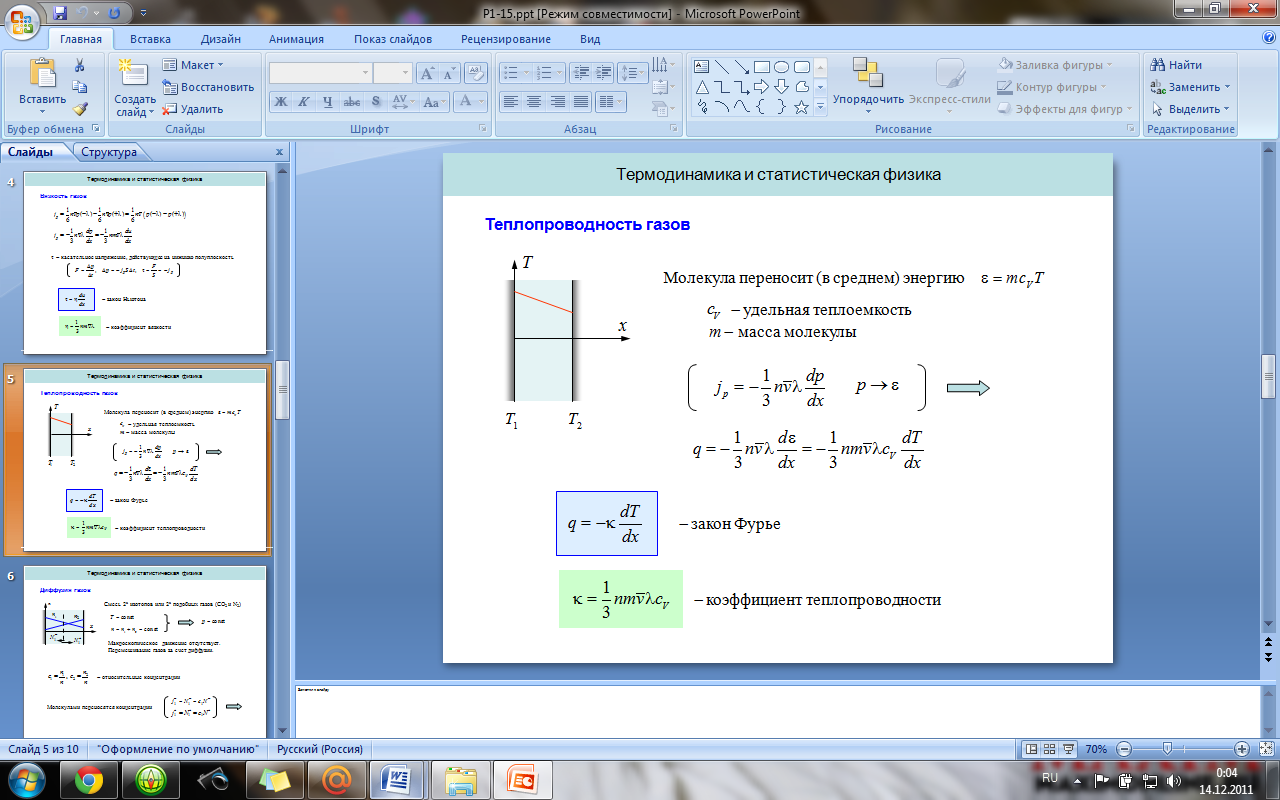
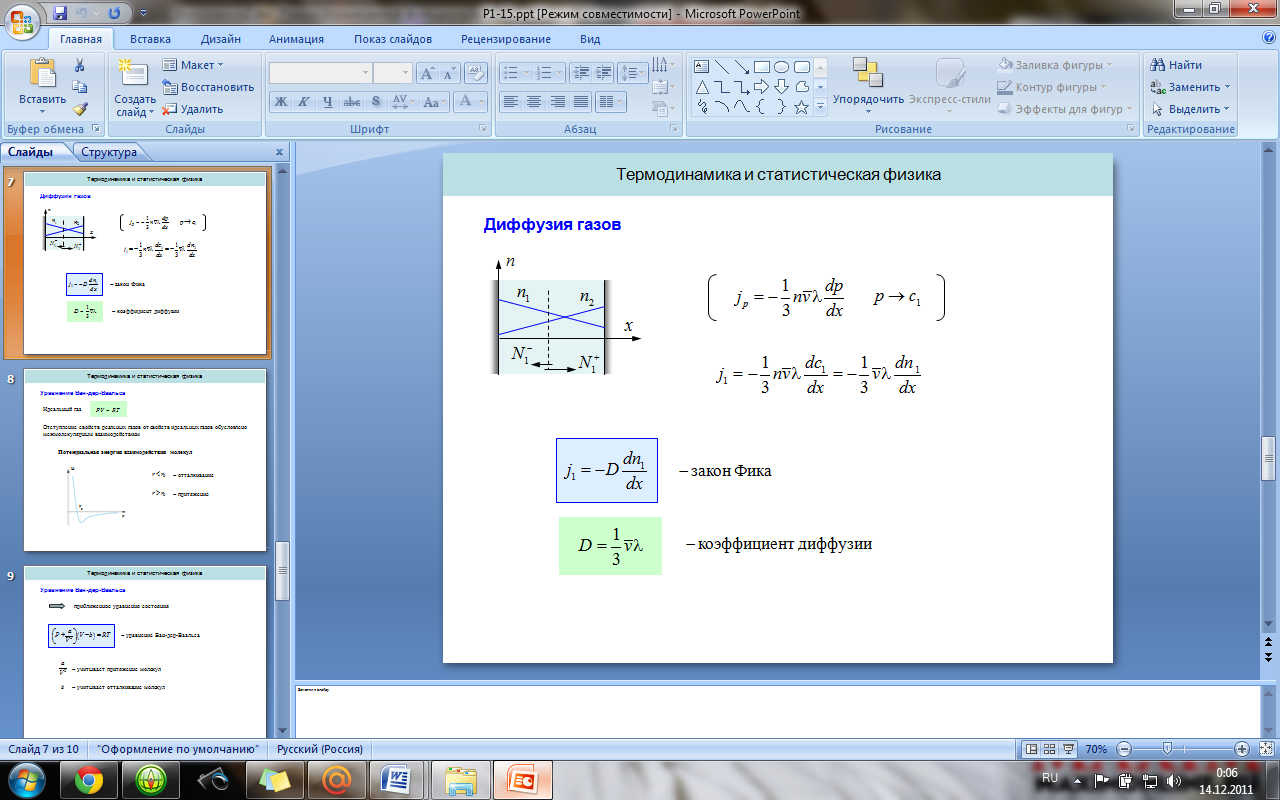
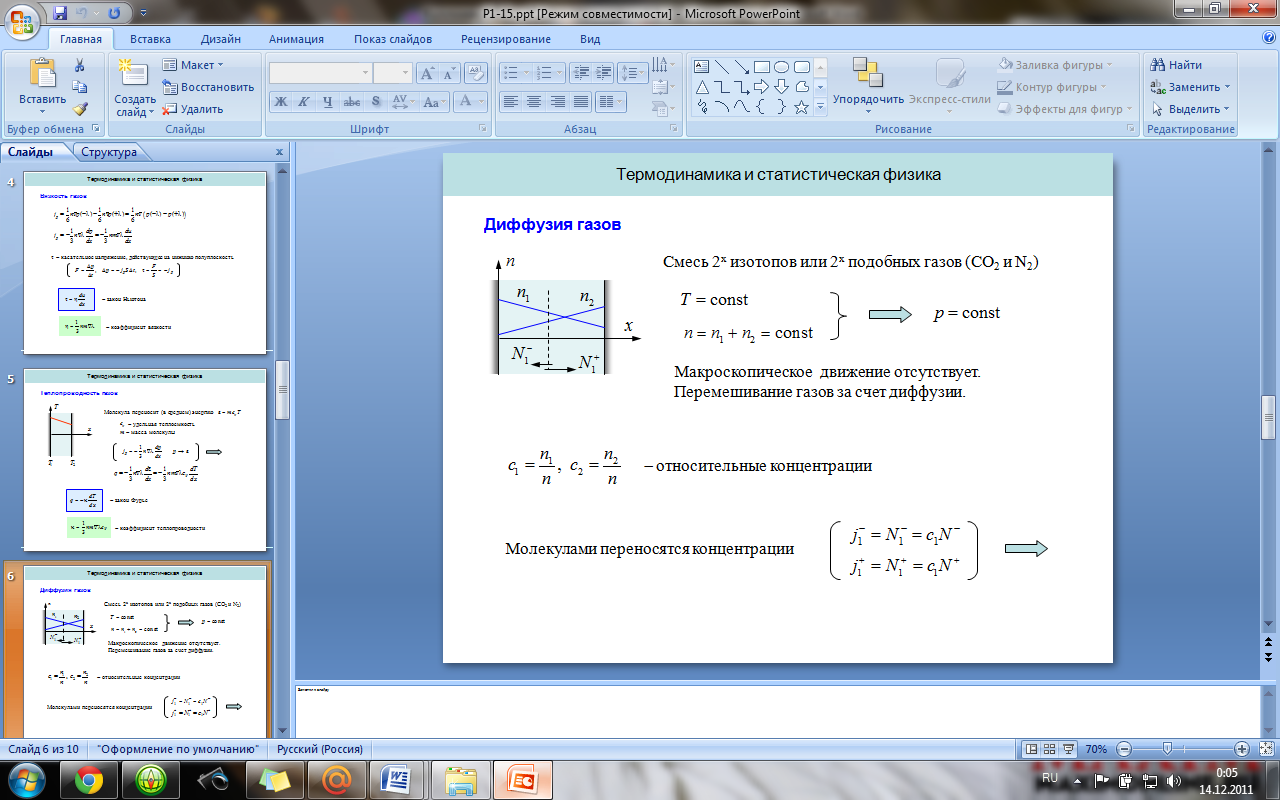
8. Явления переноса. Вязкость, теплопроводность и диффузия газов.

Явление переноса – необратимый процесс, в результате которого происходит пространственный перенос энергии, массы и импульса. Теплопроводность – обусловлена переносом энергии, диффузия – переносом массы. Вязкость – переносом импульса.

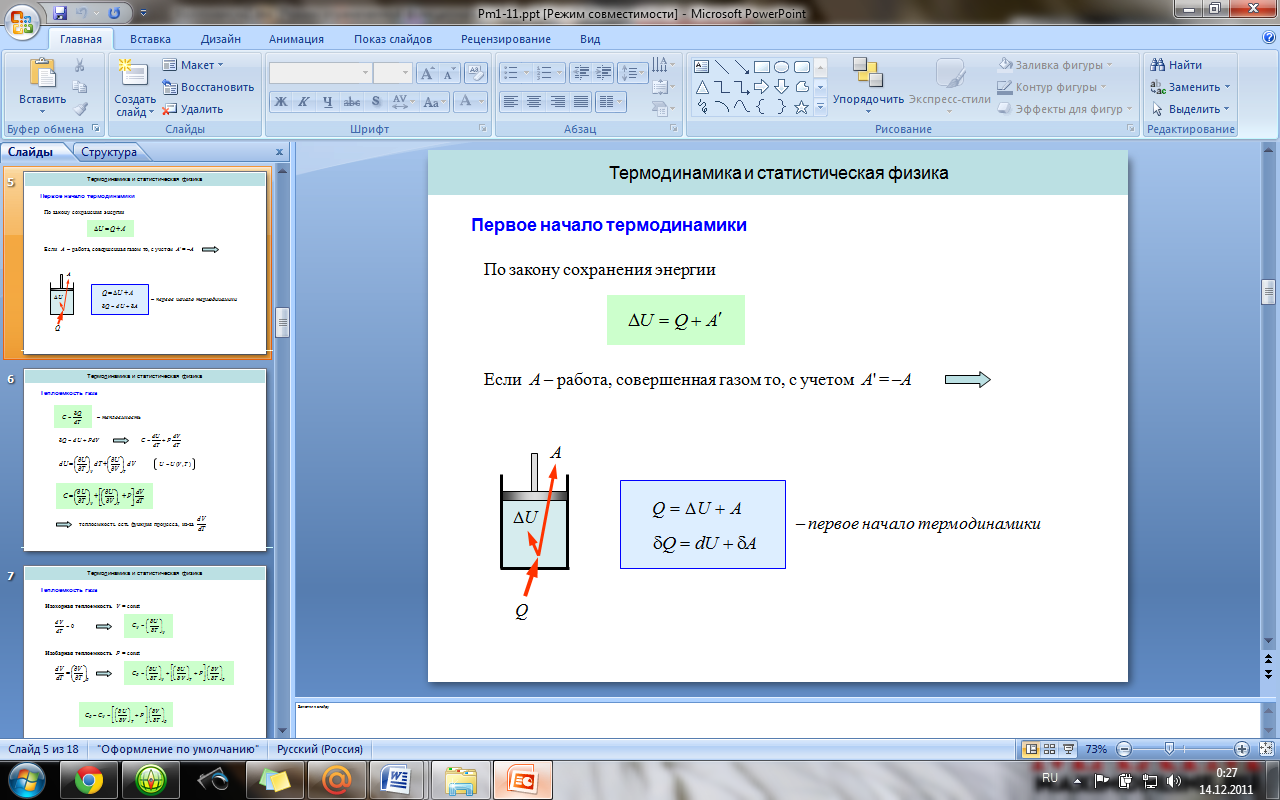
10. Первое начало термодинамики. Применение его для различных процессов.

Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил. Первое начало термодинамики: при изобарном процессе

при изохорном процессе (A = 0)

при изотермическом процессе (ΔU = 0)

Здесь  — масса газа,  — молярная масса газа,  — молярная теплоёмкость при постоянном объёме,  — давление, объём и температура газа соответственно, причём последнее равенство верно только для идеального газа.

12. Изопроцессы, изопроцессы идеального газа.

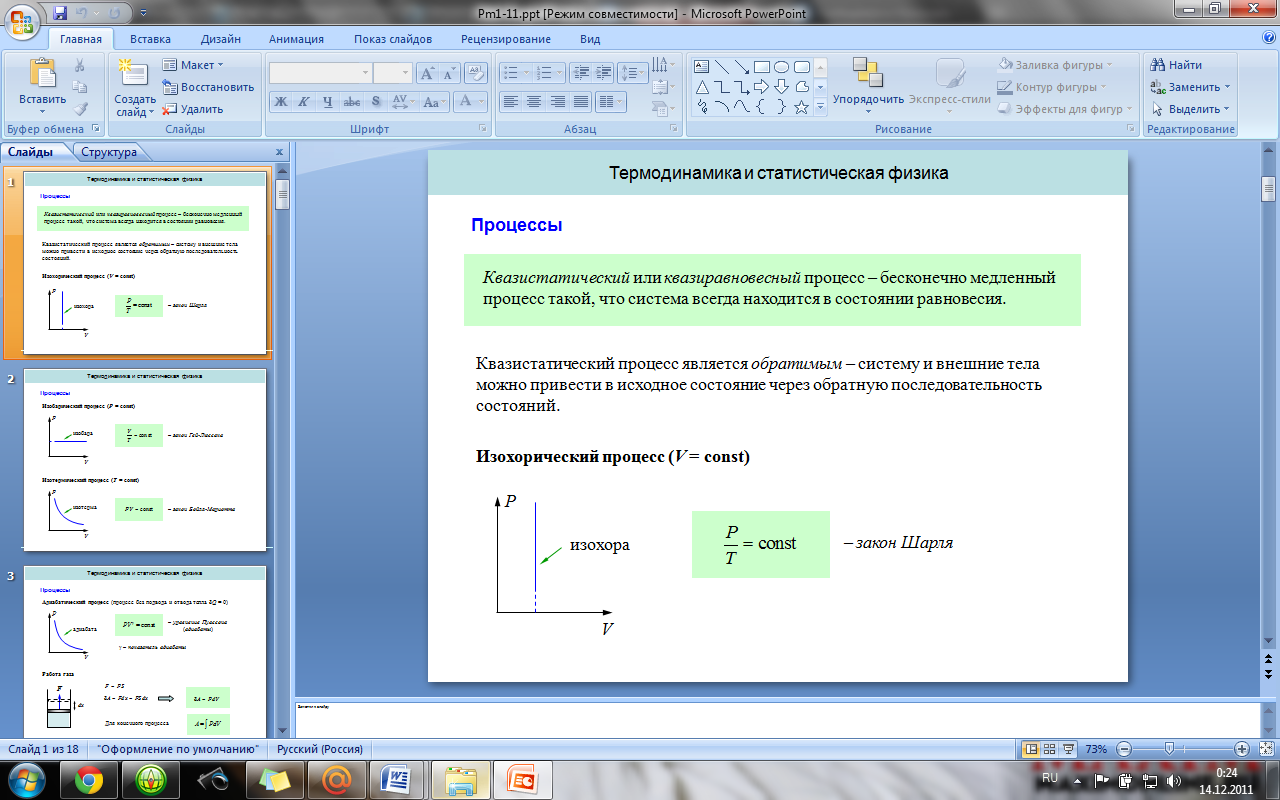
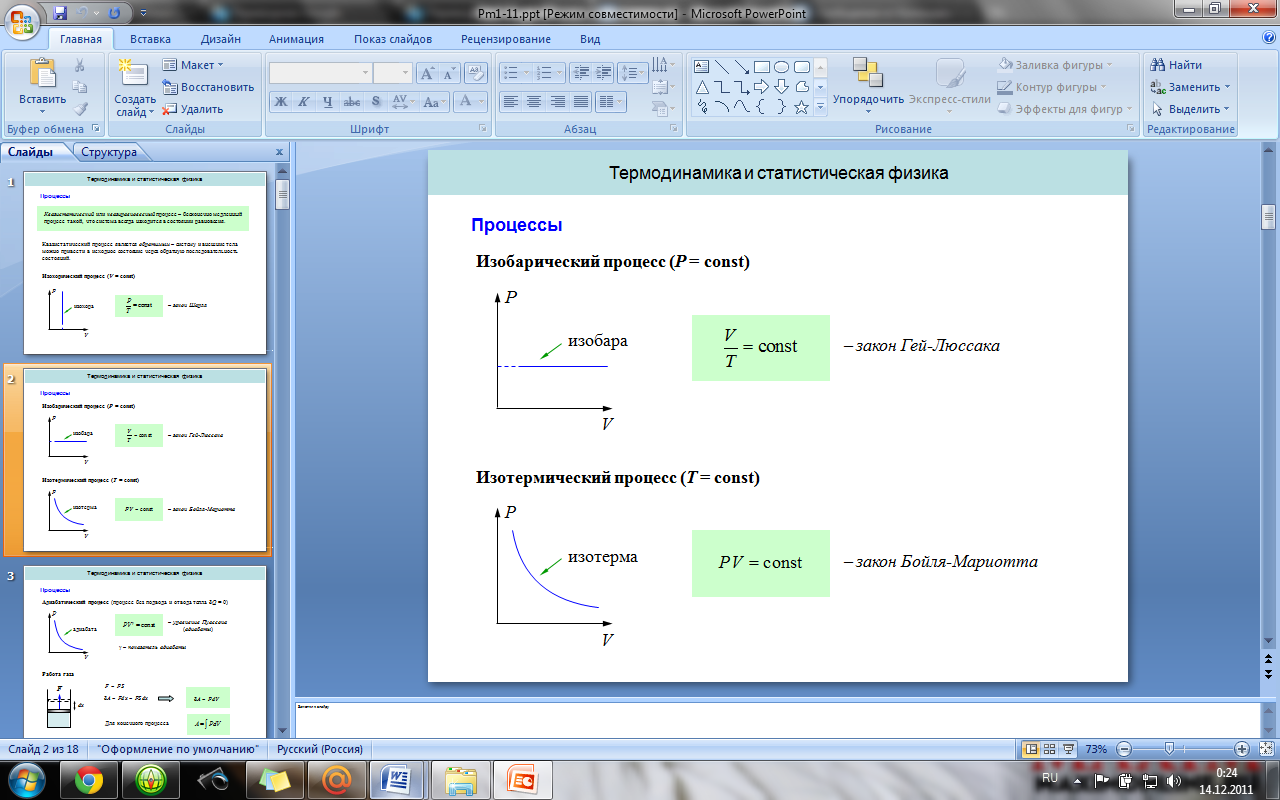
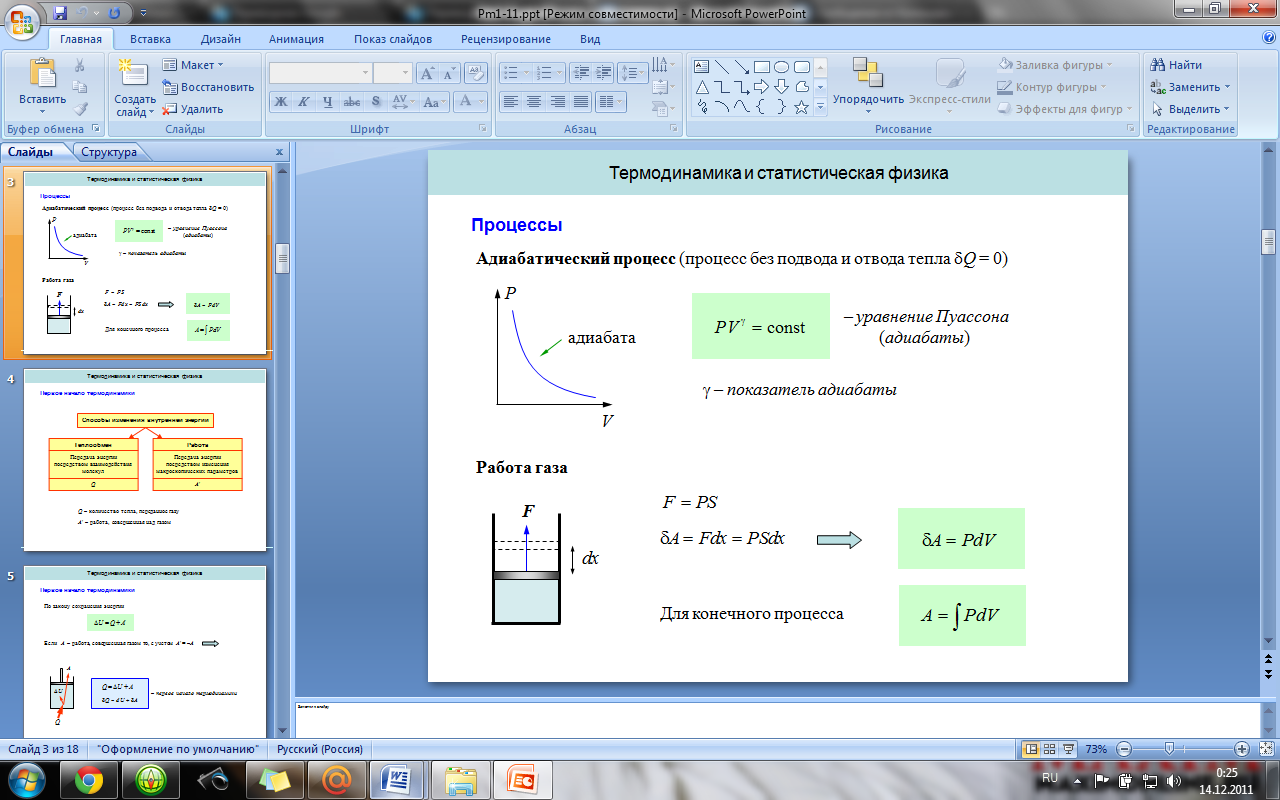
Изопроцессы — термодинамические процессы, во время которых количество вещества и ещё одна из физических величин — параметров состояния: давление, объём или температура — остаются неизменными.

14. Круговые процессы. Тепловой двигатель. Цикл Карно и теорема Карно.

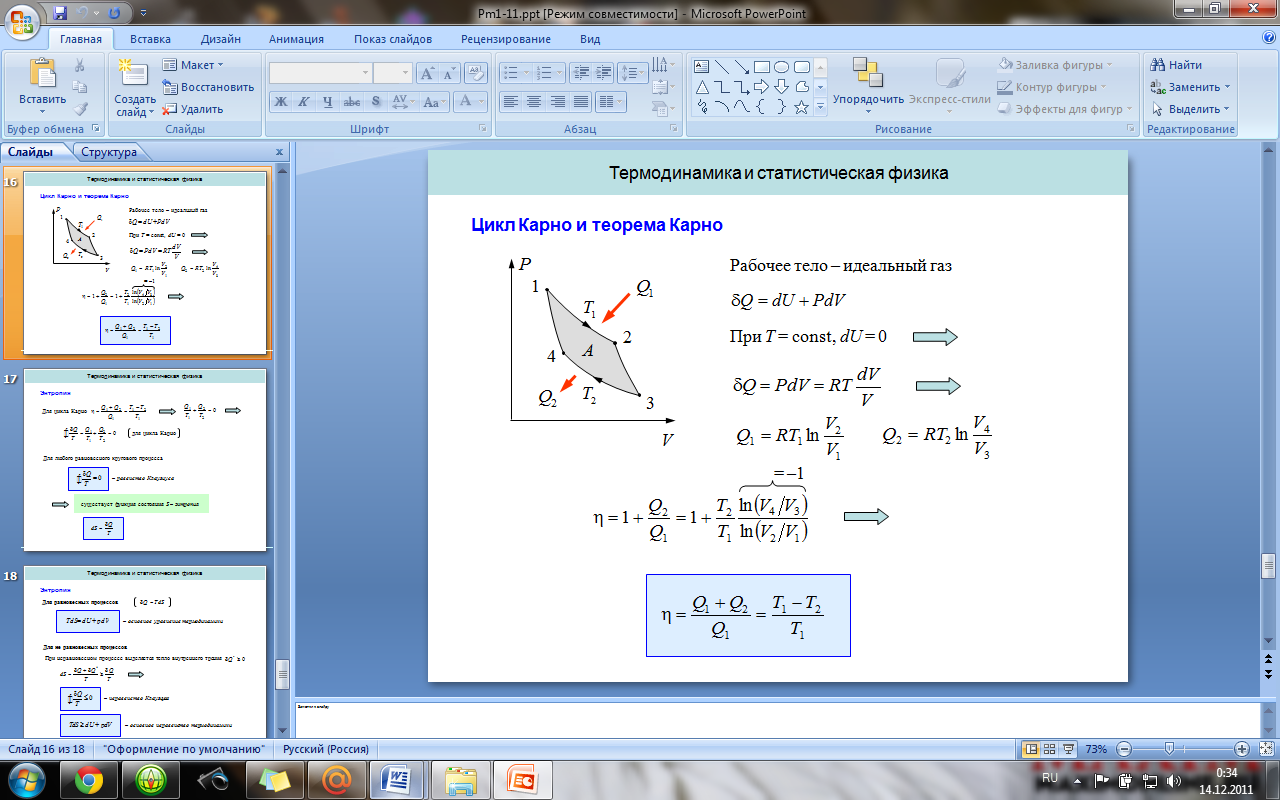
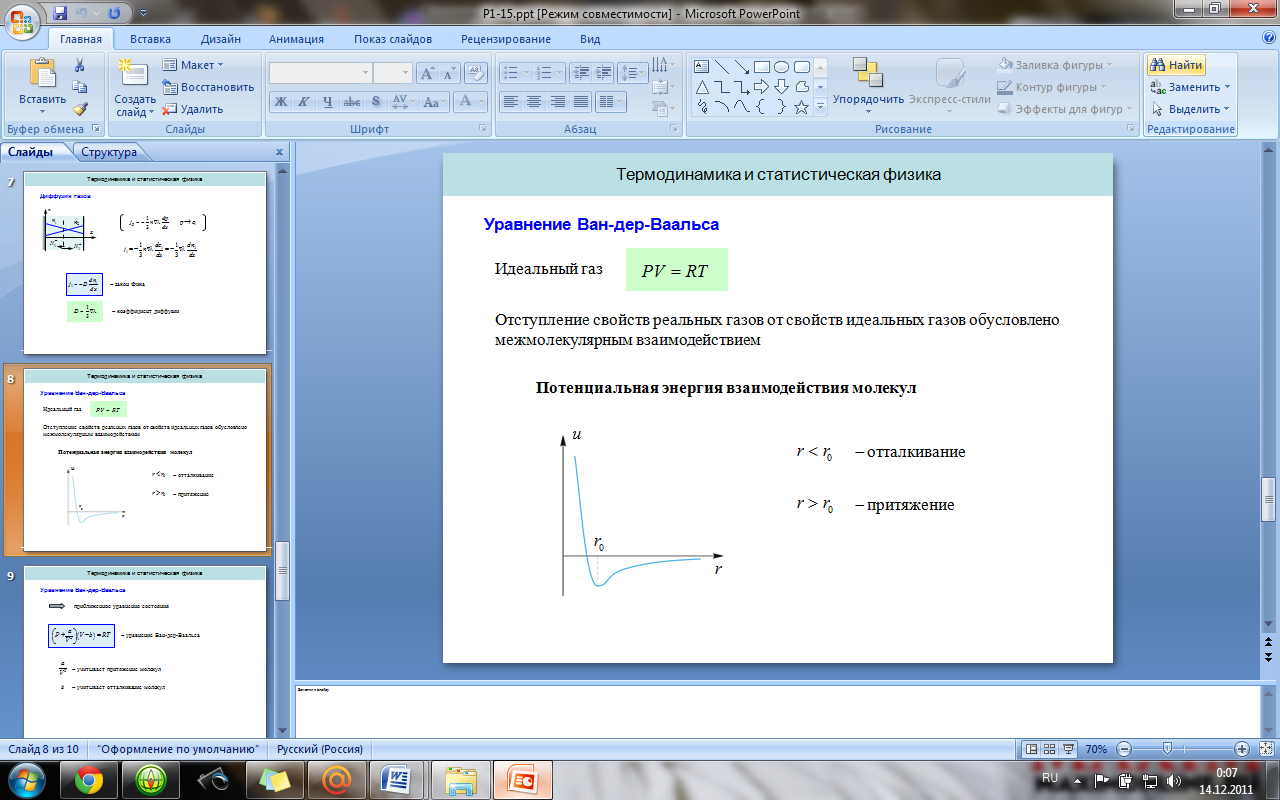
16. Реальные газы. Уравнение Ван-дер-Ваальса.

Р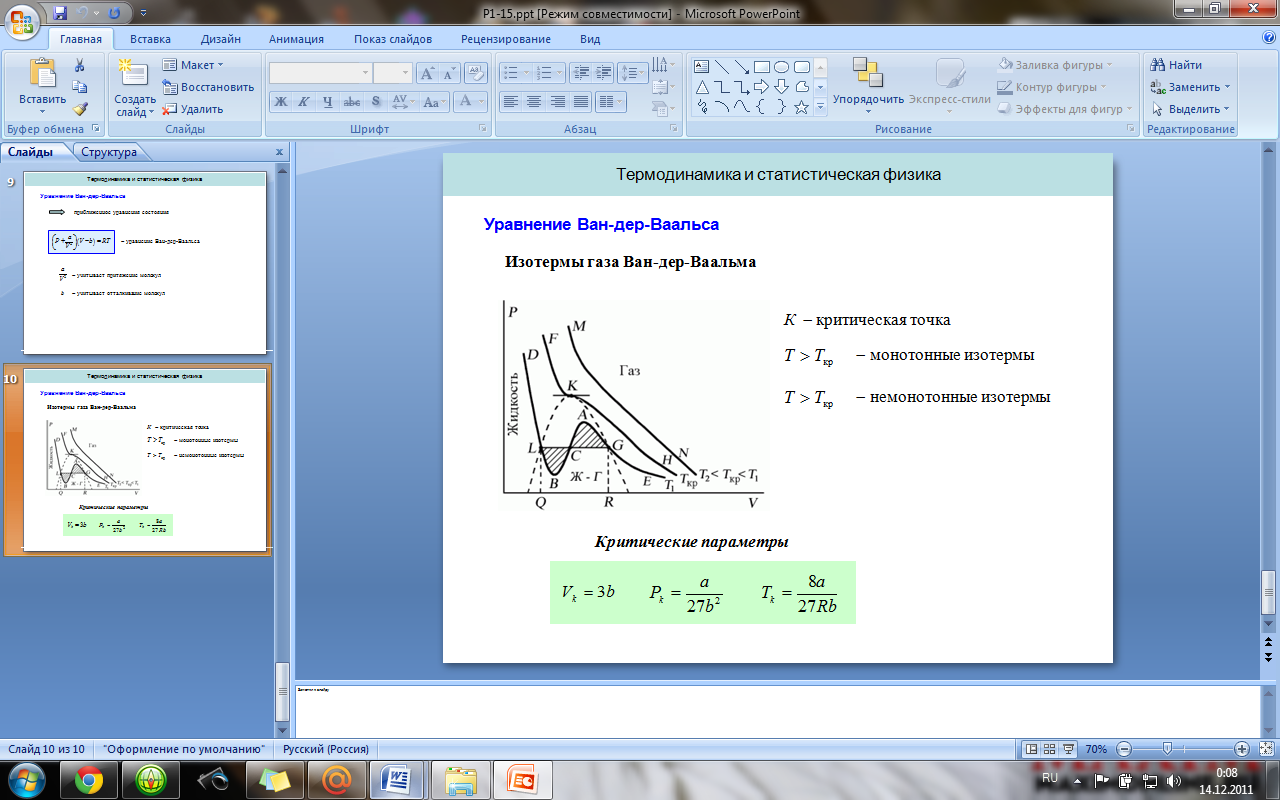еальный газ — газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева. Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объём.

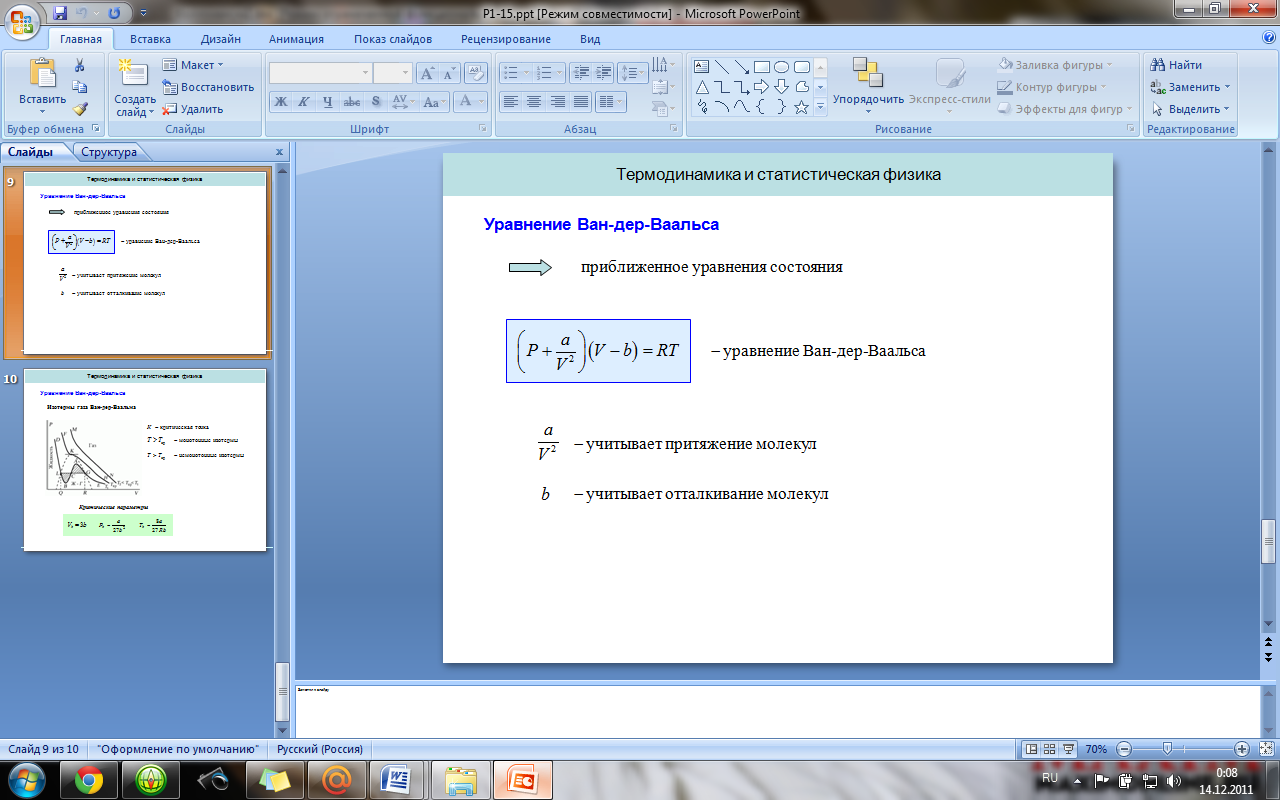
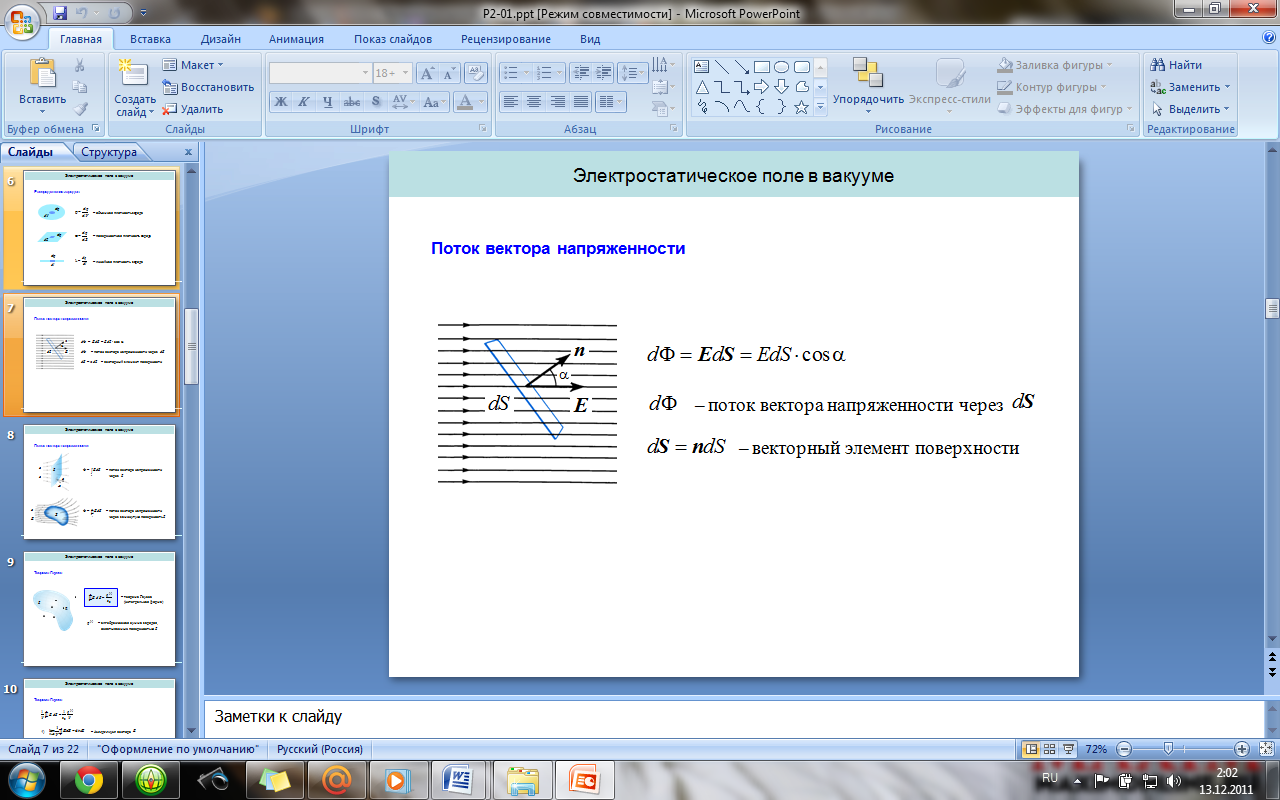
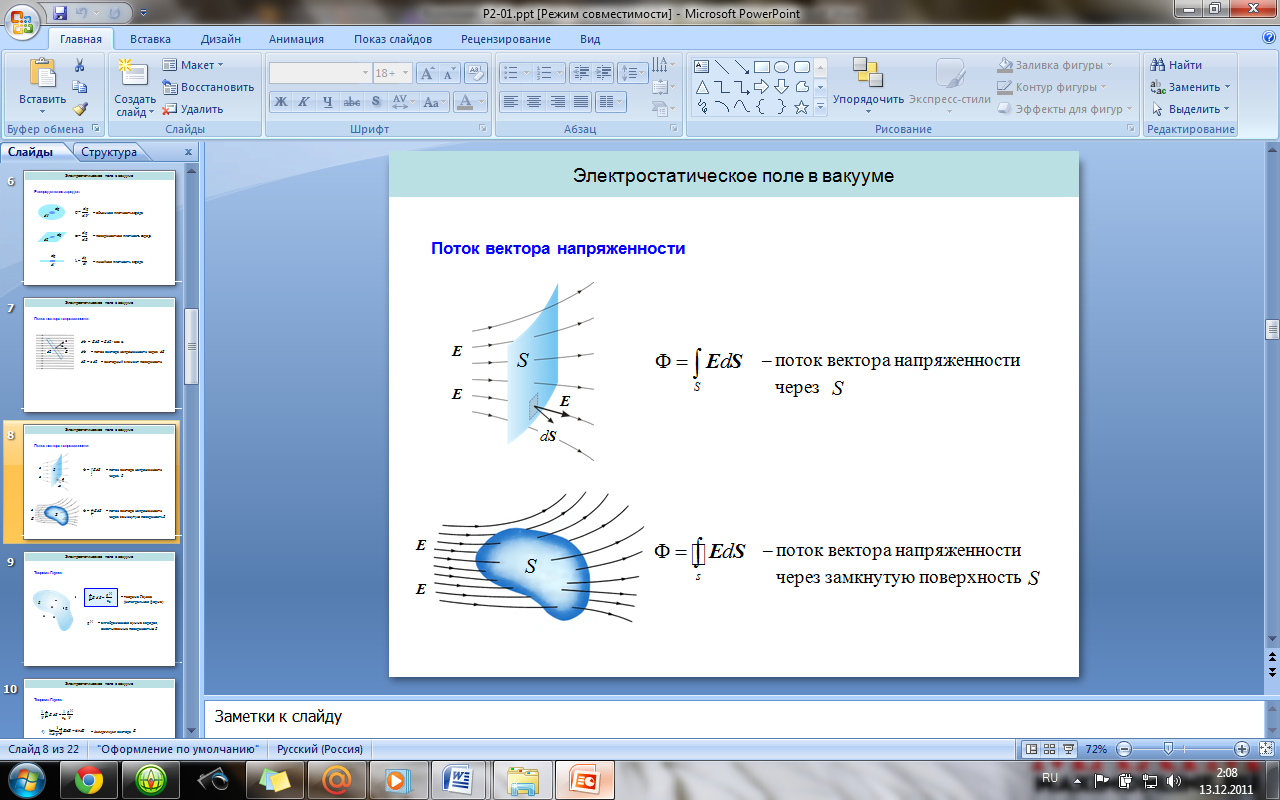
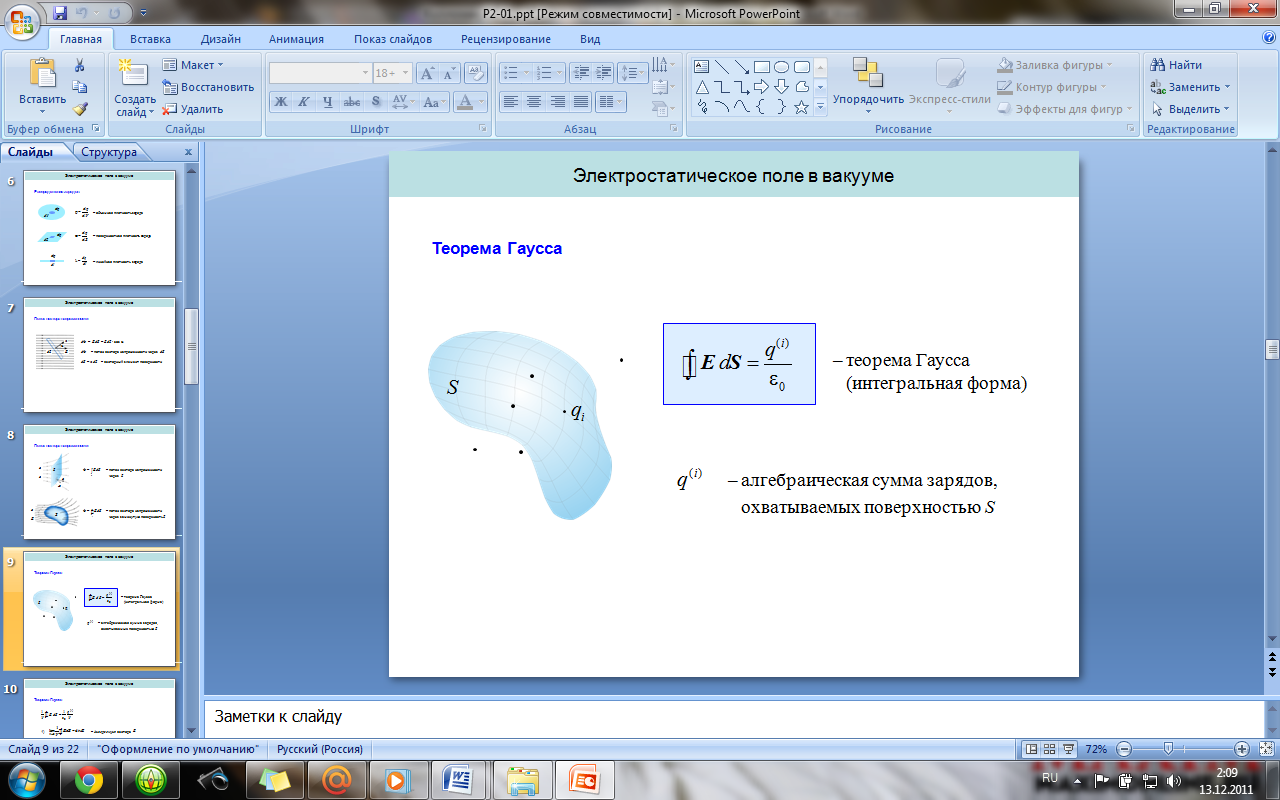
18. Поток вектора E. Теорема Гаусса для вектора E (в интегральной и дифференциальной формах).

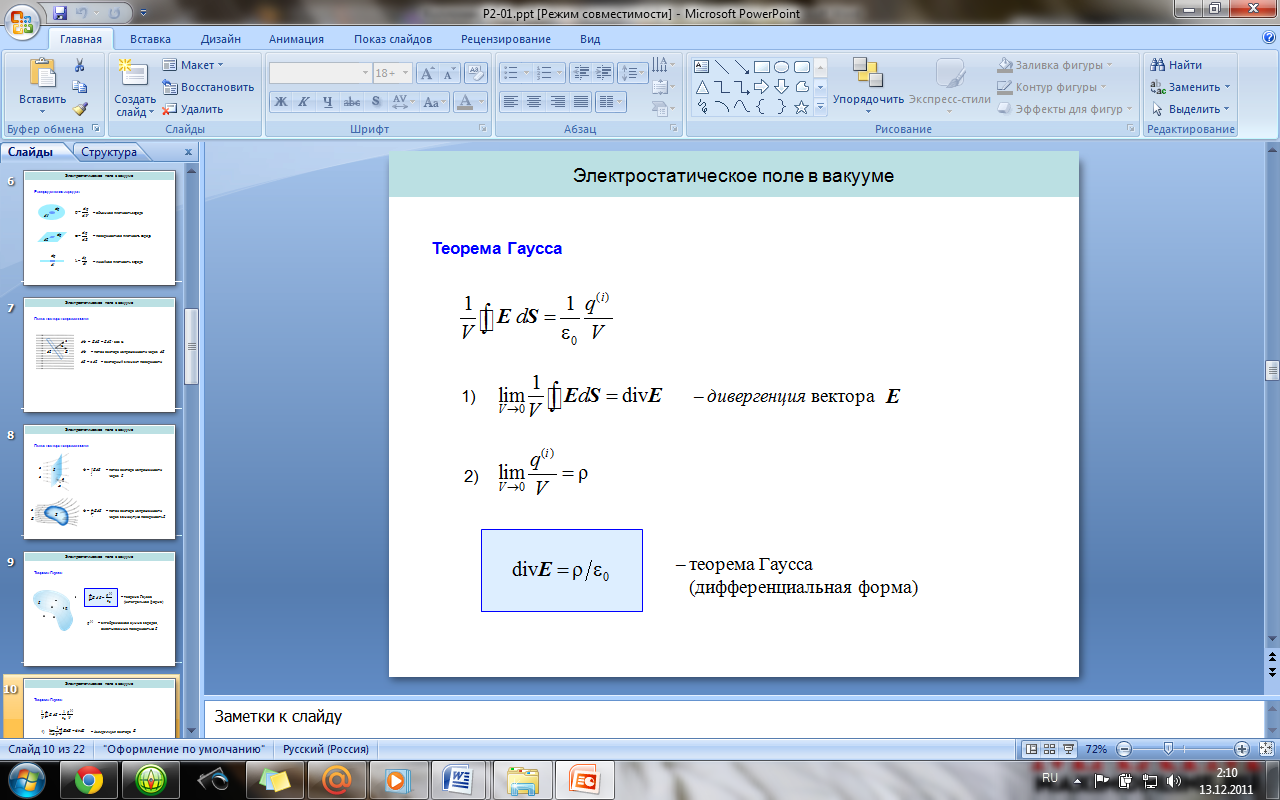
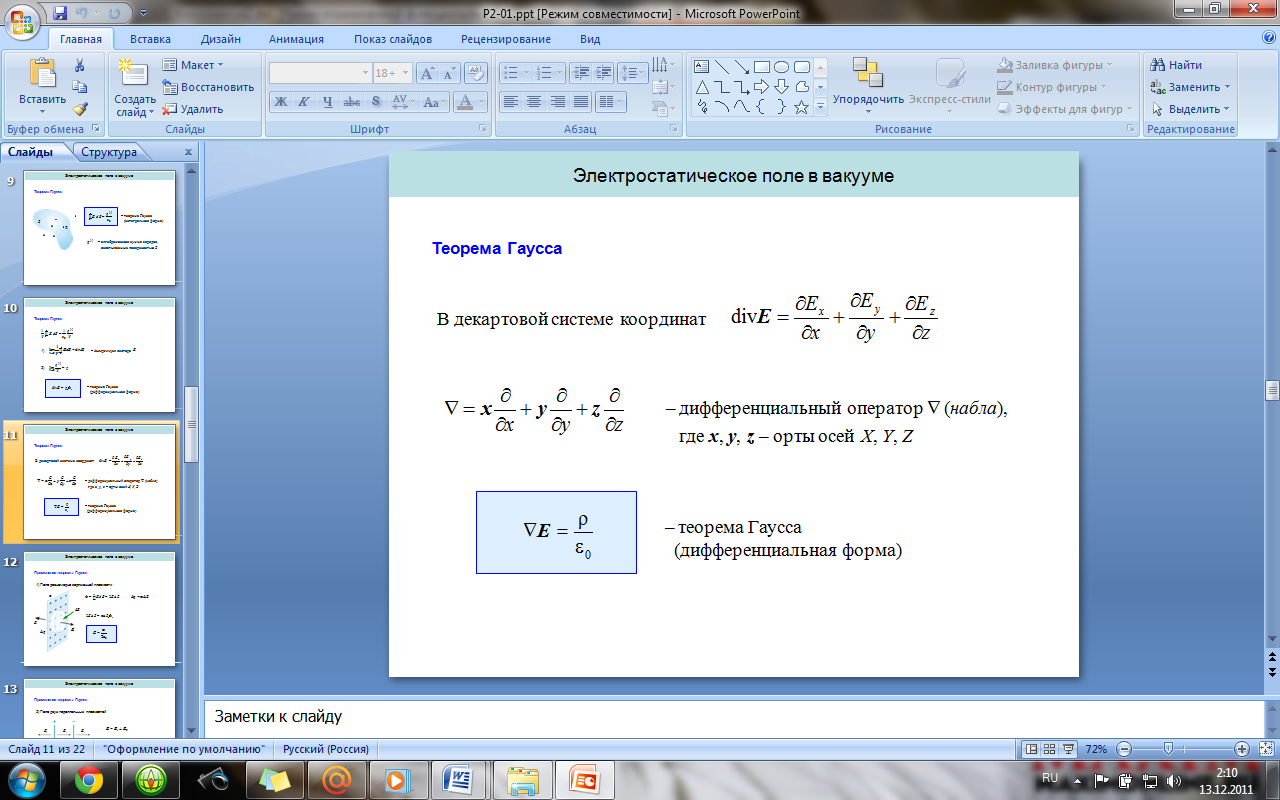
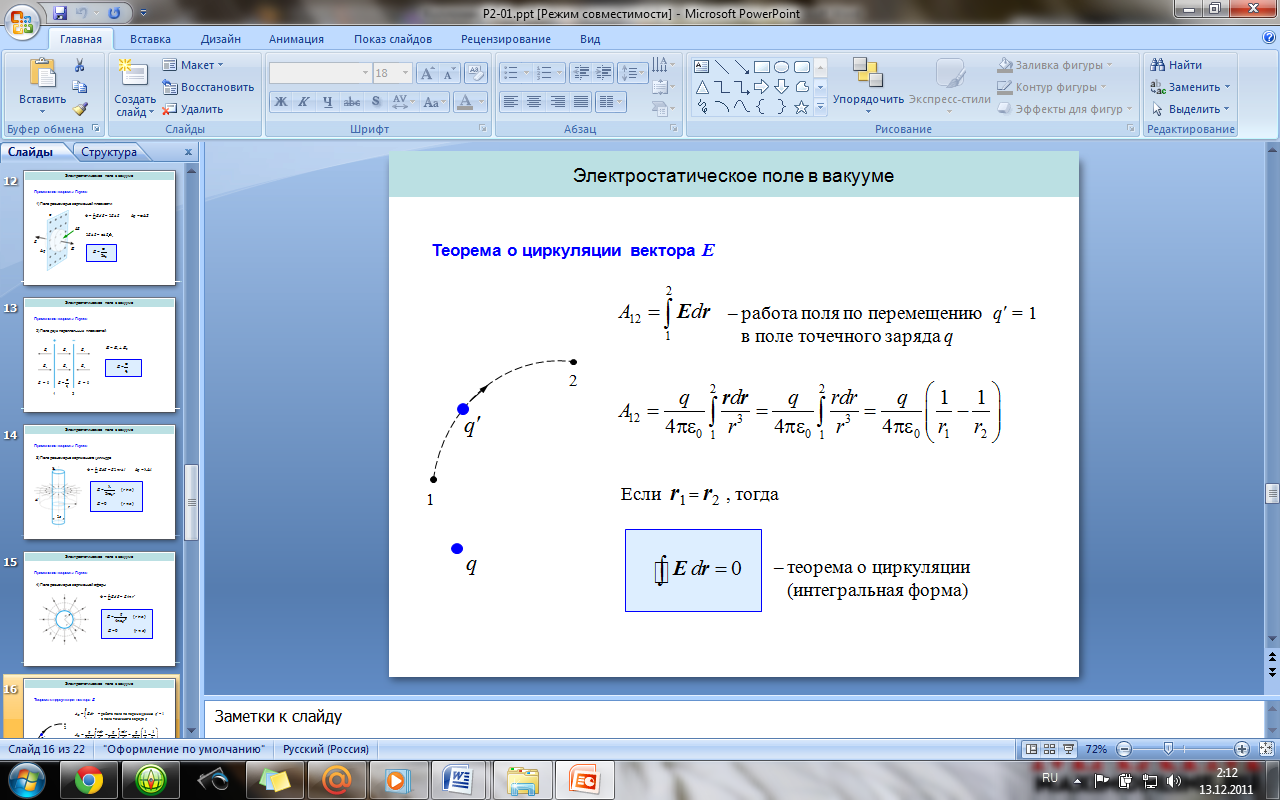
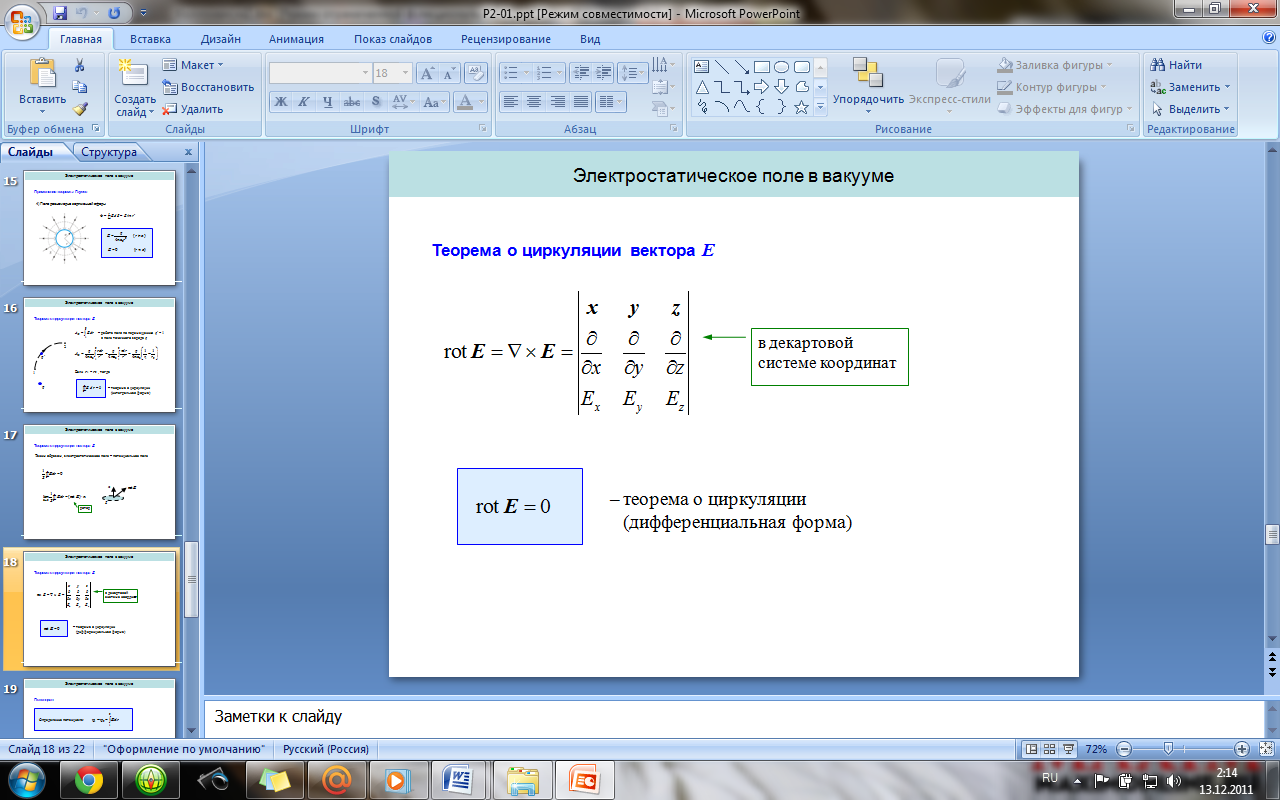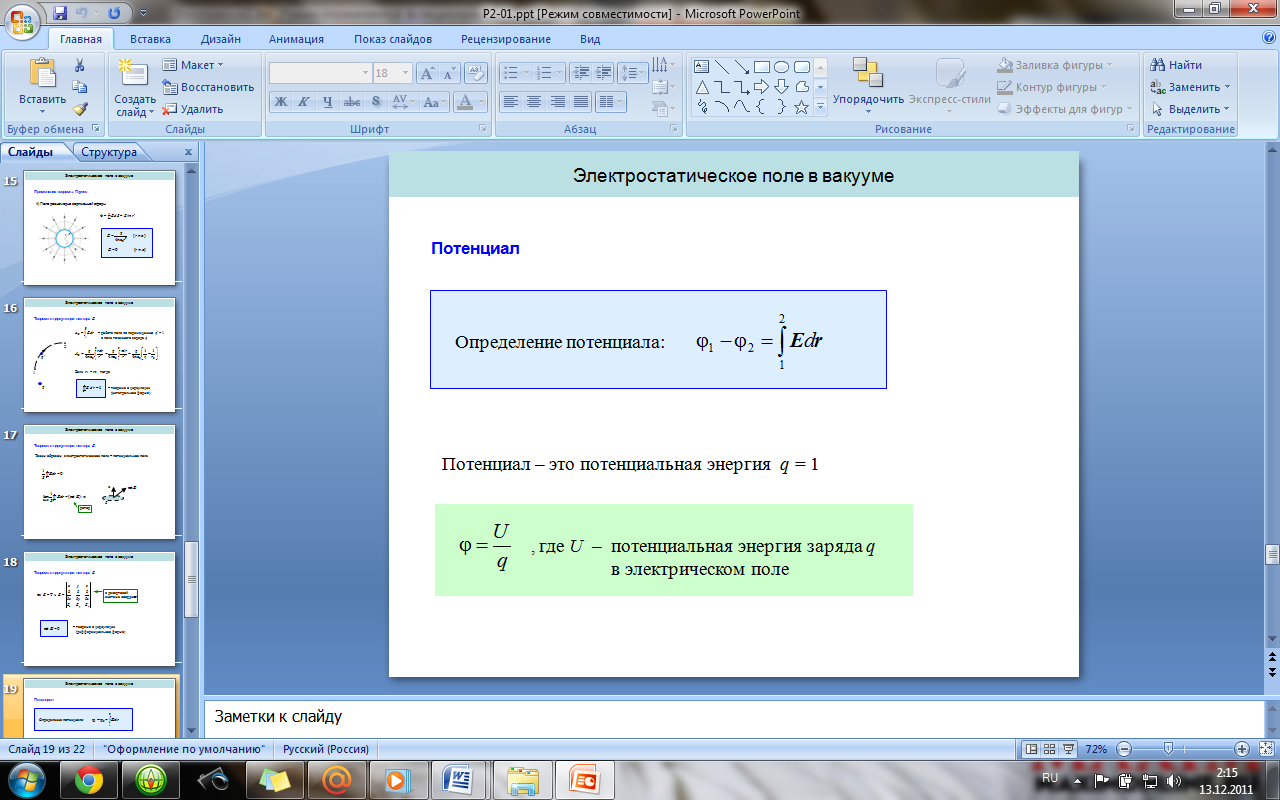
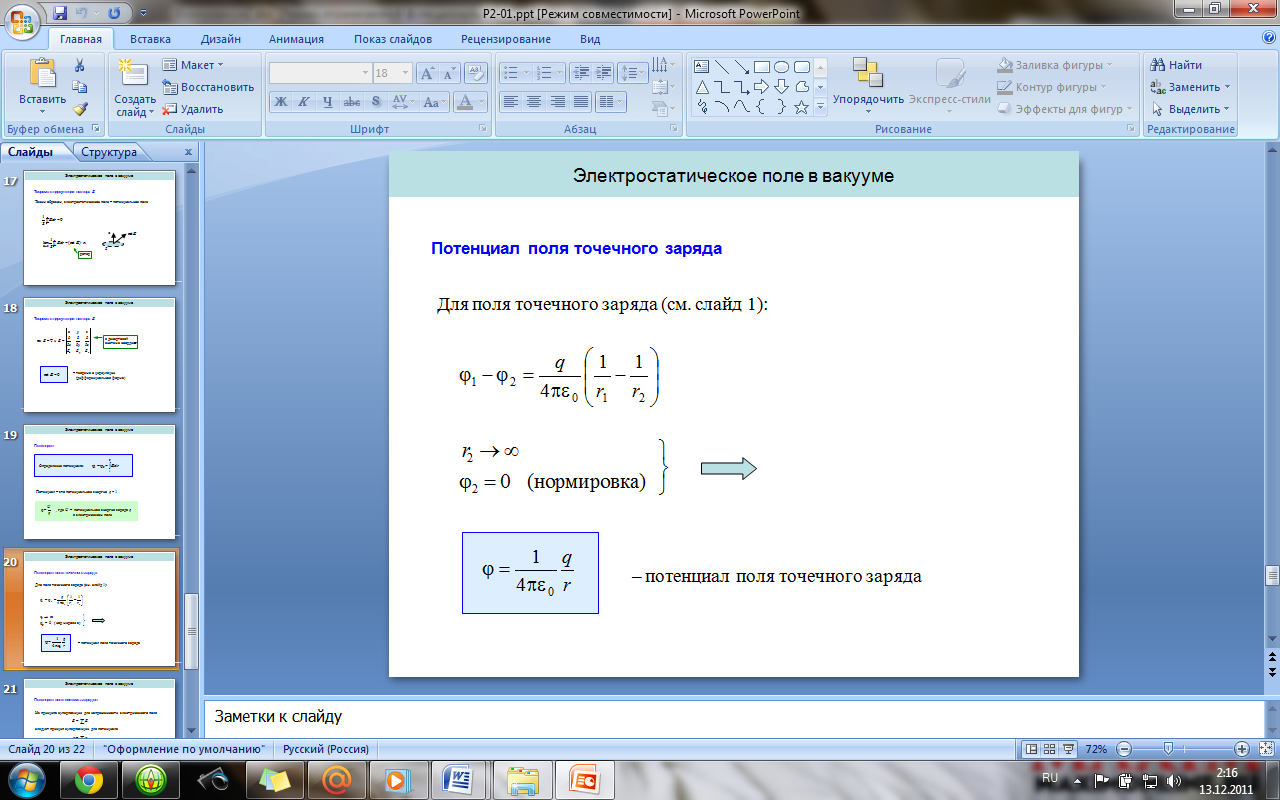
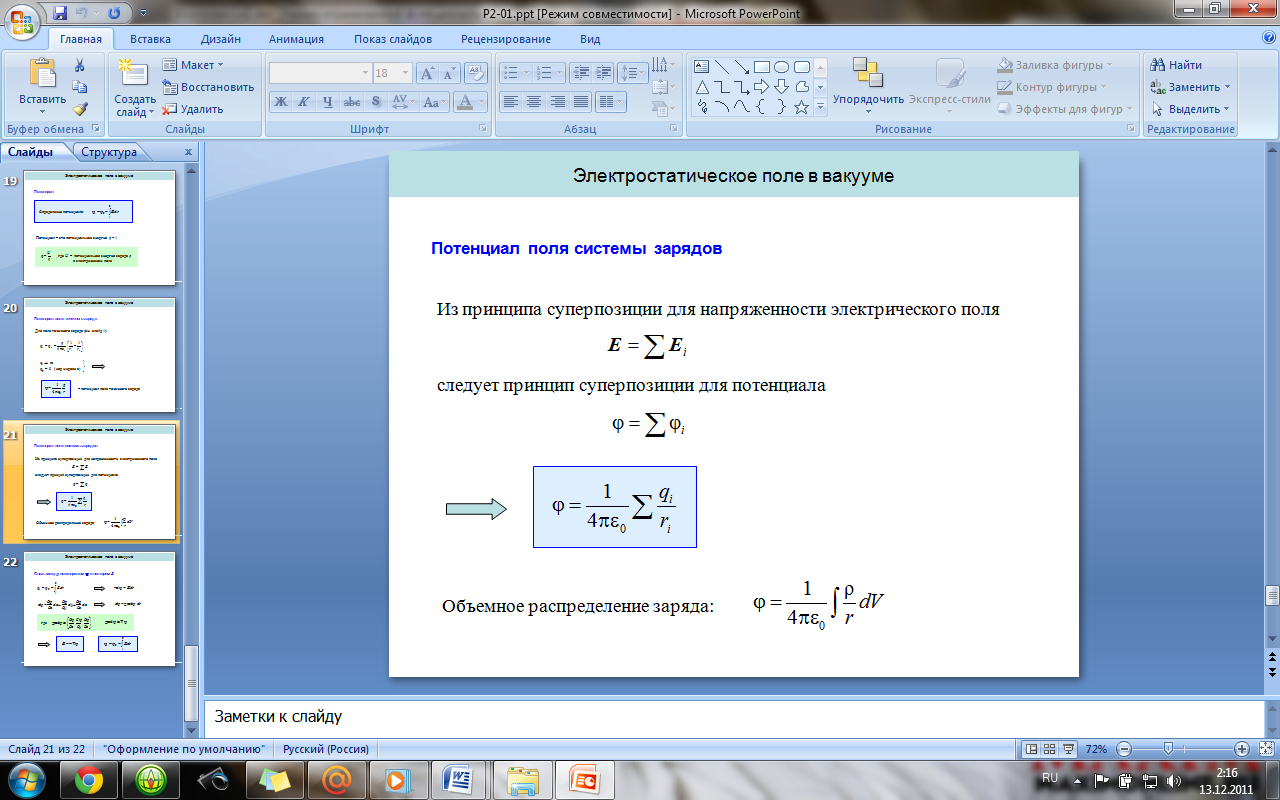
20. Циркуляция вектора E. Теорема о циркуляции вектора E (в дифференциальной и интегральной формах). Потенциал. Потенциал точечного заряда и системы зарядов.

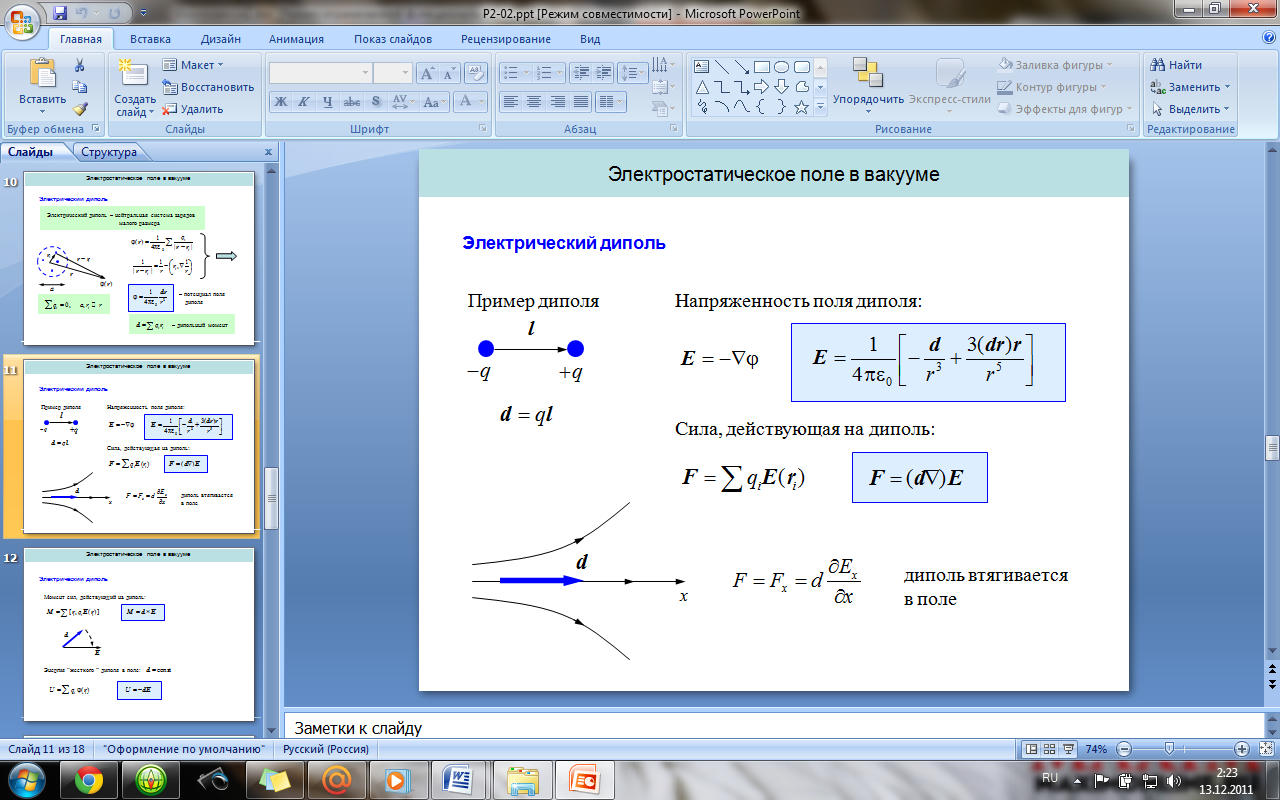
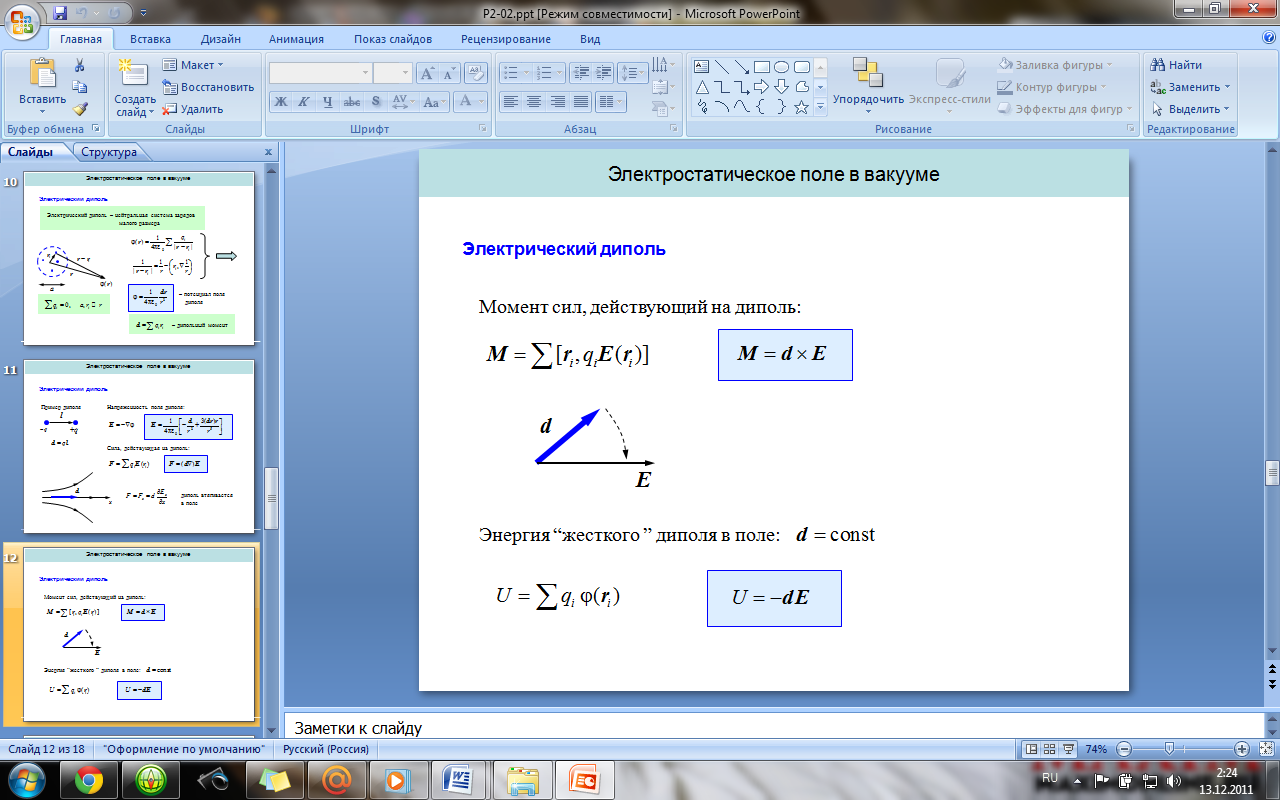
2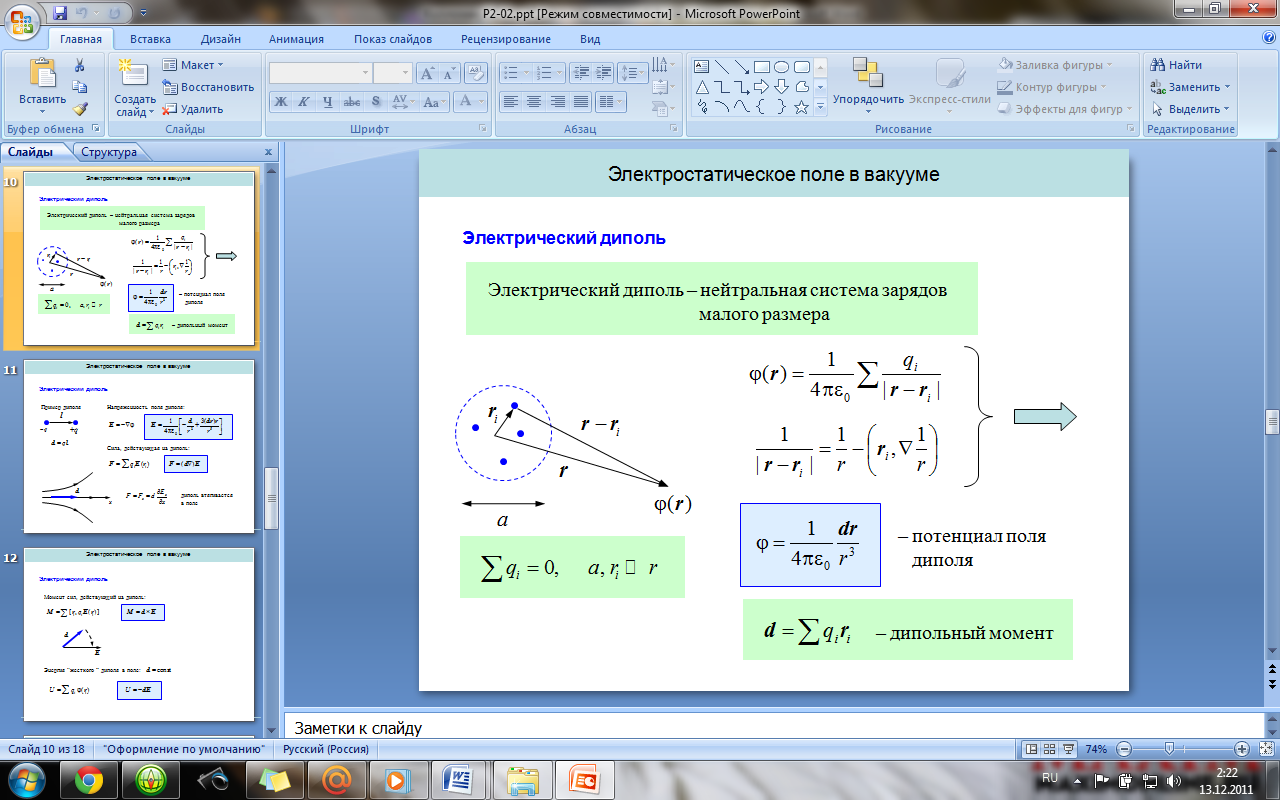2. Электрический диполь. Электрический момент диполя. Поле диполя. Сила и момент сил, действующие на диполь в электрическом поле.

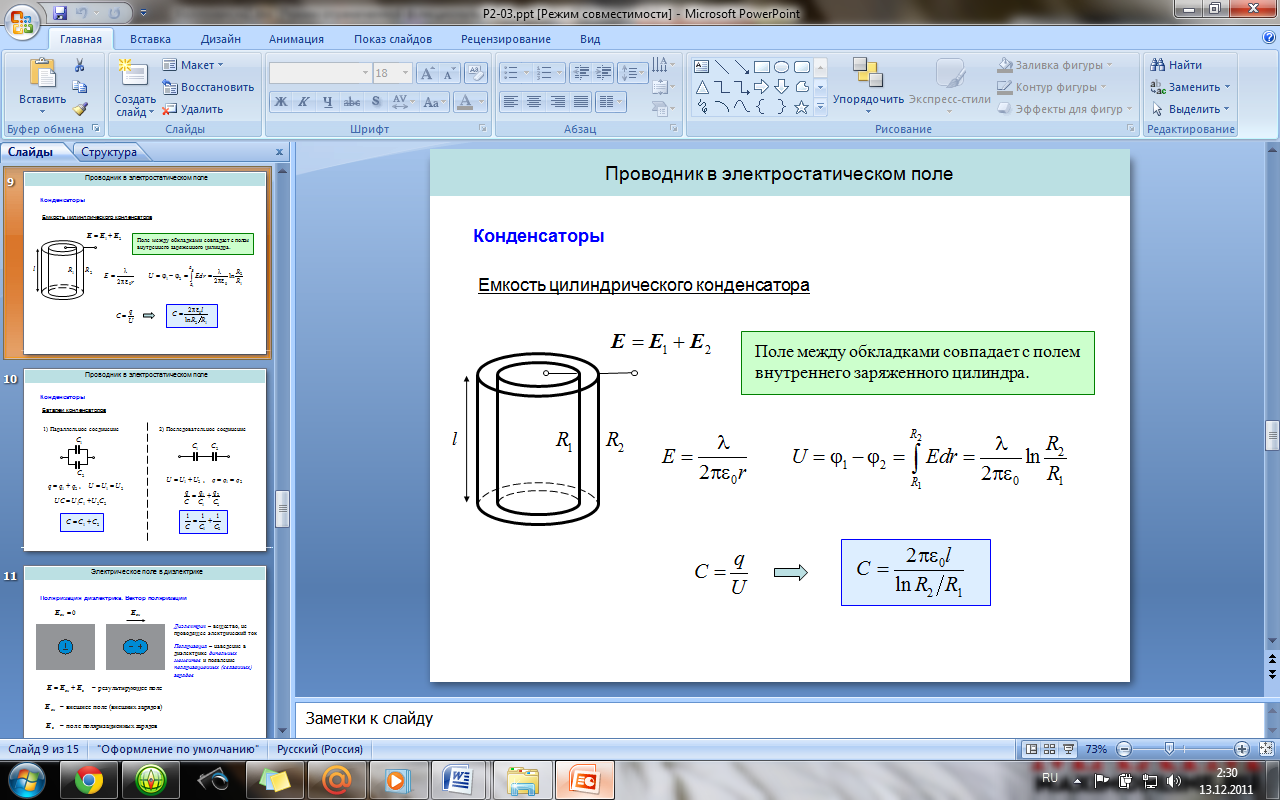
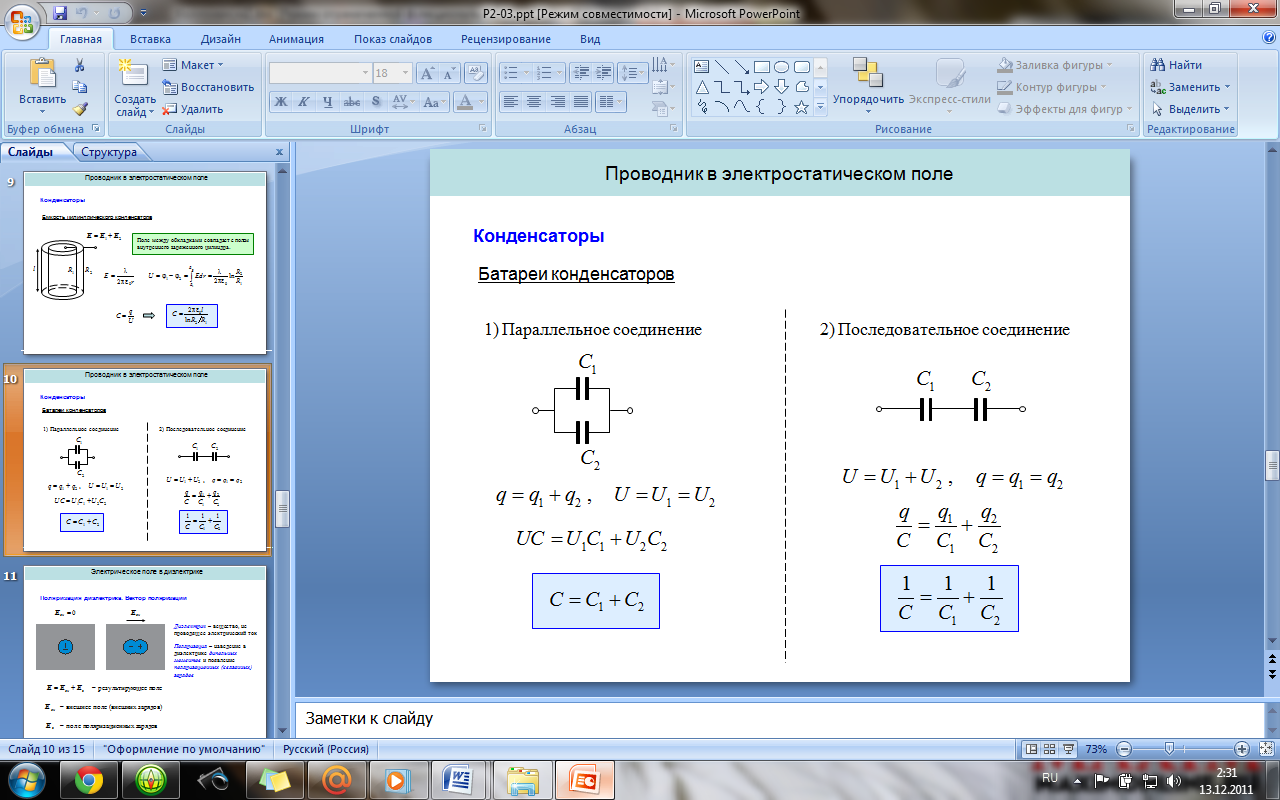
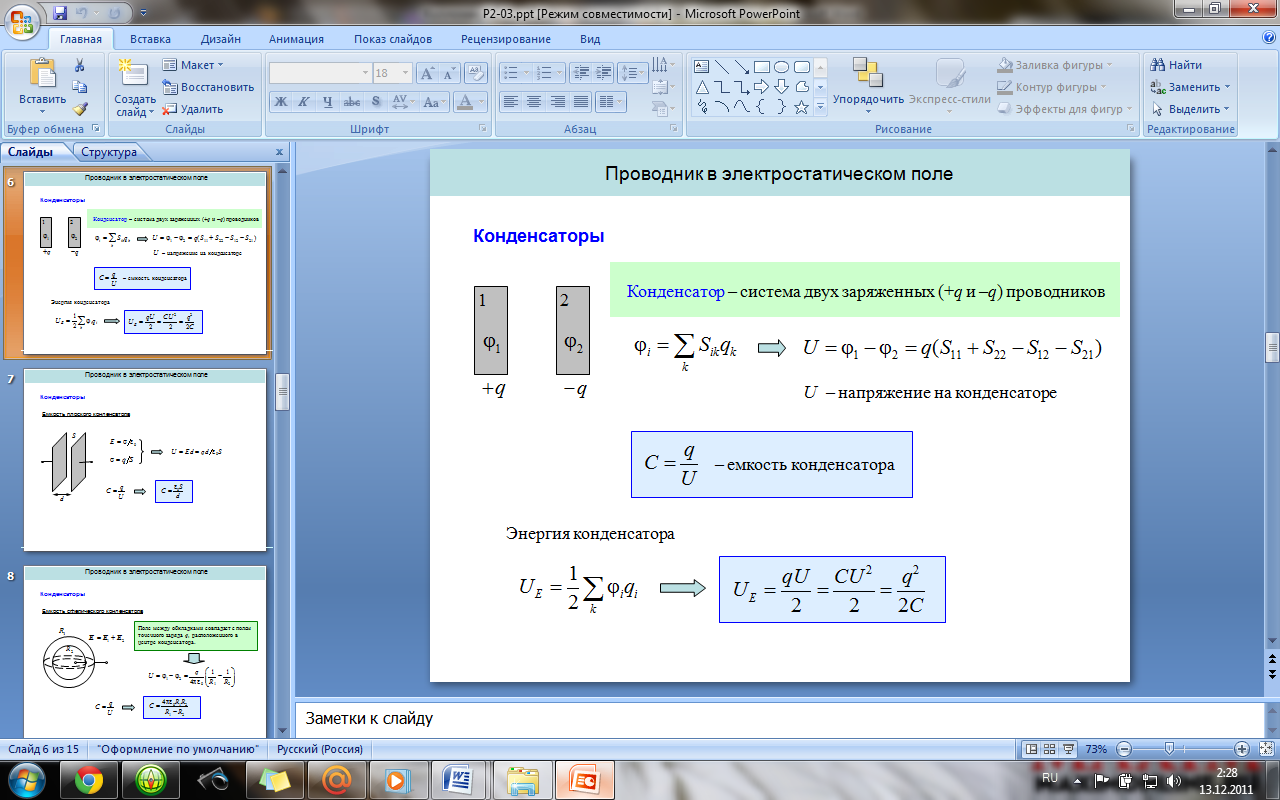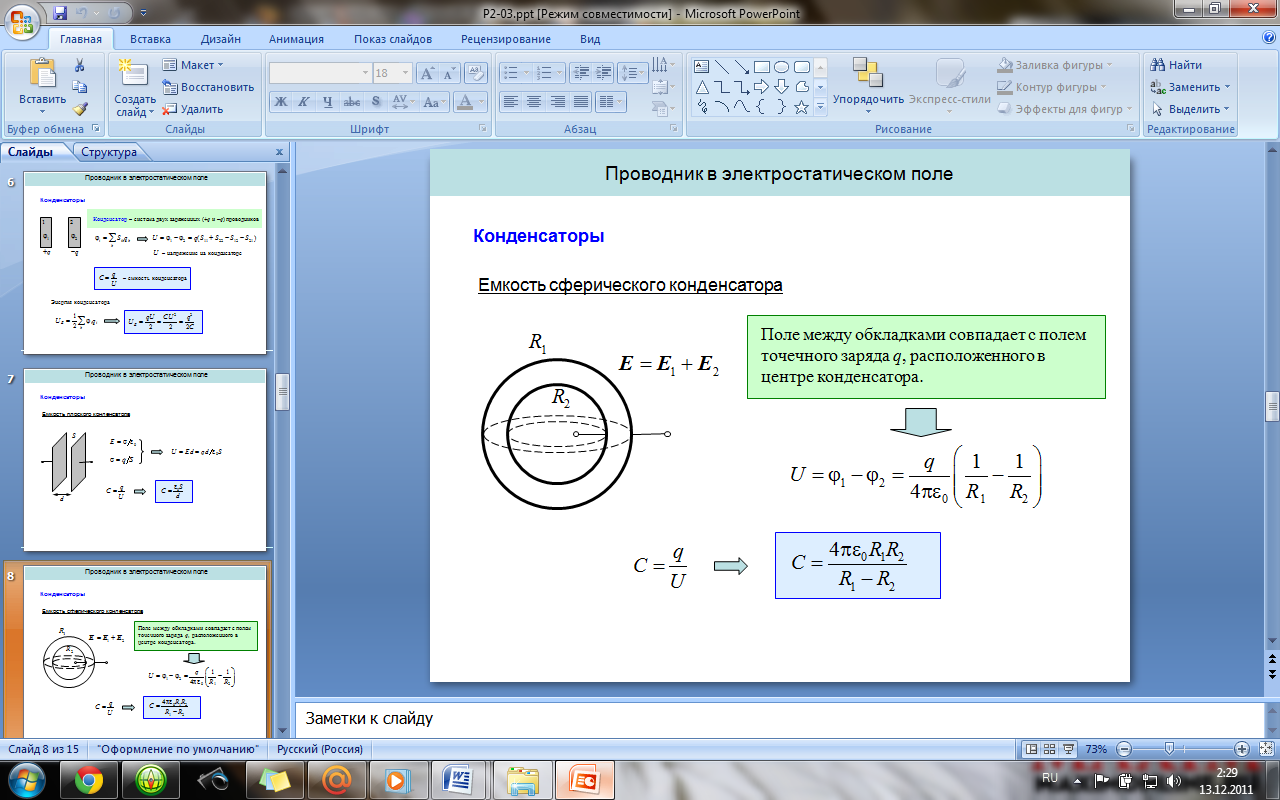
24. Конденсаторы. Емкость и энергия конденсатора. Емкость плоского, цилиндрического и сферического конденсаторов. Последовательное и параллельное соединение конденсаторов.

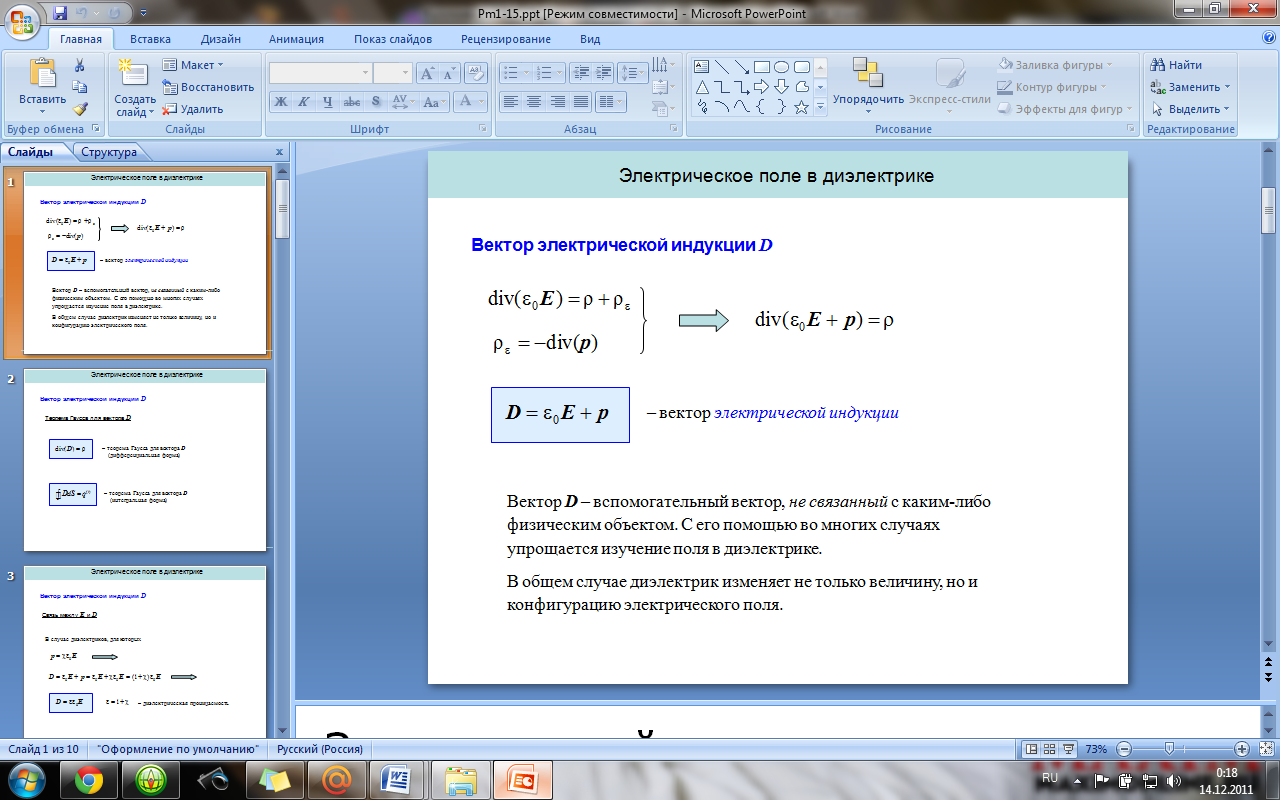
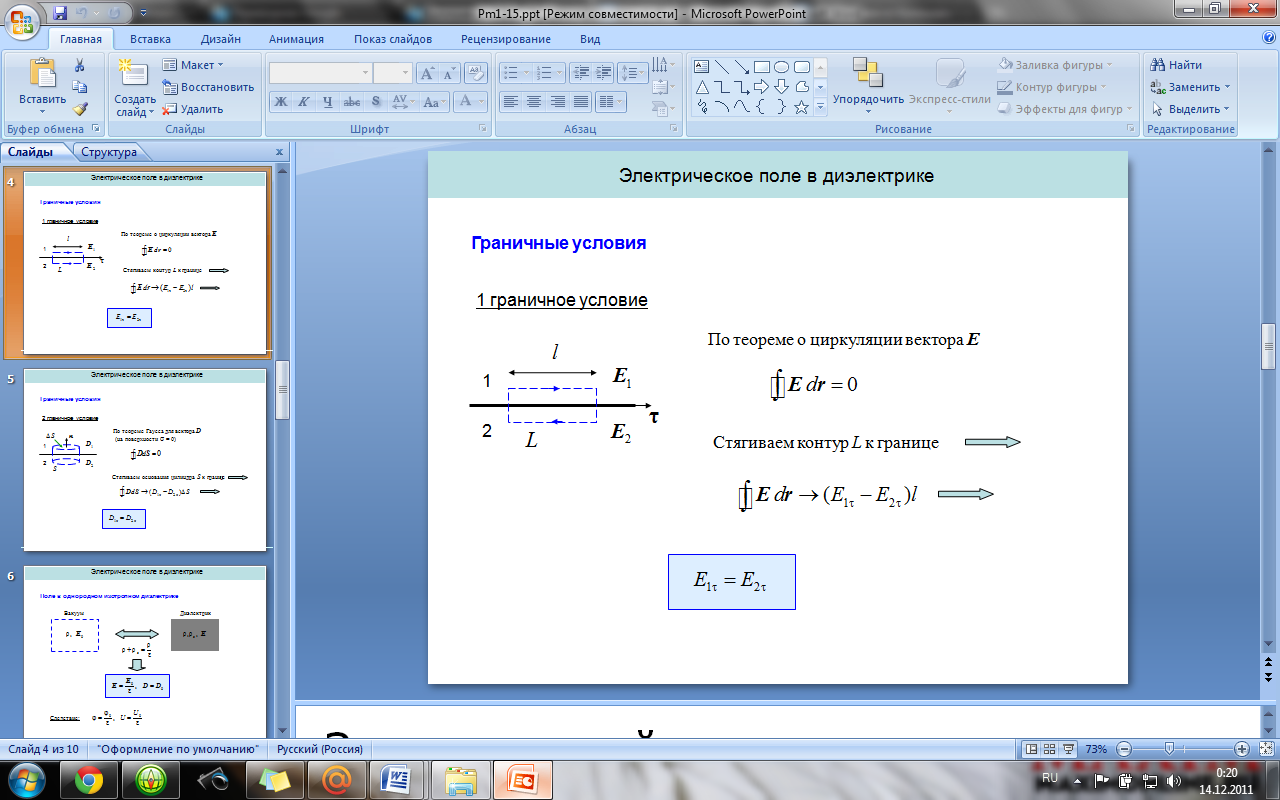
2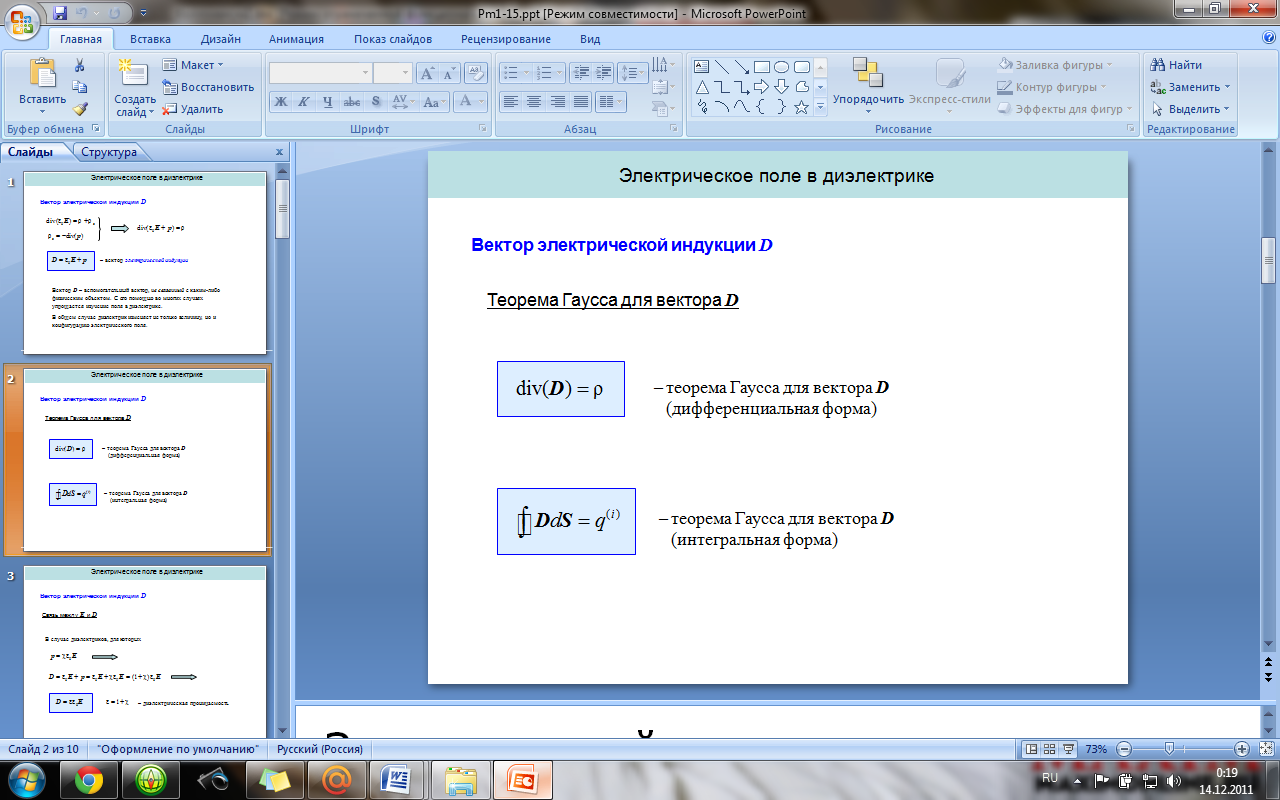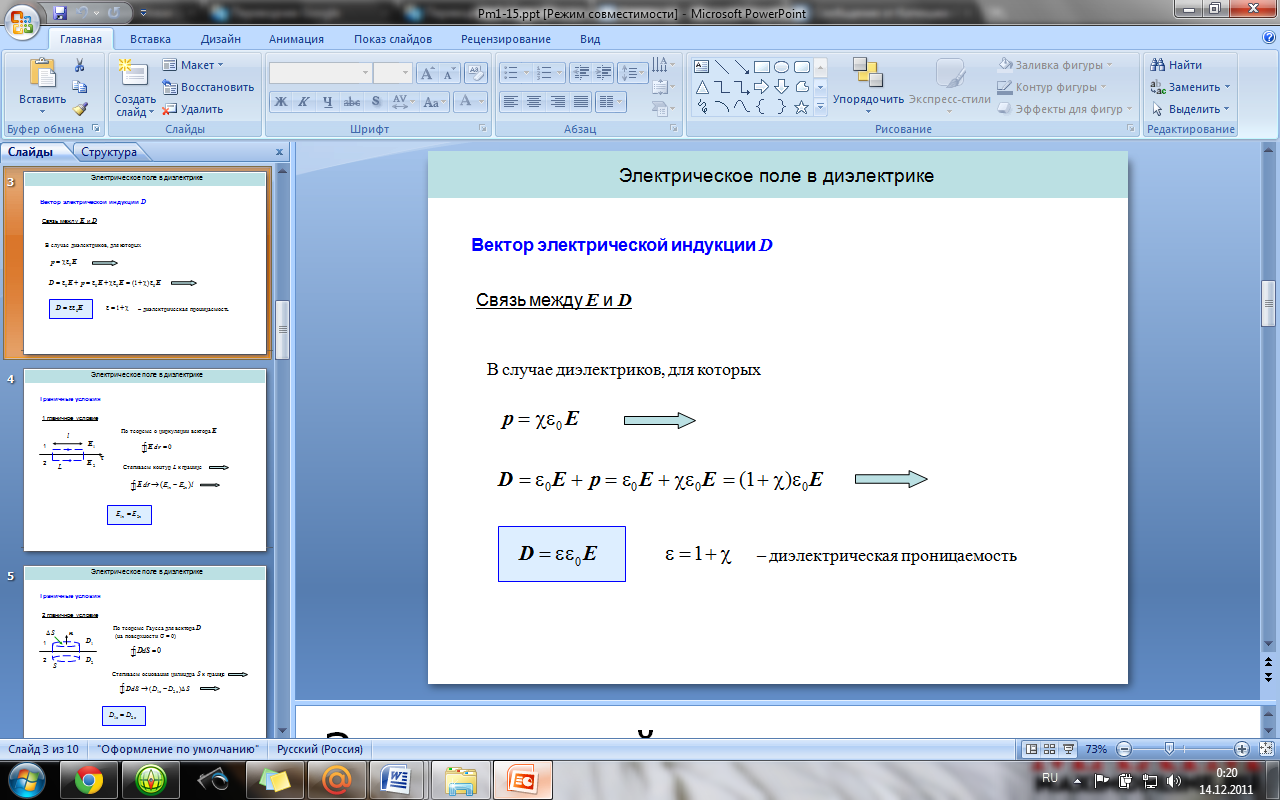6. Вектор электрической индукции. Теорема Гаусса для вектора электрической индукции (в интегральной и дифференциальной формах). Граничные условия на границе раздела двух диэлектриков.

2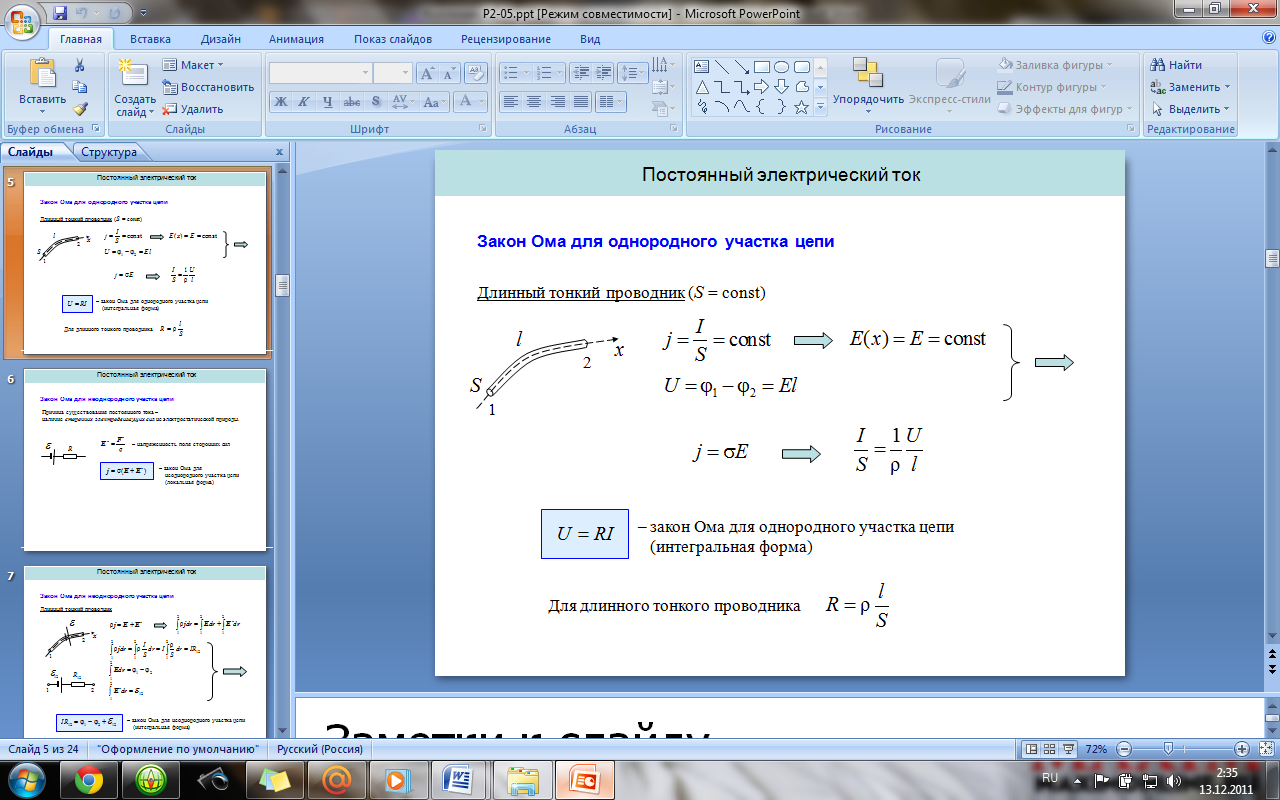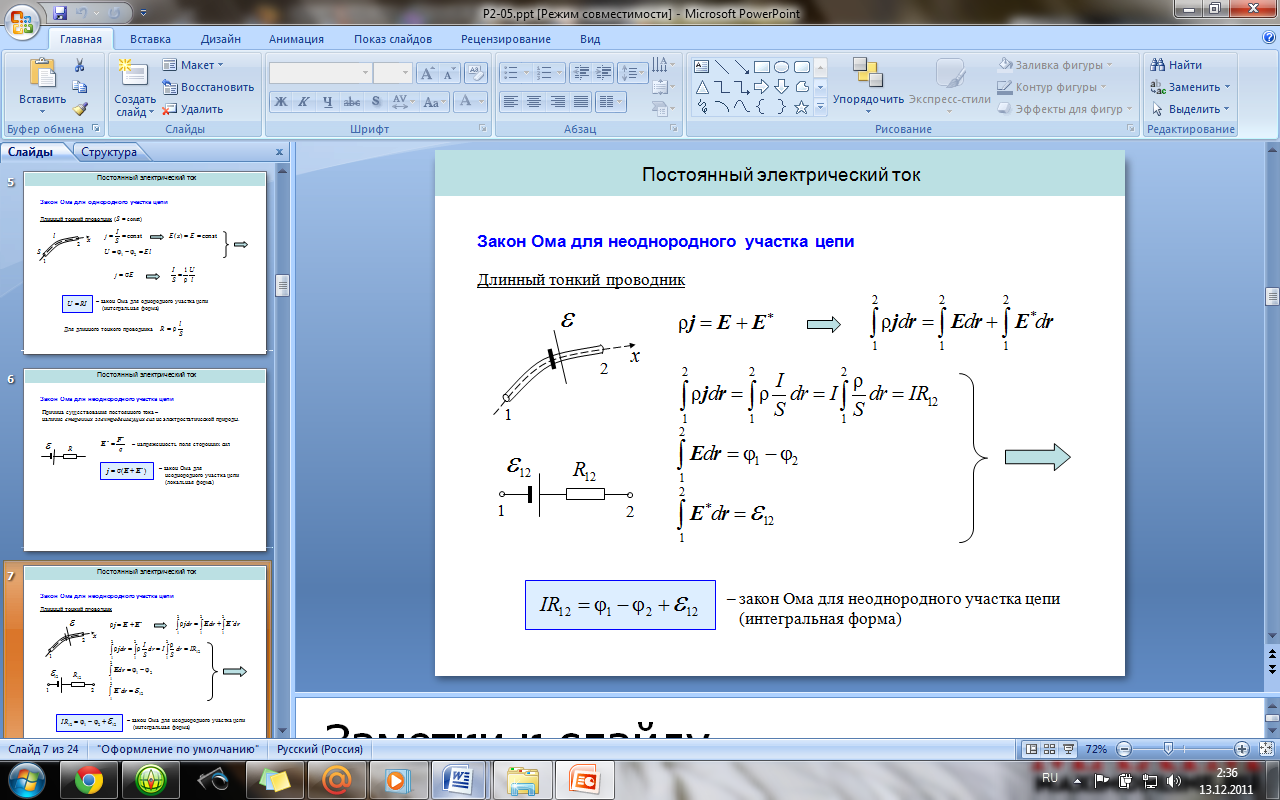8. Закон Ома для однородного и неоднородного участка цепи (в дифференциальной и интегральной формах).

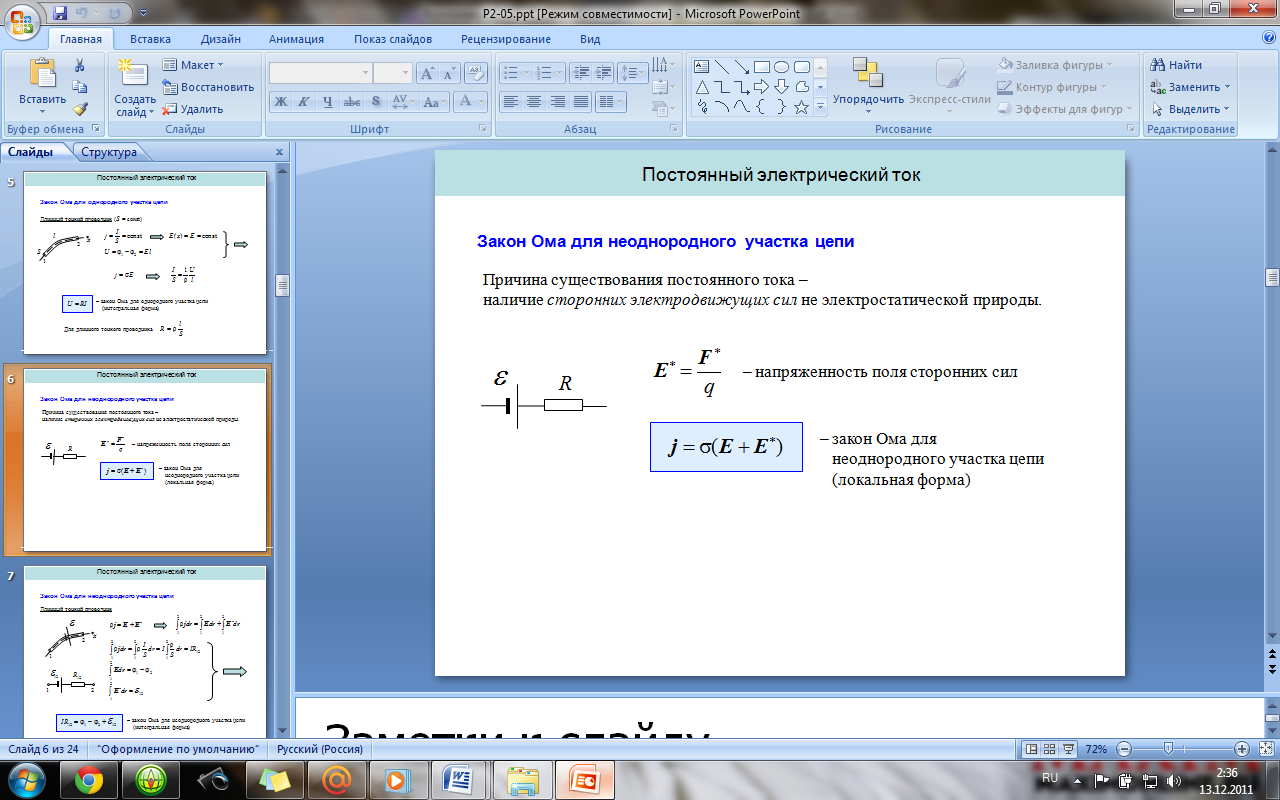
закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.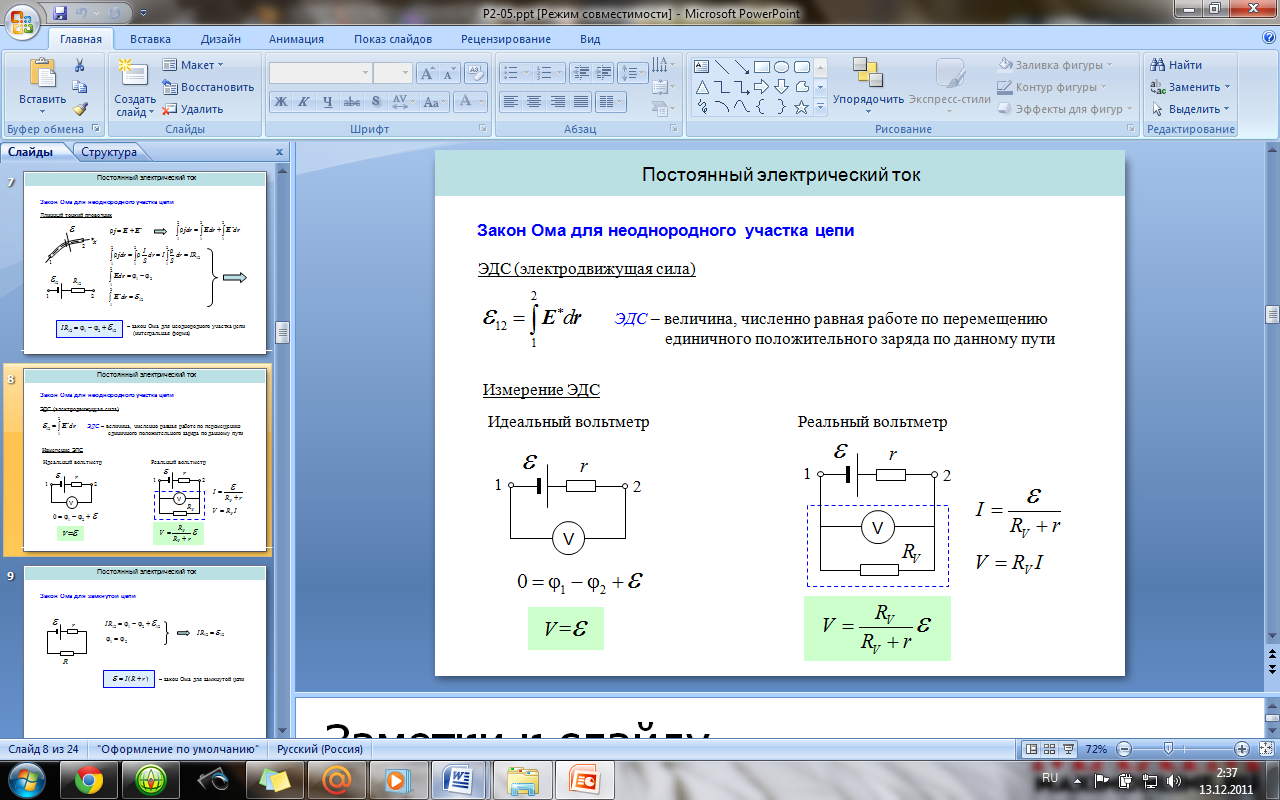

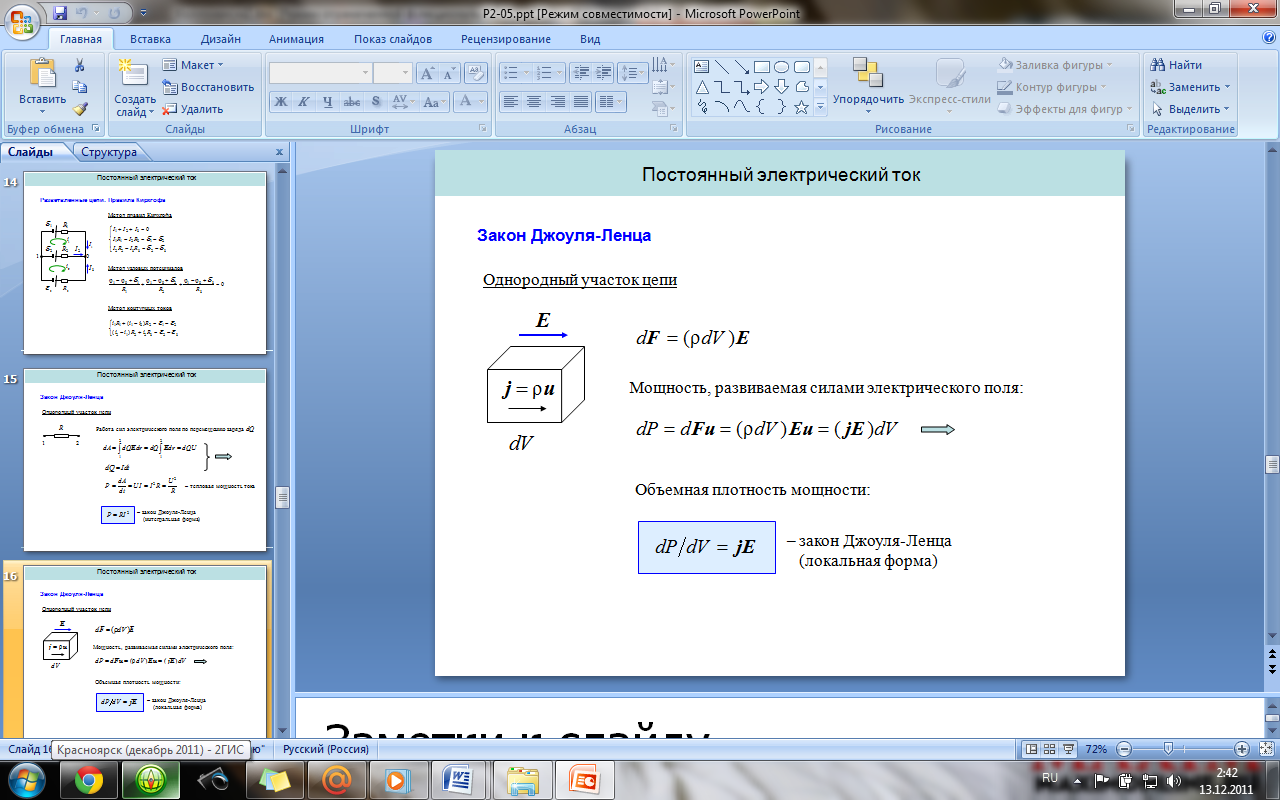
30. Работа сил электрического поля. Закон Джоуля-Ленца (в дифференциальной и интегральной формах).

При перемещении пробного заряда q в электрическом поле электрические силы совершают работу. Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.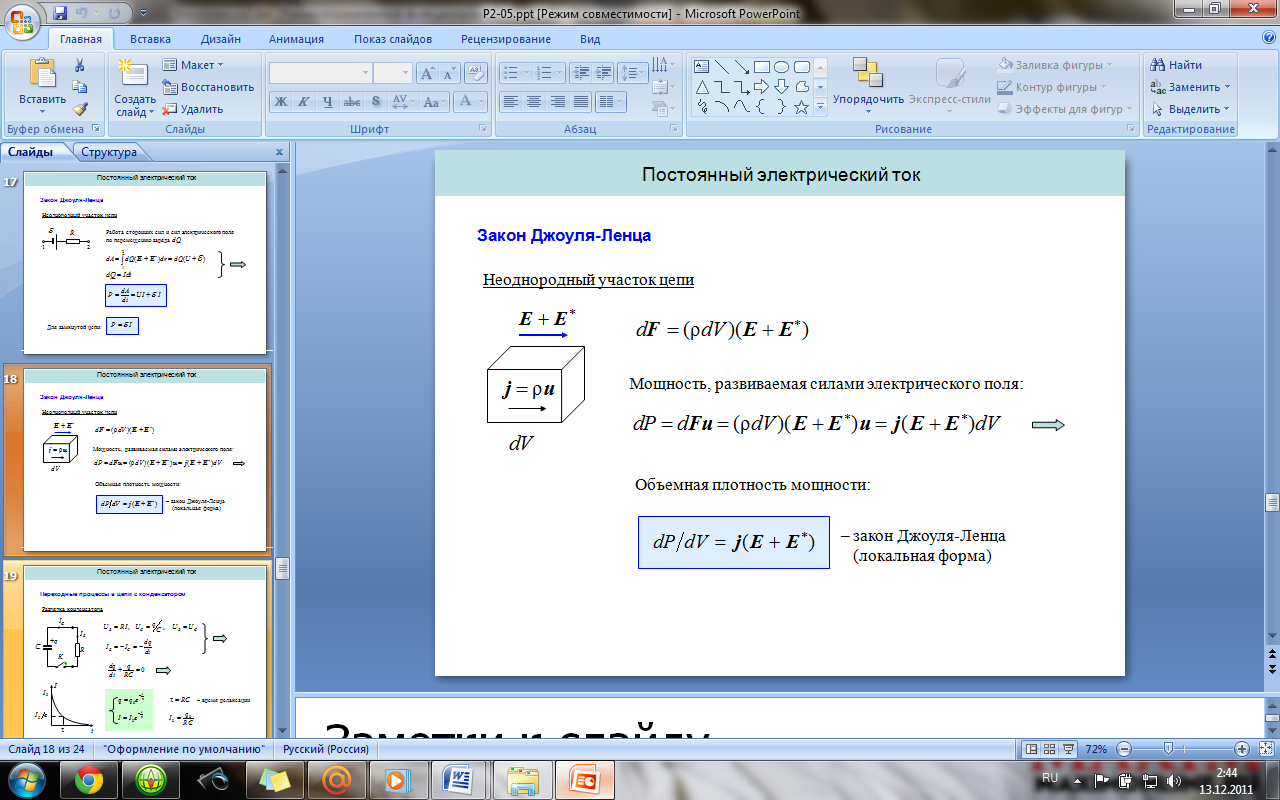

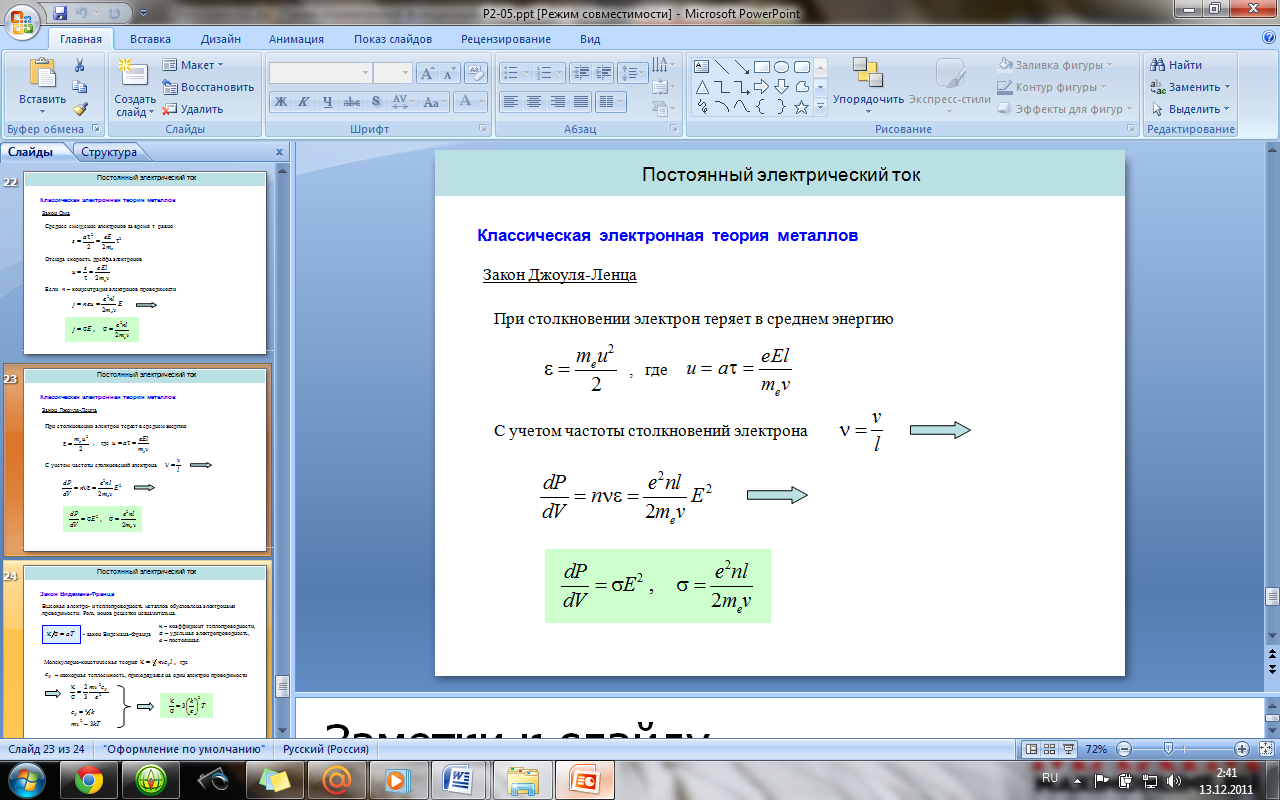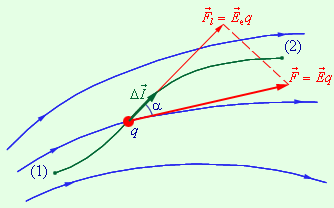
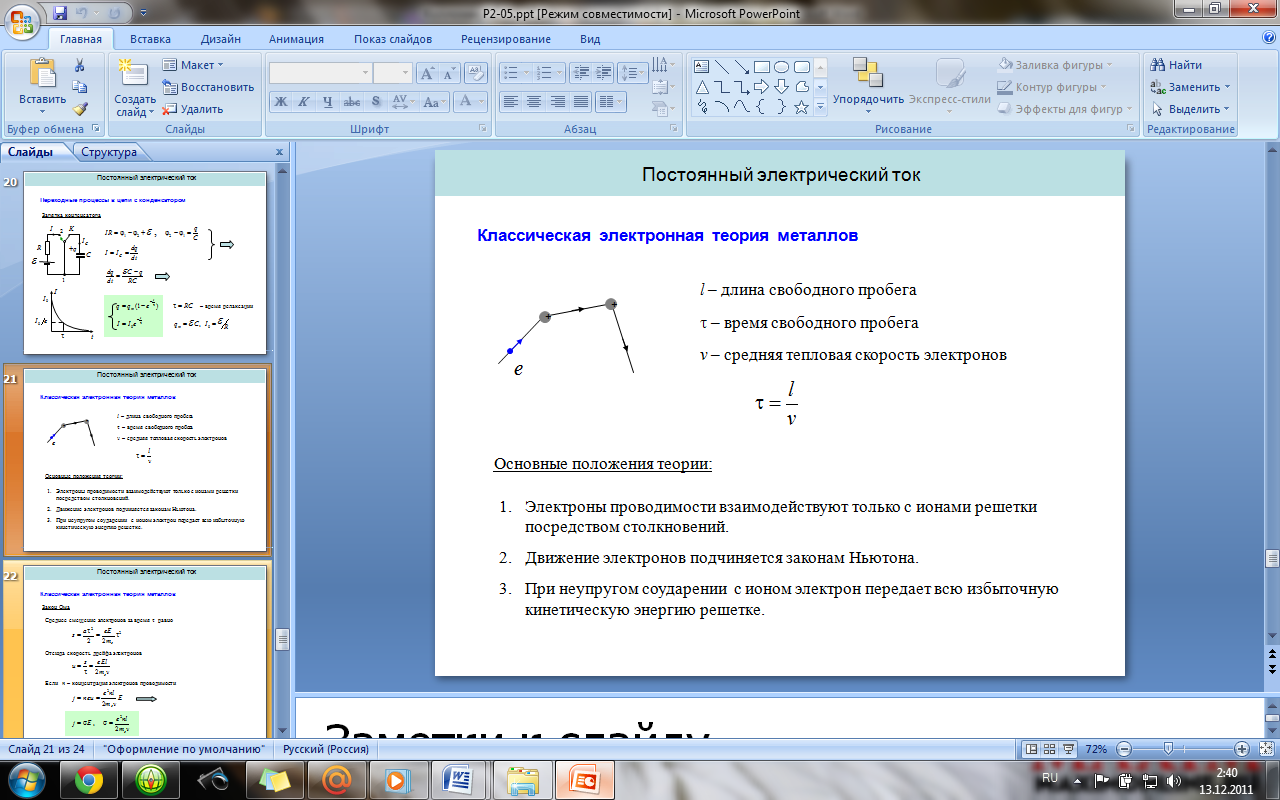
32. Классическая электронная теория металлов. Основные положения и обоснование законов Ома и Джоуля-Ленца. Затруднения теории.

3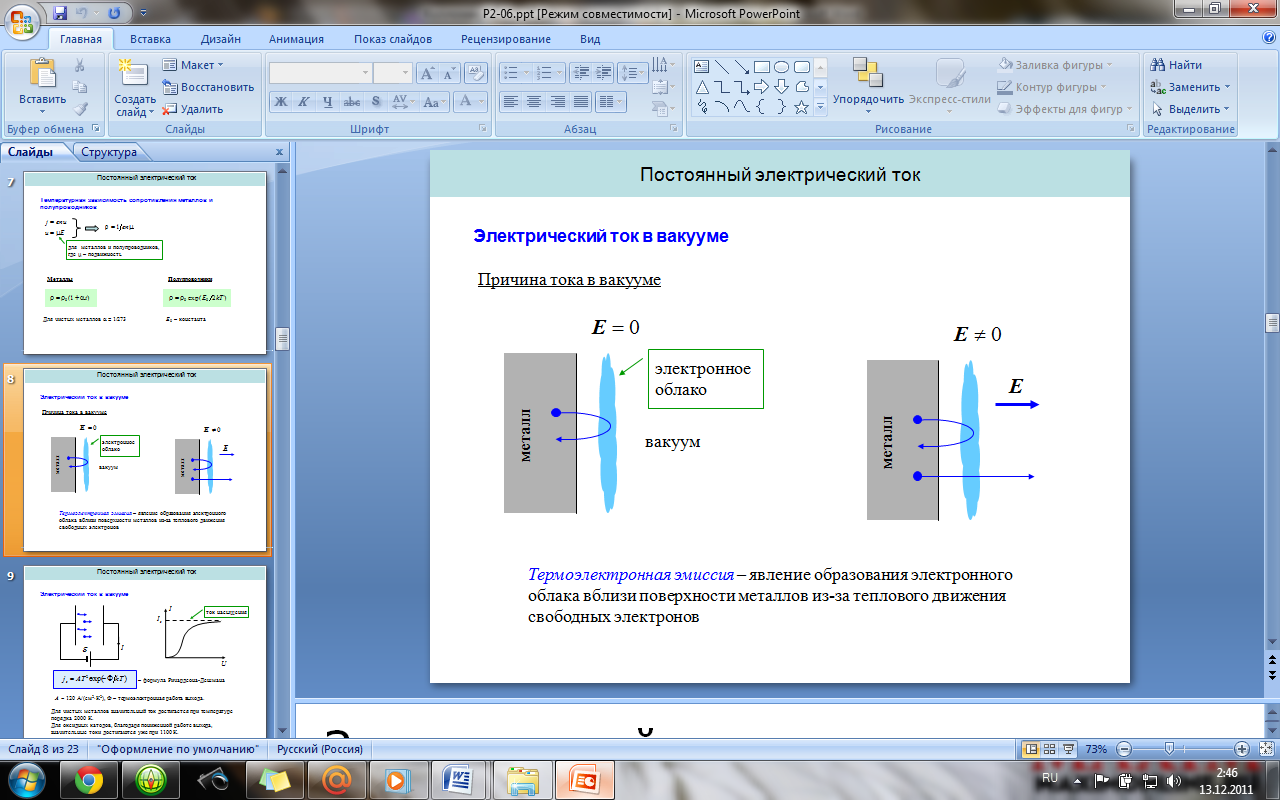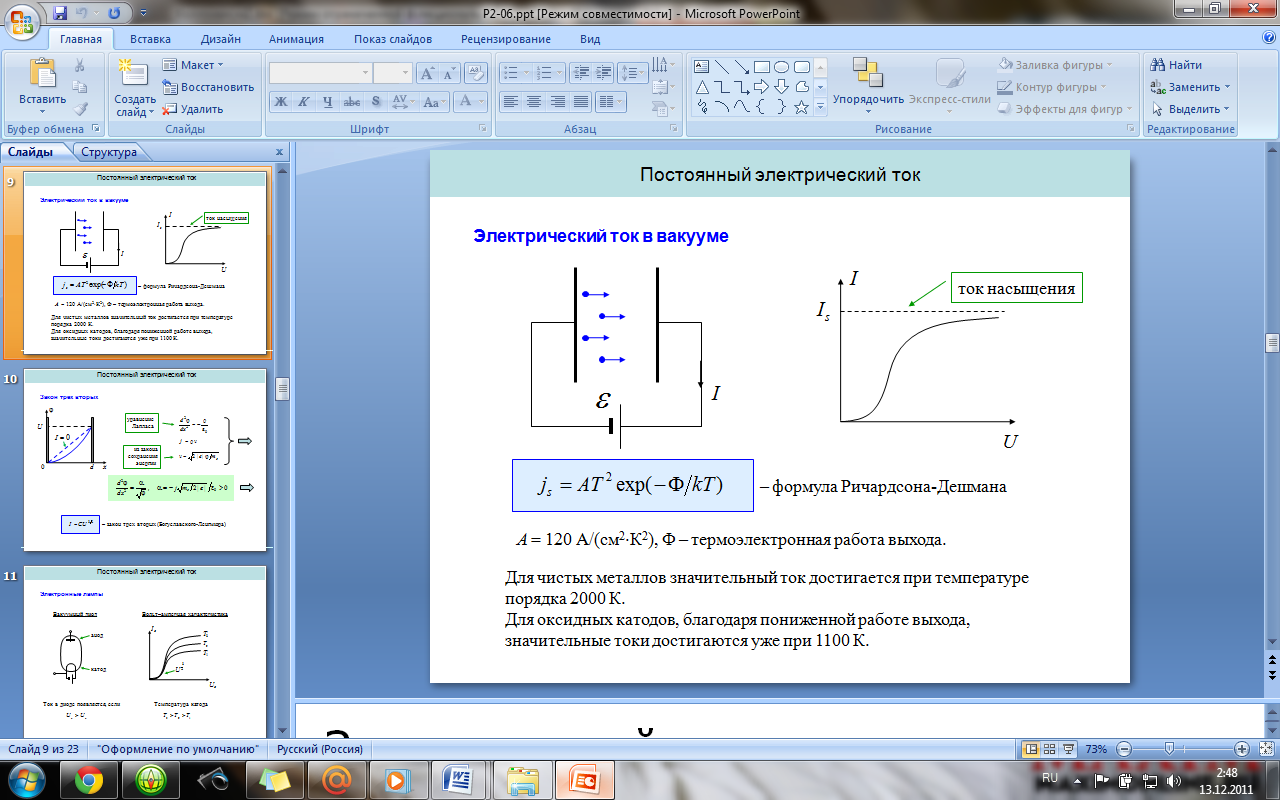4. Электрический ток в вакууме. Термоэлектронная эмиссия. Формула Ричардсона-Дешмана. Закон “трех вторых”.