1. Классы тестовых функций Класс одномерных унимодальных функций.

Покроем интервал [a,b] сеткой изMузлов и обозначим Ф(x_i)=Фi,.

Положим, что необходимо построить одномерную унимодальную функцию, минимум которой находится в узле , т.е. в точкеx_i^*.Тогда для генерации такой функций может быть использован следующий алгоритм построения тестовых одномерных унимодальных функций.

1. Генерируем дискретную случайную величину i^*, равномерно распределенную на множестве 1,2,…,M.

2. Генерируем случайные числа Ф_iпо рекуррентной формуле:

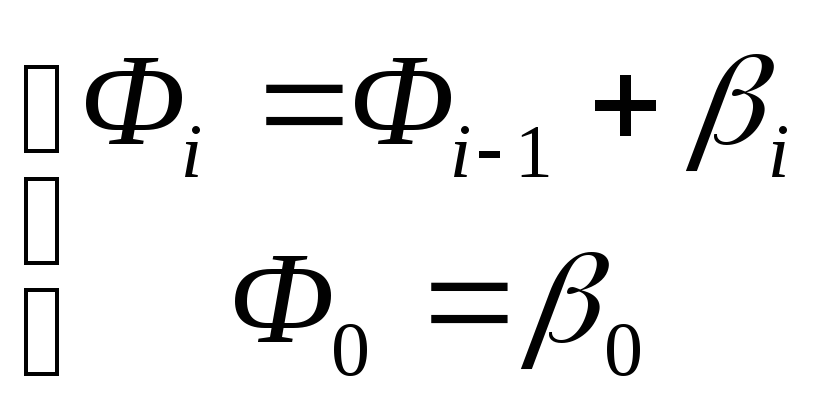, где β_i,- случайные величины, равномерно распределенные в интервале (-α,0), еслиi≤i^*, и в интервале (α,0), еслиi>i^*. Здесь α ‑ некоторая константа, определяющая максимальную скорость изменения искомой функции.

3. Для получения функции Ф(x) используем линейную интерполяцию полученных значений Ф_i,. Минимум полученной функции Ф(x) достигается в точкеx_i^*=x^*.

Функцию данного класса можно описать следующим образом:

,

где k₁иk₂– некоторые случайные величины.

Класс многоэкстремальных функций нескольких переменных.

Алгоритм генерации многоэкстремальных функций нескольких переменныхможно построить на основе использования совокупностиMквадратичных функций, каждая из которых дает локальный минимум искомой функции:, гдеквадратичная функция.

Здесь n– размерностьX,– точкаj-го локального минимума глубинойc_j, постоянные, , , c_j - случайные величины с некоторыми законами распределения.

5. Анализ результатов

Тестирование будем производить на одномерной унимодальной функции мультиверсиями, которые реализуют:

• метод дихотомии;

• метод «золотого сечения»;

• метод квадратичной интерполяции.

А также на функции Розенброка и классе многоэкстремальных функций несколько переменных программными реализациями алгоритмов:

• алгоритм Гаусса-Зейделя;

• алгоритм Нелдера-Мида;

• алгоритм Хука-Дживса;

• алгоритм Флетчера-Ривса.

При тестировании не имеет существенного значения то, какие именно алгоритмы оптимизации используются. Цель эксперимента - показать эффект от применения мультиверсионного программирования в системах управления. Поэтому важно лишь различие программных реализаций и различие конечного алгоритма функционирования.

Стандартные алгоритмы мультиверсионного голосования во всех исследуемых ситуациях показали заметно худшие результаты и по времени, и по отклонению от точки экстремума, чем метод голосования по значению оптимизируемой функции (см. главу 3). Результаты будем приводить только для этого метода согласования.

Так как, в случае сравнения мультиверсионной системы из нескольких методов, с каждым отдельным методом количество итераций основного цикла не может являться показателем производительности, то в таблицу результатов был добавлен показатель «время». Это число показывает время затраченное системой на весь процесс оптимизации. В случае с мультиверсионной системой, это время также включает время работы внутренних алгоритмов системы.

Показатель количества побед как мультиверсия отображает, какой вклад внес тот или иной модуль, в общий результат мультиверсионной системы.

Результаты представлены в таблице 3 .3.

В целом мультиверсионный подход к оптимизационным алгоритмам показывает не худшие результаты, чем наилучший из алгоритмов.

Таблица 3.3 Результаты исследования эффективности мультиверсионного подхода к алгоритмам оптимизации функций

Класс функций	Алгоритм	Время, по отн. к лучшему по времени	Время, по отн. к лучшему по результату	Среднее отклонение от точки экстремума	Побед как мультиверсия
Класс одномерных унимодальных функций	Мультиверсионная система	35,71	1,00	1,00	–
	Метод квадратичной интерполяции	24,86	0,70	0,97	0,85
	Метод «золотого сечения»	1,00	0,03	0,49	0,53
	Метод дихотомии	1,15	0,03	0,49	0,46
Функция Розенброка	Мультиверсионная система	1,93	1,00	0,96		–
	Метод Нелдера-Мида (версия 2)	1,02	0,53	1,05		0,76
	Метод Нелдера-Мида (версия 1)	1,00	0,52	22,74		0,71
	Метод Хука-Дживса (версия 1)	9,32	4,83	137,67		0,63
	Метод Гаусса-Зейделя	0,04	0,02	9801,82		0,85
	Метод Хука-Дживса (версия 2)	35,80	18,55	12461,90		0,48
	Метод Флетчера-Ривса (версия 1)	130,03	67,37	32156,17		0,92
	Метод Флетчера-Ривса (версия 2)	86,60	44,86	37708,33		0,88
Класс многоэкстремальных функций нескольких переменных	Мультиверсионная система	2,76	1,00	6,17	–
	Метод Флетчера-Ривса (версия 1)	1,47	0,53	6,20	0,93
	Метод Флетчера-Ривса (версия 2)	1,48	0,53	7,07	0,90
	Метод Нелдера-Мида (версия 1)	1,23	0,45	312,63	0,25
	Метод Нелдера-Мида (версия 2)	1,00	0,36	616,78	0,41
	Метод Хука-Дживса (версия 2)	159,42	57,75	735,10	0,63
	Метод Хука-Дживса (версия 1)	165,12	59,81	1069,42	0,64
	Метод Гаусса-Зейделя	58,62	21,23	8514,35	0,36