
2012_Topology / L-KoGom
.pdf
∆ Кратное интегрирование. Когомологии |
41 |
Это означает, что какое-то разбиение единицы мы уже имеем. Но требуется, чтобы разбиение было подчинено покрытию Ui. Определим теперь
ψi ≡ |
k:rX(k |
′. |
ψk |
||
|
)=i |
|
Это и есть искомое семейство функций. В самом деле,
X |
Xk:rX(k |
X |
ψi = |
ψk |
′ ≡ ψk′ ≡ 1. |
i |
i )=i |
k |
Носитель |
|
|
[
supp ψi supp (ψk′) Ui
k:r(k)=i
по построению, а свойство 3) следует из локальной конечности покрытия
{Hk}. Теорема доказана.
Заметим, что для каждого фиксированного k выбирается только однo
Hk Ui, чтобы не посчитать одну функцию дважды при разбиении суммы ряда в сумму порядков ψi. Само Hk может вписаться во много Ui, но мы ему ставим в соответствие определенный i определенным образом. Этот момент говорит о том, что разбиение единицы можно строить по-разному, в зависимости от того, как выбрали отображение r.
4. Теорема Сарда
Пусть X и Y — гладкие многообразия размерностей n и k соответственно. Рассмотрим отображение F : X → Y класса C1.
Определение 3.2. Точка x0 X — регулярная точка отображения F , если в локальных координатах матрица Якоби отображения F имеет в точке x0 максимальный ранг (т.е. min (n, k)). Если точка x0 не является регулярной, она называется критической точкой.
Определение 3.3. Точка y0 Y называется критическим значением
отображения F , если ее прообраз F −l(y0) содержит критическую точку; в противном случае y0 называется регулярным значением.

42 |
И.А. Антипова, О.В. Знаменская, А.К. Цих ∆ |
Определение 3.4. Говорят, что подмножество A в Rn является множеством меры нуль, если ε > 0 его можно погрузить в объединение счетного числа кубов общего объема, не больше, чем ε.
Определение 3.5. Подмножество A многообразия Y имеет меру 0, если существует покрытие многообразия Y счетным множеством карт ϕi :
Ui → Rn, Для которого каждое множество ϕ(X ∩ U) Rn имеет меру
нуль.
Теорема 3.2 (Теорема Сарда). Если отображение F C1 ∩ Cn−k+1, то множество его критических значений имеет меру нуль в Y .
Доказательство теоремы Сарда в приведенной выше общей формулировке не просто, и мы не будем его здесь приводить (см. [Прасолов]).
Рассмотрим случай, когда F C1 и n = k. В этом случае точка x0 X
является критической для отображения F : X → Y , если якобиан ∂(F ) в
∂(x)
точке x0 равен нулю.
Теорема 3.3. Пусть X и Y многообразия размерности n и F : X → Y
— отображение класса C1. Тогда множество критических значений F
имеет меру нуль в Y .
Доказательство. Достаточно рассматривать F на некотором замкнутом кубе C0 в Rn со стороной l. Разобьем этот куб на Nn равных частей (кубиков), поделив каждое ребро на N равных частей. Тогда для любой пары точек x0, x лежащих в одном из кубиков C
F (x) = F (x0) + ∂x |
(x0)(x − x0) + o |
n |
, |
||
|
∂F |
|
1 |
|
|
поскольку первые производные отображения F равномерно непрерывны в
C0. Если x0 является критической точкой, то det ∂F∂x (x0) = 0 и поэтому образ кубика C содержится в цилиндре, основание которого лежит в
(n−1)-мерной плоскости и имеет площадь 6 c(l/N)(n−1), а высота 6 o(l/N), где c — некоторая положительная константа. Поскольку число кубиков, содержащих критические точки, не больше, чем Nn, то при отображении F

∆ Кратное интегрирование. Когомологии |
43 |
их образы все лежат в некотором множестве, объем которого не превосходит Nno(l/Nn). Устремляя N к ∞, получаем требуемый результат. 

44 |
И.А. Антипова, О.В. Знаменская, А.К. Цих ∆ |
Лекция 4 ´
Отображения многообразий, их дифференциалы и касательные пространства
Отображения многообразий. Касательные векторы, касательные пространства и дифференциалы отображений. Касательное расслоение и векторные поля.
1. Отображение многообразий
Определим на многообразии функции так, чтобы это задание было инвариантно относительно преобразования координат при переходе из одной локальной карты в другую.
Пусть X — произвольное вещественное n-мерное многообразие.
Определение 4.1. Говорят, что на многообразии X задана функция f :
X → R, если в каждой окрестности Uα X задана функция
f Uα = fα(xα)
локального параметра x(α) Uα. При этом, если Uα ∩ Uβ ̸= , то
fα(xα) = fβ ◦ ϕαβ(x(α)).
Итак, функция f на n-мерном многообразии в локальных координатах есть функция n действительных переменных, следовательно, локально мы можем определять на X функции разных классов гладкости C. Однако класс гладкости, которому принадлежит функция, определенная глобально, очевидно, зависит от класса гладкости многообразия, т.е. соотношений соседства ϕαβ. Действительно, если какое-либо соотношение соседства не дифференцируемо, то и функция при переходе к локальной карте может оказаться недифференцируемой.
Заметим, что функция — частный случай отображения многообразия
X в Y (когда Y = R). Не трудно обобщить определение 4.1 на случай произвольных отображений.
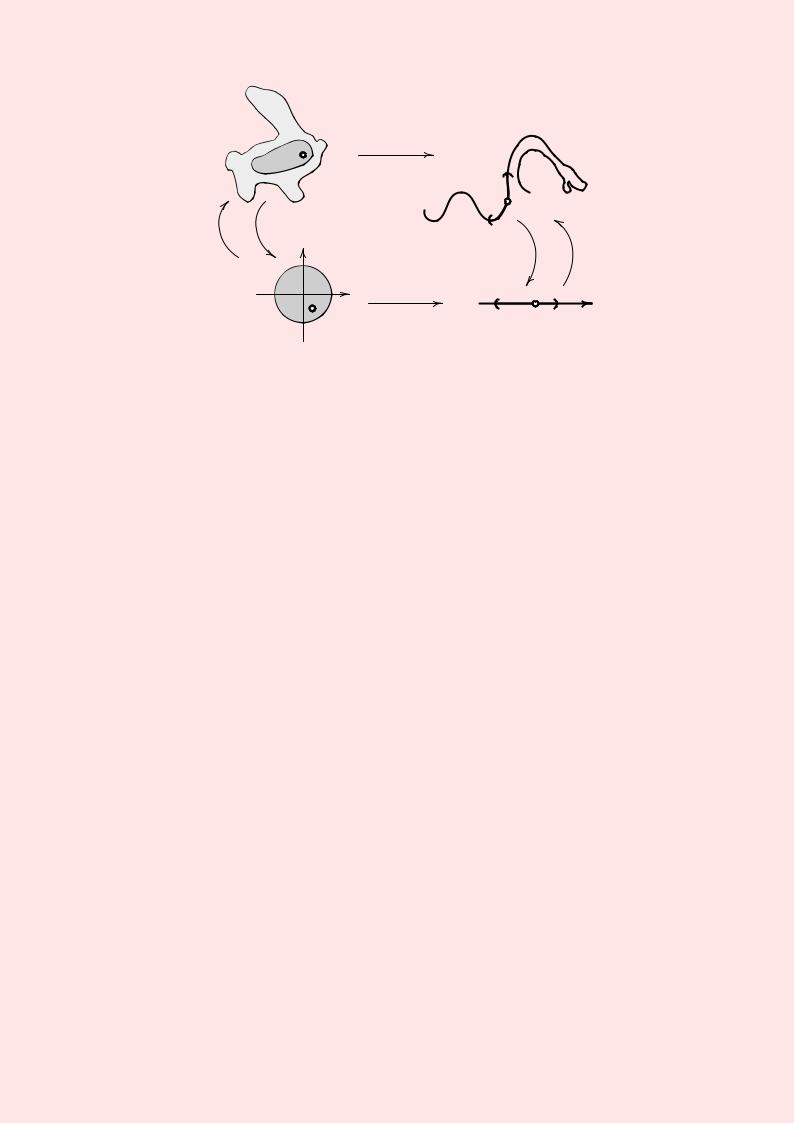
∆ Кратное интегрирование. Когомологии |
45 |
X |
f : X → Y |
Y |
|
|
|
|
P |
|
|
f(P ) |
|
ϕ−1 ϕ |
ψ |
ψ−1 |
|
||
|
ψ ◦ f ◦ ϕ−1 |
|
Rxn |
ϕ(P ) |
Rym |
Отображение многообразий
Пусть X — многообразие размерности n с атласом {Uα, ϕα} и Y —
многообразие размерности m с атласом {Vβ, ψβ}. Рассмотрим отображение многообразий f : X → Y . Оно индуцирует отображение координатных окрестностей Uα и Vβ:
ψβ ◦ f ◦ ϕ−α 1(x) : ϕ−α 1 Uα ∩ f−1(Vβ) Rmx −→ Rny .
Если многообразия X, Y были класса C, а ψ ◦ f ◦ ϕ−1 : Rnx −→ Rmy для любой координатной окрестности принадлежит классу C′ C, то f C. Т. о. f : X → Y — гладкое отображение, если y = ψ ◦ f ◦ ϕ−1(x) : Rmx → Rny
— отображение класса C∞ для любой координатной окрестности U X. Далее будем рассматривать только гладкие многообразия и их гладкие
отображения.
2. Три определения касательного вектора
Координатное определение касательного вектора. Пусть X — гладкое вещественное многообразие размерности n.
Касательный вектор в точке p X легко определить в локальной системе координат, но при переходе к другой системе координат возникают некоторые трудности. Поэтому используется несколько определений касательного вектора, которые бывают полезны в разных ситуациях.
Одно из наиболее естественных определений таково. Касательный вектор в точке p X — это некий объект, которому в каждой локальной си-

46 |
И.А. Антипова, О.В. Знаменская, А.К. Цих ∆ |
стеме координат (U, ϕ) с началом в точке p (т.е. с условием ϕ(p) = 0 Rnx) соответствует определенный вектор v = (v1, . . . , vn) Rnx; при этом в локальной системе координат (V, ψ) тому же самому касательному вектору соответствует вектор w = (w1, . . . , wn) Rny , где
w |
|
= |
∂(ψ ◦ ϕ−1)i |
(0) vj. |
(4.1) |
|
i |
Xj |
∂xj |
|
|
Здесь (ψ ◦ ϕ−1)i обозначает i-ую координату отображения перехода x → y = (ψ ◦ ϕ−1)(x).
Иными словами, w — образ вектора v под действием матрицы Якоби отображения перехода ψ ◦ϕ−1. Корректность этого определения следует из того, что матрица Якоби композиции двух отображений является произве-
дением матриц Якоби этих отображений.
Основной недостаток этого определения — зависимость от выбора системы координат. Чтобы получить инвариантное определение, можно по-
ступить разными способами.
Касательный вектор как класс эквивалентных кривых. Известно, что
для гладких кривых x = x(t) в пространстве Rn касательный вектор в точке x0 = x(t0) выражается вектором скорости x′(t). Если Rn мыслить как пространство локальных координат карты (U, ϕ) многообразия X, то всякую кривую x(t) можно поднять на X в виде γ(t) = ϕ−1 x(t) .
Для удобства предположим, что x(0) = 0 и что (U, ϕ) — локальная
система координат с началом в точке p X, т.е. что ϕ(p) = 0. В таком случае γ(0) = p.
Касательный вектор в точке p X можно определить как класс эквивалентности гладких кривых γ : R → X, для которых γ(0) = p. Кривые γ1
и γ2 считаются эквивалентными, если для некоторой системы координат
(U, ϕ) с началом в точке p выполняется равенство
d(ϕ ◦dt |
1( )) t=0 = |
( |
ϕ |
◦dt |
2( )) t=0. |
||
γ |
t |
|
d |
γ |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

∆ Кратное интегрирование. Когомологии |
47 |
Если (V, ψ) — другая система координат с началом в точке p, то
d(ψ ◦ γ(t))i
dt t=0
= d(ψ ◦ ϕ−1ϕ ◦ γ(t))i
dt t=0
= |
∂(ψ ◦ ϕ−1)i (0)d(ϕ ◦ γ(t))j . |
||
j |
∂xi |
dt |
t=0 |
X |
|
|
|
Поэтому, во-первых, эквивалентность кривых не зависит от выбора локальных координат, а во-вторых, вектор
d(ϕ ◦ γ(t)) v =
dt t=0
при переходе к другой системе координат преобразуются по закону (4.1). Таким образом, вектор скорости для представителя γ класса [γ] и пред-
ставляет касательный вектор в смысле определения пункта 1.
Касательный вектор как оператор дифференцирования. Оказывается, геометрические свойства многообразий можно получать, изучая класс всех гладких функций на них. В частности, на языке функций, заданных на многообразии (или в как угодно малых окрестностях), можно получить описание касательных векторов к многообразиям.
Итак, пусть (U, ϕ) — локальная система координат с началом в точке p X, v Rn и f : Up → R — гладкая функция, определенная в некоторой окрестности Up точки p. Функции f сопоставим число
X ∂(f ◦ ϕ−1)(0)vi,
i∂xi
равное значению производной функции fϕ−1(x) (т.е. производной функции f в локальных координатах x в направлении вектора v). При переходе к другой системе координат (V, ψ) вектор v заменится на вектор w с координатами
wi = X ∂(ψ ◦ ϕ−1)i (0)vj,
j ∂xj
поэтому функции f в новой системе координат будет сопоставлено число
|
∂ |
f ◦ ψ−1 |
|
(0)w |
|
= |
|
∂(f ◦ ψ−1) |
(0) |
∂(ψ ◦ ϕ−1)i |
(0)v |
. |
i |
|
∂yi |
|
|
i |
|
i,j |
∂yi |
∂xj |
j |
|
|
X |
|
|
|
|
|
|
X |
|
|
|
|
|

48 |
И.А. Антипова, О.В. Знаменская, А.К. Цих ∆ |
При фиксированном j сумму по i в правой части равенства можно интерпретировать как производную по xj сложной функции f ◦ ψ−1 ◦ ψ ◦ ϕ−1 = f ◦ ϕ−1, поэтому получаем
|
∂ |
f ◦ ψ−1 |
|
(0)w |
|
= |
|
∂(f ◦ ϕ−1) |
(0)v |
. |
i |
|
∂yi |
|
|
i |
|
j |
∂xj |
j |
|
X |
|
|
|
|
|
|
X |
|
|
|
Таким образом, число, сопоставляемое функции f, не зависит от выбора системы координат.
Касательному вектору v в точке p X мы сопоставили линейный оператор v : C∞(X) → R (вместо C∞(X) можно взять C∞(U) где U —
некоторая окрестность точки p, поскольку число v(f) зависит только от поведения функции f в сколь угодно малой окрестности точки p). При этом выполняются следующие свойства:
1)(λv + µw)(f) = λv(f) + µw(f);
2)v(fg) = f(p)v(g) + g(p)v(f).
Второе свойство следует из правила Лейбница
∂(fg) = g ∂f + f ∂g . ∂xi ∂xi ∂xi
Свойства 1) и 2) вместе с линейностью оператора v можно взять за определение линейного пространства касательных векторов в точке p X. Но при этом нужно проверить, что не появится "лишних" операторов, т.е. если v : C∞(Rn) → R — линейный оператор, обладающий свойством
v(fg) = f(0)v(g) + g(0)v(f),
то
v(f) = Xi |
∂f |
(0)vi |
|
||
∂xi |
для некоторого v = (v1, . . . , vn) Rn. Для этого нам понадобится следующее вспомогательное утверждение.

∆ Кратное интегрирование. Когомологии |
49 |
Лемма 4.1. Пусть f C∞(U), где U Rn — выпуклая окрестность начала координат, и f(0) = 0. Тогда существуют такие функции
g1, . . . , gn C∞(U), что f(x) = Pxigi(x) и gi(0) = ∂f (0).
∂xi
Доказательство. В силу выпуклости U для каждого x U отрезок, соединяющий x с началом координат, также принадлежит U, поэтому по формуле Ньютона-Лейбница и правилу дифференцирования сложной функции имеем
1 |
dt |
1 |
n |
|
|
dt. |
f(x) = f(x) − f(0) = Z |
dt = Z |
i=1 xi ∂xi |
||||
|
df(tx) |
|
X |
∂f(tx) |
|
|
0 |
|
0 |
|
|
|
|
В качестве искомых функций gi(x) положим
1 |
∂xi |
dt. |
gi(x) = Z0 |
||
|
∂f(tx) |
|
Если смотреть на последний интеграл, как на интеграл с параметром x, то мы видим,что подынтегральное выражение непрерывно по совокупности переменных x и t и принадлежит классу C∞(U) по x при каждом значении t [0, 1]. По известной теореме из анализа заключаем, что gi C∞(U). При этом
1 |
∂xi |
(0)dt = |
∂xi |
(0). |
gi(0) = Z0 |
||||
|
∂f |
|
∂f |
|
Из леммы 4.1 требуемое утверждение следует очевидным образом. Дей-
ствительно, f(x) − f(0) = Pi |
xigi(x), поэтому |
|
|
||
v(f) = Xi |
0 · v(gi) + Xi |
gi(0)v(xi) = Xi |
∂f |
(0)vi, |
|
∂xi |
|||||
где vi = v(xi).
Касательные векторы в точке p X образуют линейное пространство размерности n, если размерность многообразия равна n. Это пространство называют касательным пространством в точке p и обозначают TpX.
3. Дифференциал отображения

50 И.А. Антипова, О.В. Знаменская, А.К. Цих ∆
Пусть f : X → Y — гладкое отображение гладких многообразий.
Для каждой точки p X отображению f ставится в соответствие ли-
нейный оператор
(df)p : TpX −→ Tf(p)Y
из касательного пространства TpX в касательное пространство Tf(p)Y . Этот оператор называется дифференциалом отображения f или производным отображением для f. Его также обозначают просто df, если понятно, о
какой точке p идет речь.
Опишем это соответствие для каждой из приведенных выше интерпре-
таций касательных векторов.
Пусть касательный вектор v TX задан координатами (v1, . . . , vn), при-
писанными локальной |
системе координат (Uϕ) |
на X. Тогда его образ |
|||||
w = df(v) Tf(p)Y |
в локальной системе координат (Vψ) есть результат |
||||||
действия на v матрицы Якоби отображения f: |
|
||||||
w = ∂(ϕ−∂(◦x) ◦ |
ψ |
) x=0(v) |
(мы полагаем, что ϕ(p) = 0). |
||||
1 |
f |
|
|
|
|||
|
|
|
|
|
|
|
|
Если вектор v |
задан |
кривой |
γ(t), то вектор |
df(v) задается кривой |
|||
f(γ(t)). А если вектор v задан как линейный оператор на гладких функциях, то вектор df(v) задается как оператор df(v)(g) = v(g ◦ f), где g C∞(Uf(p)).
Условие, что f — иммерсия (субмерсия) в точке p эквивалентно тому, что дифференциал отображения f в точке p — мономорфное (эпиморфное) отображение. В такой форме иногда бывает удобнее проверять, что f —
иммерсия (субмерсия).
4. Касательное расслоение и векторные поля
На множестве
[
TX = TpX
p X
можно ввести структуру многообразия следующим образом. Пусть (U, ϕ)
— локальная система координат на многообразии X. Сопоставим касательному вектору в точке p X пару (ϕ(p), v), где v = (v1, . . . , vn) — координа-
