
Diffgeomm / diffgeom-sbornik-zadach
.pdfДифференциальная геометрия и топология |
11 |
крытыми множествами N, и множества, дополнения до которых конечны.
Описать все непрерывные действительные функции на этом топологиче-
ском пространстве.
47.Какие множества прямой могут быть непрерывными образами множества M точек плоскости, у которых по крайней мере одна из координат рациональная?
48.Найти все непрерывные действительные функции, определённые на всей прямой, переводящие любое открытое множество в замкнутое.
49.Будем считать Землю идеально гладким шаром. Рассмотрим множество A всех точек x на поверхности Земли, которые обладают свойством: если из x пройти 10 км на север, затем 10 км на запад, и, наконец, 10 км на юг, то окажешься снова в точке x. Является ли множество A замкнутым?
12 |
О.В. Знаменская, В.В. Работин |
3.Компактные пространства
50.Доказать, что компактное пространство с дискретной топологией конечно.
51.Доказать, что пространство X компактно тогда и только тогда, когда каждое покрытие пространства X элементами некоторой базы содержит конечное подпокрытие.
52.Доказать, что пространство X компактно тогда и только тогда, когда любая система замкнутых в X множеств, таких, что пересечение любого их конечного числа не пусто, имеет непустое пересечение.
53.Доказать, что пространство X компактно тогда и только тогда, когда любая центрированная система произвольных в X множеств имеет точку прикосновения. (Семейство множеств называется центрированным, если пересечение любого конечного числа этих множеств не пусто.)
54.Доказать, что любое замкнутое подпространство компактного пространства компактно.
55.Доказать, что в каждом бесконечном компактном пространстве существует счетное незамкнутое множество.
56.Доказать, что любое компактное подпространство хаусдорфова пространства X является замкнутым в X множеством.
57.Доказать, что незамкнутое подпространство хаусдорфова пространства не является компактным пространством.
58.Доказать, что пересечение любого семейства замкнутых компактных множеств является замкнутым и компактным множеством.
59.Привести пример топологического пространства, в котором пересечение некоторых двух компактных множеств не является компактным множеством.
60.Привести пример топологического пространства, в котором замыкание некоторого компактного множества не компактно.
61.Пусть Y = {Aα : α M}, где каждое Aα — компактное подмножество в некотором хаусдорфовом пространстве и пересечение любого конеч-
Дифференциальная геометрия и топология |
13 |
ного семейства элементов из Y связно. Доказать, что множество |
Aa |
связно. |
α M |
S |
62.Доказать, что замкнутое подпространство компакта само является компактом.
63.Доказать, что всякий компакт замкнут в объемлющим его метрическом пространстве.
64.Привести пример замкнутого ограниченного
некомпактного подмножства в l2.
65.Привести пример замкнутого ограниченного, некомпактного подмножества в C[0, 1].
3.6. Связность
66.Привести пример связного не локально связного хаусдорфова компактного пространства.
67.Пусть X — связное хаусдорфово пространство, A и B — непустые непересекающиеся замкнутые в нем множества. Доказать, что существует компонента множества X \ (A B), замыкание которой пересекается с A и
B.
68.Доказать, что топологическое произведение любого семейства связных пространств связно.
69.Привести пример топологического пространства, содержащего одноточечные компоненты связности.
70.Доказать, что если A и B — замкнутые множества, объединение и пересечение которых являются связными множествами, то и множества A,
B — связные. Верно ли это утверждение для незамкнутых множеств A и
B?
71. Доказать, что замыкание связного множества связно.
3.7. Непрерывные отображения и гомеоморфизм
72.Доказать, что образ базы при непрерывном отображении может не
быть базой.
73.Доказать, что в Rn круговой цилиндр конечной высоты без основа-
14 |
О.В. Знаменская, В.В. Работин |
ний, однополостной гиперболоид, открытое кольцо и сфера без двух точек гомеоморфны друг другу.
74. Доказать, что любые два открытые выпуклые подмножества в Rn
гомеоморфны в индуцированной топологии. Справедливо ли это утверждение для любых замкнутых выпуклых подмножеств?
75.Указать негомеоморфные топологические пространства, каждое из которых гомеоморфно подпространству другого.
76.Доказать, что полное метрическое пространство может быть гомеоморфно неполному метрическому пространству.
77.Указать негомеоморфные топологические пространства, каждое из которых взаимно-однозначно и непрерывно отображается на другое.
78.Доказать, что проектирование топологического произведения X × Y
на любой сомножитель является непрерывным открытым (не обязательно замкнутым) отображением.
79.Является ли образ несвязного пространства при непрерывном отображении несвязным пространством?
80.Доказать, что взаимно-однозначное непрерывное отображение f
компактного пространства X на хаусдорфово пространство Y является гомеоморфизмом. Можно ли отказаться от требования хаусдорфовости пространства Y ?
81.Пусть X — топологическое пространство, а Y — компактное пространство. Доказать, что отображение pr : X × Y → X замкнуто.
82.Доказать, что всякая непрерывная функция на топологическом произведении любого семейства компактных хаусдорфовых пространств зависит от счетного числа координат.
83.Доказать, что метризуемое пространство X компактно тогда и только тогда, когда всякая метрика на X, согласованная с его топологией, ограничена.
84.Доказать, что метрическое пространство, являющееся непрерывным образом компакта, само является компактом.
85.Доказать, что непрерывное отображение одного компакта на другой
Дифференциальная геометрия и топология |
15 |
равномерно непрерывно.
86.Доказать, что непрерывная функция на компакте равномерно непре-
рывна.
16 |
О.В. Знаменская, В.В. Работин |
4.Параметрические уравнения кривых
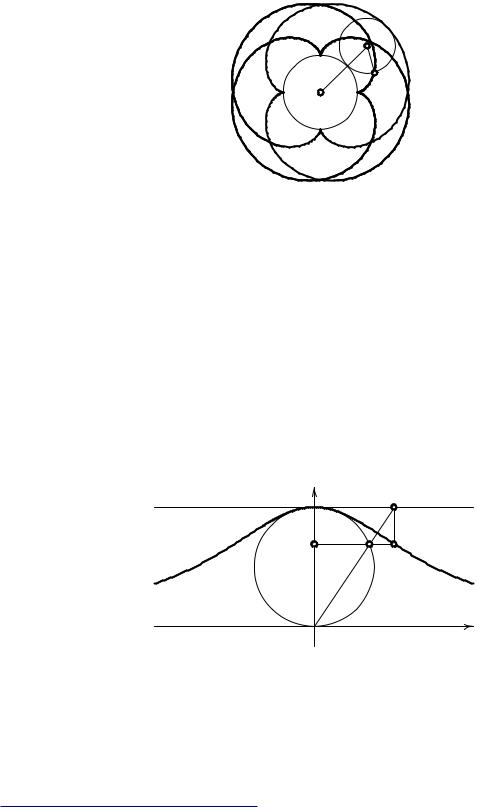
87.Окружность радиуса r катится без скольжения по окружности радиуса R, оставаясь вне ее.
r |
R M
Рис. II.30 Эпициклоида
Составьте уравнение траектории точки P , жестко связанной с подвижной окружностью и находящейся на расстоянии d от ее центра (эпициклоида, укороченная эпициклоида, удлиненная эпициклоида для случаев d = r, d < r, d > r, соответственно).
88. Произвольный луч OE пересекает в точках D и E окружность x2 + (y − a/2)2 = a2/4
и касательную к ней, проходящую через точку C, диаметрально противоположную O.
y |
M |
x |
O |
Рис. II.21 Локон Аньези
Через точки D и E проведены прямые, параллельные соответственно осям
OX и OY , до пересечения в точке M. Составьте уравнение кривой, образованной точками M (локон Аньези1).
89. Тракторист на тракторе торопится в трактир, расположенный на
1Мария Гаэтана Аньези (16.5.1718 – 4.8.1799) — зав. кафедрой математики в Болонье с 1750
г.
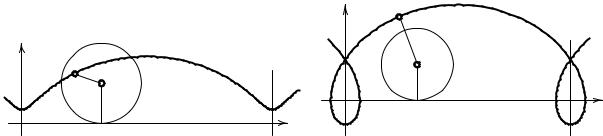
Дифференциальная геометрия и топология |
17 |
совершенно прямолинейном Московском тракте. Трактор тросом длины a
тянет за собой груз, который в начальный момент находился в поле на расстоянии a от тракта. Вывести уравнение траектории движения груза по полю. (Совсем не удивительно, что имя этой кривой — трактриса). Одна из простейших математических моделей описанной ситуации выглядит следующим образом: Найдите уравнение кривой C с постоянной длиной касательной GT = a (G — точка на кривой, T — точка пересечения касательной с осью OX, изображающей Московский тракт).
90. Прямая OL вращается вокруг точки с постоянной угловой скоростью ω, Точка M движется по прямой OL со скоростью, пропорциональной расстоянию |OM|. Составьте уравнение траектории, описываемой точкой
M(логарифмическая спираль).
91.Найдите кривую, задаваемую уравнением r = r(t), −∞ < t < ∞, если r′′(t) = a — постоянный ненулевой вектор.
92.Круг радиуса a катится по прямой без скольжения. Составьте уравнение траектории точки M, жестко связанной с кругом и находящейся на расстоянии d от его центра (при d = a циклоида, при d < a — укороченная циклоида, при d > a — удлиненная циклоида).
y M
y |
d |
|
d |
a |
x |
M |
|
||
|
a |
||
|
|
||
|
|
x |
|
O
Рис. II.31 Укороченная циклоида |
Рис. II.32 Удлиненная циклоида |
93.В пространстве две точки движутся так, что расстояние между ними остается постоянным. Докажите, что проекции их скоростей на направление прямой, соединяющей эти точки, равны между собой.
94.Точка M равномерно движется по прямой ON, равномерно вращающейся вокруг точки O. Составьте уравнение траектории точки M (спираль
18 |
О.В. Знаменская, В.В. Работин |
Архимеда2).
95. Найдите функцию r = r(ϕ), зная, что это уравнение в полярных координатах на плоскости определяет прямую линию.
y
M a
x
O
Рис. II.35 Циклоида
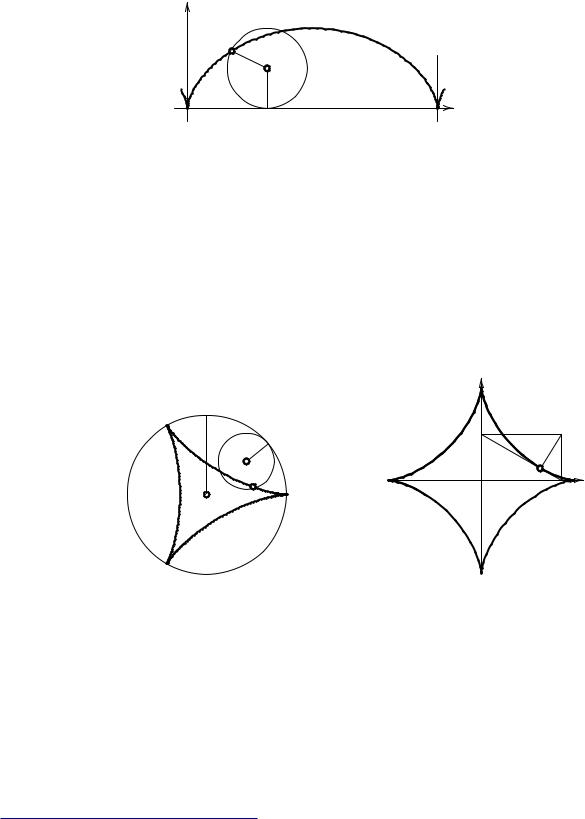
96. Окружность радиуса r катится без скольжения по окружности радиуса R, оставаясь внутри нее. Составьте уравнение траектории точки, жестко связанной с подвижной окружностью и находящейся на расстоянии d от ее центра (гипоциклоида, укороченная гипоциклоида, удлиненная гипоциклоида для случаев d = r, d < r, d > r, соответственно).
y
R |
r |
M |
|
M |
x |
|
|
O |
Рис. II.26 Кривая Штейнера |
Рис. II.29 Астроида |
97.Пусть C — некоторая плоская кривая, M0 — точка кривой C, xOy
—заданная в плоскости кривой прямоугольная система координат. Обозначим через T и N точки пересечения касательной и нормали к этой кривой с осью Ox и пусть P — проекция точки M0 на ось Ox.
а) Найдите уравнение кривой C, если ее поднормаль P N постоянна и равна a.
2Архимед (ок. 287 – 212 до н. э.) — древнегреческий математик, фмзик и механик.
Дифференциальная геометрия и топология |
19 |
б) Найдите уравнение кривой C, если ее подкасательная P T постоянна и равна a.
в) Найдите уравнение кривой C, если она имеет постоянную длину нормали M0N = a (для любой точки M0 на кривой).

20 |
О.В. Знаменская, В.В. Работин |
5. Кривизна кривой
Кривизной кривой r = r(s), где s — натуральный параметр, называется длина вектора кривизны (вектора ускорения) r′′(s), т.е. k = |r′′(s)|.
98.Запишите уравнение окружности радиуса R через натуральный параметр. Вычислите кривизну окружности радиуса R.
99.Точка M движется вдоль образующей прямого кругового цилиндра
суравнением x2+y2 = a2 с постоянной (относительно цилиндра) скоростью
b; при этом цилиндр вращается вокруг своей оси с постоянной единичной угловой скоростью.
а) Запишите параметрическое уравнение траектории точки M (винтовая линия);
б) Перейдите к натуральной параметризации винтовой линии; в) Вычислите кривизну винтовой линии.
100. Докажите, что если кривая в R3 задана в произвольной гладкой параметризации r = r(t), то ее кривизна вычисляется по формуле
|r′ × r′′| k = |r′|3 ,
где × — знак векторного произведения трехмерных векторов.
101.Найдите кривизну кривой ˜r = (2t, ln t, t2).
102.Докажите, что если кривая в R2 задана в полярных координатах
r = r(ϕ), то ее кривизна вычисляется по формуле
k = |r2 + 2r′2 − rr′′|
(r2 + r′2)3/2
103.Найдите кривизну кардиоиды r = a(1 + cos ϕ). Каковы минимум и максимум кривизны? Изобразите кардиоиду и проверьте правдоподобность формулы для кривизны.
104.Центром кривизны кривой называется точка, лежащая на главной
нормали к кривой (на том ее луче, на который указывает вектор кривизны) и отстоящая от точки пересечения нормали с кривой на расстояние k1,
