
Все работы по ИД МАТАНУ FAIT1 / VEKTORNAJA
.docИндивидуальное задание по векторной алгебре
(номер задачи из каждого задания соответствует номеру варианта, например, для варианта № 4 берутся задачи 1.4, 2.4, 3.4, и. т.д.
Задание 1.
Задать векторы
![]() и
и
![]() .
Построить векторы
.
Построить векторы
-
3
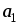 ,
,
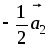 ,
,
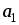 +2
+2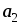 ,
,
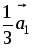 –
–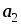
-
–2
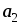 ,
3
,
3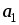 –
–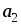 ,
,
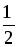
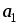 +
+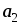
-
-3
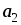 ,
2
,
2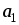 –
–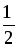
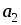 ,
,
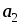 –
–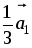
Дана треугольная пирамида АВСD. Построить (найти) векторы
-
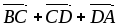 ,
,
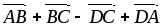
-
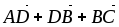 ,
,
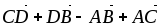
-
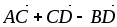 ,
,
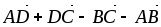
В параллелепипеде ABCDA1B1C1D1 построить
-
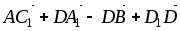 ,
,
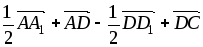
-
 ,
,
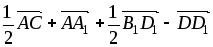
Построить равнодействующую сил, изображенных на рисунке
1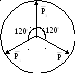
 .
9. 1.10.
.
9. 1.10.
Задание 2.
-
В параллелограмме ABCD рассмотрены
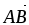 и
и
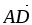 .
Доказать, что векторы
.
Доказать, что векторы
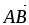 и
и
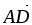 образуют
базис в R2 . Найти в
этом базисе координаты векторов
образуют
базис в R2 . Найти в
этом базисе координаты векторов
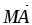 ,
,
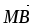 и 2
и 2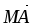 –
3
–
3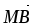 ,
где М – точка пересечения диагоналей.
,
где М – точка пересечения диагоналей. -
В параллелограмме ABCD обозначены
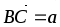 ,
,
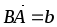 .
Доказать, что эти векторы образуют
базис в R2 . Найти в
этом базисе координаты векторов
.
Доказать, что эти векторы образуют
базис в R2 . Найти в
этом базисе координаты векторов
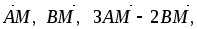 где М – точка пересечения диагоналей
параллелограмма.
где М – точка пересечения диагоналей
параллелограмма. -
В параллелограмме ABCD обозначены: О – точка пересечения диагоналей, Р – середина стороны ВС,
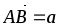 ,
,
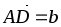 .
Доказать, что векторы
.
Доказать, что векторы
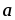 и
и
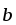 образуют базис в R2
. Найти в этом базисе координаты векторов
образуют базис в R2
. Найти в этом базисе координаты векторов
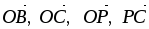 .
. -
В параллелограмме ABCD обозначены: О – точка пересечения диагоналей, Р – середина стороны ВС,
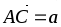 ,
,
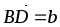 .
Доказать, что векторы
.
Доказать, что векторы
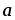 и
и
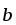 образуют базис в R2
. Найти в этом базисе координаты векторов
образуют базис в R2
. Найти в этом базисе координаты векторов
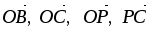 .
. -
В параллелепипеде ABCDA1B1C1D1 обозначены: М – середина ребра DD1,
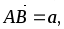
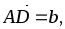
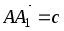 .
Доказать, что эти векторы образуют
базис в R3 . Найти в
этом базисе координаты векторов
.
Доказать, что эти векторы образуют
базис в R3 . Найти в
этом базисе координаты векторов
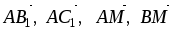 .
. -
В параллелепипеде ABCDA1B1C1D1 обозначены: М – середина ребра CC1, P – середина BC1,
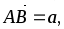
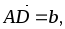
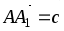 .
Доказать, что эти векторы образуют
базис в R3 . Найти в
этом базисе координаты векторов
.
Доказать, что эти векторы образуют
базис в R3 . Найти в
этом базисе координаты векторов
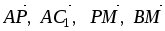 .
. -
В треугольной призме АВСА1В1С1 обозначены
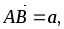
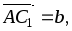
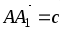 .
Доказать, что эти векторы образуют
базис в R3 . Найти в
этом базисе координаты векторов
.
Доказать, что эти векторы образуют
базис в R3 . Найти в
этом базисе координаты векторов
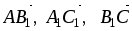 .
. -
В тетраэдре ABCD точки К и Р – соответственно середины ребер AC и BD,
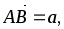
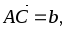
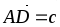 .
Доказать, что эти векторы образуют
базис в R3 . Найти в
этом базисе координаты векторов
.
Доказать, что эти векторы образуют
базис в R3 . Найти в
этом базисе координаты векторов
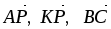 .
. -
В правильной четырехугольной пирамиде SABCD точка О – центр основания ABCD,
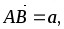
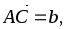
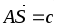 .
Доказать, что эти векторы образуют
базис в R3 . Найти в
этом базисе координаты векторов
.
Доказать, что эти векторы образуют
базис в R3 . Найти в
этом базисе координаты векторов
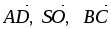 .
. -
В правильной четырехугольной пирамиде SABCD точка О – центр основания ABCD,
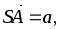
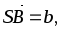
 .
Доказать, что эти векторы образуют
базис в R3 . Найти в
этом базисе координаты векторов
.
Доказать, что эти векторы образуют
базис в R3 . Найти в
этом базисе координаты векторов
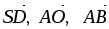 .
.
Задание 3.
Построить вектор
![]() с началом в точке А.
с началом в точке А.
|
|
Задание 4.
Даны точки А, В, С,
D. Найти координаты вектора
![]() .
.
-
А(-1,0 ,2 ), В( 1,2 ,1 ), С(3 , 7,-1 ), D(4 ,6 ,5 ),
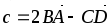
-
А(2,0,-1), В(-1,2,1), С(-1,3,7), D(5,6,4),
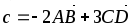
-
А(2,2,0), В(1,-2,1), С(3,-2,5), D(0,4,-2),
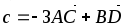
-
А(0,-1,2), В(3,1,0), С(-3,0,0), D(4,5,-6),
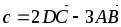
-
А(1,2,3), В(2,-1,0), С(3,0,3), D(7,-2,5),
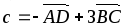
-
А(2,-3,1), В(0,2,2), С(-1,-1,0), D(0,6,0),
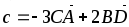
-
А(0,1,4), В(3,-2,7), С(2,5,-3), D(4,4,0),
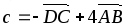
-
А(3,4,3), В(0,0,1), С(2,7,6), D(5,-1,-2),
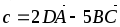
-
А(4,0,1), В(6,-2,5), С(-3,0,-3), D(7,1,2),
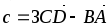
-
А(0,2,-3), В(1,-4,-6), С(7,2,2), D(0,5,0),
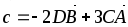
Задание 5.
Даны векторы
![]() и
и
![]() .
Найти : а) (
.
Найти : а) (![]() ,
,![]() );
б) орт вектора
);
б) орт вектора
![]() ;
в) направляющие косинусы вектора
;
в) направляющие косинусы вектора
![]() ;
г)
;
г)
![]() ;
д) проверить ортогональность, коллинеарность
векторов
;
д) проверить ортогональность, коллинеарность
векторов
![]() и
и
![]() .
.
-
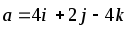 ,
,
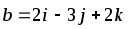
-
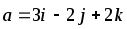 ,
,
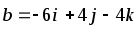
-
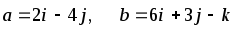 ,
, -
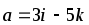 ,
,
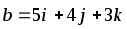
-
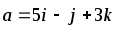 ,
,
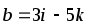
-
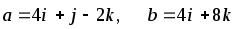
-
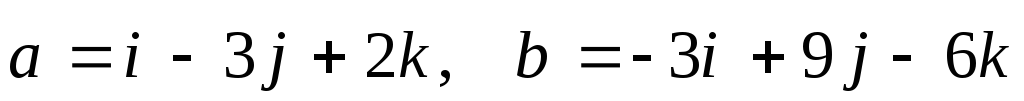
-
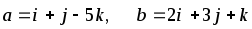
-
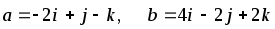
-
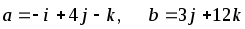
Задание 6.
Найти работу силы F при перемещении точки А в положение В.
-
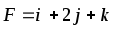 ,
А(-1,2,0), В(2,1,3)
,
А(-1,2,0), В(2,1,3) -
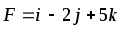 ,
А(1,2,-3), В(2,-1,3)
,
А(1,2,-3), В(2,-1,3) -
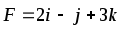 ,
А(3,-2,-1), В(4,-5,3)
,
А(3,-2,-1), В(4,-5,3) -
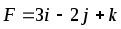 ,
А(1,-2,4), В(0,2,2)
,
А(1,-2,4), В(0,2,2) -
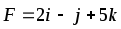 ,
А(3,2,1), В(1,2,3)
,
А(3,2,1), В(1,2,3) -
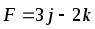 ,
А(1,3,-5), В(1,0,3),
,
А(1,3,-5), В(1,0,3),
-
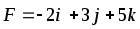 ,
А(-3,4,1), В – начало координат
,
А(-3,4,1), В – начало координат -
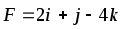 ,
А(1,2,-1), В – начало координат
,
А(1,2,-1), В – начало координат -
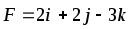 ,
А(3,2,1), В – начало координат
,
А(3,2,1), В – начало координат
-
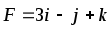 ,
А(-2,4,3), В(1,3,2)
,
А(-2,4,3), В(1,3,2)
Задание 7.
В начале координат приложены силы F1, F2, F3. Найти угол, который равнодействующая этих сил образует с указанной осью. Сделать чертеж.
-
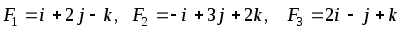 ,
ОХ
,
ОХ -
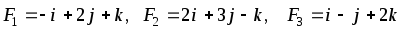 ,
ОУ
,
ОУ -
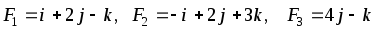 ,
OZ
,
OZ -
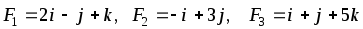 ,
OZ
,
OZ -
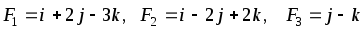 ,
ОУ
,
ОУ -
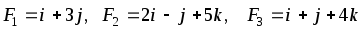 ,
ОУ
,
ОУ -
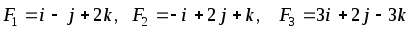 ,
ОХ
,
ОХ -
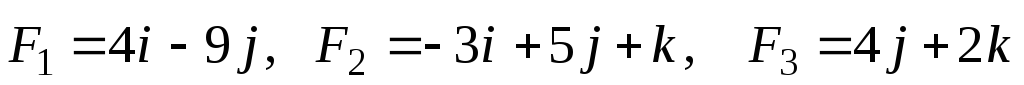 ,
ОХ
,
ОХ -
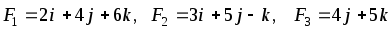 ,
ОХ
,
ОХ -
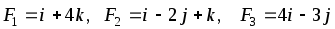 ,
OZ
,
OZ
Задание 8.
Найти площадь, периметр и углы треугольника АВС
-
А(1,-1,2), В(5,-6,2), С(1,3,-1)
-
А(2,-1,1), В(2,-6,5), С(-1,3,1)
-
А(3,5,-1), В(1,2,-1), С(-1,1,-3)
-
А(3,2,-1), В(1,2,5), С(2,-3,0)
-
А(0,-3,2), В(4,0,1), С(5,1,-1)
-
А(4,-1,0), В(2,3,4), С(6,-2,0)
-
А(1,2,2), В(-3,3,6), С(6,0,2)
-
А(7,0,1), В(2,-5,3), С(1,0,0)
-
А(1,2,4), В(3,-4,6), С(1,2,-5)
-
А(3,-2,4), В(3,2,-6), С(3,-1,1)
Задание 9.
Сила F приложена к точке А. Найти момент этой силы относительно точки В
|
|
Задание 10.
Используя свойства скалярного и векторного произведений векторов, упростить выражения (a,b,c произвольные векторы).
Задание 11.
Доказать, что точки А, В, С, D лежат в одной плоскости
-
А(1,2,-1), В(0,1,5), С(-1,2,1), D(2,1,3)
-
А(0,1,1), В(1,1,0), С(2,1,-1), D(2,3,1)
-
А(1,1,0), В(2,3,1), С(- 4,3,1), D(0,-1,-1)
Найти объем
параллелепипеда, построенного на
векторах
![]() ,
,
![]() ,
,
![]()
Установить,
образуют ли векторы
![]() ,
,
![]() ,
,
![]() базис в R3
базис в R3
Дополнительные задачи:
Номера дополнительных задач к вариантам:
|
|
-
На оси абсцисс найти точку М, расстояние от которой до точки А(3,-3) равно 5.
-
Три силы F, P, S приложены к одной точке и имеют взаимно перпендикулярные направления. Найти величину их равнодействующей , если |F| = 2, |P| = 10, |S| = 11.
-
Векторы
 ,
,
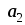 ,
,
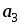 образуют правую тройку, взаимно
перпендикулярны, и |
образуют правую тройку, взаимно
перпендикулярны, и | |
= 4, |
|
= 4, |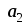 |
= 2, |
|
= 2, |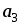 |
= 3. Вычислить
|
= 3. Вычислить
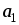 .
.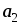 .
.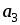 .
. -
Найти |c| , если с = 3
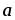 –
–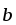 ,
если |
,
если |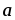 |=4,
|
|=4,
|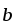 |=2,
(
|=2,
(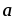
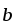 )
=
)
=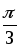 .
. -
Вычислить |[
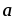 +
+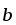 ,2
,2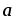 –
–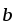 ]|,
если |
]|,
если |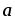 |=2,
|
|=2,
|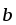 |=3,
(
|=3,
(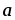
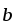 )
=
)
=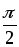 .
. -
Доказать, что для любых векторов
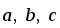 векторы
векторы
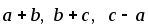 компланарны.
компланарны. -
Доказать тождество
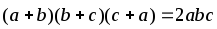
-
Векторы
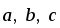 –
не компланарные. Доказать, что векторы
–
не компланарные. Доказать, что векторы
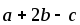 ,
,
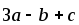 ,
,
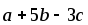 компланарны.
компланарны. -
Найти вектор х, образующий со всеми базисными ортами равные острые углы, если |х | =
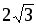 .
. -
Найти координаты вектора х, если известно, что он перпендикулярен векторам
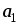 =(4,-2,-3),
=(4,-2,-3),
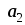 =(0,1,3)
, образует с ортом j
тупой угол и |х
| =26.
=(0,1,3)
, образует с ортом j
тупой угол и |х
| =26. -
Вычислить площадь параллелограмма, диагоналями которого служат векторы 2
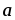 –
–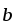 и 4
и 4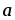 –5
–5 ,
где
,
где
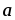 и
и
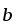 –
единичные векторы, (
–
единичные векторы, (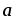
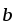 )
=
)
=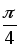 .
. -
Вне плоскости параллелограмма АВСD взята точка О. В базисе
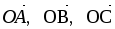 найти координаты вектора
найти координаты вектора
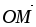 ,
где М – точка пересечения диагоналей
параллелограмма.
,
где М – точка пересечения диагоналей
параллелограмма. -
А(-2,6) и В(2,8) – две смежные вершины параллелограмма, Р(2,2) – точка пересечения его диагоналей. Найти две другие вершины.
-
AD, BE, CK – медианы треугольника АВС. Доказать AD + BE + CK = 0.
-
Найти длину высоты тетраэдра ABCD , опущенной из вершины D , если А(2,3,1), В(4,1,-2), С(6,3,7), D(-5,-4,8).
-
Даны векторы
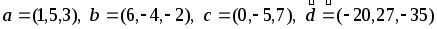 .
Подобрать числа ,
,
так, чтобы векторы
.
Подобрать числа ,
,
так, чтобы векторы
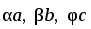 и
и
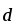 образовывали замкнутую ломаную.
образовывали замкнутую ломаную. -
Три ненулевых вектора
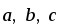 связаны
соотношением
связаны
соотношением
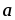 =[
=[ ,
,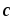 ],
],
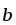 =[
=[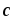 ,
,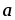 ]
,
]
,
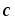 =[
=[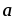 ,
,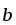 ].
Найти длины этих векторов и углы между
ними.
].
Найти длины этих векторов и углы между
ними. -
Даны векторы
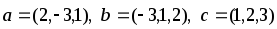 .
Проверить , верно ли равенство
.
Проверить , верно ли равенство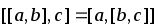 .
.
