
Все работы по ИД МАТАНУ FAIT1 / KOMPLEKSNIE
.docИндивидуальное задание «Комплексные числа и многочлены».
Номер варианта указывает преподаватель. Номера задач из каждого задания, соответствующие варианту, указаны в таблице:
|
Задание вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
N (N =1,2,3,…,10) |
1.N |
2.N |
3.N |
4.N |
5.N |
6.N |
7.N |
|
например, для варианта № 4 – задачи 1.4, 2.4, 3.4, 4.4, 5.4, 6.4, 7.4 |
|||||||
|
11 |
1.1 |
2.2 |
3.3 |
4.4 |
5.5 |
6.6 |
7.7 |
|
12 |
1.2 |
2.3 |
3.4 |
4.5 |
5.6 |
6.7 |
7.1 |
|
13 |
1.3. |
2.4 |
3.5 |
4.6 |
5.7 |
6.8 |
7.9 |
|
14 |
1.4. |
2.5. |
3.6. |
4.7 |
5.8 |
6.9 |
7.10 |
|
15 |
1.5 |
2.6 |
3.7 |
4.8 |
5.9 |
6.10 |
7.1 |
|
16 |
1.6 |
2.7 |
3.8 |
4.9 |
5.10 |
6.7 |
7.8 |
|
17 |
1.7 |
2.8 |
3.9 |
4.10 |
5.6 |
6.8 |
7.9 |
|
18 |
1.8 |
2.9 |
3.10 |
4.5 |
5.7 |
6.9 |
7.10 |
|
19 |
1.9 |
2.10 |
3.4 |
4.6 |
5.8 |
6.10 |
7.1 |
|
20 |
1.10 |
2.2 |
3.5 |
4.7 |
5.9 |
6.1 |
7.2 |
|
21 |
1.2 |
2.3 |
3.6 |
4.8 |
5.10 |
6.2 |
7.3 |
|
22 |
1.3 |
2.4 |
3.7 |
4.9 |
5.1 |
6.3 |
7.4 |
|
23 |
1.4 |
2.5 |
3.8 |
4.10 |
5.2 |
6.4 |
7.5 |
|
24 |
1.5 |
2.6 |
3.9 |
4.1 |
5.3 |
6.5 |
7.6 |
|
25 |
1.6 |
2.7 |
3.10 |
4.2 |
5.4 |
6.6 |
7.7 |
|
26 |
1.7 |
2.8 |
3.1 |
4.3 |
5.5 |
6.7 |
7.8 |
|
27 |
1.8 |
2.9 |
3.2 |
4.4 |
5.6 |
6.8 |
7.9 |
|
28 |
1.9 |
2.10 |
3.3 |
4.5 |
5.7 |
6.9 |
7.10 |
|
29 |
1.10 |
2.3 |
3.4 |
4.6 |
5.8 |
6.10 |
7.1 |
|
30 |
1.4 |
2.4 |
3.5 |
4.7 |
5.9 |
6.1 |
7.2 |
|
31 |
1.5 |
2.5 |
3.6 |
4.8 |
5.10 |
6.2 |
7.3 |
|
32 |
1.6 |
2.6 |
3.7 |
4.9 |
5.1 |
6.3 |
7.4 |
|
33 |
1.7 |
2.7 |
3.8 |
4. 10 |
5.2 |
6.4 |
7.5 |
|
34 |
1.8 |
2.8 |
3.9 |
4.1 |
5.3 |
6.5 |
7.6 |
|
35 |
1.9 |
2.9 |
3.10 |
4.2 |
5.4 |
6.6 |
7.7 |
|
36 |
1.10 |
2.10 |
3.1 |
4.3 |
5.5 |
6.7 |
7.8 |
|
36 |
1.5 |
2.4 |
3.2 |
4.4 |
5.6 |
6.8 |
7.9 |
|
38 |
1.6 |
2.5 |
3.3 |
4.5 |
5.7 |
6.9 |
7.10 |
|
39 |
1.7 |
2.6 |
3.4 |
4.6 |
5.8 |
6.10 |
7.1 |
|
40 |
1.8 |
2.7 |
3.5 |
4.7 |
5.9 |
6.1 |
7.2 |
Задание 1. Изобразить на комплексной плоскости заданные числа. Выполнить графически операции: z1 + 2z2, 3z3 – z4 , –2z5 +z2.
-
z1 = 2i, z2 = 3 + i, z3 = –1, z4 =3(cos
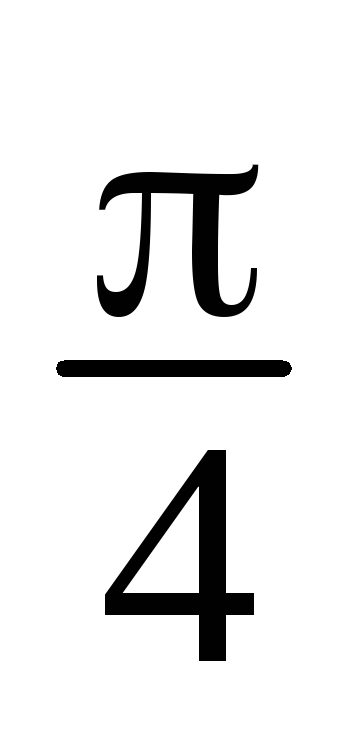 +isin
+isin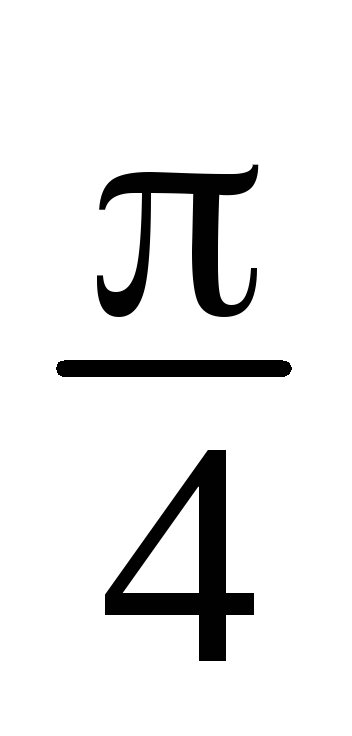 ), z5
= –1 +2i.
), z5
= –1 +2i. -
z1 = -3i, z2 = 4 – i, z3 =
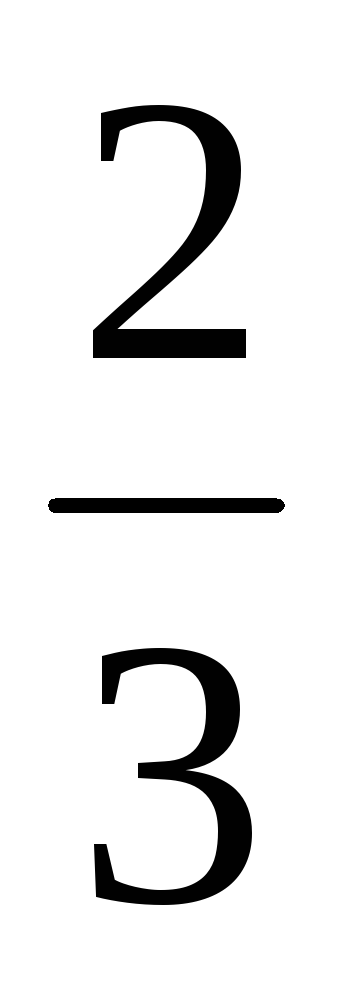 +
i,
z4
=2(cos
+
i,
z4
=2(cos
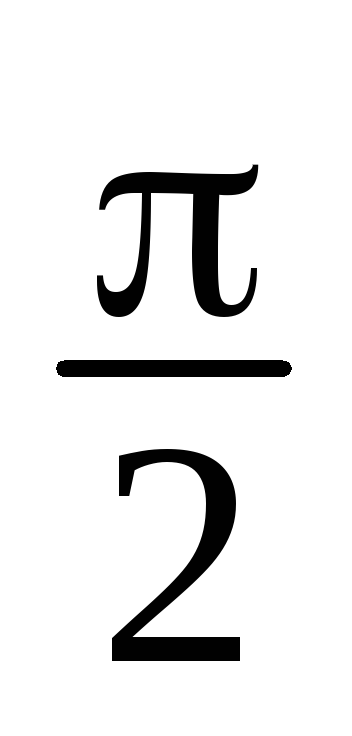 +isin
+isin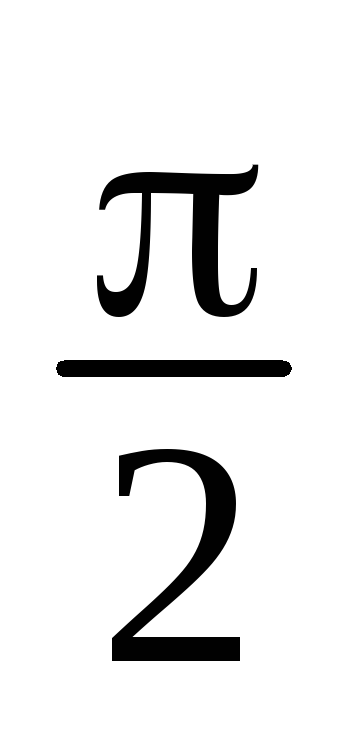 ), z
5
= 2
), z
5
= 2
-
z1 = -1+2i, z2 = -3i, z3 = 4 -3i, z4 = 3(cos +isin ), z 5 = -2,5
-
z1 = -4i, z2 = 5+2i, z3 =
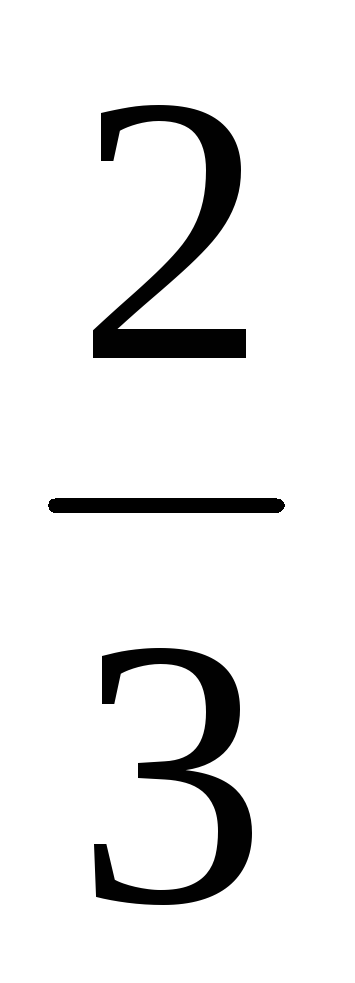 i,
z4
= 4(cos
i,
z4
= 4(cos
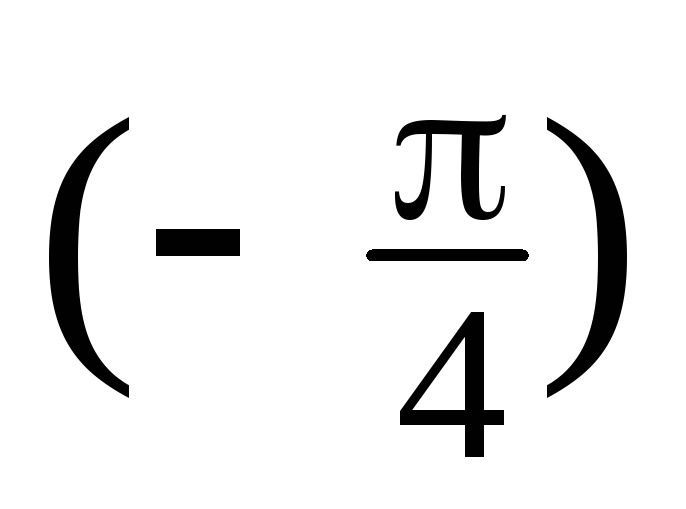 +isin
+isin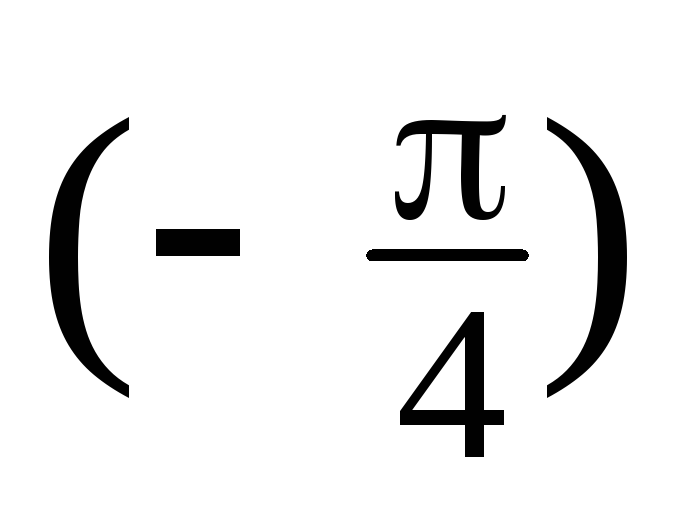 ), z
5
= -2
), z
5
= -2 -
z1 = 3-2i, z2 = -3i, z3 = -1 + i, z4 = 2(cos
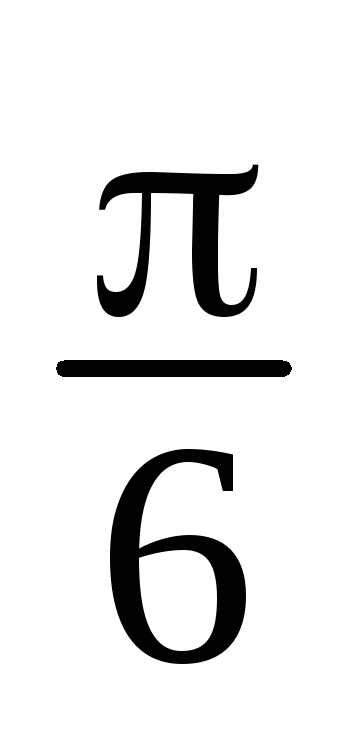 +isin
+isin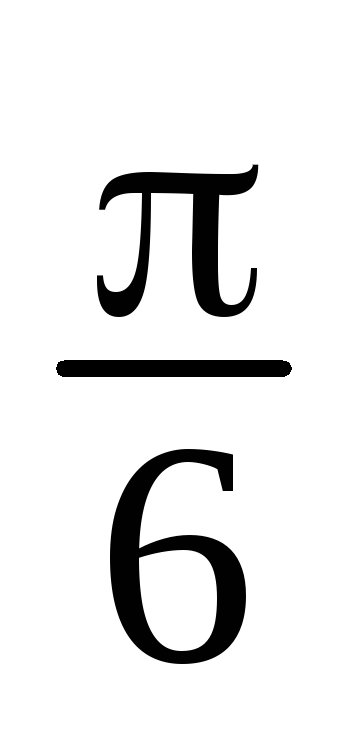 ),
z
5
= -1
),
z
5
= -1 -
z1 = 4+2i, z2 = 2–3i, z3 = 4i, z4 = 1(cos
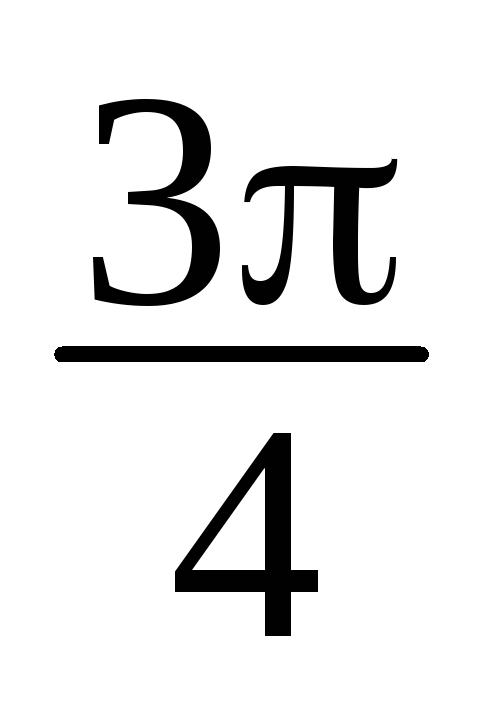 +isin
+isin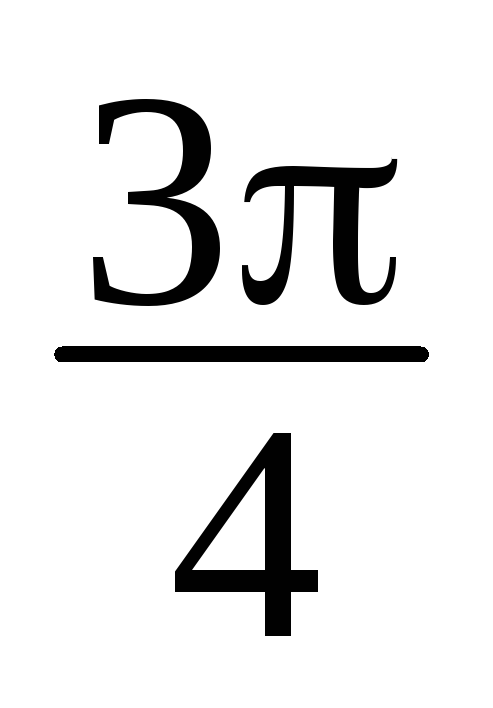 ), z
5
= -3
), z
5
= -3 -
z1 = 5– i, z2 = -3+2i, z3 = - i, z4 = 2(cos
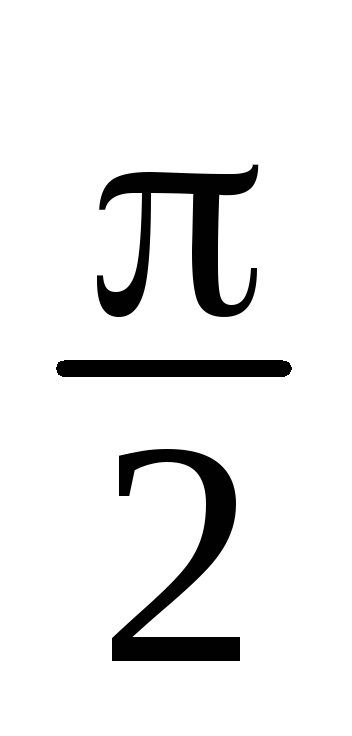 +isin
+isin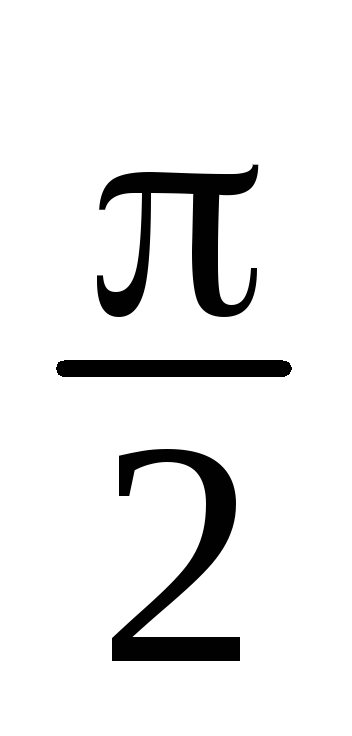 ), z
5
= 3
), z
5
= 3 -
z1 = 4+ i, z2 =2– 3i, z3 = -4i, z4 = 3(cos2+isin2 ), z 5 = 1,5
-
z1 = 3+2i, z2 = -3i, z3 =2– i, z4 = 2(cos
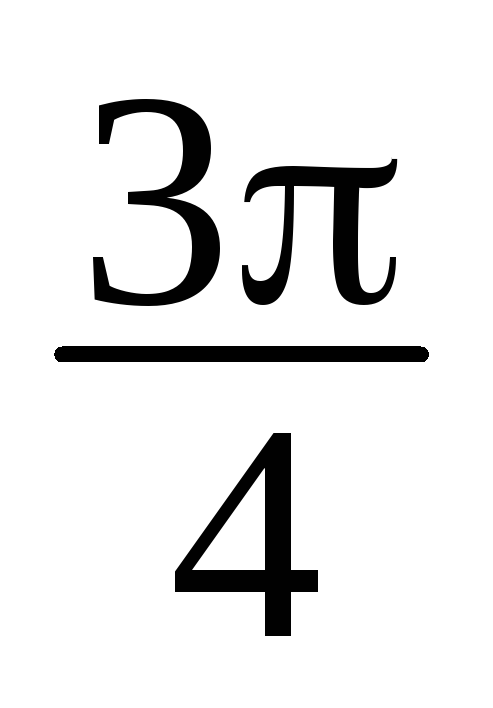 +isin
+isin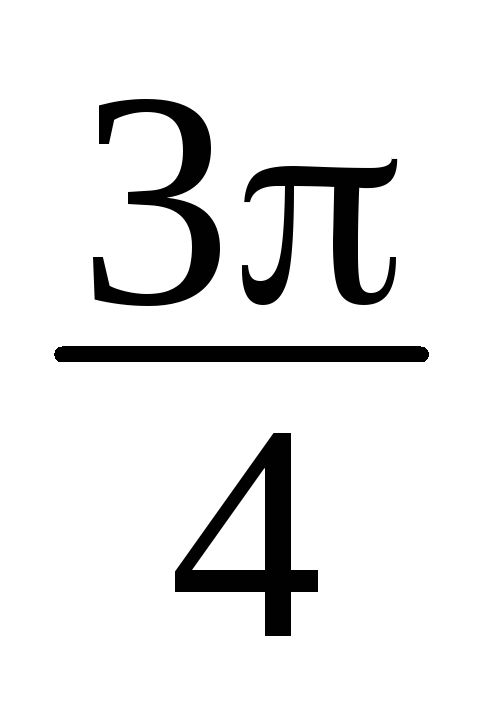 ), z
5
= 4
), z
5
= 4 -
z1 = 2i, z2 = -1+ i, z3 = -
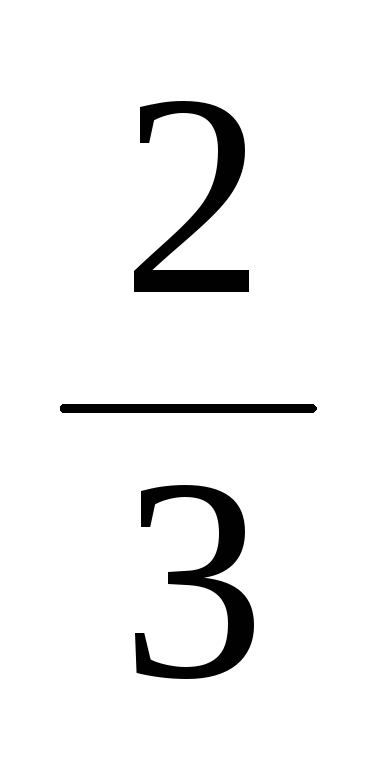 i,
z4
=3(cos
i,
z4
=3(cos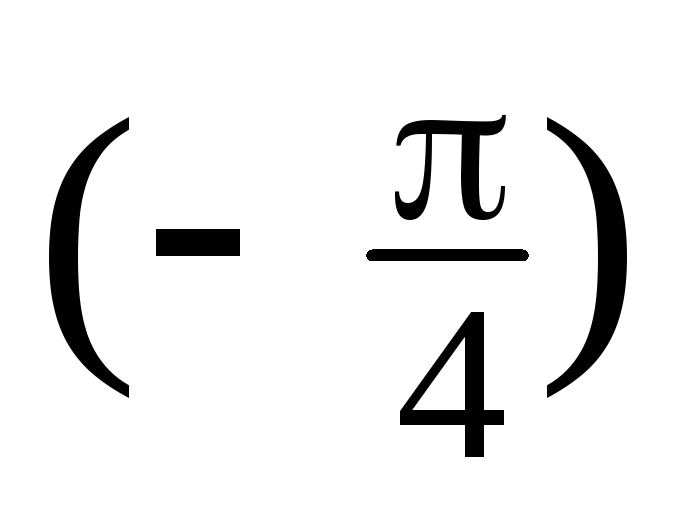 +isin
+isin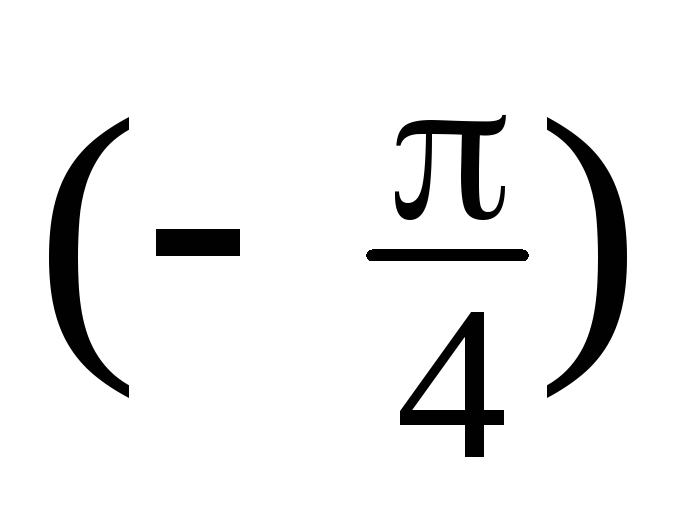 ), z
5
= -2,5
), z
5
= -2,5
Задание 2. Найти значение выражения. Результат записать в трех формах. Изобразить результат на комплексной плоскости
2.1. а)
![]() б)
б)
![]()
в) Найти f(1+i)
, если
![]()
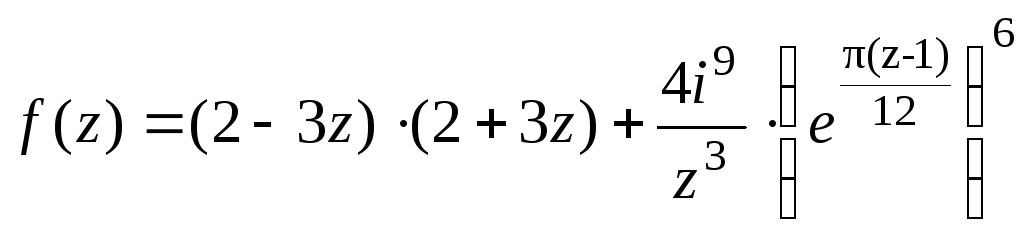
2.2. а)
![]() б)
б)
![]()
в) Найти f (2i)
, если
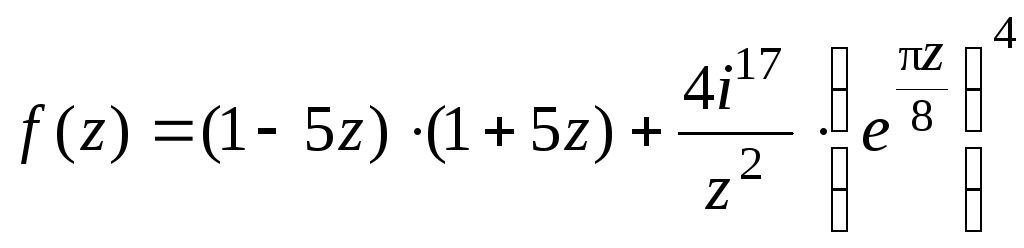
2.3. а)
![]()
в)
Найти f
(i),
если
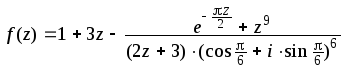
2.4.
а)
![]()
в) Найти f (-2i),
если
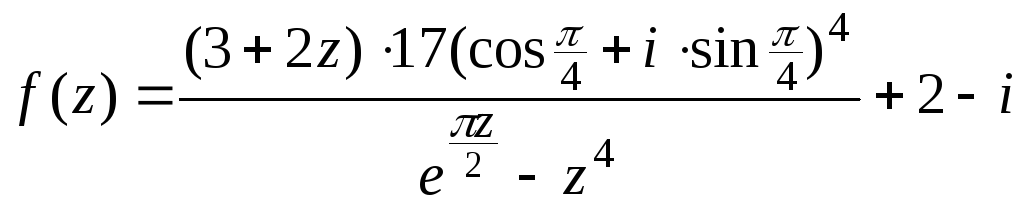
2.5. а)![]()
в)
Найти f
(i),если
f(z)
=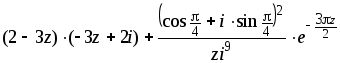
2.6.
а)
![]()
в)
Найти f
(2i),
если
![]()
2.7.
а)
![]()
в)
Найти f
(2i),
если
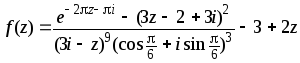
2.8.
а)![]()
в)
Найти f
(i-1),
если
![]()
-
а)
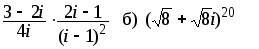
в) Найти f (3i),
если
![]()
-
а)
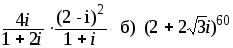
в) Найти f (-2i),
если
![]() .
.
Задание 3. Найти корни уравнения и изобразить их на комплексной плоскости:
3.1. а) z 5 + i – 1 = 0 б) z2 + z = 0 3.2. а) z3 +i – 1 = 0 б) z2 + |z| = 0
3.3. а) z4 +2-2i = 0 б) z2 = (|z| – 6)i 3.4. а) z4-1-i = 0 б) z2 + |z | = 4iJmz
3.5. а) z5 -1-i = 0 б) z|z | = 3 – 4i 3.6. а) z5-32-32i = 0 б) z|z | +2z + i = 0
3.7. а) z6 +6i = 0 б)2|z | + (2 – 4i)z = 1 – 5i 3.8. а) z4+16 =0 б) z2 – 3z = 0
3.9. а) z3+2+2i = 0 б) z2 + |z| = 2iJmz 3.10.а) z4 +1-i = 0 б) z|z | +4z + 3i = 0
Задание 4. Изобразить на комплексной плоскости область, заданную условиями
4.1.
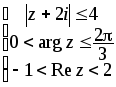 4.2.
4.2.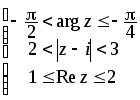 4.3.
4.3.
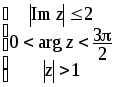
4.4.
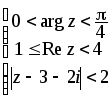 4.5.
4.5.
 4.6.
4.6.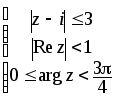 4.7.
4.7.
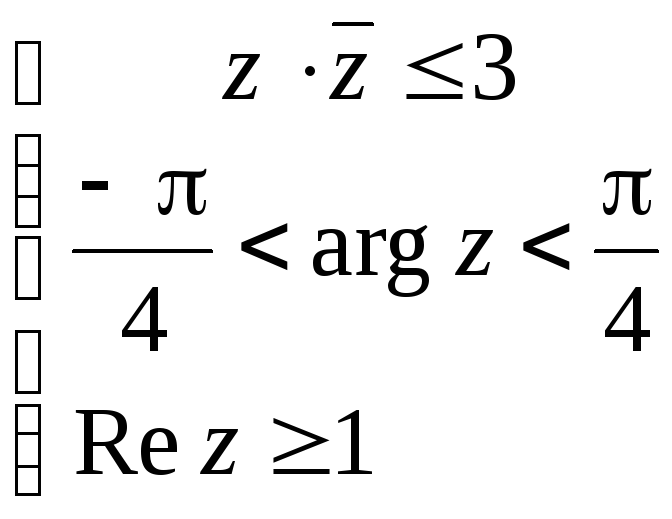
4.8.
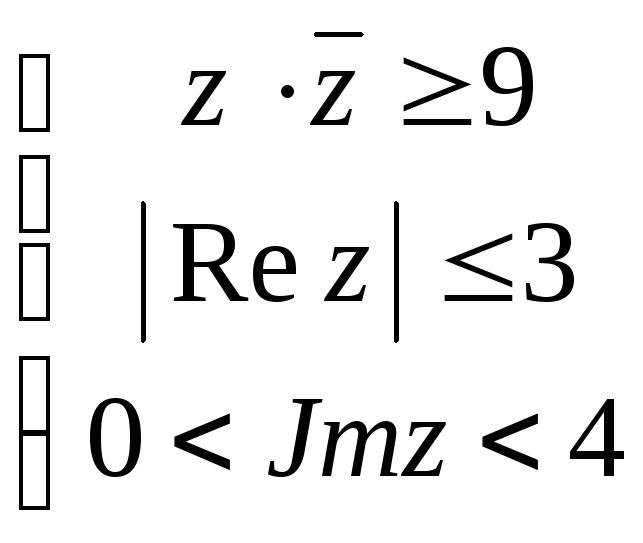 4.9.
4.9.
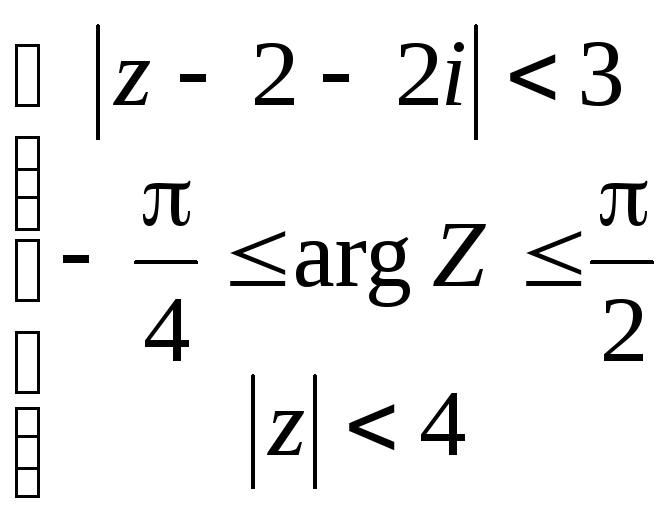 4.10.
4.10.
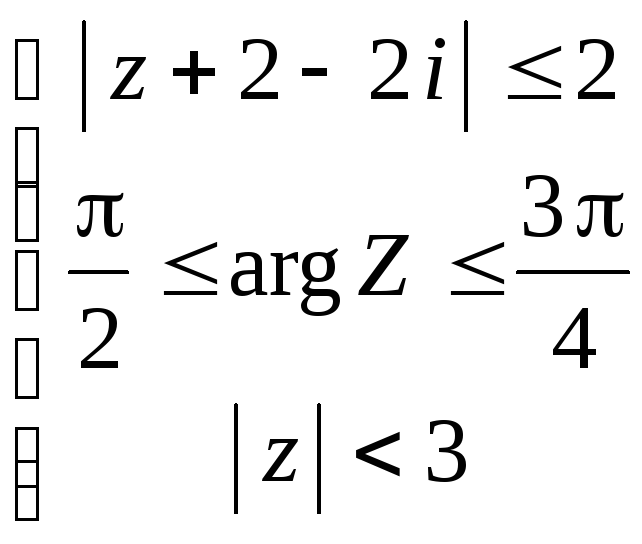
Задание 5. Выполнить деление одного из многочленов на другой:
-
а) 2x5 + 6x +7 на x3 -2x +1; б) х6 на 1– х
-
3x7 – 2 на x2 –3x; б) х5 на 2 – х
-
2x5 – 4x на x3 – 4; б) х6 на х +2
-
7x6 -4x2 +5 на -7x3 +3x; б) х5 на х+1
-
2x5 -4x+ 6 на x2 –4; б) х6 на 2+х
-
7x7 + 2x2 -4 на 7x3 +4 ; б) х5 на х– 1
-
5x6 + x4 - x на 5x5 – 2; б) х5 на 2 – х
-
x8 +4x2-2 на x5 -4x+1; б) 4х5 на 1– х
-
x6+3x2 - 4x на x3 - 2x + 1; б) 3х5 на 2–х
-
x4 +2x3 + 3x на 2x2 – 4; б) 5х6 на 1– х
Задание 6. Разложить заданный многочлен на неприводимые множители:
-
x5 + x4 - 7x3 - 11x2 - 8x - 12
-
x5 - 2x4 - 5x3 - 8x2 - 14x -8
-
x5 +4 x4 - x3 - 10x2 - 6x -36
-
x5 - 3x4 + 5x3 -11x2 +20
-
x5 +x4 -4x3 -8x2 -32x -48
-
x5 +5x4 + 4x3 – 4x2 +3x – 9
-
x5 - x4 - 7x3 +11x2 -8x +12
-
x5 -3x4 + 2x3 - 2x2 +8
-
x5 - 2x4 - 6x3 - 6x2 - 7x - 4
-
x5 - x4 - 3x3 - 5x2 - 10x -6
Задание 7. Разложить дробь на сумму простейших:
7.1.![]() 7.2.
7.2.
![]()
7.3. a)![]() 7.4.a)
7.4.a)
![]()
7.5. a)![]() 7.6. a)
7.6. a)![]()
7.7. a)
![]() .
7.8. a)
.
7.8. a)
![]()
-
a)
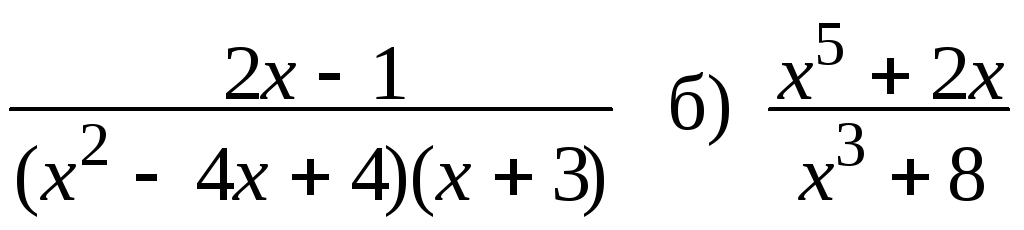 7.10. a)
7.10. a)

Вопросы для защиты темы:
Комплексные числа и многочлены.
1 уровень.
-
Дайте определение комплексного числа, его действительной, мнимой части. Как обозначают действительную и мнимую часть комплексного числа? Какую форму записи комплексного числа называют алгебраической?
-
Как геометрически можно изобразить комплексное число? Приведите пример. Какую плоскость называют комплексной плоскостью?
-
Какие числа называют комплексно-сопряженными, противоположными? Приведите примеры. Как геометрически изображаются эти числа?
-
Когда комплексные числа называются равными? Что означает каждое из утверждений: а) число
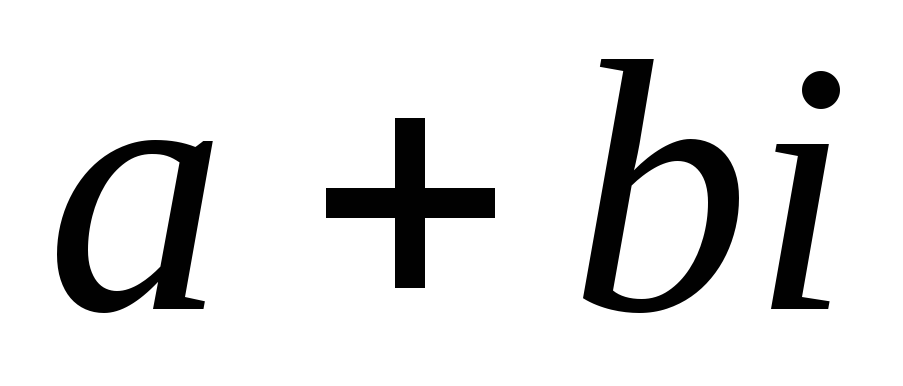 равно нулю; б) число
равно нулю; б) число
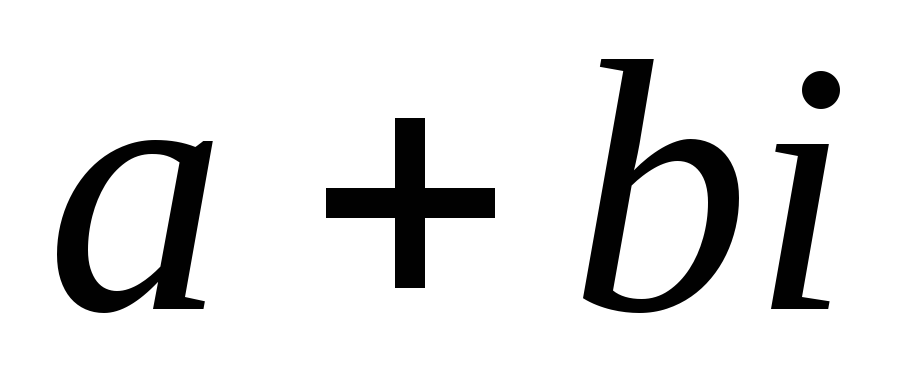 не равно нулю; в) числа
не равно нулю; в) числа
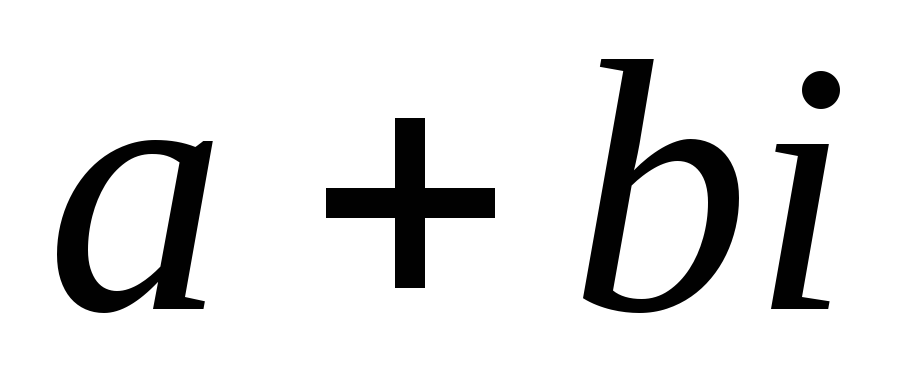 и
и
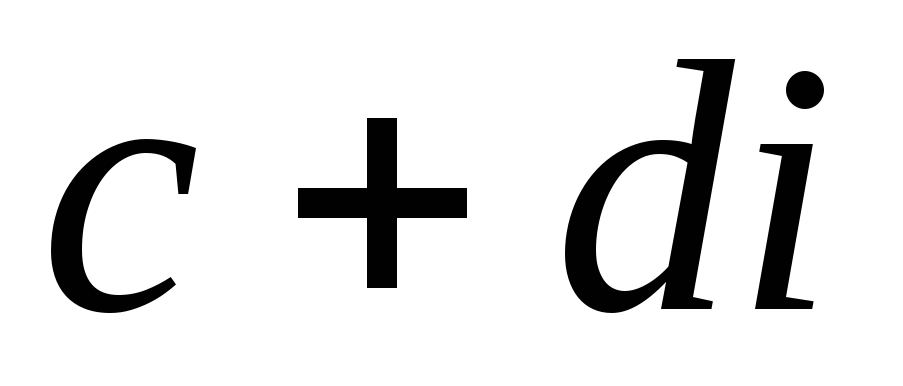 различны?
различны? -
Как выполняются операции сложения, вычитания, умножения, деления комплексных чисел в алгебраической форме? Приведите пример.
-
Дайте определение модуля и аргумента комплексного числа z = x + yi. Как они обозначаются? Как найти модуль и аргумент? Приведите пример.
-
Как связаны между собой модули и аргументы комплексно сопряженных чисел, противоположных чисел?
-
Какие формы записи комплексного числа вы знаете? Как осуществляется переход от одной формы к другой? Приведите пример.
-
Какие из операций над комплексными числами удобнее выполнять в алгебраической форме?
-
Как выполняются операции умножения и деления комплексных чисел, заданных в тригонометрической форме? Запишите формулу Муавра.
-
Какую операцию над комплексными числами можно выполнить только в тригонометрической или показательной форме? Определите эту операцию, приведите пример.
-
Какие операции над комплексными числами можно выполнить в любой форме записи? В каких случаях рациональнее воспользоваться той или иной формой записи? Приведите примеры.
-
Каков геометрический смысл выражения |z1 – z2|?
-
Опишите с помощью неравенства множество точек полуплоскости, расположенной справа от мнимой оси; ниже действительной оси.
-
Дайте определение многочлена (полинома) от одной неизвестной. Приведите пример многочлена 4-ой степени с действительными коэффициентами, пример многочлена нулевой степени.
-
Какие многочлены называются равными? Приведите пример.
-
Дайте определение суммы и произведения двух многочленов, произведения многочлена на число, приведите примеры.
-
Сформулируйте теорему о делении многочлена на многочлен с остатком, приведите пример. Дайте понятие неполного частного, остатка от деления многочленов.
-
Дайте определение корня многочлена. Сформулируйте необходимое и достаточное условие, при котором число a есть корень многочлена.
-
Дайте определение простого и кратного корня многочлена. Приведите пример многочлена второй степени, имеющего простые корни; кратный корень.
-
Может ли многочлен с действительными коэффициентами иметь комплексные корни? Если да, то какие это корни?
-
Что значит – разложить многочлен на множители? Приведите пример.
-
Запишите общий вид разложения многочлена степени п на линейные множители. Когда многочлен с действительными коэффициентами можно разложить на линейные множители с действительными коэффициентами?
-
Какой многочлен называется неприводимым (неразложимым) на множестве действительных чисел? Приведите примеры неприводимых многочленов с действительными коэффициентами.
-
При каком условии многочлен с действительными коэффициентами можно разложить на неприводимые множители первой и второй степени? Приведите пример.
-
Дайте понятие рациональной дроби. Какая рациональная дробь называется правильной, неправильной? Приведите примеры.
-
Как выделить целую часть неправильной рациональной дроби? Приведите пример.
-
Какие рациональные дроби называют простейшими (элементарными)?
-
Сформулируйте алгоритм разложения правильной рациональной дроби на сумму простейших.
2 уровень
-
Может ли сумма квадратов двух комплексных чисел быть отрицательной? Приведите пример.
-
Найдите все числа, сопряженные своему квадрату.
-
Дайте геометрическое описание множества всех точек удовлетворяющих условию:
а) | z |>1 – Re z; б) z =`z; в) | z – i | = | z + 2|; г) | z –2i | £ 3.
д) | p
–arg z | <
![]() ;
е) z =`z.
;
е) z =`z.
-
При каких условиях модуль суммы двух комплексных чисел равен разности модулей слагаемых?
-
При каких условиях модуль суммы двух комплексных чисел равен сумме модулей слагаемых?
-
При каком условии квадрат комплексного числа есть а) действительное число, б) чисто мнимое число?
-
Выяснить, при каких условиях произведение двух комплексных чисел есть чисто мнимое число.
-
Докажите, что | z1 + z2 |2 +| z1 – z2 |2 = 2 (| z1|2+| z2 |2). Каков геометрический смысл этого неравенства?
-
Докажите, что
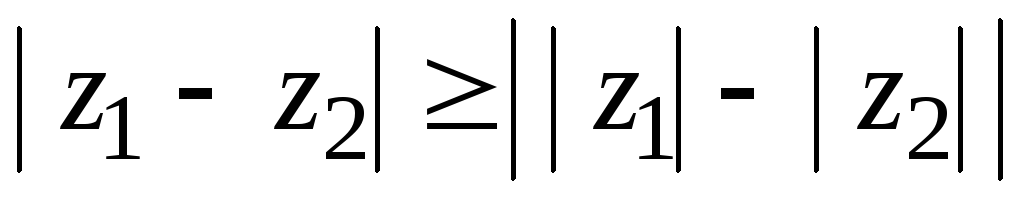 .
Каков геометрический смысл этого
неравенства?
.
Каков геометрический смысл этого
неравенства?
-
Докажите, что модуль произведения двух комплексных чисел равен произведению модулей этих чисел.
-
Используя формулу Муавра, выразите через cosj и sinj функцию cos4j.
-
Представьте в тригонометрической форме комплексные числа:
а) z = 1+ cos![]() + i.sin
+ i.sin![]() ;
б) z = –cos
;
б) z = –cos![]() + i.sin
+ i.sin
![]() ;
;
в) z = 1 + cos2a
+ isin2a ,
![]() <
a < p
г) z = 1 + itga,
0<a<
<
a < p
г) z = 1 + itga,
0<a<![]() .
.
-
Запишите в показательной форме числа:
а)
sina –i
cosa,
0<a<![]() б) sina
+i(1 –
cosa),
0<a<
б) sina
+i(1 –
cosa),
0<a<![]() .
.
-
Докажите формулы Эйлера
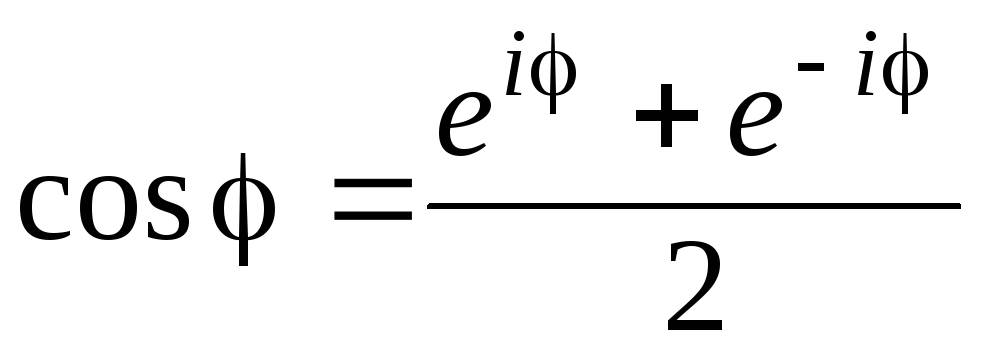 ,
,
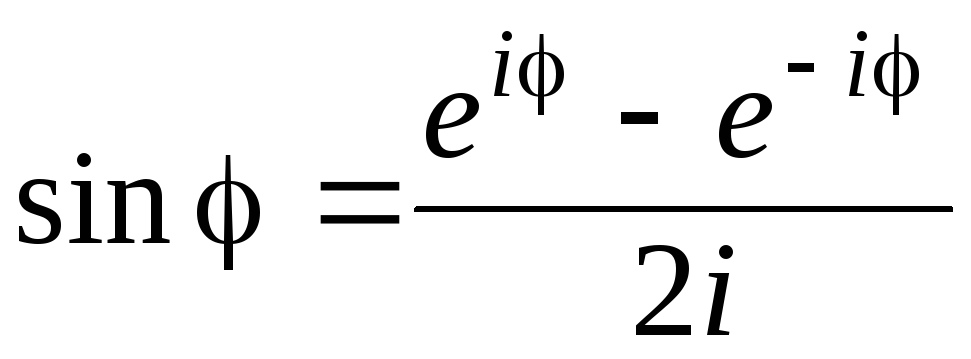 .
.
-
Докажите равенства:
а)
![]() ;
б)
;
б)
![]() ;
в) z +`z
= 2Re z; г) z –`z
= 2i Im z.
;
в) z +`z
= 2Re z; г) z –`z
= 2i Im z.
16) Точки А и В изображают на комплексной плоскости числа z1 = 6 + 8i и z2 = 4 – 3i соответственно. Найдите хотя бы одно такое число z, чтобы изображающая его точка С лежала на биссектрисе угла АОВ.
17) Вычислить
![]() ,
где п
– целое положительное число.
,
где п
– целое положительное число.
18) Чему равен
![]() ,
если
,
если
![]() ?
?
-
Может ли квадратное уравнение с действительными коэффициентами иметь корни 1 + i и 1-2i ?
-
Определить коэффициент а так, чтобы многочлен z5 – az2 – az + 1 имел число (-1) корнем кратности не ниже двух.
-
Многочлен z4 + 4z3 + 11z2 + 14z + 10 разложить на множители первой и второй степени с действительными коэффициентами, если известен один корень z1 = –1 + i.
-
При каких значения А и В многочлен Az4 + Bz3 + 1 делится на многочлен (z - 1)2 без остатка?
-
При каком значении а число z = 2i является корнем многочлена z3 – (a + 1)z2 + 4аz + 8(а2 – 2)?
-
Определите a так, чтобы один из корней уравнения z3 –7z + a = 0 равнялся удвоенному другому.
-
Определите a, b, c так, чтобы они были корнями уравнения z3– az2 + bz+ c = 0
-
Постройте многочлен наименьшей степени, корнями которого являются числа: -1 и 2 – простые корни, 1 + i – двукратный.
-
Найдите необходимые и достаточные условия приводимости многочлена z4 + pz2 + q с действительными коэффициентами.
-
Докажите, что всякий многочлен третьей степени приводим на множестве действительных чисел.
-
Докажите, что число 1 является корнем многочлена тогда и только тогда, когда сумма его коэффициентов равна 0.
-
При каком значении а Î R число
 является корнем многочлена z3
– (a+3)z2 + 6a2z
+ a2 – 5. Найдите остальные корни
этого многочлена при найденном значении
а.
является корнем многочлена z3
– (a+3)z2 + 6a2z
+ a2 – 5. Найдите остальные корни
этого многочлена при найденном значении
а. -
Решите уравнение z8 +6z4 +9 = 0.
-
Пользуясь схемой Горнера, вычислить Р(x0), если х0 =–2–i, P(x) = x5 +(1+2i)x4 – (1+3i)x2 +7.
