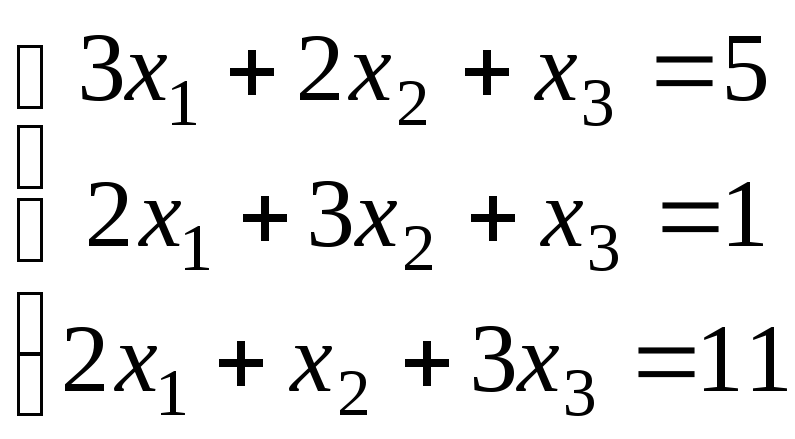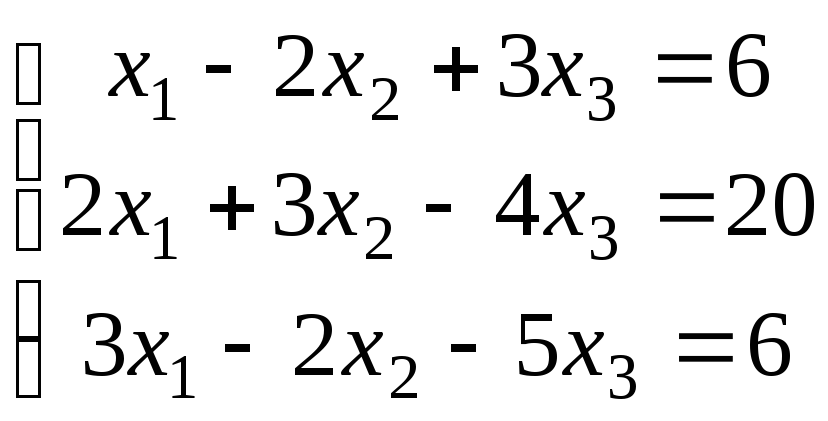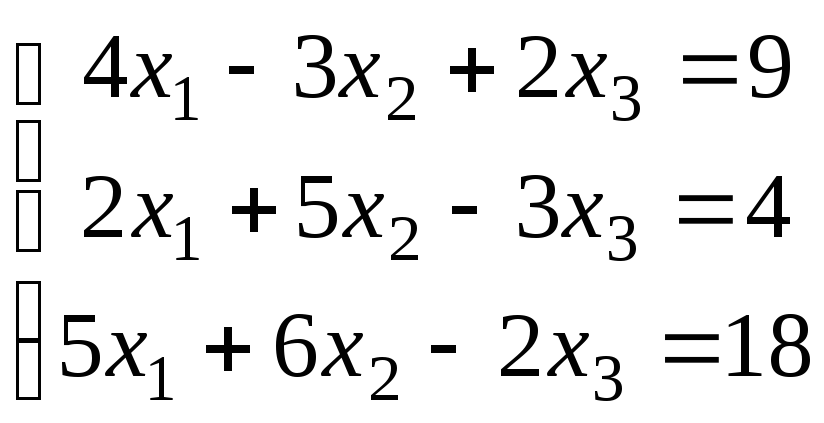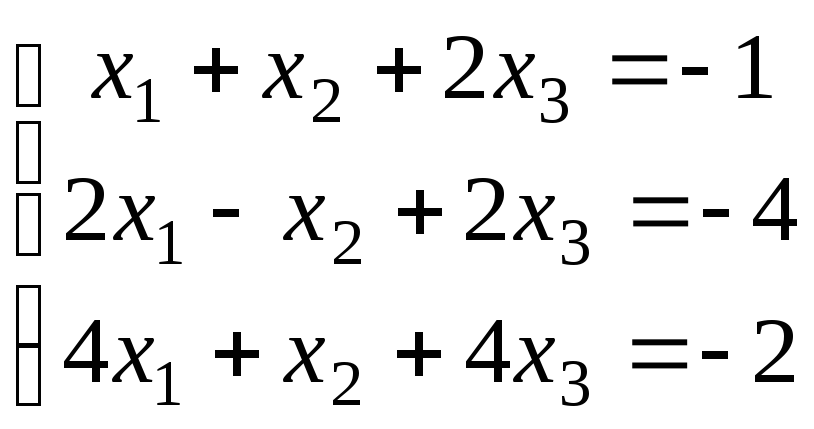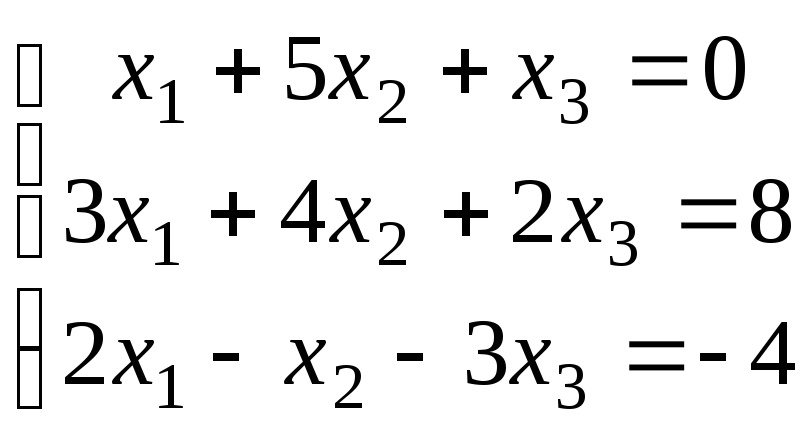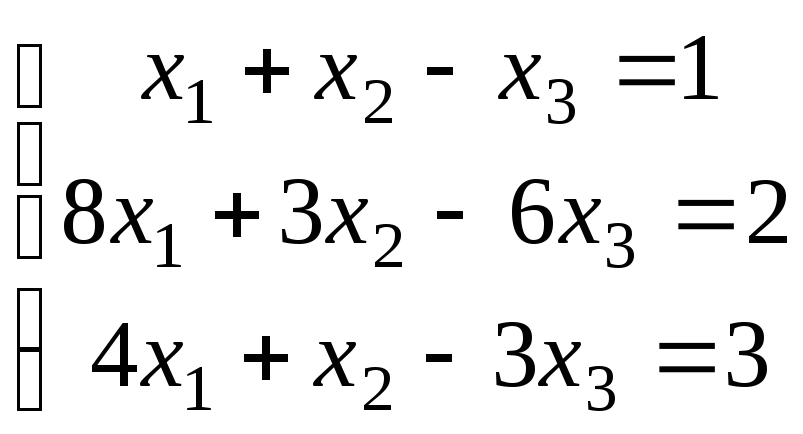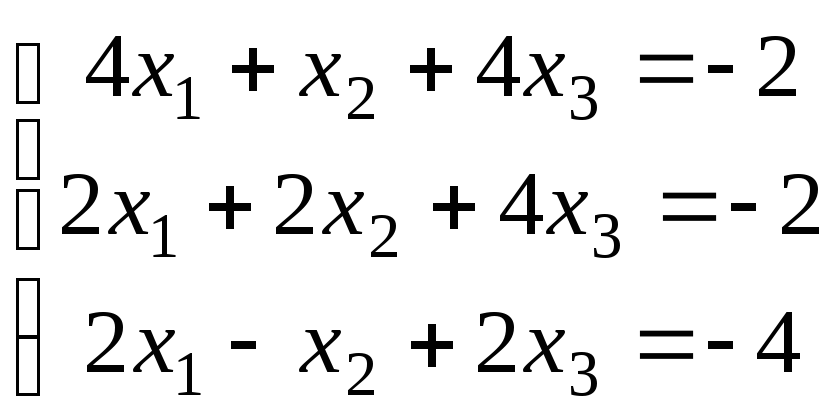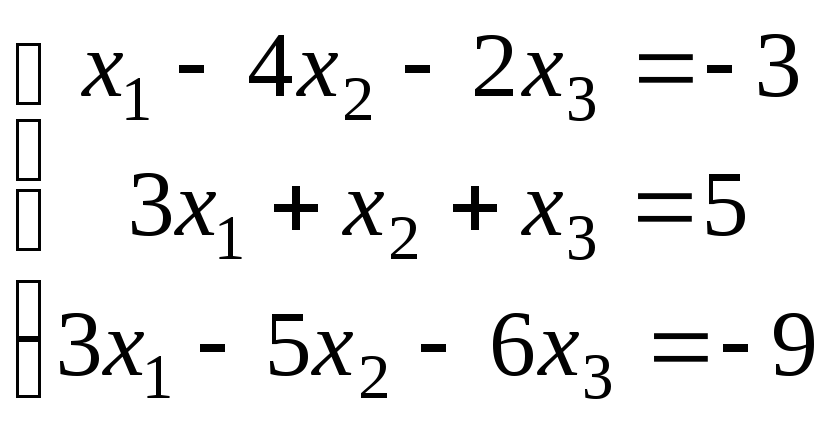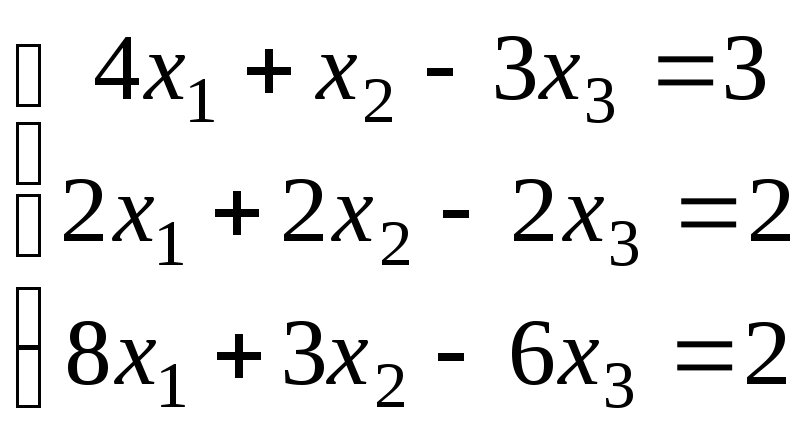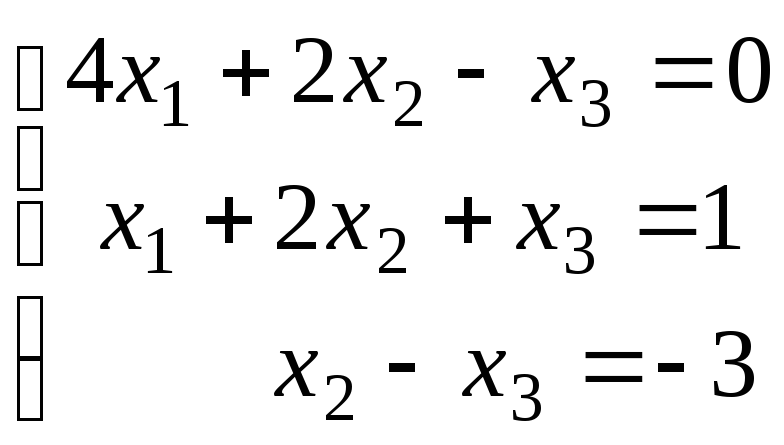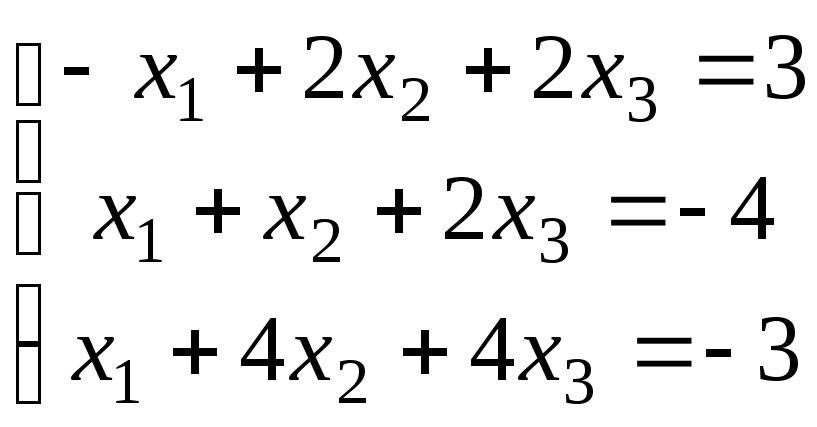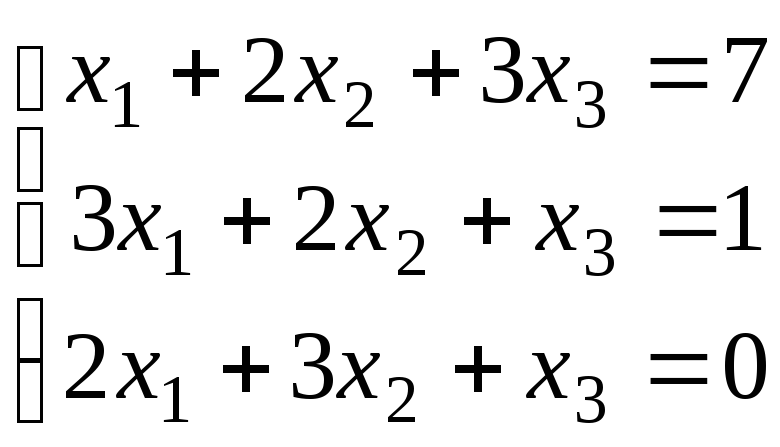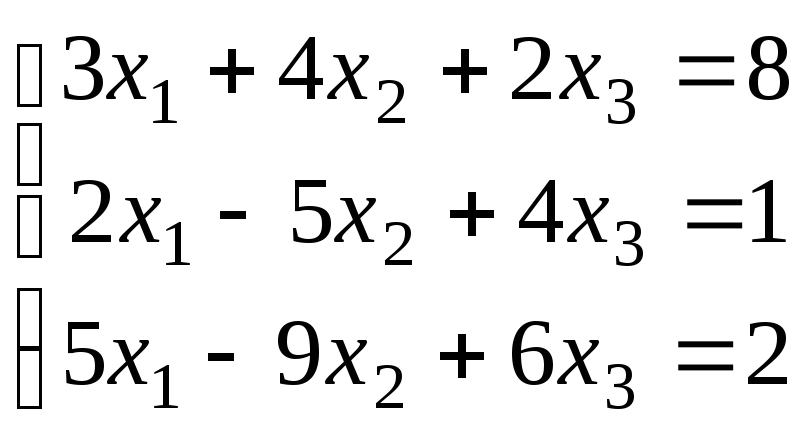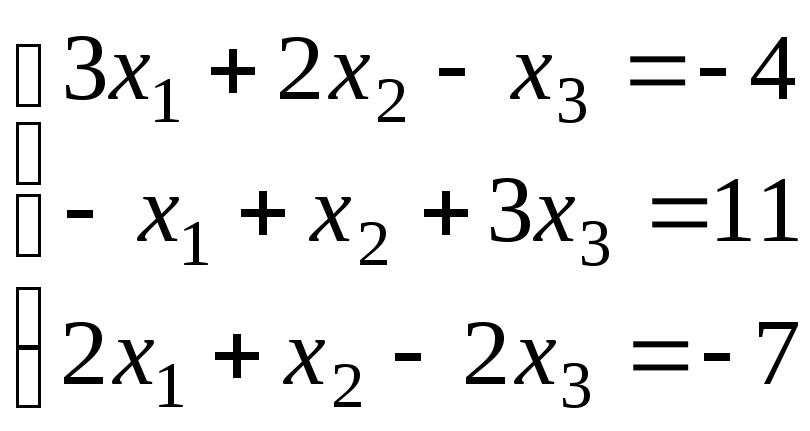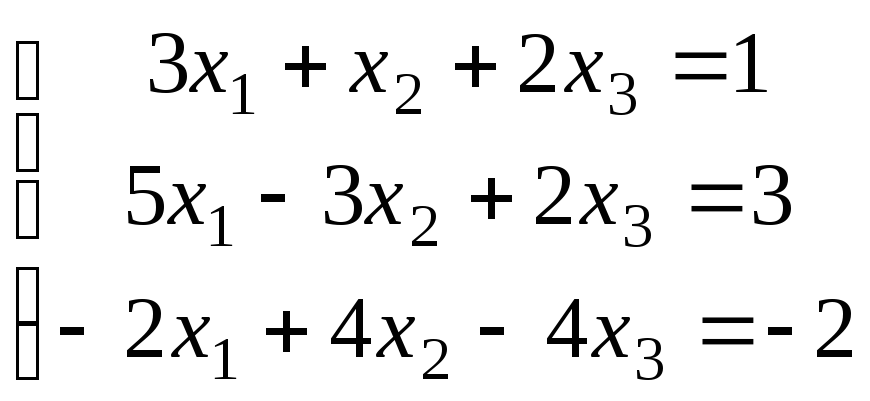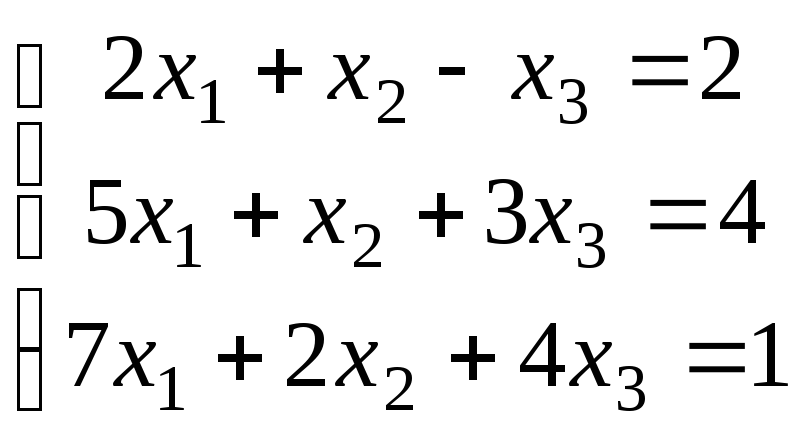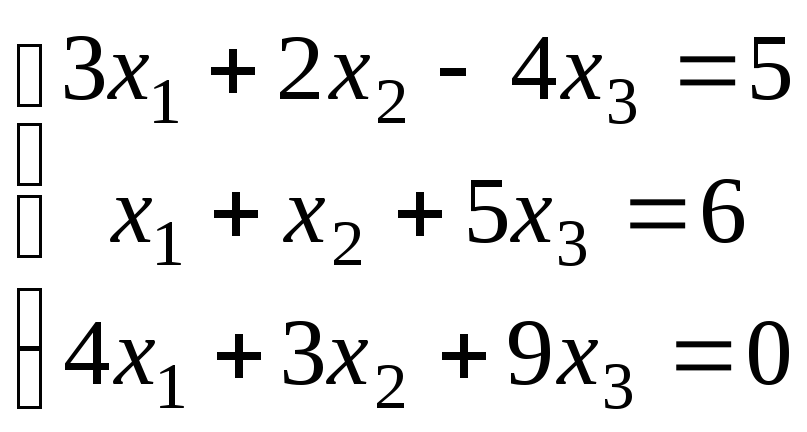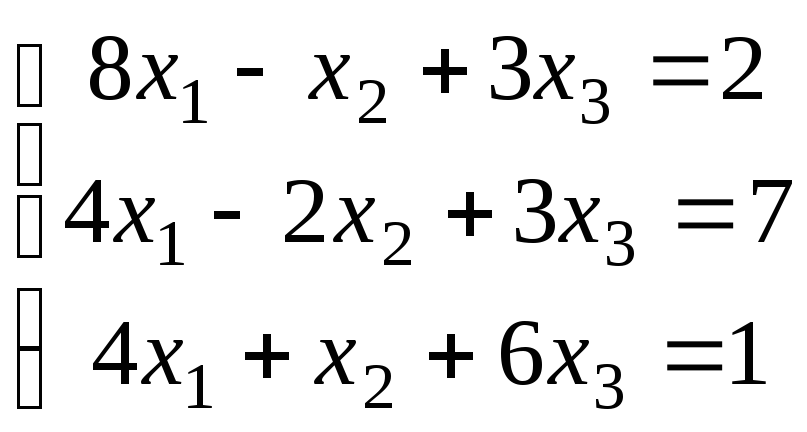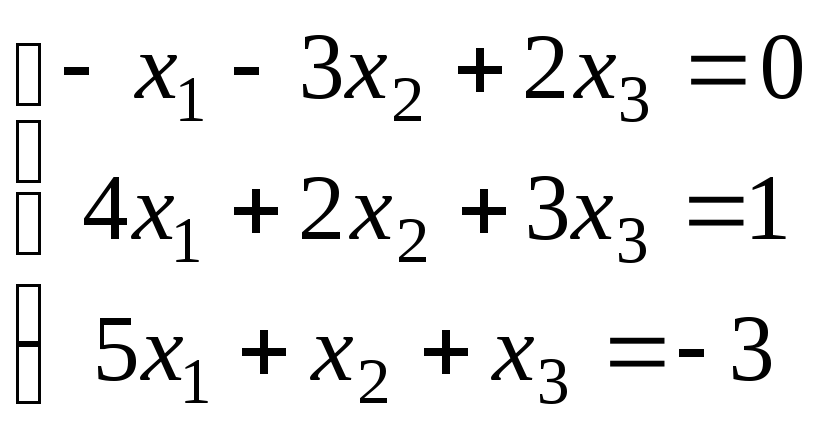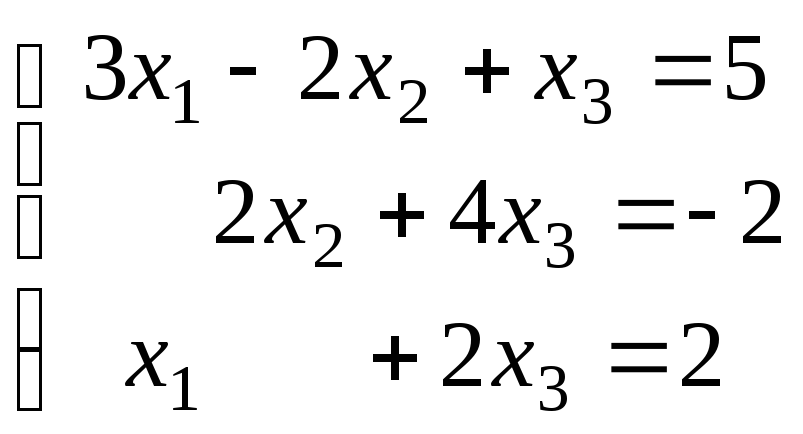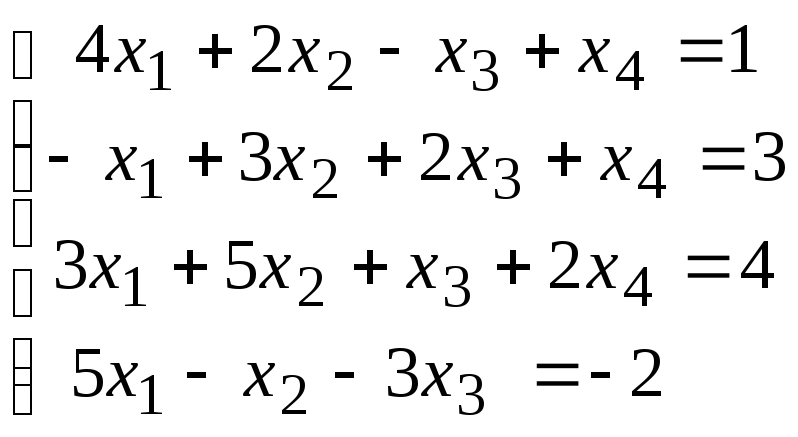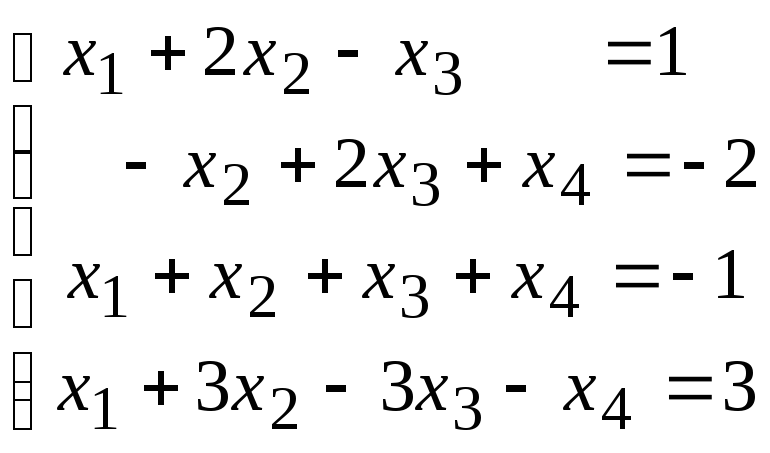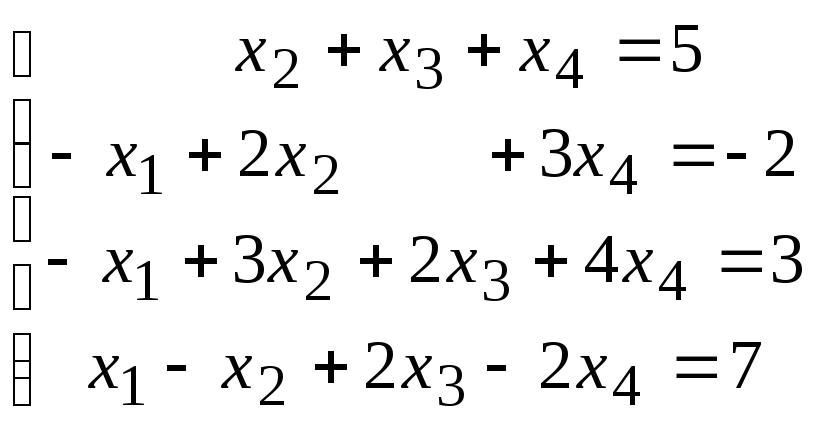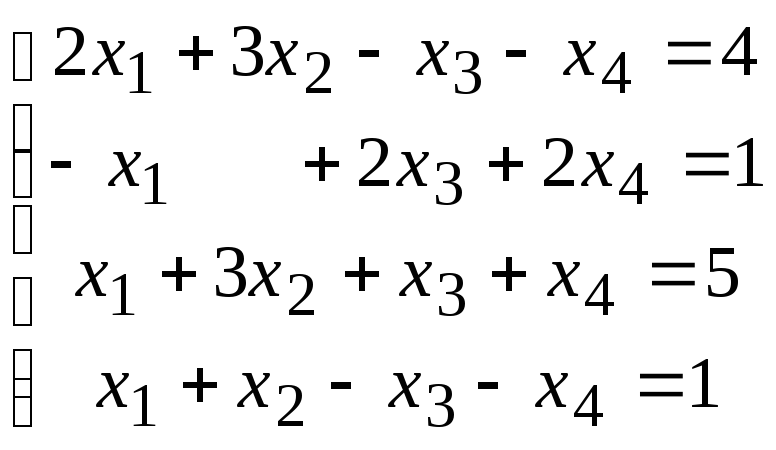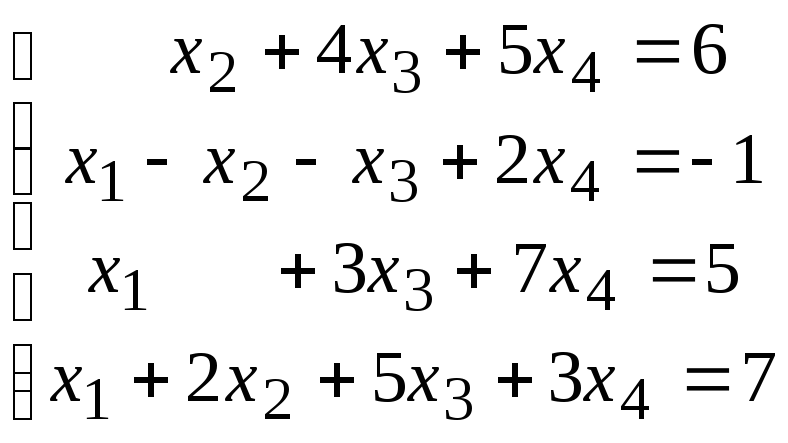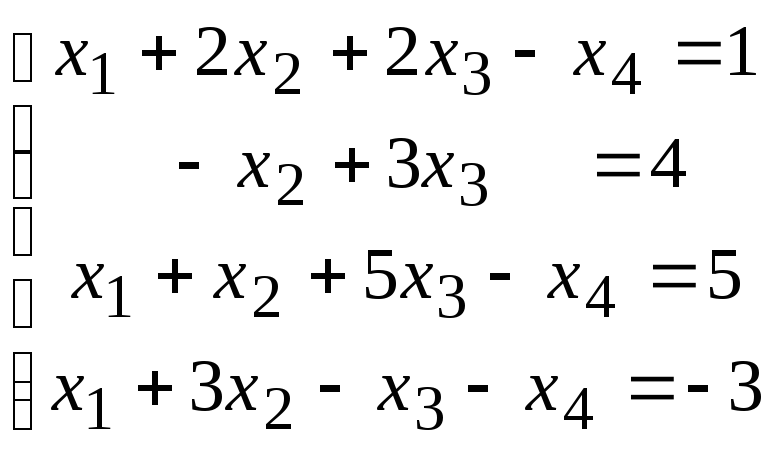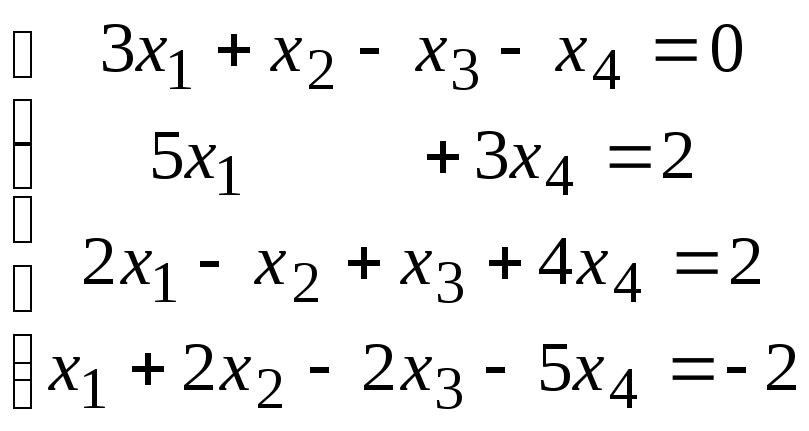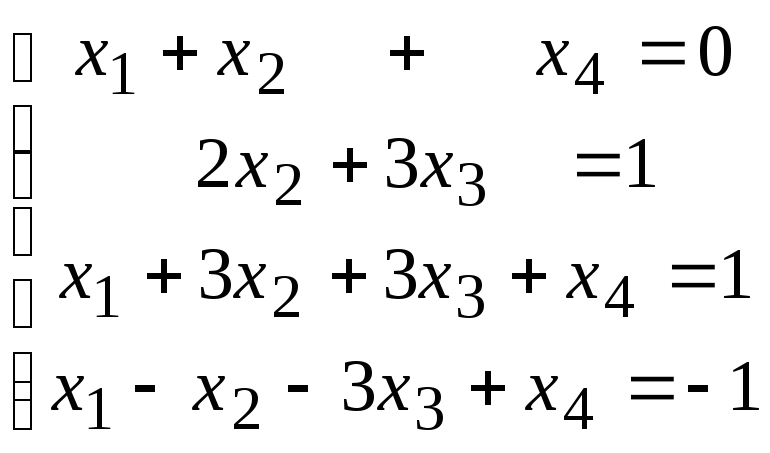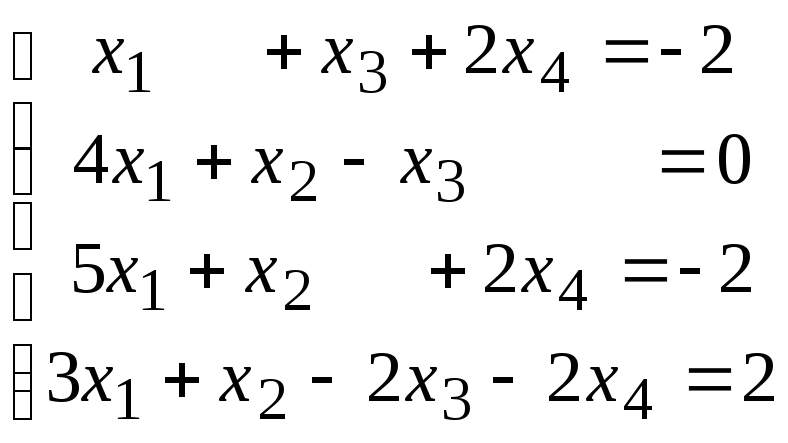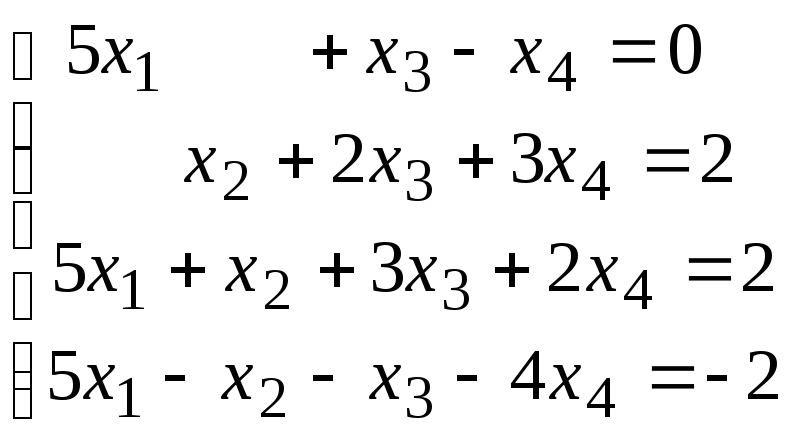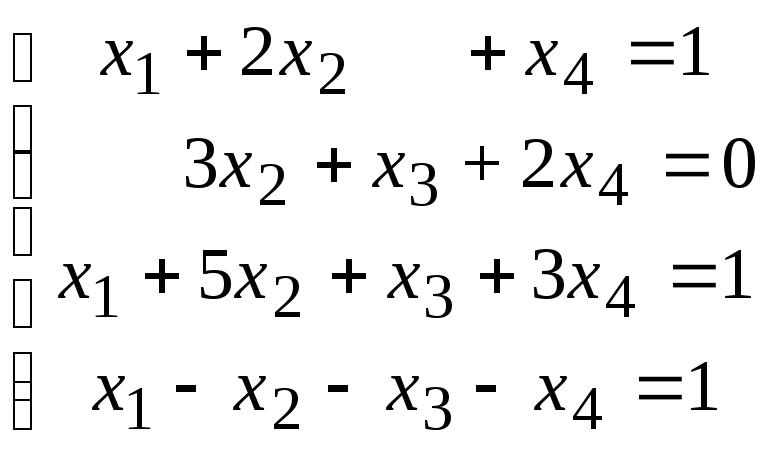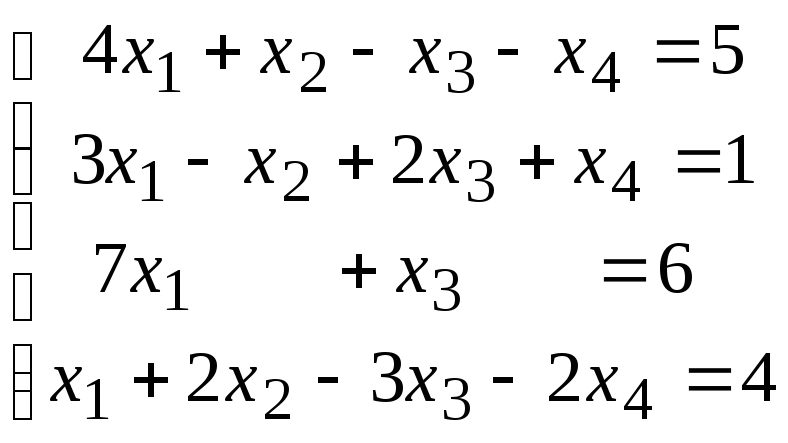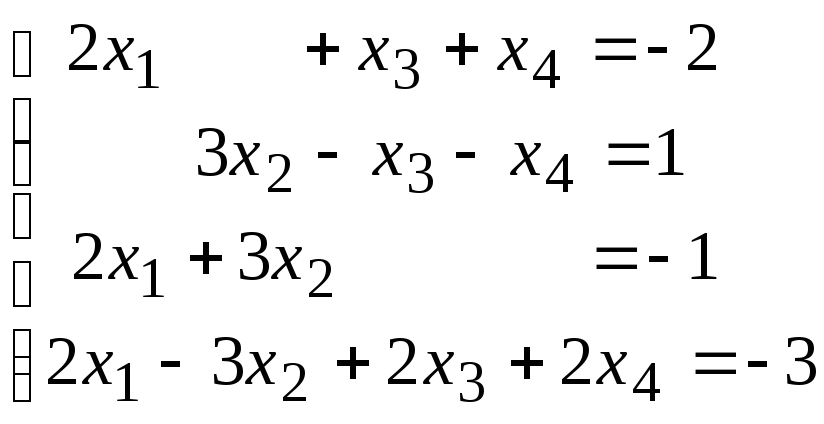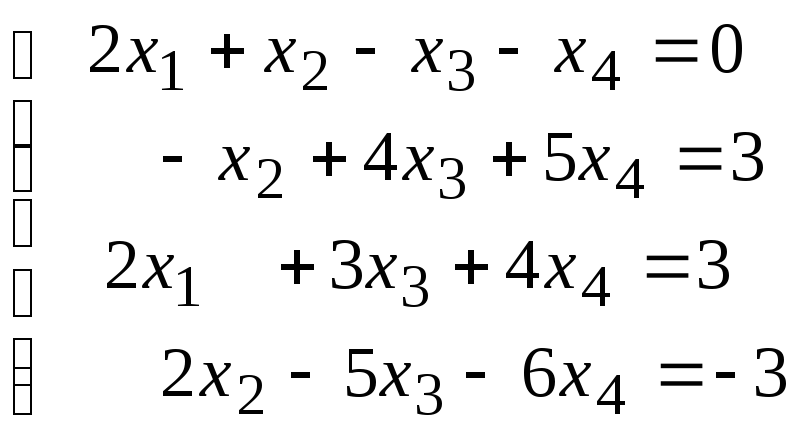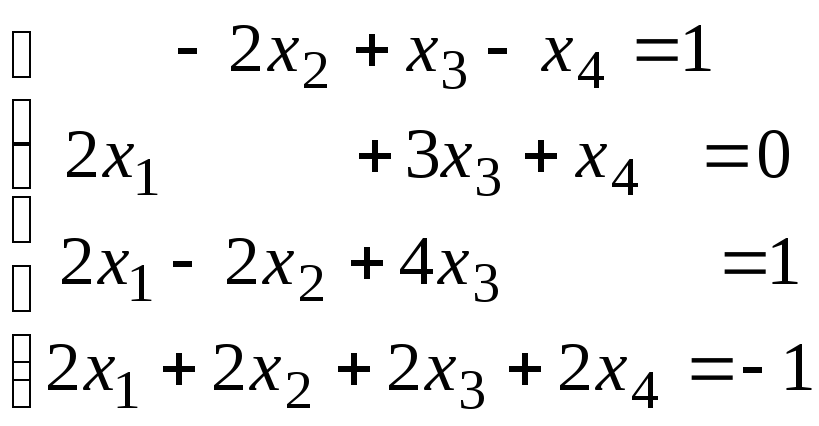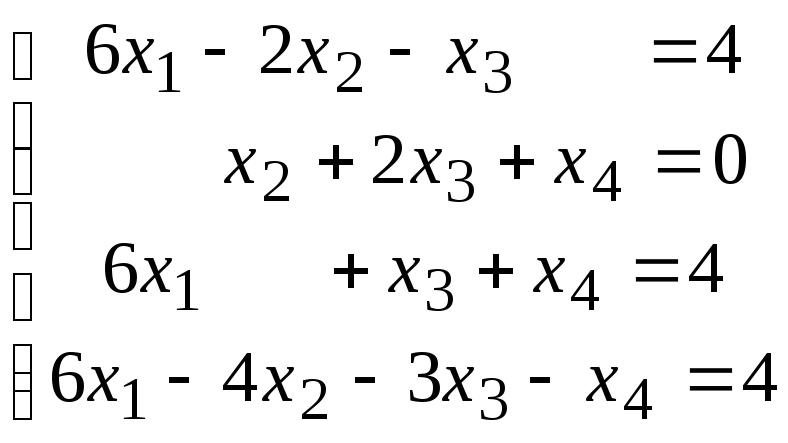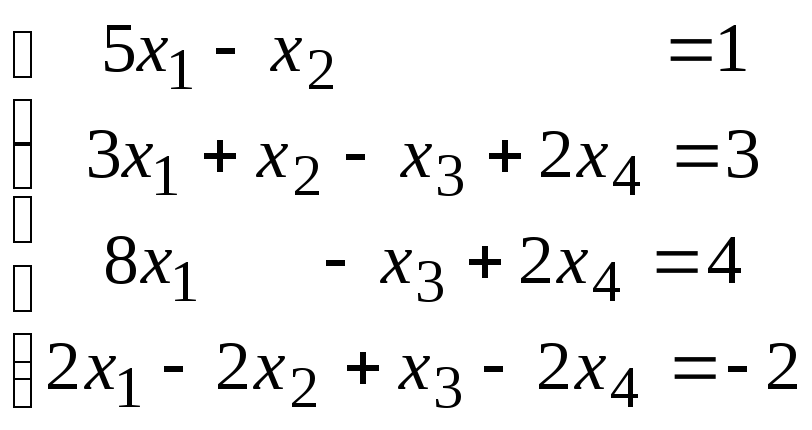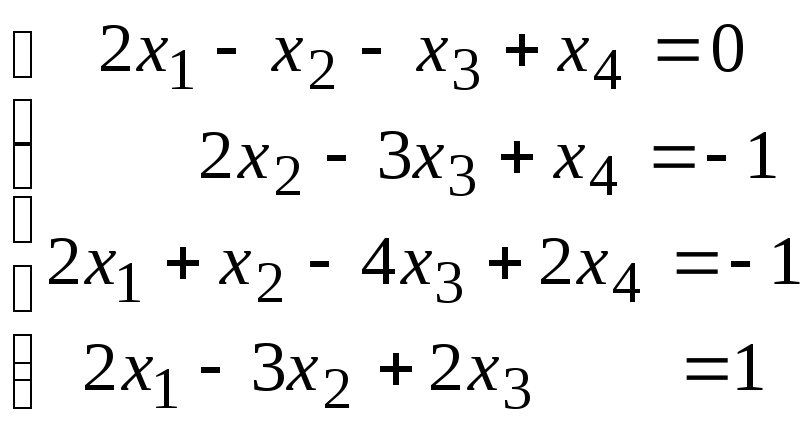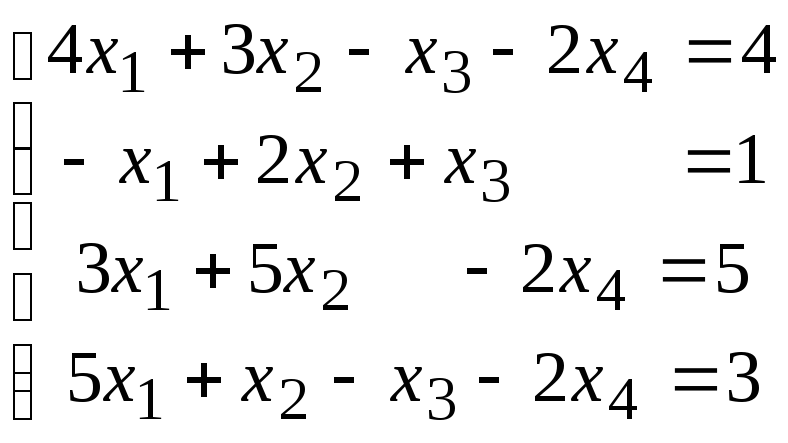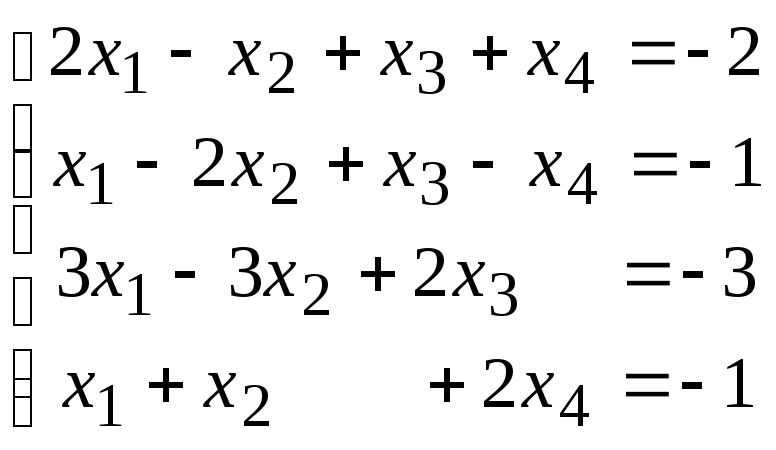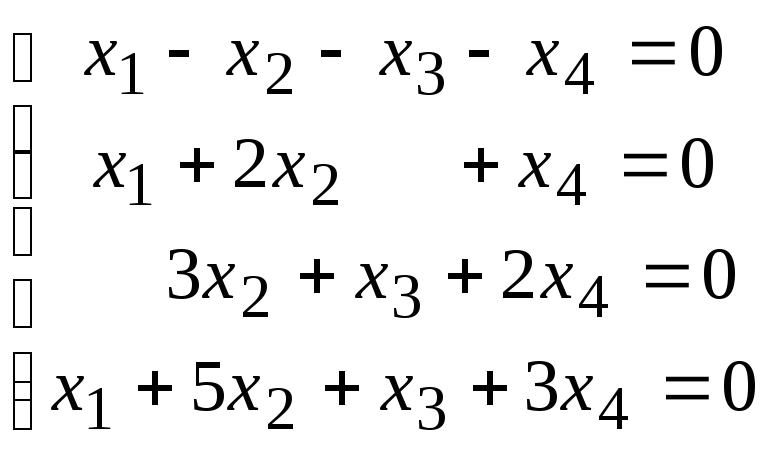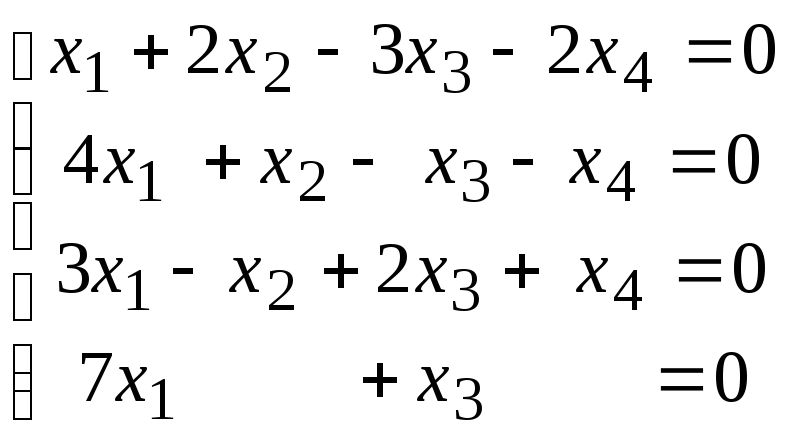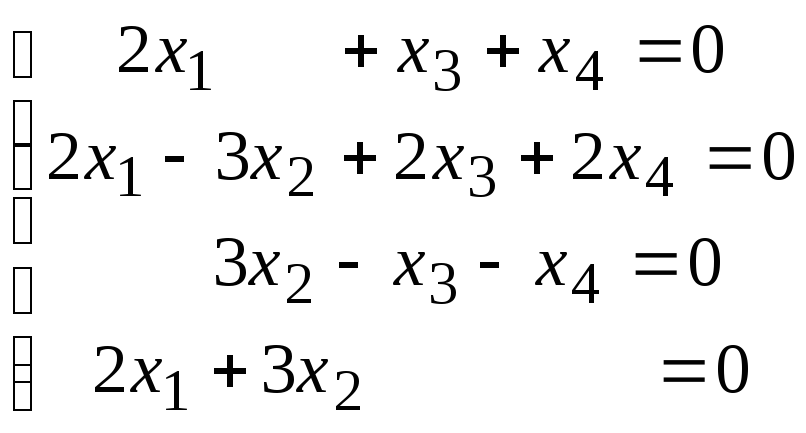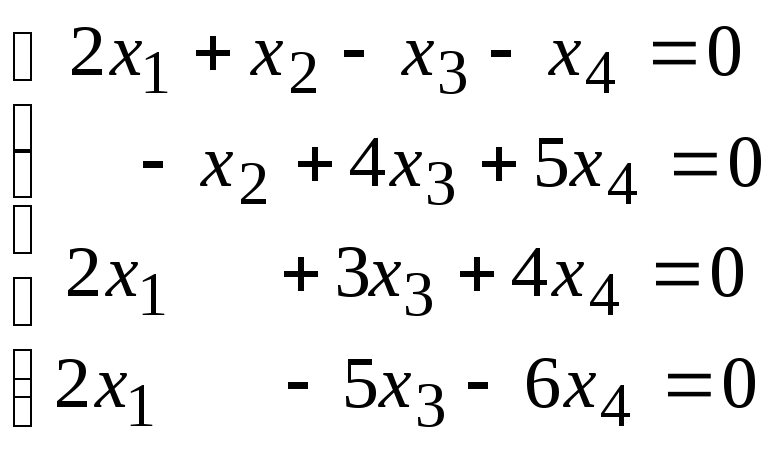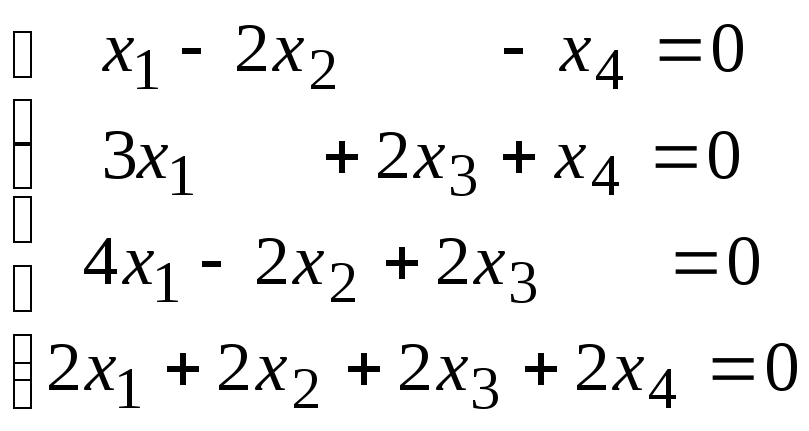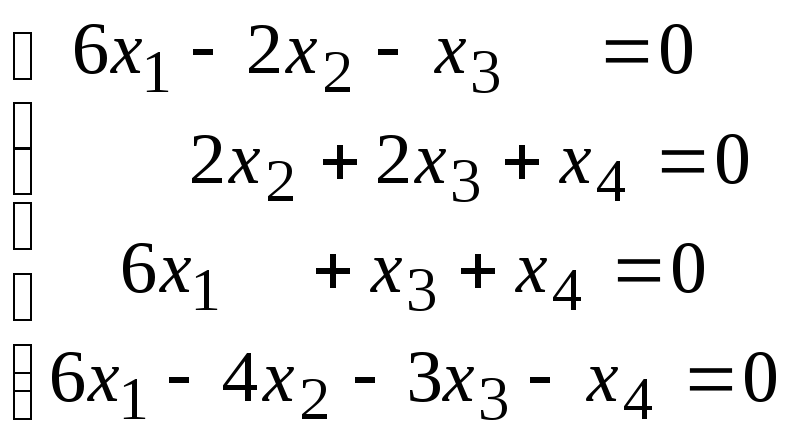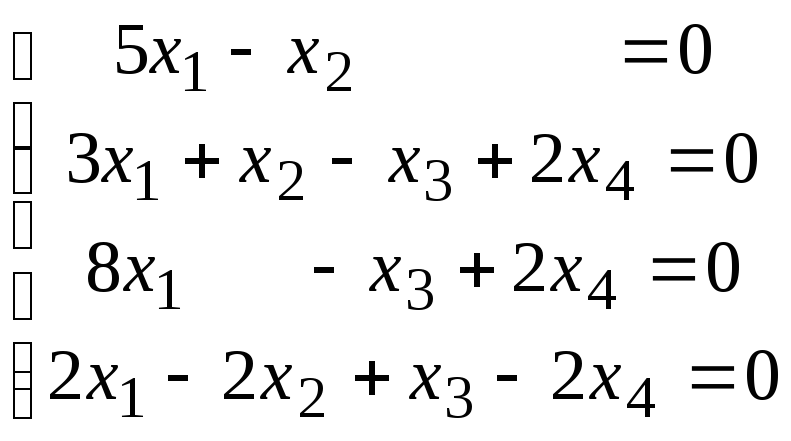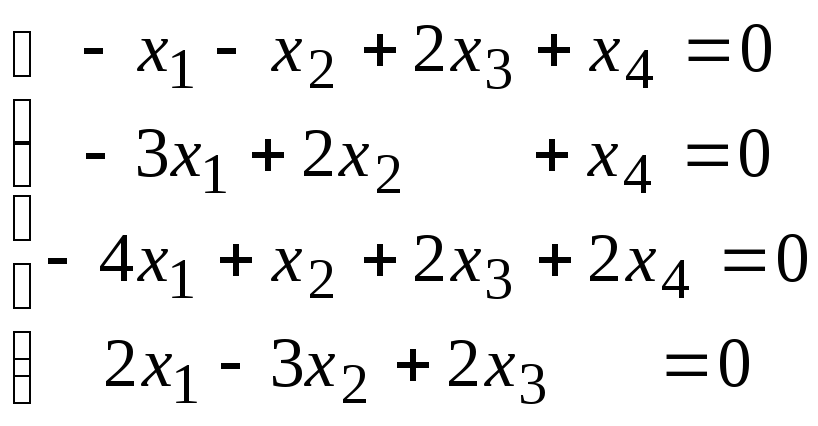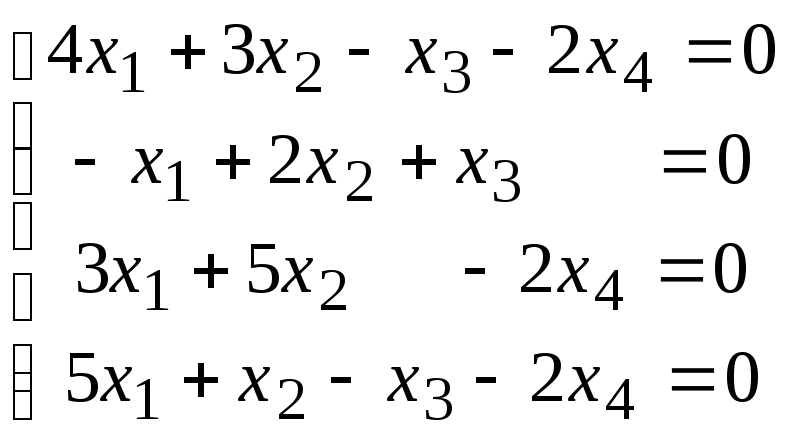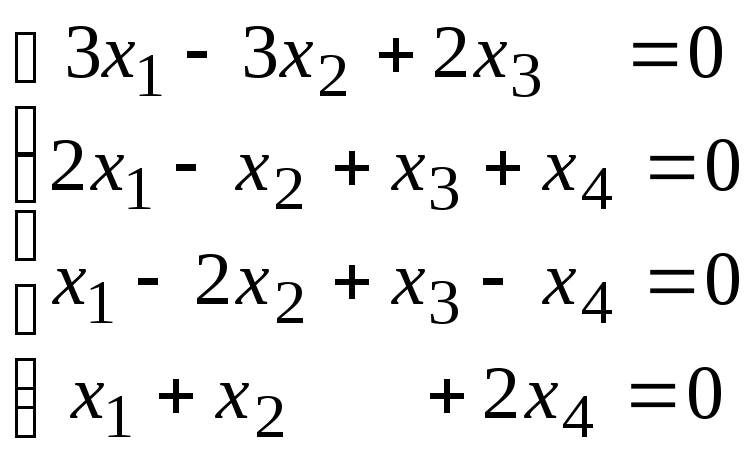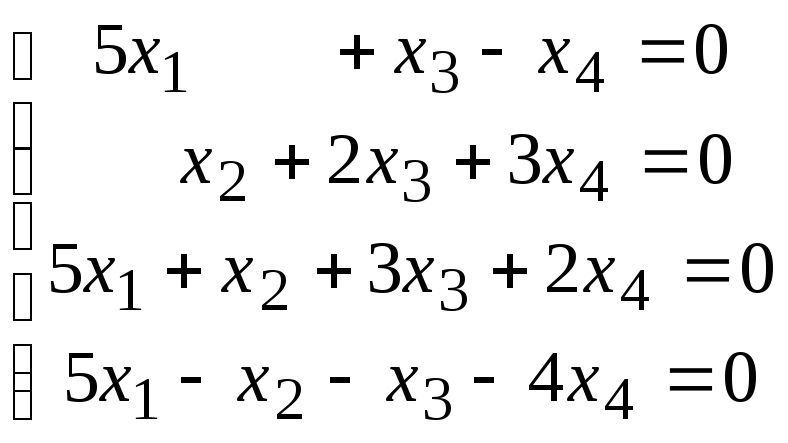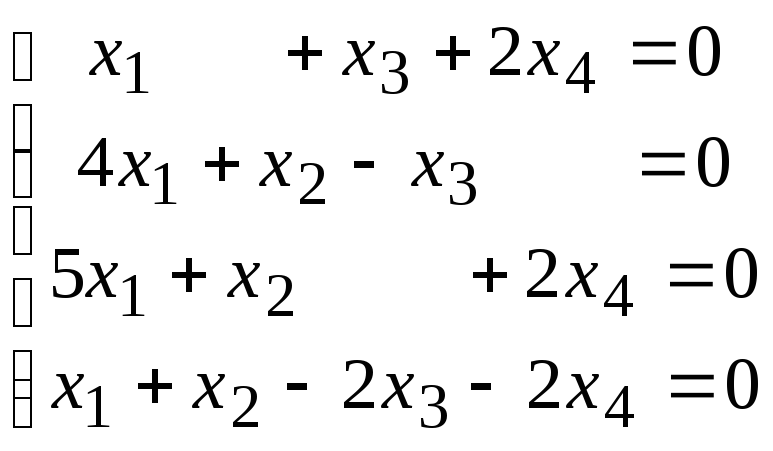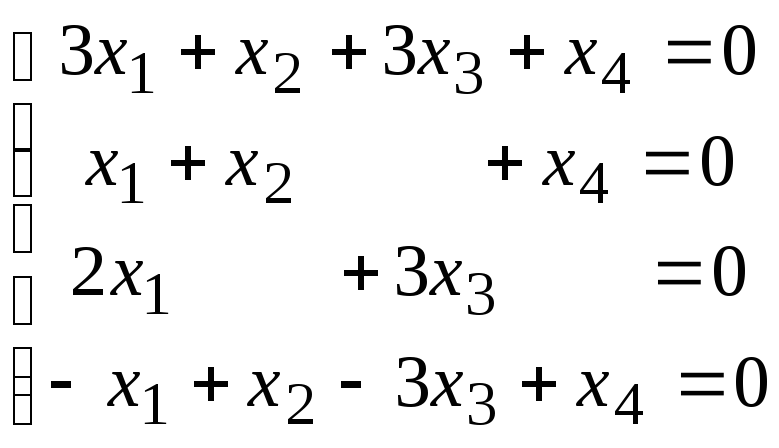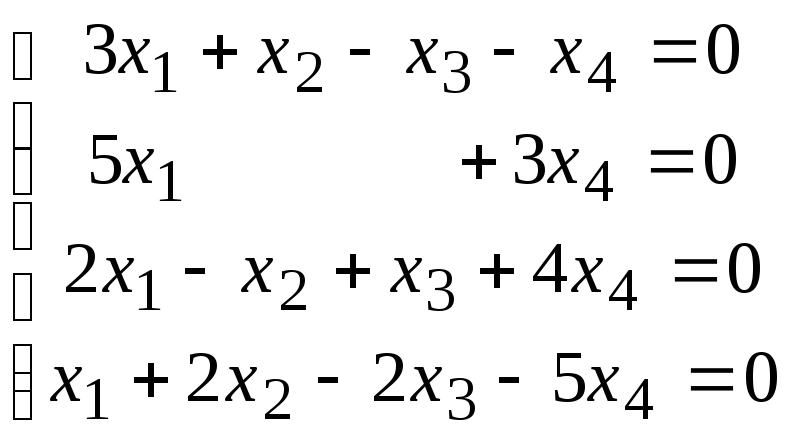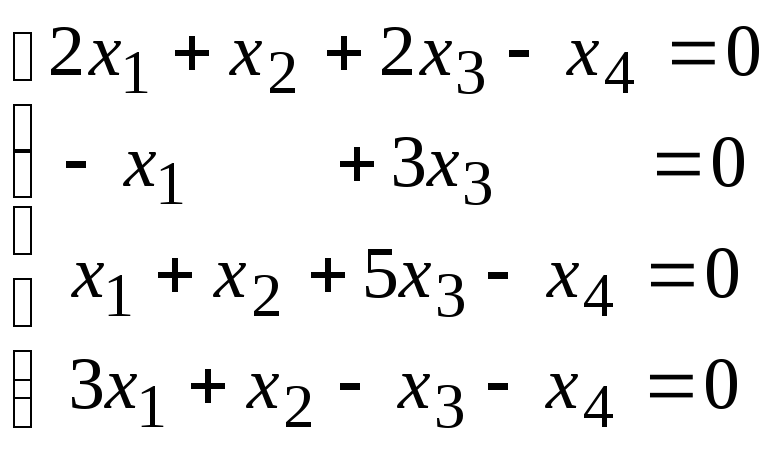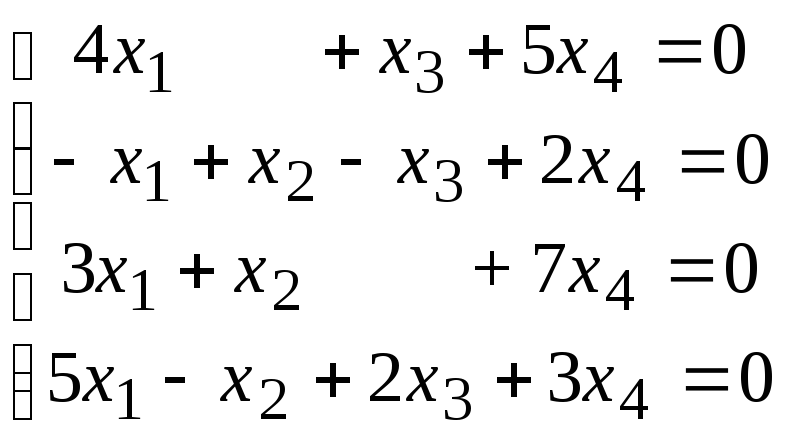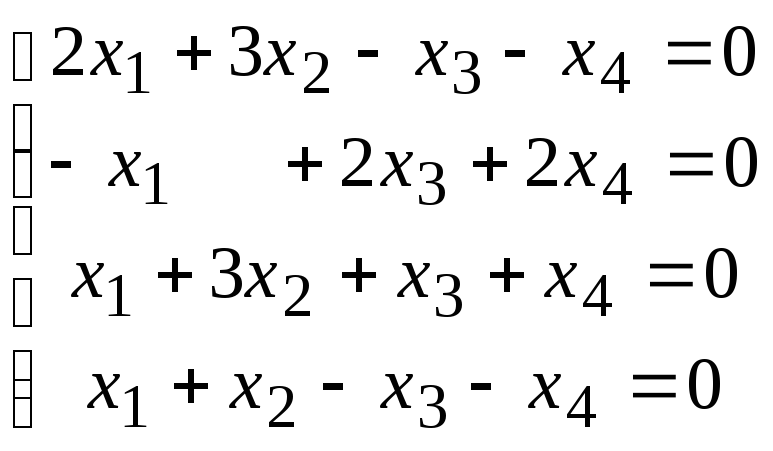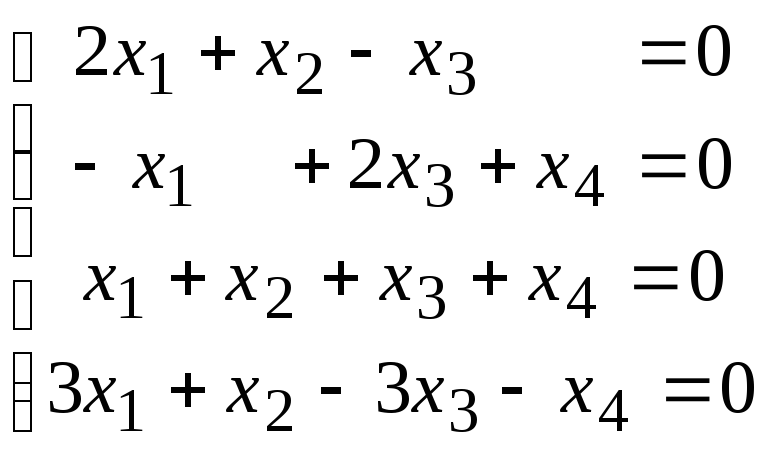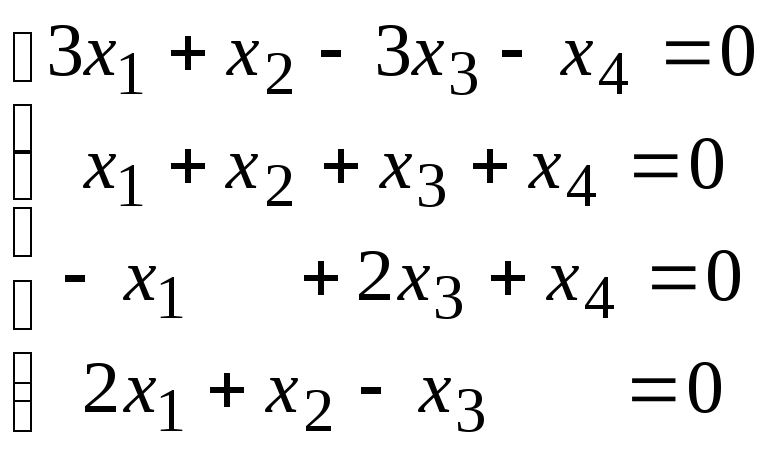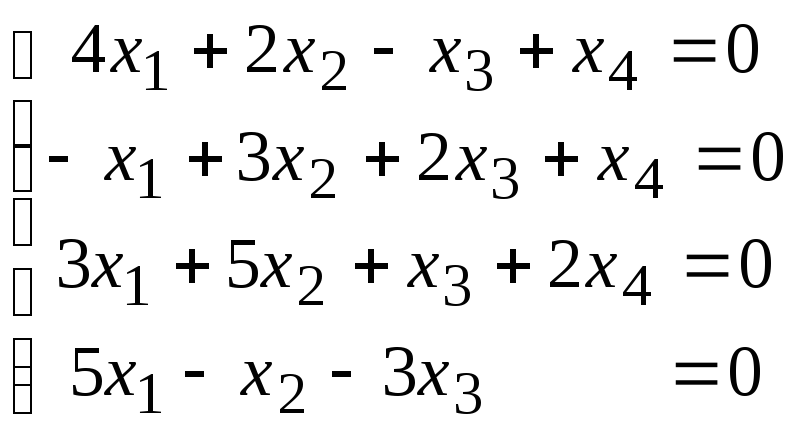Все работы по ИД МАТАНУ FAIT1 / MATRICA
.docИндивидуальное задание по линейной алгебре
(номер задания соответствует номеру варианта, например, для варианта №3 нужно решить задачи 1.3, 2.3, 3.3, и т.д., а для варианта №12 – задачи 1.12, 2.12, 3.12, и т.д.)
Задача 1.
Решить матричное уравнение относительно неизвестной матрицы Х , если А, В, С, D, E - заданные матрицы:
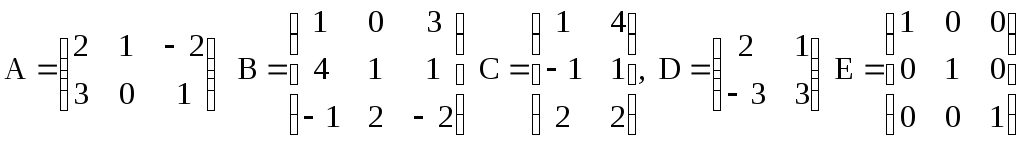
|
1.1. А·В+2·СТ =3·Х |
1.2. (В·Е)2 +С·А = 4·ХТ |
|
1.3. D2 – 3·A·C = 2·XT |
1.4. 4·(D·A)T + C = 4·X |
|
1.5.
(B·C)T
+ 2·A
=
|
1.6.
C·A
– 2·BT
=
|
|
1.7. 2·B2 + AT·CT = E·X |
1.8. B·AT – 3·C = 5·X |
|
1.9. (A·B)T – 3·C = X |
1.10. (B–E)T = C·A + 2·X |
|
1.11. A·B + 2·X = CT |
1.12. 4·D2 + X = (A·C)T |
|
1.13. (E·B)2 - 4·XT = 2·C·A |
1.14. 3·C - 5·X = B·AT |
|
1.15. –XT = 2·A·C - D2 |
1.16. (E - B)T + 4·C·A = –XT |
|
1.17. X·E + 4·A·B = CT |
1.18. 3·C – 5·X = B·AT |
|
1.19. B·AT – 2·X = E·C |
1.20. AT·CT – 3·B2 = X·E |
Задача 2.
Доказать, что данная система линейных уравнений имеет единственное решение. Найти решение двумя способами: 1) по формулам Крамера; 2) с помощью обратной матрицы. Сделать проверку.
|
2.1.
|
2.2.
|
|
2.3.
|
2.4.
|
|
2.5.
|
2.6.
|
|
2.7.
|
|
|
2.9.
|
2.10.
|
|
2.11.
|
|
|
2.13.
|
|
|
2.15.
|
|
|
2.17.
|
|
|
2.19.
|
2.20.
|
Задача 3.
Методом исключения (методом Гаусса) исследовать совместность системы линейных уравнений и найти все ее решения.
|
3.1.
|
|
|
|
|
|
3.5.
|
3.6.
|
|
3.7.
|
3.8.
|
|
3.9.
|
3.10. |
|
3.11.
|
3.12.
|
|
3.13.
|
3.14.
|
|
3.15.
|
|
|
3.17.
|
|
|
3.19.
|
3.20.
|
Задача 4.
Задана однородная система линейных уравнений. Требуется:
а) доказать, что система имеет нетривиальное решение;
б) найти базис пространства решений (фундаментальную систему решений);
в) записать общее решение и какое-либо частное решение.
|
4.1.
|
|
|
4.3.
|
|
|
4.5.
|
|
|
4.7.
|
|
|
4.9.
|
|
|
4.11.
|
|
|
4.13.
|
|
|
4.15.
|
|
|
4.17.
|
|
|
4.19.
|
4.20.
|