Метод замены переменных в определенном интеграле

Метод замены переменной в определенном интеграле имеет некоторые отличия от соответствующего метода в неопределенном интеграле.

Пусть требуется вычислить , гдеf(x) непрерывная на [a,b] функция. Алгоритм замены переменной таков.

1. Выбрать замену (заменяющую или заменяемую функцию):

2. Найти новые пределы интегрирования ииз условия

() =а,() =b,

или, соответственно,=(а),=(b).

3. Преобразовать подынтегральное выражение f(x)dxс помощью этой замены к видуg(t)dt.

.

4. Вычислить полученный интеграл

= .

Отличие от замены переменной в неопределенном интеграле состоит в том, что, получив искомую первообразную, не нужно возвращаться к старой переменной. Но при этом в процессе замены переменной интегрирования обязательноменяются пределы интегрирования.

Замечание. Функции-замены обязательно должны быть непрерывны на соответствующем промежутке. Например, для вычисления интеграла подстановкуприменить можно, так как на отрезкеэта функция непрерывна, а для вычисления интеграла– нельзя, т.к. в точкех =  функция имеет бесконечный разрыв.

Пример 7. Вычислить, используя метод замены переменных:

а) ; б) ; в) ;

г) ;д); е).

Решение.

а) Вычислим . Заданная подынтегральная функция является иррациональной, поэтому воспользуемся рекомендациями по подбору подстановки (файл «3.Замена переменной (метод подстановки), таблица 5).

Очевидно, это случай 2.1 таблицы 5, следовательно, необходимо заменить х на :

.

б) Выполним в данном интеграле подстановку :

.

в) Прежде всего, заметим, что подынтегральная функция – четная, поэтому используем упрощение вычисления

.

Используем тригонометрическую подстановку (случай 2.6 таблицы 5):

.

Тогда .

г) Для вычисления от тригонометрической функции используем универсальную подстановку (таблица 6, 3.1):

.

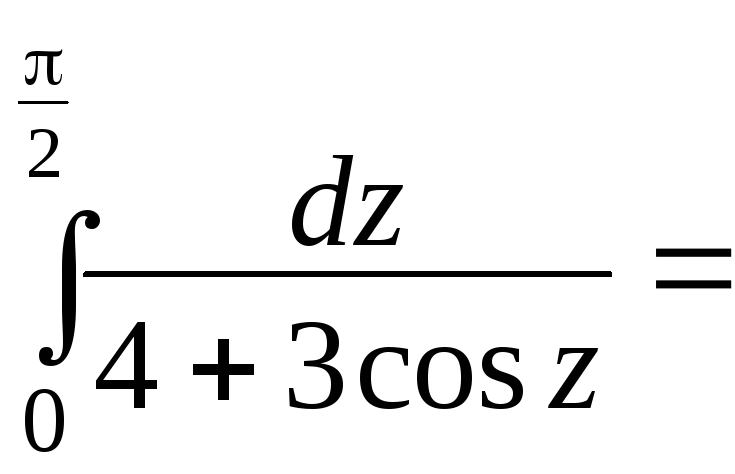
д) В интеграле удобнее воспользоваться частной подстановкой (случай 3.1.1. таблицы 6):

.

Заметим, что здесь (α+1) – константа, поэтому этот коэффициент вынесен за знак интеграла.

Получили интеграл от рациональной дроби. Поскольку дискриминант знаменателя положительный и «удобный» для вычисления корней , разложим эту дробь на простейшие дроби:

Тогда . Теперь имеем

.

е) Преобразуем

.

Метод интегрирования по частям в определенном интеграле

Метод интегрирования по частям в определенном интеграле основан на формуле

.

Все рекомендации по выбору функций и и dv, указанные для неопределенного интеграла, остаются в силе (файл «Интегрирование по частям»).

Пример 8. Вычислить, используя метод интегрирования по частям:

а) ; б) ;

в) ; г);

д) ; е).

Решение.

а) Напомним рекомендации: если подынтегральное выражение имеет вид

, ,,

где Р(х) – многочлен, то за и берется многочлен Р(х), – всё остальное – за dv. В заданном интеграле подынтегральное выражение относится к одному из этих классов, поэтому делаем соответствующий выбор:

.

б) Учитывая упомянутые выше рекомендации, получим

.

в) При вычислении воспользуемся рекомендациями:если интеграл имеет вид

, ,,

, ,,,

то за и берется логарифмическая или обратная тригонометрическая функция, а .

Тогда получим

г) Учитывая рекомендации из пункта в), получим

д) Действуем аналогично предыдущему:

.

е) Здесь также воспользуемся рекомендациями из пункта в). Получим

.

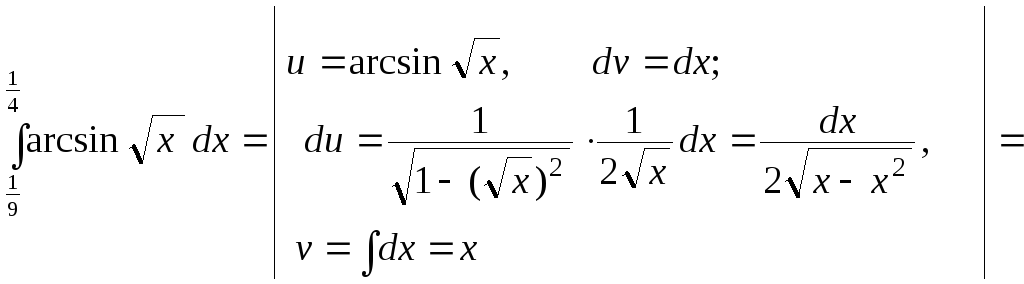
*⁾ Функция называется периодической с периодомТ, если выполняется условие:

для любого х из области определения этой функции.

*^*) Длину отрезка находят по правилу:.