FAIT1 / Интегралы-Помощь / Определенный интеграл / 2. Несобственные интегралы
.docНесобственный интеграл
Определенный интеграл как предел интегральной суммы
может существовать (т.е. иметь определенное конечное значение) лишь при выполнении условий
-
отрезок интегрирования [a; b] конечный;
-
подынтегральная функция
непрерывная (или хотя бы кусочно-непрерывная)
и, следовательно, ограниченная на этом
отрезке.
Если
хотя бы одно из этих условий нарушено,
то определение теряет смысл. Действительно,
в случае бесконечного отрезка, например
[a;
)
его нельзя разбить на п
частей конечной длины
,
которая к тому же с увеличением количества
отрезков стремилась бы к нулю. В случае
же неограниченной в некоторой точке
с[a;
b]
нарушается требование произвольного
выбора точки
на частичных отрезках – нельзя выбрать
=с,
поскольку значение функции в этой точке
не определено. Однако и для этих случаев
можно обобщить понятие определенного
интеграла, введя еще один предельный
переход. Интегралы по бесконечным
промежуткам и от разрывных (неограниченных)
функций называют несобственными.
Определение.
Пусть
функция
определена на промежутке [a;
)
и интегрируема на любом конечном отрезке
[a;
b],
т.е. существует
для любого b
> a.
Предел вида
называют несобственным
интегралом
первого
рода (или
несобственным интегралом по бесконечному
промежутку) и обозначают
.
Таким
образом, по определению,
=
.
Если
предел справа существует и конечен, то
несобственный интеграл
называют сходящимся.
Если этот предел бесконечен, или не
существует вообще, то говорят, что
несобственный интеграл расходится.
Аналогично
можно ввести понятие несобственного
интеграла от функции
по промежутку (–;
b]:
=
.
А
несобственный интеграл от функции
по промежутку (–;
+)
определяется как сумма введенных выше
интегралов:
=
+
,
где а – произвольная точка. Этот интеграл сходится, если сходятся оба слагаемых, и расходится, если расходится хотя бы одно из слагаемых.
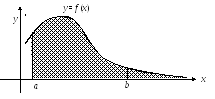С
геометрической точки зрения, интеграл
,
,
определяет численное значение площади
бесконечной криволинейной трапеции,
ограниченной сверху графиком функции
,
слева – прямой
,
снизу – осью ОХ. Сходимость интеграла
означает существование конечной площади
такой трапеции и равенство ее пределу
площади криволинейной трапеции с
подвижной правой стенкой
.
На случай интеграла с бесконечным пределом можно обобщить и формулу Ньютона-Лейбница:
=
=
F(+)
– F(a),
где
F(+)
=
.
Если этот предел существует, то интеграл
сходится, в противном случае – расходится.
Мы рассмотрели обобщение понятия определенного интеграла на случай бесконечного промежутка.
Рассмотрим теперь обобщение для случая неограниченной функции.
Определение
Пусть
функция
определена на промежутке [a;
b),
неограниченна в некоторой окрестности
точки b,
и непрерывна на любом отрезке
,
где >0
(и, следовательно, интегрируема на этом
отрезке, т.е.
существует). Предел вида
называется несобственным
интегралом второго рода
(или несобственным интегралом от
неограниченной функции) и обозначается
.
Таким образом, несобственный интеграл от неограниченной в точке b функции есть по определению
=
.
Если предел справа существует и конечен, то интеграл называется сходящимся. Если конечного предела не существует, то несобственный интеграл называется расходящимся.
Аналогично
можно определить несобственный интеграл
от функции
имеющей бесконечный разрыв в точке а:
=
.
Если
функция
имеет бесконечный разрыв во внутренней
точке с
,
то несобственный интеграл определяется
следующим образом
=
+
=
+
.
Этот интеграл сходится, если сходятся оба слагаемых, и расходится, если расходится хотя бы одно слагаемое.
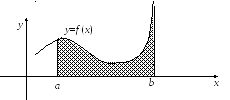С
геометрической точки зрения, несобственный
интеграл от неограниченной функции
также характеризует площадь неограниченной
криволинейной трапеции:
Поскольку несобственный интеграл выводится путем предельного перехода из определенного интеграла, то все свойства определенного интеграла могут быть перенесены (с соответствующими уточнениями) на несобственные интеграла первого и второго рода.
Во многих задачах, приводящих к несобственным интегралам, не обязательно знать, чему равен этот интеграл, достаточно лишь убедиться в его сходимости или расходимости. Для этого используют признаки сходимости. Признаки сходимости несобственных интегралов:
1) Признак сравнения.
Пусть
для всех х
.
Тогда, если
сходится, то сходится и
,
причем
.
Если
расходится, то расходится и
.
2)
Если сходится
,
то сходится и
(последний интеграл в этом случае
называется абсолютно
сходящимся).
Признаки сходимости и расходимости несобственных интегралов от неограниченных функций аналогичны сформулированным выше.
Примеры решения задач.
Пример 1.
Вычислить несобственный интеграл или установить его расходимость:
а)
;
б)
;
в)
г)
; д)
.
Решение.
а) По определению имеем:
,
Следовательно,
данный интеграл сходится и равен
.
б) Аналогично
.
Следовательно,
данный интеграл сходится и равен
.
в)
По определению
=
+
,
причем, а
– произвольное число. Положим в нашем
случае
,
тогда получим:
.
Данный интеграл сходится.
г)
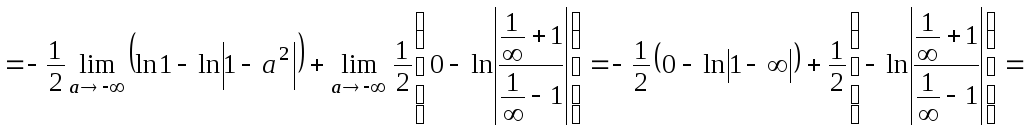
Значит, данный интеграл расходится.
д)
Рассмотрим
.
Чтобы найти первообразную подынтегральной
функции, необходимо применить метод
интегрирования по частям. Тогда получим:
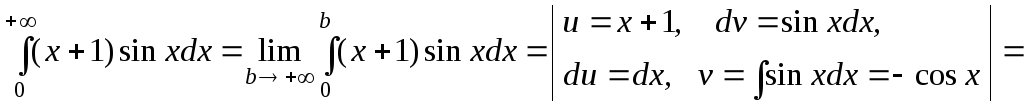
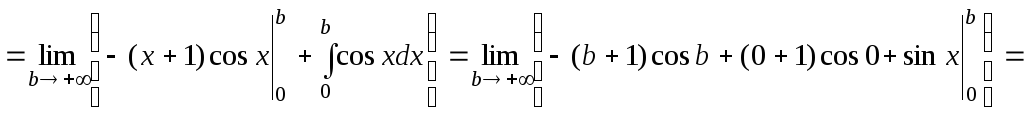
Поскольку
ни
,
ни
не существуют, то не существует и
.
Следовательно, данный интеграл расходится.
Пример 2.
Исследовать
сходимость интеграла
в зависимости от п.
Решение.
При
имеем:
.
Если
,
то
и
.
Следовательно, интеграл расходится.
Если
,
то
,
а
,
тогда
,
=
,
Следовательно, интеграл сходится.
Если
,
то
,
следовательно, интеграл расходится.
Таким
образом,
Пример 3.
Вычислить несобственный интеграл или установить его расходимость:
а)
;
б)
;
в)
.
Решение.
а)
Интеграл
является несобственным интегралом
второго рода, поскольку подынтегральная
функция
не ограничена в точке
.
Тогда, по определению,
.
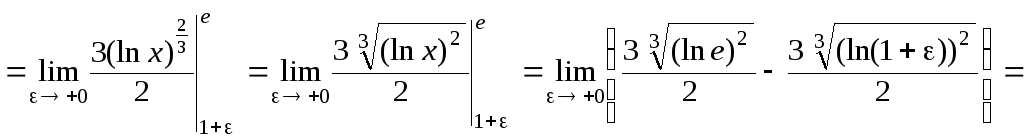
Интеграл сходится и равен
.
б)
Рассмотрим
.
Здесь также подынтегральная функция
не ограничена в точке
.
Поэтому, данный интеграл – несобственный
второго рода и по определению,
.
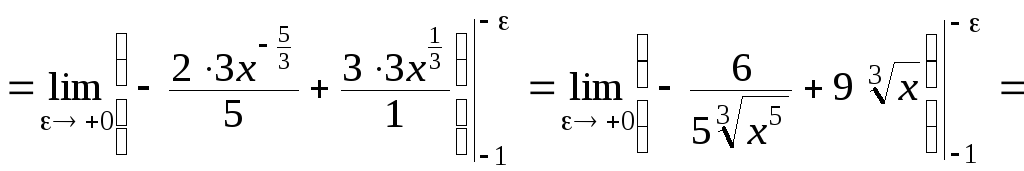
Следовательно, интеграл расходится.
в)
Рассмотрим
.
Подынтегральная функция
терпит бесконечный разрыв в двух точках:
и
,
первая из которых принадлежит промежутку
интегрирования
.
Следовательно, данный интеграл –
несобственный второго рода. Тогда, по
определению
=
=
.
Следовательно,
интеграл сходится и равен
.