
FAIT1 / Интегралы-Помощь / 2 .Интегрирование по частям
.docИнтегрирование по частям
Метод интегрирования по частям основан на формуле:
Формула применяется чаще всего в тех случаях, когда подынтегральная функция представляет собой произведение алгебраической и трансцендентной функции*). При этом за функцию и выбирается та из функций-сомножителей, которая при дифференцировании упрощается, а за dv выбирается та часть подынтегрального выражения, которая легко интегрируется.
При выборе функции и и дифференциала dv можно пользоваться следующими рекомендациями:
А) Если интеграл имеет вид
![]() ,
,
![]() ,
,
![]() ,
,
где Р(х) – многочлен, то за и берется многочлен Р(х), – всё остальное – за dv;
В) Если интеграл имеет вид
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
то за и
берется логарифмическая
или обратная
тригонометрическая функция,
а
![]() .
.
Пример 1. Найти интегралы:
а)
![]() ;
б)
;
б)
![]() ;
;
в)![]() г)
г)![]() .
.
Решение.
а) Используя рекомендации А, применим формулу интегрирования по частям:
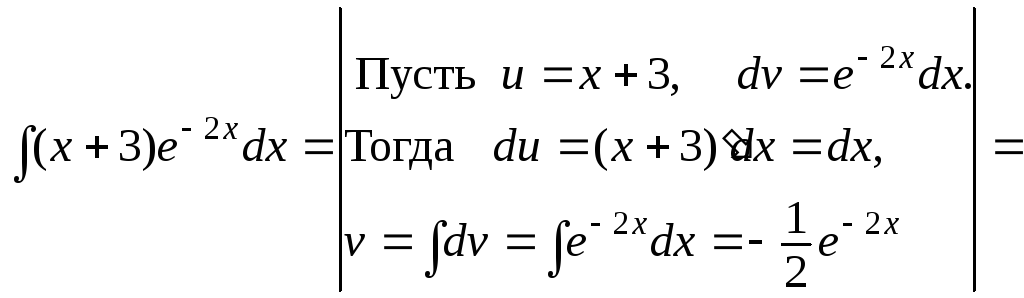
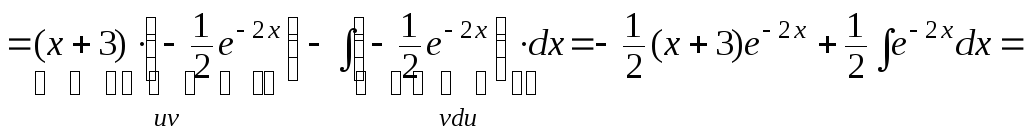
![]() .
.
Здесь использована формула 5 таблицы 1.
Заметьте также, что при отыскании функции v , хоть и записывается неопределенный интеграл, но рассматривается только одна из возможных первообразных (т.е. сразу полагается С=0).
б)

![]()
![]() .
.
Здесь использованы формулы 6а и 7а таблицы 1.
в)

![]() .
.
Здесь использованы формулы 6а и 7а таблицы 1, а так же тот факт, что
![]() .
.
г) Формулу интегрирования по частям можно применять несколько раз. При этом каждый раз выбор функции и и дифференциала dv производится заново, в соответствии в получившимся интегралом. Найденную на предыдущем шаге часть первообразной uv, необходимо сохранять до конца вычислений:



![]()
![]()
![]()
![]()
![]() .
.
Пример 2. Найти интегралы:
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() .
.
Решение.
а) Воспользуемся рекомендациями В):

=
![]()
![]()
![]() .
.
б)

![]() .
.
в)

=![]()
![]() .
.
Пример 3. Найти интегралы:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)
![]() .
.
Решение.
а) Вновь воспользуемся рекомендациями В):
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
б)![]()
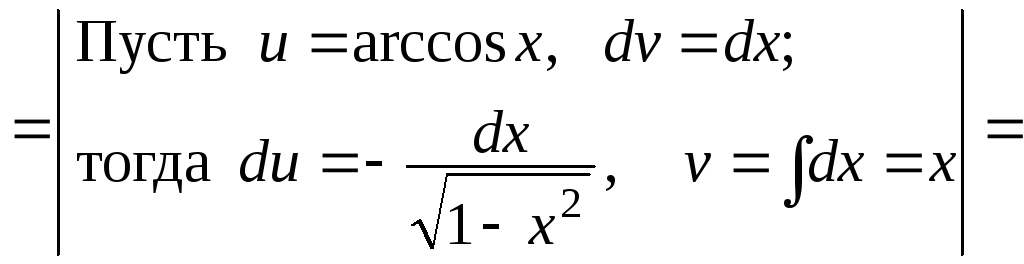
![]()

![]() .
.
в)![]()

![]()
![]() .
.
Пример 4. Найти интегралы:
а)
![]() ;
б)
;
б)![]() .
.
Решение.
а)
![]()
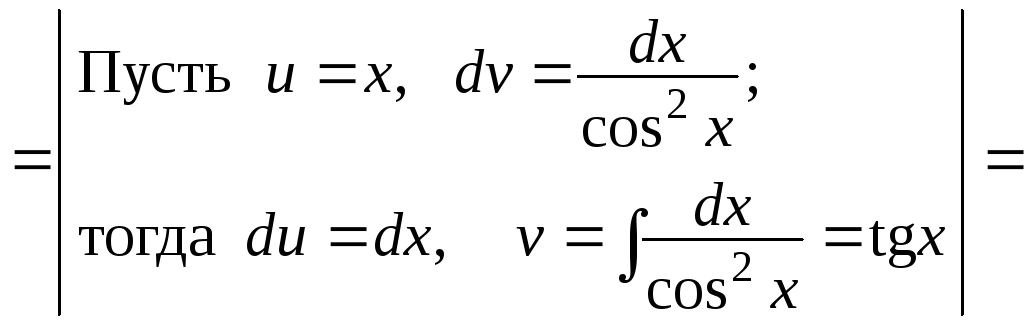
![]()
![]() .
.
б)![]() .
.

![]()

![]()
![]() .
.
*) Алгебраическими функциями являются многочлены, отношения многочленов, а также иррациональные функции. К трансцендентным функциям относят показательные, логарифмические, тригонометрические и обратные тригонометрические функции.
