
FAIT1 / Интегралы-Помощь / 4. Интегрирование рациональных дробей
.docИнтегрирование дробно-рациональных функций
(рациональных дробей)
Дробно-рациональной функцией (рациональной дробью) называют функцию вида
 .
.
Из линейной алгебры известно, что всякую правильную рациональную дробь можно разложить на сумму простейших дробей типа
-
I.
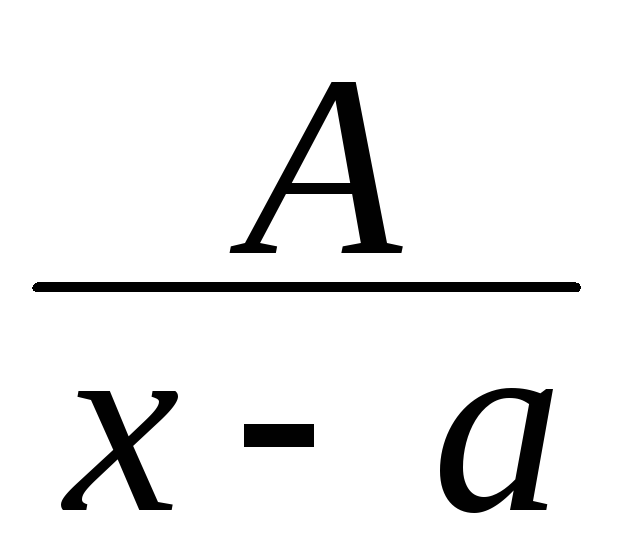 ( А,
а
– константы)
( А,
а
– константы)
-
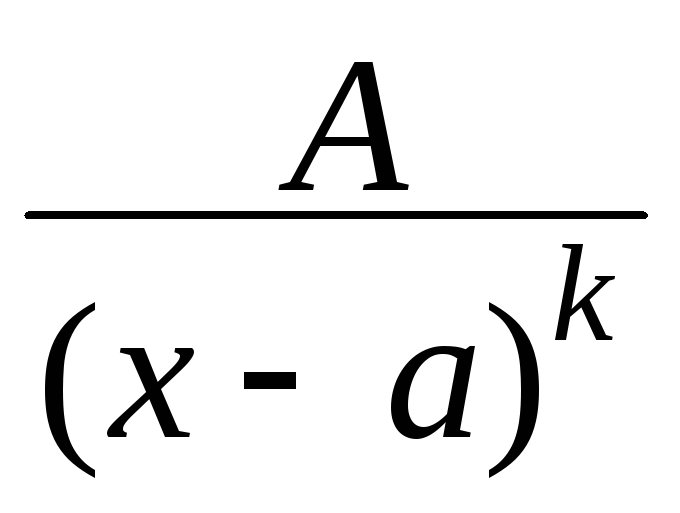 ,
( k
2 целое число)
,
( k
2 целое число)
-
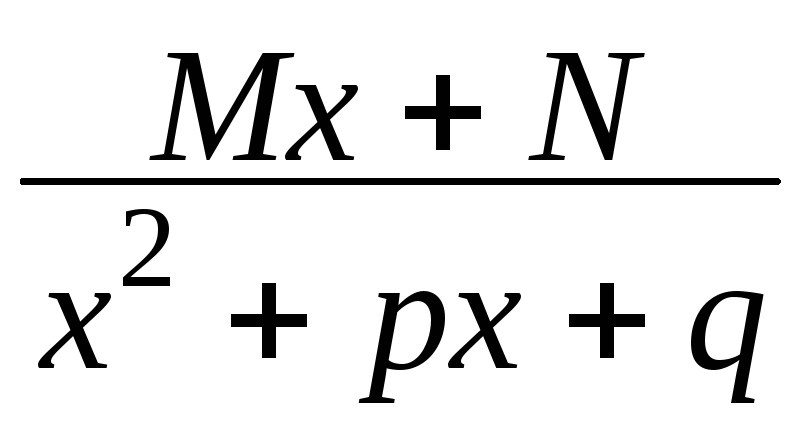 (М,
N,
p,
q
– константы, дискриминант знаменателя
меньше нуля)
(М,
N,
p,
q
– константы, дискриминант знаменателя
меньше нуля) -
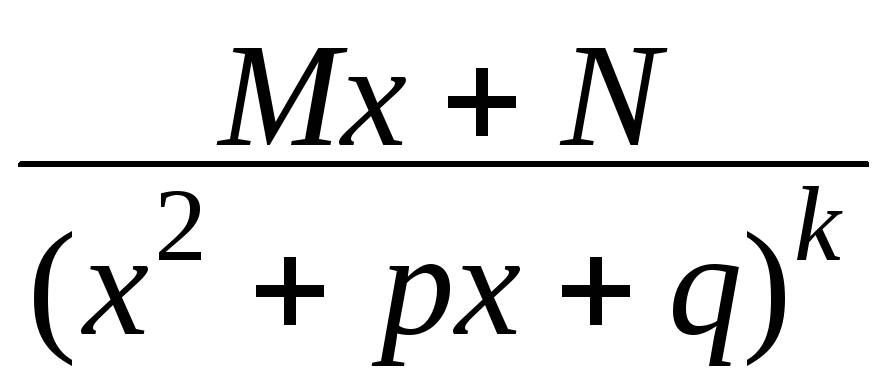 (
k
2 целое, знаменатель не имеет действительных
корней).
(
k
2 целое, знаменатель не имеет действительных
корней).
А всякую неправильную рациональную дробь можно представить в виде суммы многочлена (целой части) и правильной рациональной дроби.
Таким образом, интегрирование рациональной дроби может быть сведено к интегрированию многочлена и простейших дробей, перечисленных выше. Рекомендации по интегрированию простейших дробей мы рассматривали в теме «Замена переменной».
Напомним еще раз эти принципы:
Таблица 4. Рациональные функции
|
Вид интеграла |
Способ интегрирования |
|
1.1.
|
|
|
1.2.
|
|
|
1.3.
|
Выделение полного квадрата:
|
|
1.4.
|
Рекуррентная формула
|
Итак, алгоритм интегрирования рациональной дроби таков:
-
Выяснить, является ли дробь правильной. Если дробь неправильная, то разделив числитель на знаменатель, выделить целую часть:
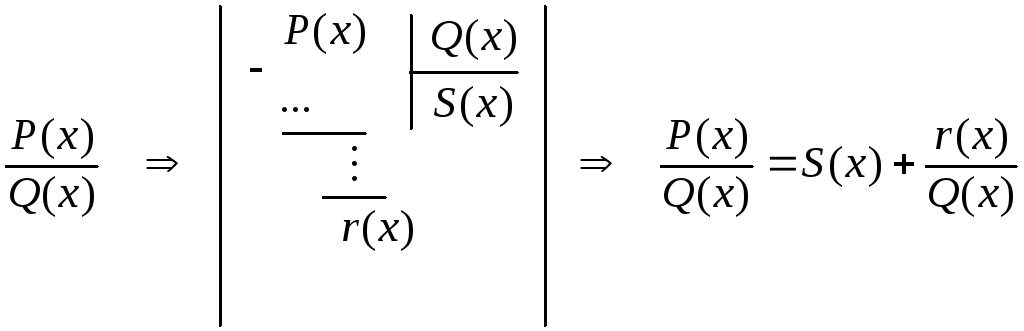
-
Знаменатель правильной дроби разложить на неприводимые множители вида
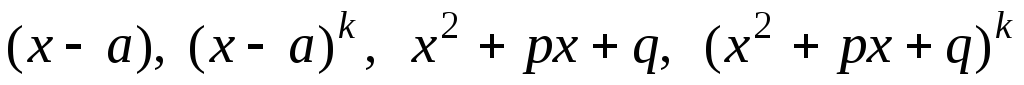 .
. -
Разложить правильную дробь на простейшие, записав в это разложение для каждого множителя дроби по принципу:
для
множителя
![]() в сумме записывается дробь
в сумме записывается дробь
![]() ;
;
для
множителя
![]() записывается сумма k
дробей
записывается сумма k
дробей
![]() ;
;
для
множителя
![]() записывается дробь
записывается дробь
![]() ;
;
для
множителя
![]() записывается сумма k
дробей
записывается сумма k
дробей
![]() .
.
-
Найти коэффициенты разложения и представить интеграл от заданной функции как интеграл от полученной суммы дробей.
-
Разложить интеграл от полученной суммы на сумму интегралов и вычислить каждый из интегралов-слагаемых.
Рассмотрим примеры.
Пример 1. Найти интегралы:
а)![]() ;
б)
;
б)![]() ;
в)
;
в)
![]() .
.
Решение.
а)
В интеграле
![]() подынтегральная функция есть правильная
рациональная дробь. Разложим ее на
простейшие дроби:
подынтегральная функция есть правильная
рациональная дробь. Разложим ее на
простейшие дроби:
![]()
![]()
![]()
Приравняем числители исходной и полученной дробей:
![]() .
.
Приравняем коэффициенты многочленов, стоящих в левой и правой частях этого равенства, получим:
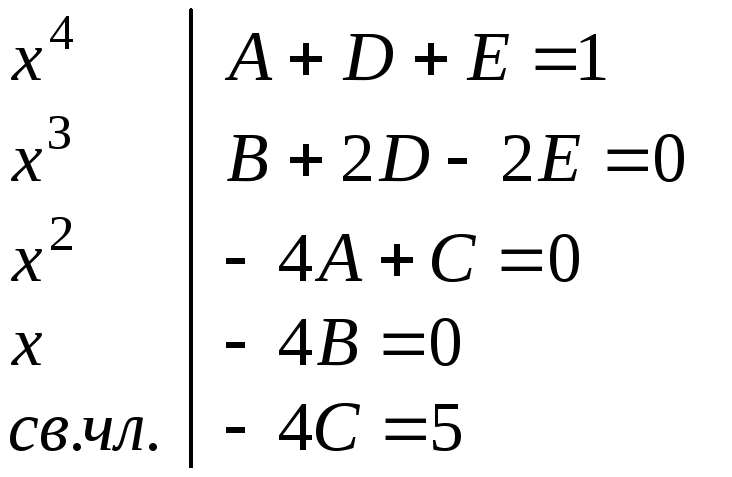
Получили систему уравнений относительно неизвестных коэффициентов разложения. Решая ее, находим:
![]()
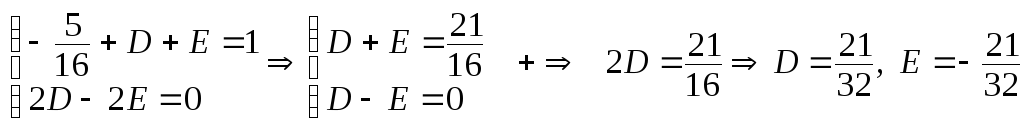
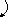 .
.
Тогда получим
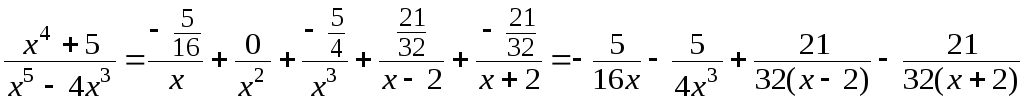 .
.
Интегрируем:
![]()
![]()
![]() .
.
б)
Дано:![]() .
Аналогично, разложим подынтегральную,
правильную, дробь на простейшие:
.
Аналогично, разложим подынтегральную,
правильную, дробь на простейшие:
![]()
![]() .
.
Приравняем числители исходной и полученной дробей:
![]() ,
,
![]() .
.
Приравнивая коэффициенты при одинаковых степенях переменной х, получим систему уравнений:
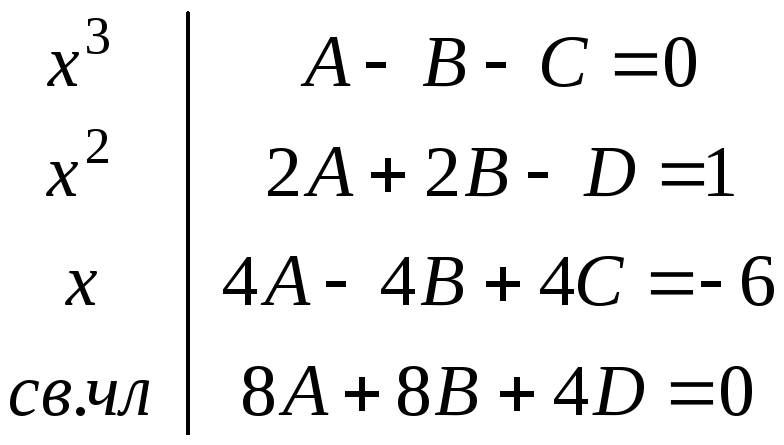
Умножим первое уравнение на (–4) и прибавим к третьему; второе уравнение умножим на (–4) и прибавим к четвертому, получим:

![]() .
.
Тогда получаем
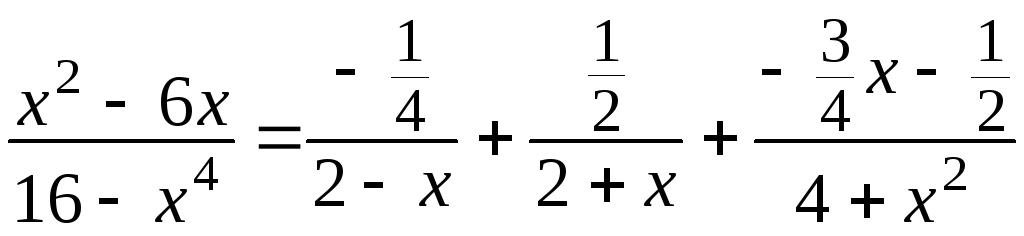 .
.
Теперь интегрируем эту сумму:
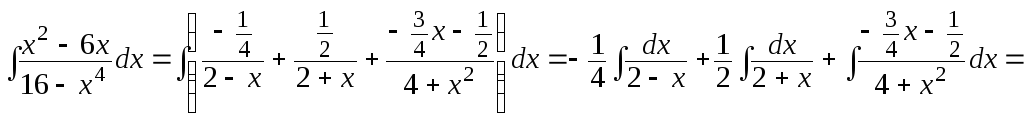
![]()
![]()
![]()
![]() .
.
в)
![]() .
Поступаем аналогично:
.
Поступаем аналогично:
![]()
![]() .
.
Тогда получим
![]() ,
,
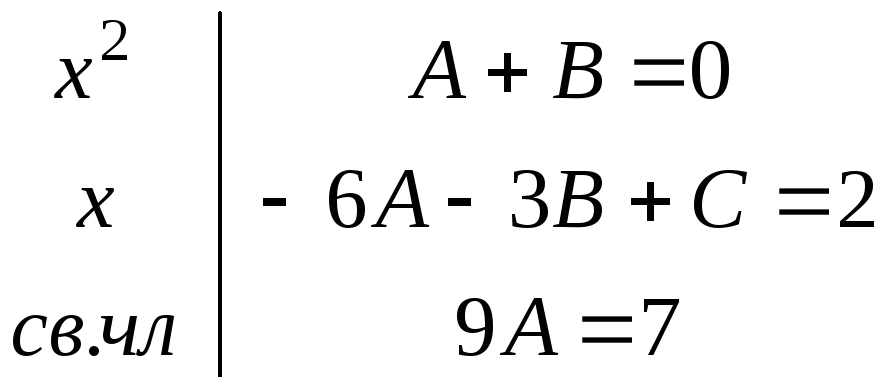
![]() .
.
Отсюда
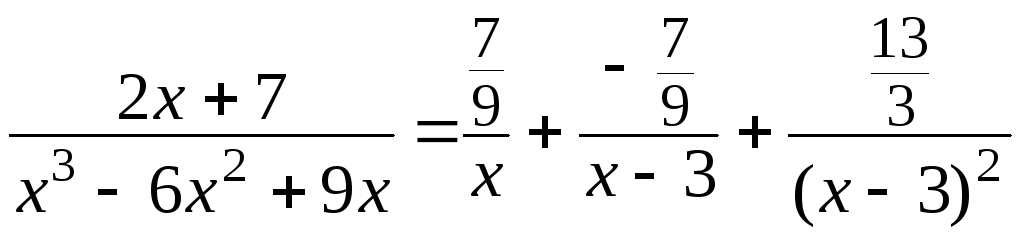 .
.
Теперь интегрируем
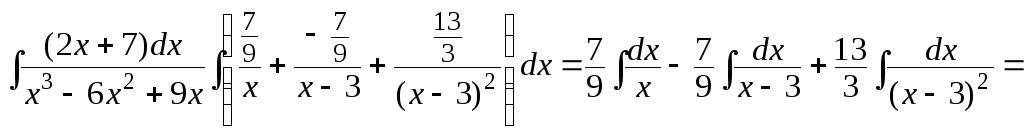
![]() .
.
Здесь
использовано свойство логарифмов:
![]() .
.
Пример 2. Найти интегралы:
а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Решение.
а)
Вычисление
![]() от правильной рациональной дроби
проводим аналогично тому, как делали
это в примере 1. Разложим дробь на
простейшие,
от правильной рациональной дроби
проводим аналогично тому, как делали
это в примере 1. Разложим дробь на
простейшие,
учитывая, что знаменатель есть разность кубов и его можно представить в виде произведения по соответствующей формуле сокращенного умножения:
![]() .
.
Приравняем числители дробей:
![]() .
.
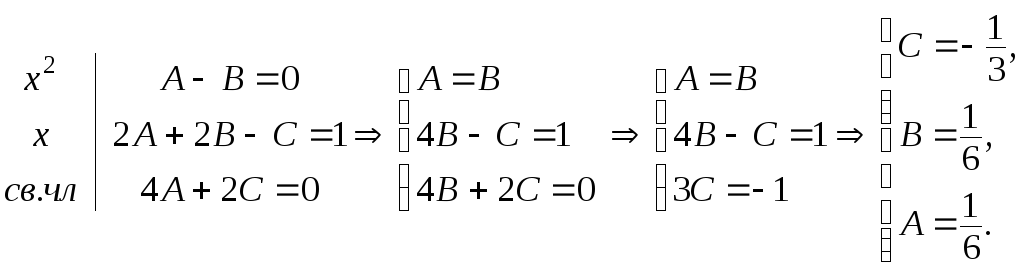
Тогда
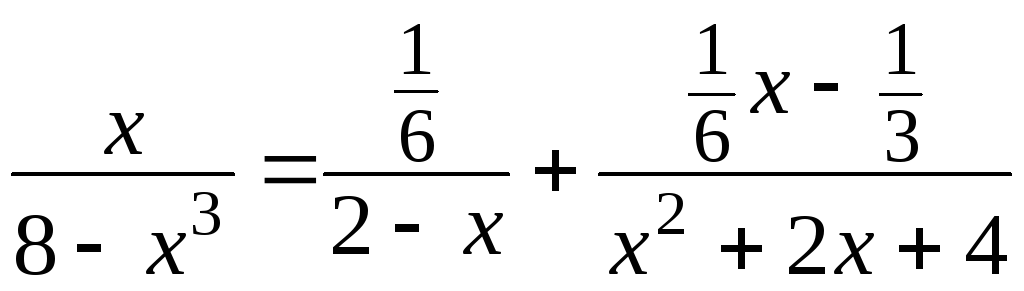 .
.
Теперь интегрируем:
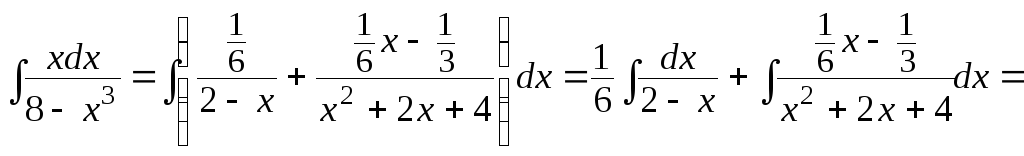
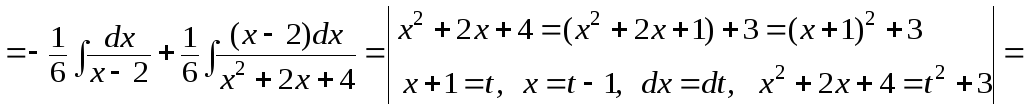
![]()
![]()
![]()
![]()
![]()
б)
Вычислим
![]() .
Подынтегральная дробь – неправильная,
поэтому сначала разделим числитель на
знаменатель:
.
Подынтегральная дробь – неправильная,
поэтому сначала разделим числитель на
знаменатель:
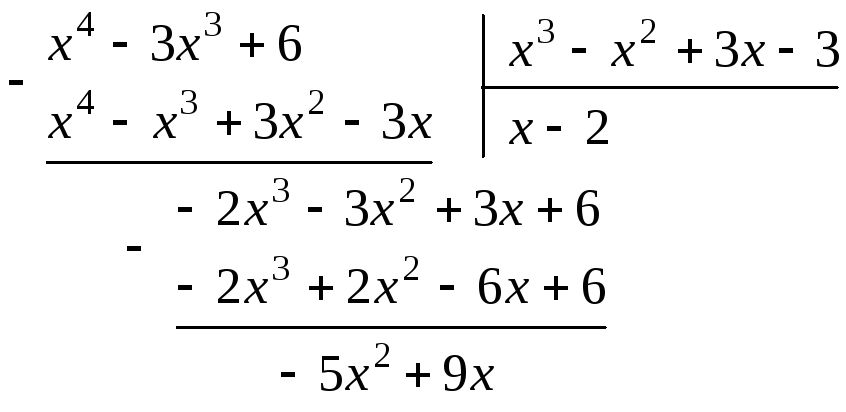
Тогда исходный интеграл можно представить в виде суммы интегралов:
![]() .
.
Первый из этих интегралов легко вычисляется:
![]() .
.
Вычислим
второй интеграл
![]() – интеграл от правильной рациональной
дроби. Для этого, прежде всего, разложим
знаменатель на неприводимые множители:
– интеграл от правильной рациональной
дроби. Для этого, прежде всего, разложим
знаменатель на неприводимые множители:
![]() .
.
Тогда
![]() .
.
Приравниваем числители первой и последней дробей:
![]() .
.
Приравнивая коэффициенты при одинаковых степенях в левой и правой частях этого равенства, получим систему уравнений относительно неизвестных коэффициентов и решим её:

Тогда разложение дроби имеет вид
![]() .
.
А интеграл от этой функции равен
![]()
![]()
![]() .
.
Теперь можно зависать окончательный результат вычислений исходного интеграла:
![]()
![]() .
.
в)
Данный интеграл
![]() – от правильной рациональной дроби,
поэтому разложим подынтегральную дробь
на простейшие дроби. Для этого сначала
разложим знаменатель на неприводимые
множители. В отличие от предыдущего
примера, группировка слагаемых к цели
не приведет. Поэтому попробуем найти
хотя бы один корень многочлена
– от правильной рациональной дроби,
поэтому разложим подынтегральную дробь
на простейшие дроби. Для этого сначала
разложим знаменатель на неприводимые
множители. В отличие от предыдущего
примера, группировка слагаемых к цели
не приведет. Поэтому попробуем найти
хотя бы один корень многочлена
![]() .
Известно из алгебры, что если многочлен
имеет целочисленные корни, то их нужно
искать среди делителей свободного
члена. Свободный член (–6) нашего
многочлена делится на числа
.
Известно из алгебры, что если многочлен
имеет целочисленные корни, то их нужно
искать среди делителей свободного
члена. Свободный член (–6) нашего
многочлена делится на числа
![]() .
Проверим подстановкой, является ли
какое-либо из этих чисел корнем многочлена:
.
Проверим подстановкой, является ли
какое-либо из этих чисел корнем многочлена:
![]() ,
,
значит,
число 1 – корень данного многочлена
![]() .
.
Разделим
многочлен
![]() на двучлен (х–1):
на двучлен (х–1):

Тогда
имеет место разложение
![]() .
.
Найдем
корни квадратного трехчлена
![]() ,
решив уравнение
,
решив уравнение
![]() =0,
получим
=0,
получим
![]() .
Значит, справедливо равенство
.
Значит, справедливо равенство![]() .
Тогда можно записать
.
Тогда можно записать
![]() .
.
Теперь можно разложить заданную дробь на простейшие:
![]()
![]() .
.
Приравниваем числители:
![]() ,
,
![]() ,
,
![]() .
.
Приравнивая коэффициенты при одинаковых степенях переменной, получим:
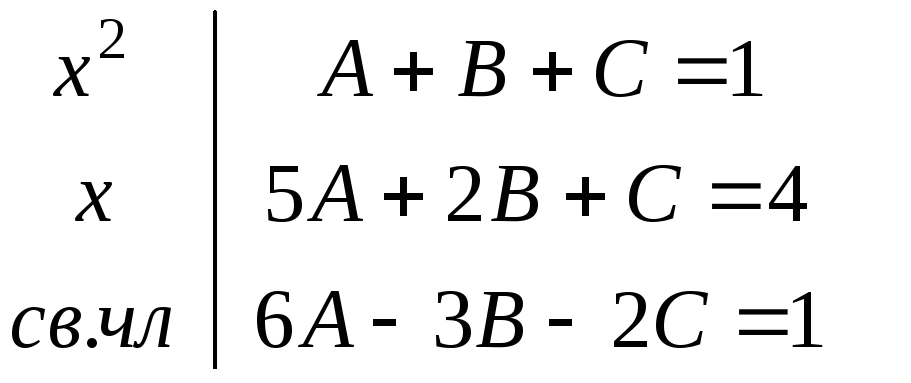
П олученную
систему уравнений решим методом Гаусса:
олученную
систему уравнений решим методом Гаусса:
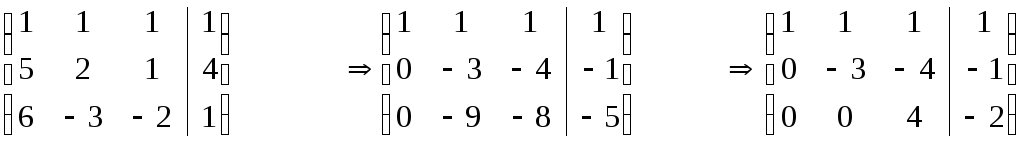
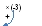
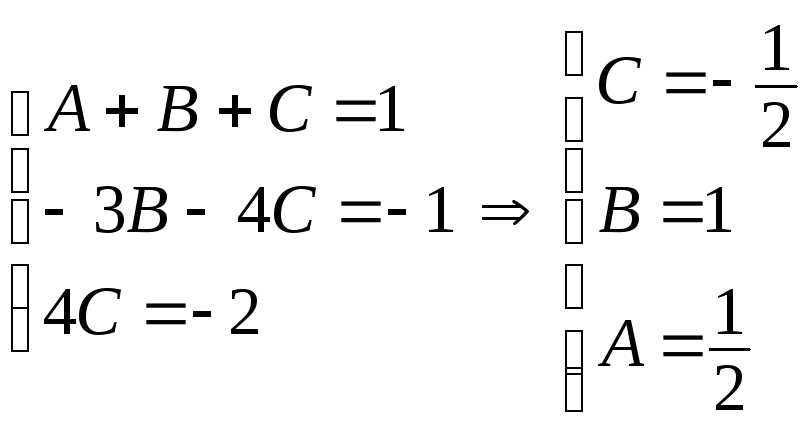
Следовательно, имеем разложение:
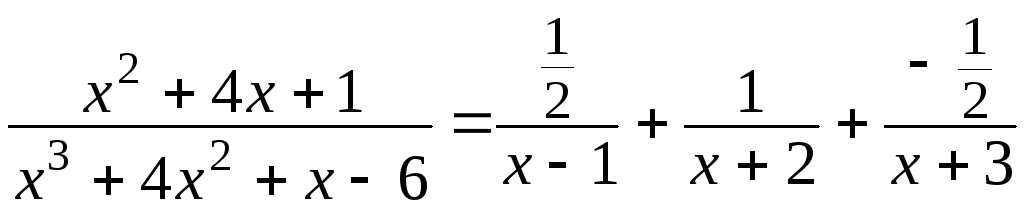 .
.
Теперь можно проинтегрировать:
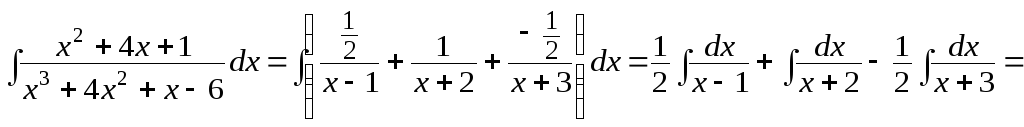
![]() .
.
Пример 3. Найти интегралы:
а)![]() ;
б)
;
б)![]() .
.
Решение.
а)
В заданном интеграле
![]() подынтегральная функция есть правильная
рациональная дробь, причем знаменатель
её уже разложен на неприводимые
множители*).
Запишем разложение на простейшие дроби:
подынтегральная функция есть правильная
рациональная дробь, причем знаменатель
её уже разложен на неприводимые
множители*).
Запишем разложение на простейшие дроби:
![]()
Приравниваем числители исходной и полученной дробей:
![]() ,
,
![]() .
.
Теперь приравняем коэффициенты при одинаковых степенях переменной в левой и правой частях последнего равенства. Получим:
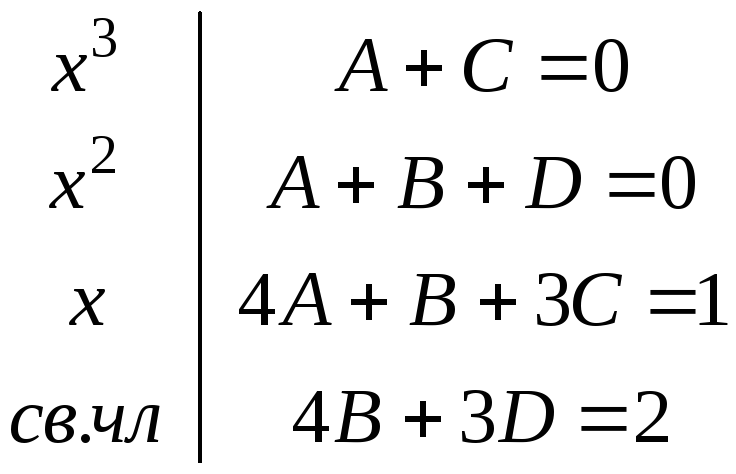
С нова
применим метод Гаусса:
нова
применим метод Гаусса:


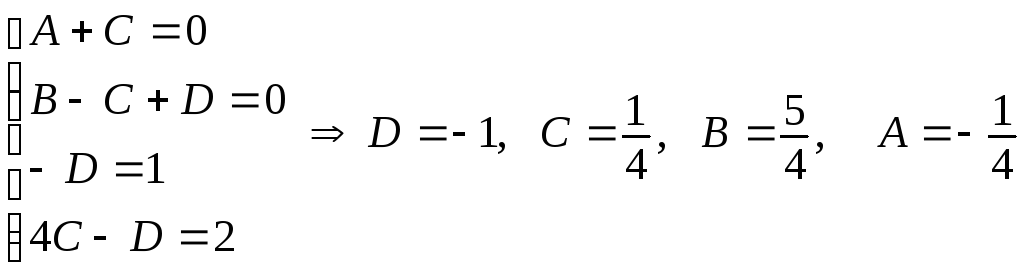 .
.
Теперь можно записать разложение подынтегральной функции
 .
.
Интегрируем заданную функцию:
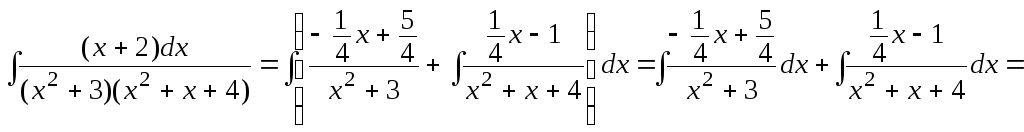
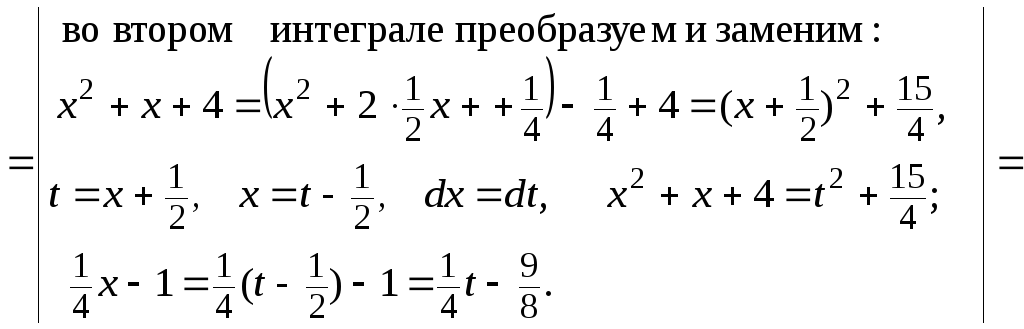
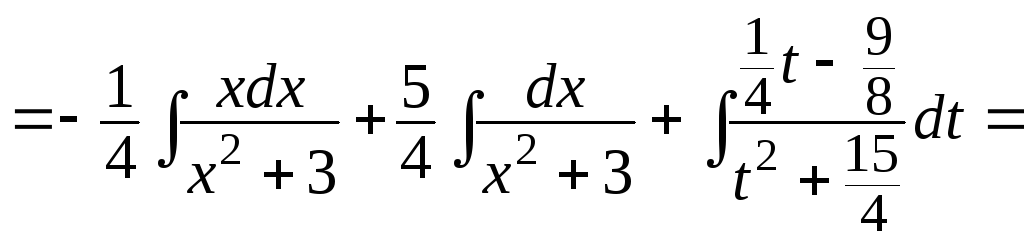
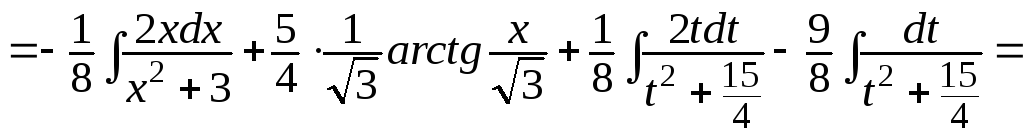

![]()
![]()
б)
В
интеграле
![]() подынтегральная функция – неправильная
рациональная дробь. Разделим числитель
этой дроби на знаменатель, чтобы выделить
целую часть:
подынтегральная функция – неправильная
рациональная дробь. Разделим числитель
этой дроби на знаменатель, чтобы выделить
целую часть:
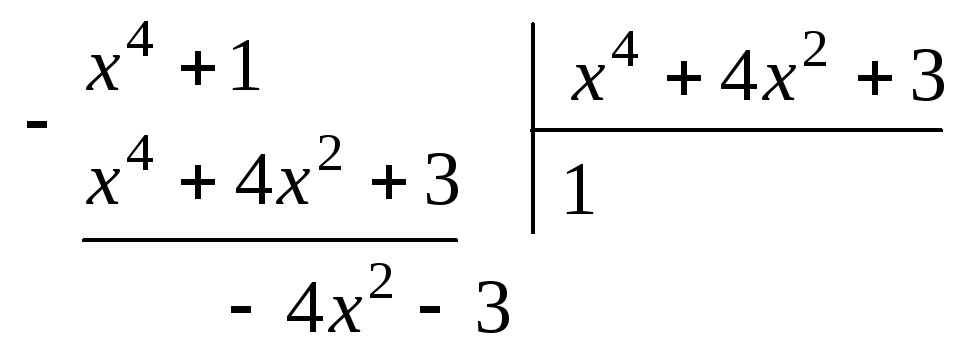
Следовательно, подынтегральная функция представима в виде суммы
![]() .
.
Рассмотрим
правильную дробь
![]() и
разложим её на простейшие дроби.
и
разложим её на простейшие дроби.
Для
этого сначала разлагаем знаменатель
на неприводимые множители. Многочлен
![]() есть биквадратный
трехчлен. Положим в нём
есть биквадратный
трехчлен. Положим в нём
![]() ,
получим
,
получим
![]() .
Этот квадратный трехчлен имеет корни
.
Этот квадратный трехчлен имеет корни
![]() ,
и, следовательно, имеет место разложение
,
и, следовательно, имеет место разложение
![]() .
Сделав в этом равенстве обратную замену
.
Сделав в этом равенстве обратную замену![]() ,
получим разложение знаменателя на
неприводимые множители:
,
получим разложение знаменателя на
неприводимые множители:
![]() .
.
Тогда можно записать
![]() .
.
Далее имеем
![]()
![]() .
.
Отсюда получим систему уравнений:
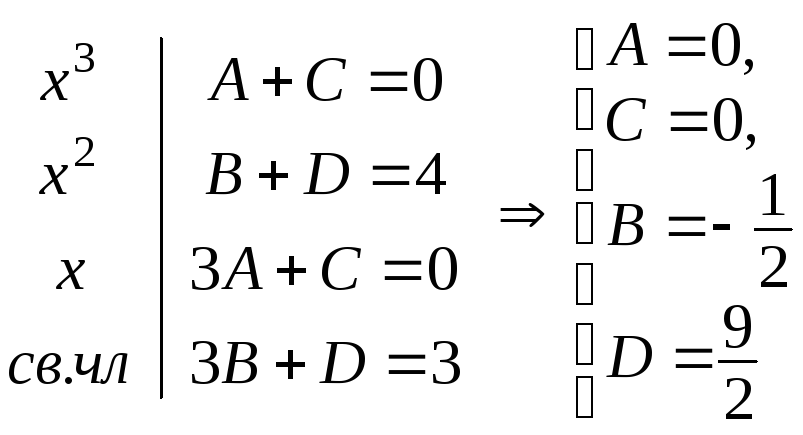
Тогда рассматриваемая дробь примет вид
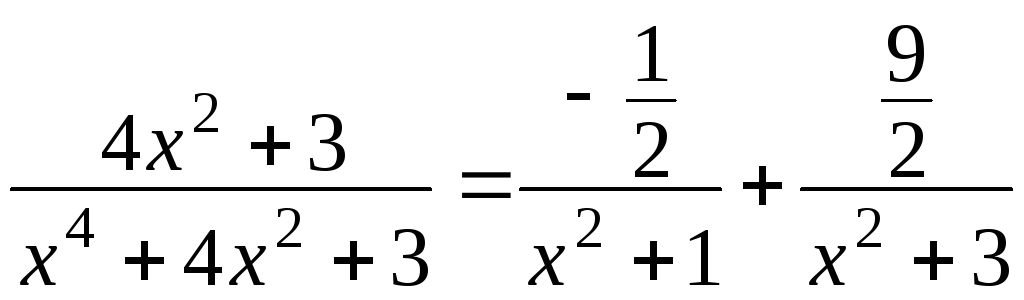
а подынтегральная функция запишется так
![]() ,
,
Теперь проинтегрируем
![]()
![]() .
.
*)
Квадратный
трехчлен
![]() не
имеет действительных корней, т.к. у него
отрицательный дискриминант:
не
имеет действительных корней, т.к. у него
отрицательный дискриминант:![]() .
.
