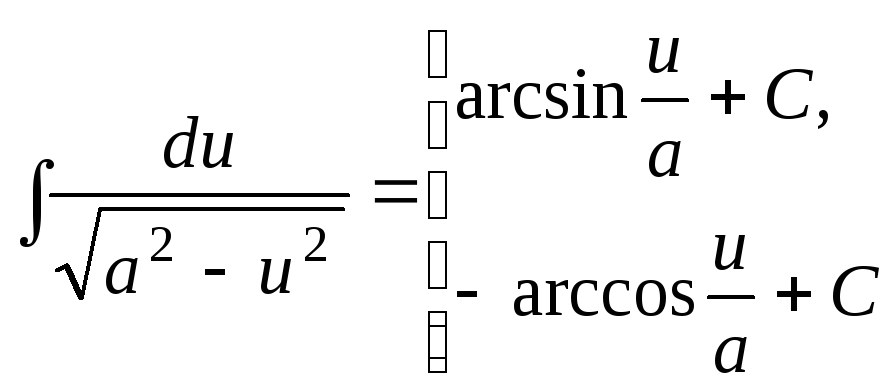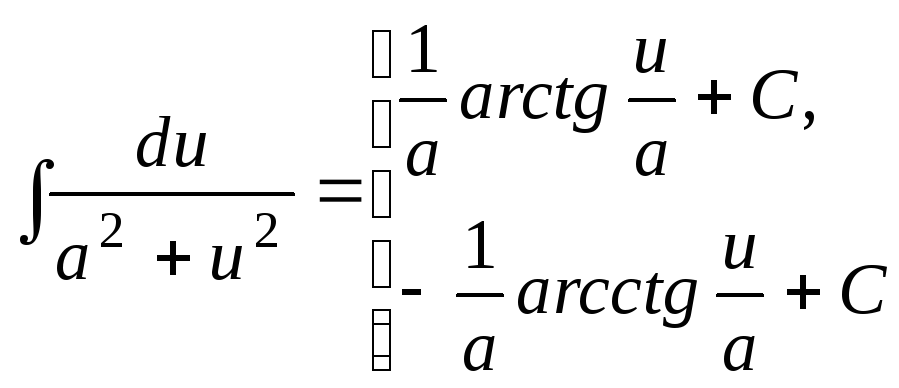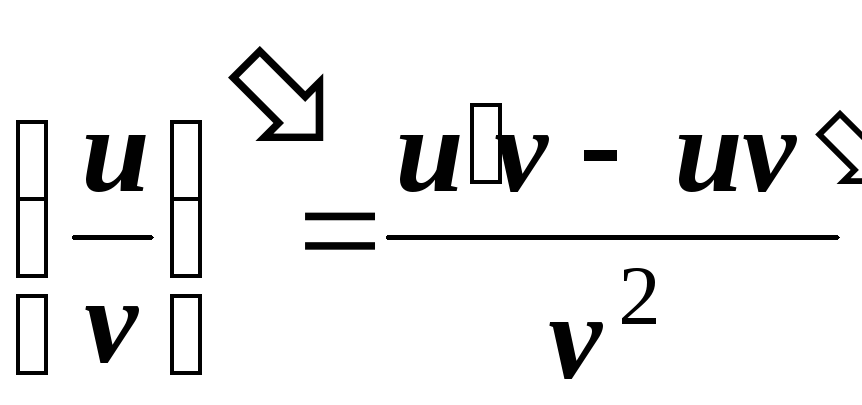FAIT1 / Интегралы-Помощь / 1. Непосредственное интегрирование
.doc-
Неопределенный интеграл
Поскольку сейчас речь пойдет только о неопределенном интеграле, то для сокращения термин «неопределенный» будем опускать.
Для того чтобы научиться вычислять интегралы (или, как говорят, интегрировать функции), нужно, прежде всего, выучить таблицу интегралов:
Таблица1. Таблица интегралов
|
1.
2.
2a.
2б.
2в.
3.
3а.
4.
5.
5а)
6.
6а.
7.
7а.
|
8.
9.
10.
10а.
11.
11а.
12.
13.
13а.
|
Кроме того, потребуется умение вычислять производную от заданной функции, а значит, нужно вспомнить правила дифференцирования и таблицу производных основных элементарных функций:
Таблица 2. Таблица производных и правила дифференцирования:
6.а.
|
(sin и) = cos и и (cos u) = – sin и и |
|
А еще нам потребуется
умение находить дифференциал функции.
Напомним, что дифференциал функции
![]() находят по формуле
находят по формуле
![]() ,
т.е. дифференциал функции равен
произведению производной этой функции
на дифференциал её аргумента. Полезно
держать в памяти и следующие известные
соотношения:
,
т.е. дифференциал функции равен
произведению производной этой функции
на дифференциал её аргумента. Полезно
держать в памяти и следующие известные
соотношения:
Таблица 3. Таблица дифференциалов
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
|
10.
11.
12.
13.
14.
15.
16.
17.
|
Причем использовать эти формулы можно, как читая их слева направо, так и справа налево.
Рассмотрим последовательно три основных приема вычисления интеграла. Первый из них называют методом непосредственного интегрирования. Он основан на использовании свойств неопределенного интеграла, включает два основных приема: разложение интеграла на алгебраическую сумму более простых и подведение под знак дифференциала, причем эти приемы могут быть использованы как самостоятельно, так и в совокупности.
А)
Рассмотрим
разложение на алгебраическую сумму
– этот прием предполагает использование
тождественных преобразований
подынтегральной функции и свойств
линейности неопределенного интеграла:
![]() и
и
![]() .
.
Пример 1. Найти интегралы:
а) ;
б)
;
б)
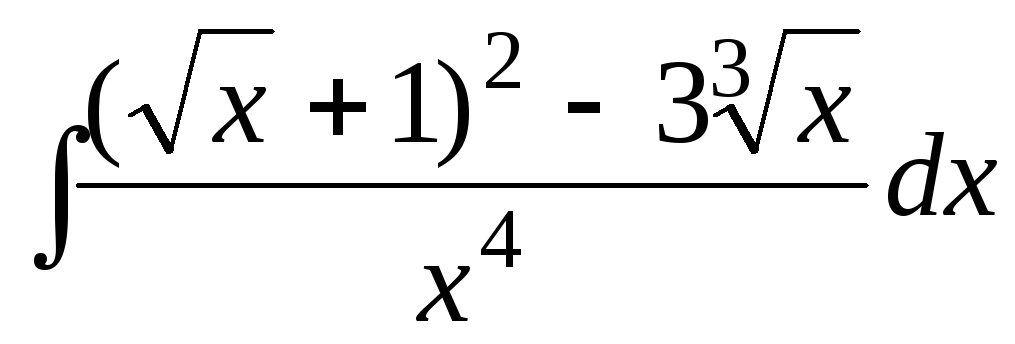 ;
;
в)
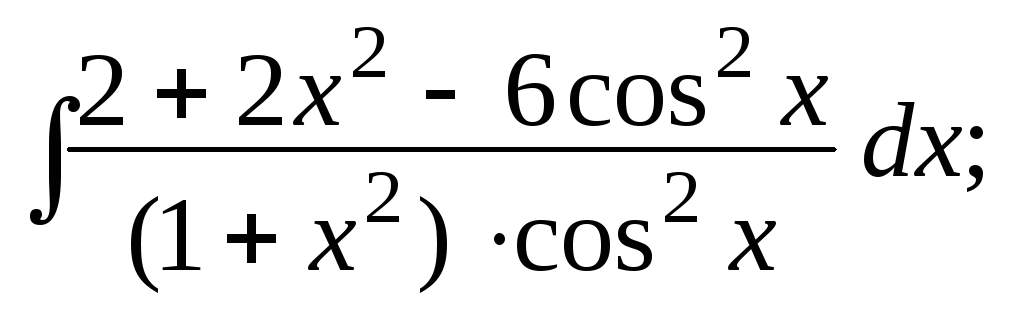 г)
г)
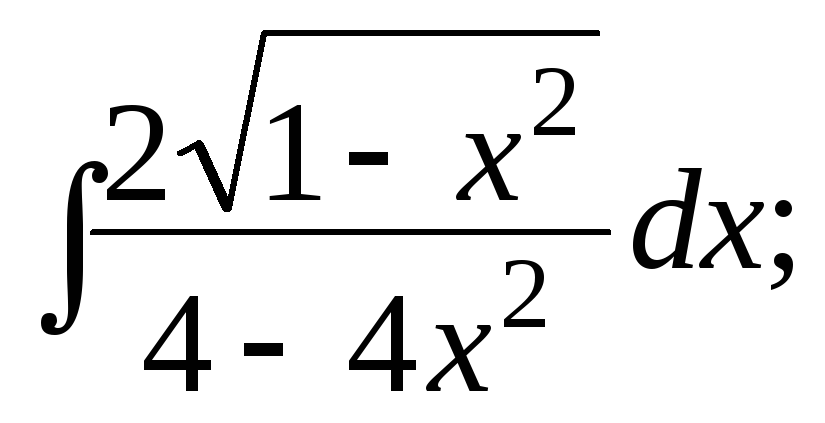
д)
![]() .
.
Решение.
а) Преобразуем подынтегральную функцию, разделив почленно числитель на знаменатель:
![]()

![]() .
.
Здесь использовано
свойство степеней:
![]() .
.
б) Сначала преобразуем числитель дроби, затем разделим почленно числитель на знаменатель:
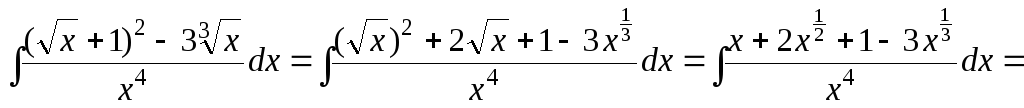

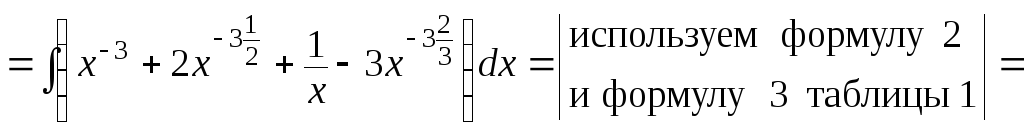
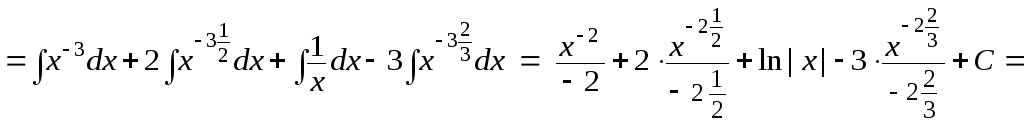
 .
.
Здесь также
использовано свойство степеней:
![]() .
.
в)
![]()
![]()
![]()
 .
.
![]()
г)
![]()
 .
.
Здесь использовано
свойство:
![]() ,
,
![]() .
.
д)
![]()
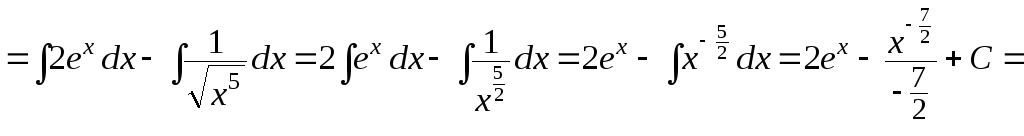
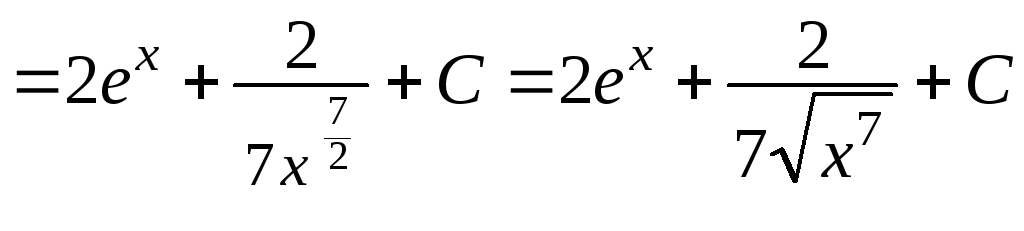 .
.
Здесь использованы формулы 2 и 5 таблицы 1.
Пример 2. Найти интегралы:
а)
 ;
б)
;
б)
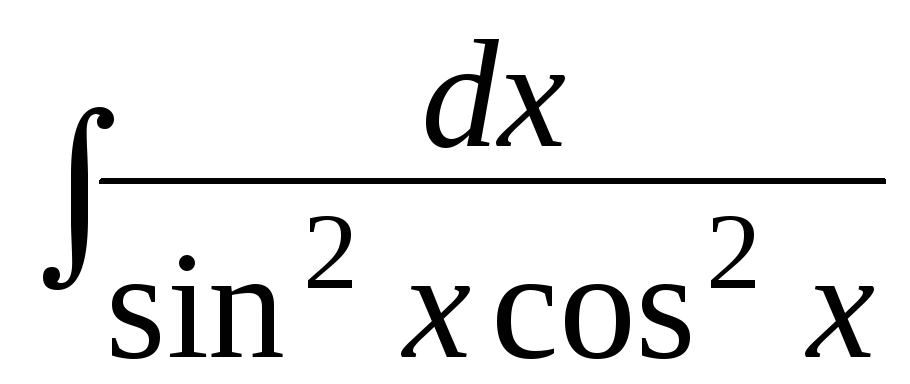 ;
;
в)
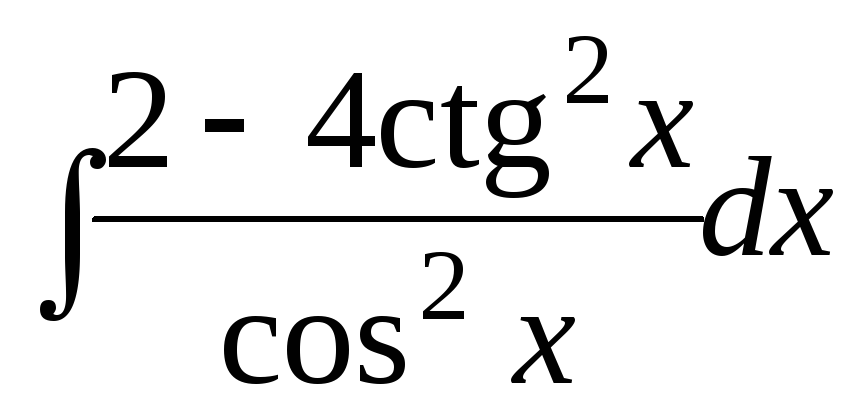 г)
г)
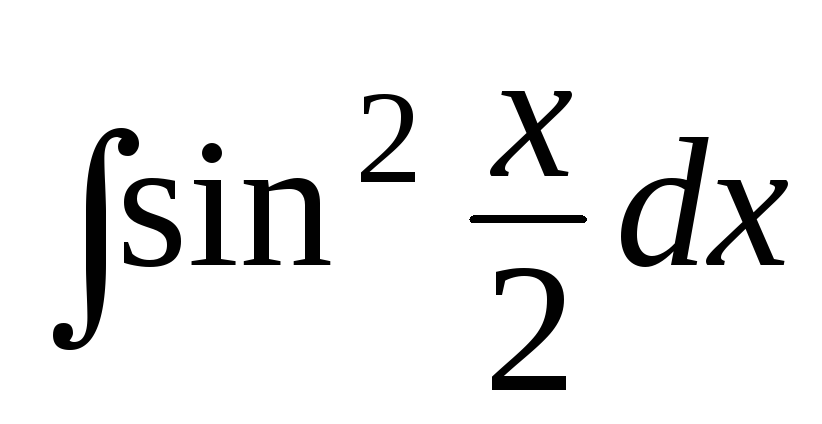
д)
![]() .
.
Решение.
а)
Преобразуем
подынтегральную функцию, используя
тригонометрическое тождество
![]() :
:
![]()
![]() .
.
Здесь вновь использовано почленное деление числителя на знаменатель и формулы 8 и 9 таблицы 1.
б)
Аналогично
преобразуем, используя тождество
![]() :
:
![]()
![]()
![]() .
.
в)
Сначала
разделим почленно числитель на знаменатель
и вынесем за знак интеграла константы,
затем используем тригонометрическое
тождество
![]() :
:
![]()
 .
.
г) Применим формулу понижения степени:
![]() ,
,
Получим:
![]() .
.
д) Используя тригонометрические тождества, преобразуем:
![]() .
.
![]() .
.
Б) Рассмотрим прием интегрирования, который называют подведением под знак дифференциала. В основе этого приема лежит свойство инвариантности неопределенного интеграла:
если
![]() ,
то для любой дифференцируемой функции
и = и(х) имеет место:
,
то для любой дифференцируемой функции
и = и(х) имеет место:
![]() .
.
Это свойство позволяет значительно расширить таблицу простейших интегралов, так как в силу этого свойства формулы таблицы 1 справедливы не только для независимой переменной и, но и в случае, когда и – дифференцируемая функция какой-либо другой переменной.
Например,
![]() ,
но и
,
но и
![]() ,
и
,
и
![]() ,
и
,
и
![]() .
.
Или
![]() и
и
![]() ,
и
,
и
![]() .
.
Суть метода заключается в выделении в заданном подынтегральном выражении дифференциала некоторой функции так, чтобы этот выделенный дифференциал вместе с остальным выражением составляли табличную формула относительно этой функции. В случае необходимости при таком преобразовании можно соответствующим образом добавлять константы. Например:
а)
 ;
;
б)
![]()
![]() .
.
в)
![]()
(в последнем примере записано ln(3 + x2) вместо ln|3 + x2| , так как выражение 3 + x2 всегда положительно).
Пример
3.
Найти
интегралы:
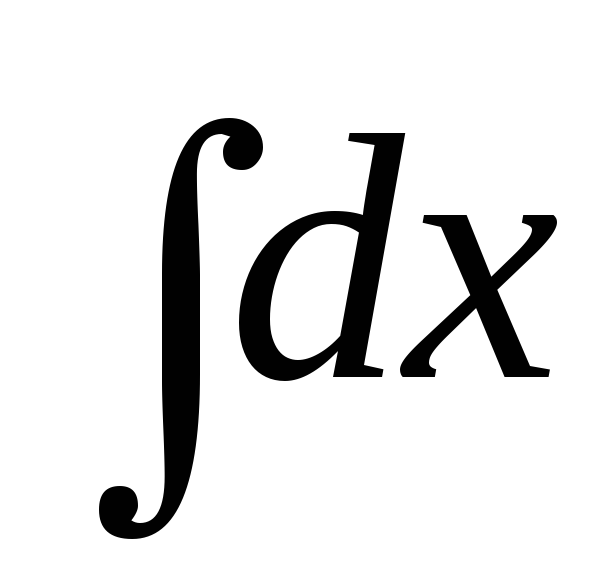
а)
 ;
б)
;
б)
 ;
в)
;
в)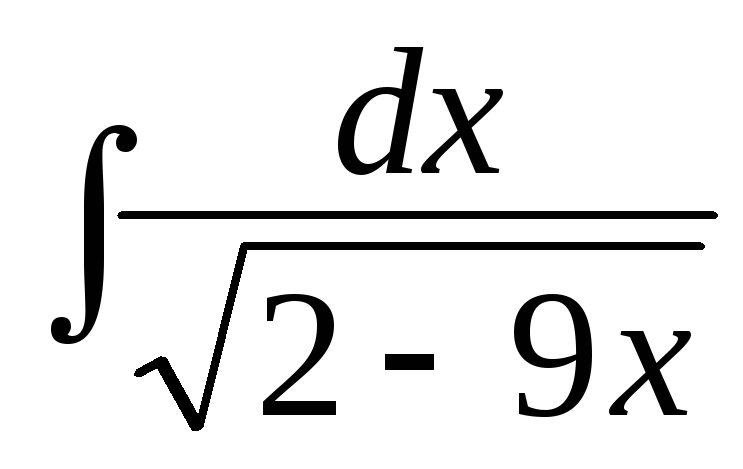 ;
;
г)
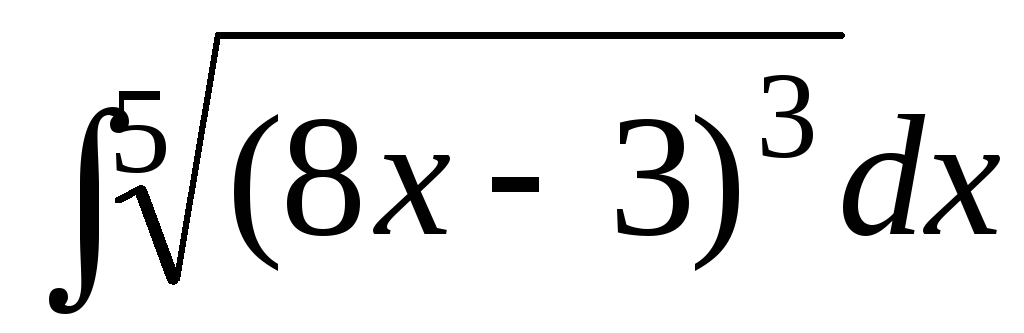 ;
д)
;
д)
 ;
е)
;
е)
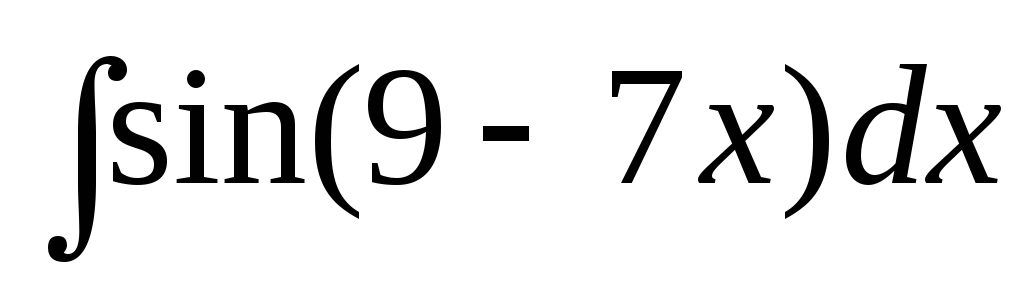 ;
;
ж)
 ;
з)
;
з)
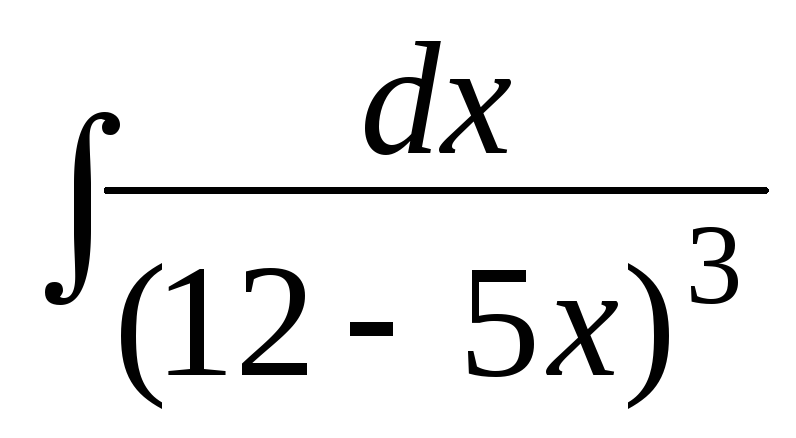 .
.
Решение.
а)
![]() .
.
Здесь использованы формулы 2а, 5а и 7а таблицы 1, две последние из которых получены как раз путем подведения под знак дифференциала:
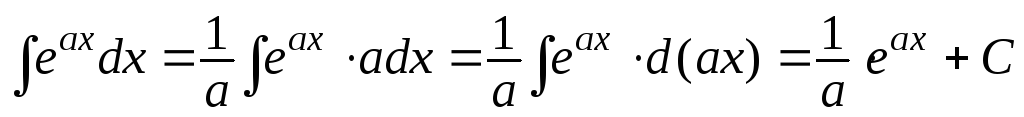 ,
,
![]() .
.
Интегрировать
функции вида
![]() приходится очень часто в рамках вычисления
интегралов от более сложных функция.
Чтобы каждый раз не повторять описанные
выше действия, рекомендуем запомнить
соответствующие формулы, приведённые
в таблице 1.
приходится очень часто в рамках вычисления
интегралов от более сложных функция.
Чтобы каждый раз не повторять описанные
выше действия, рекомендуем запомнить
соответствующие формулы, приведённые
в таблице 1.
б)
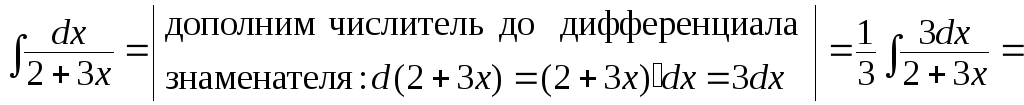
![]() .
.
Здесь использована формула 3 таблицы 1.
в)
Аналогично,
учитывая что
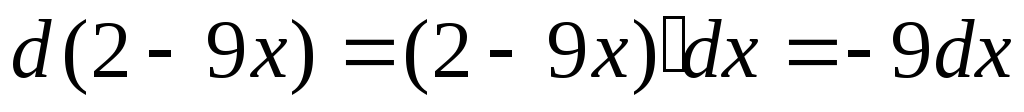 ,
преобразуем:
,
преобразуем:
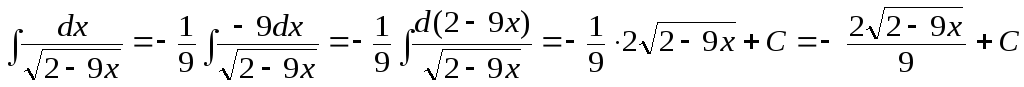 .
.
Здесь использована формула 2в таблицы 1.
г)

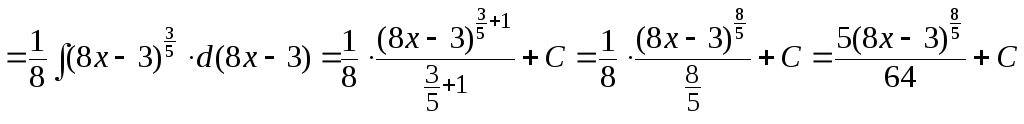 .
.
д)
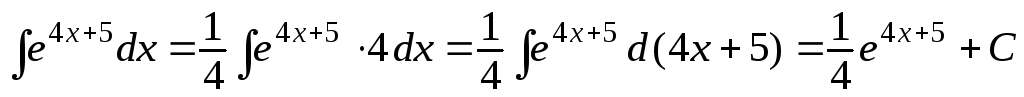 ;
;
е)

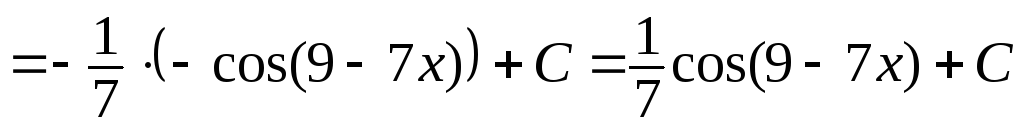 .
.
ж)
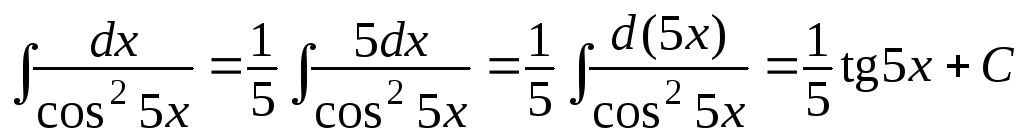 ;
;
з)
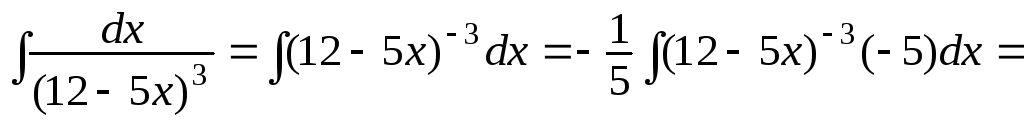
![]()
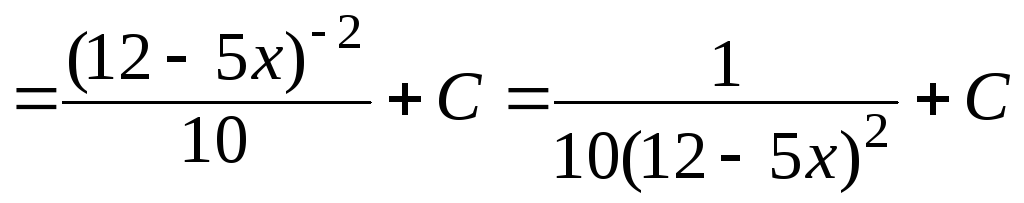 .
.
Пример 4. Найти интегралы:
а)
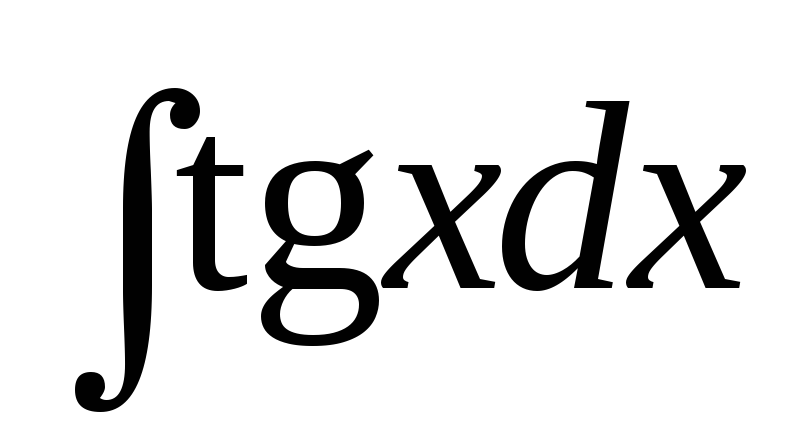 б)
б)
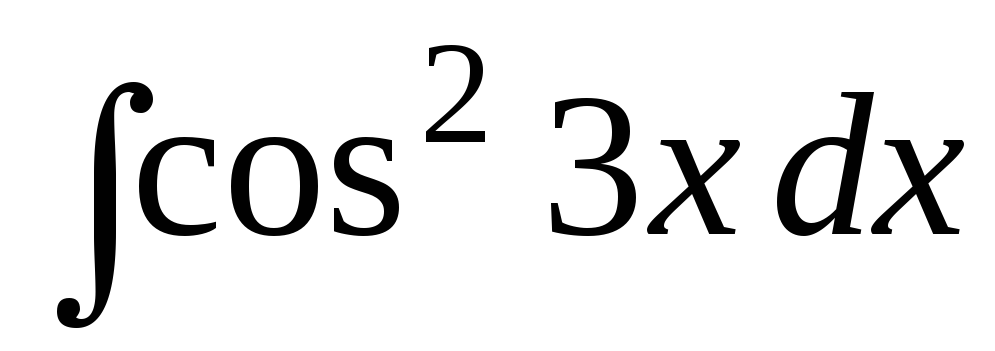
в)
![]() .
.
Решение.
а) Преобразуем:
![]() .
.
Здесь так же использована формула 3 таблицы 1.
б)
Используем формулу понижения степени
![]() :
:
![]()
![]() .
.
Здесь использованы формулы 2а и 7а таблицы 1.
в)
![]()
![]()
![]() .
.
Здесь наряду с
формулами 2 и 8 таблицы 1 использованы и
формулы таблицы 3:
![]() ,
,
![]() .
.
Пример 5. Найти интегралы:
а)
![]() ;
б)
;
б)
![]()
в)![]() ;
г)
;
г)
![]() .
.
Решение.
а)
Произведение
![]() можно дополнить (см. формулы 4 и 5 таблицы
3) до
дифференциала функции
можно дополнить (см. формулы 4 и 5 таблицы
3) до
дифференциала функции
![]() ,
где а
и b
– любые константы,
,
где а
и b
– любые константы,
![]() .
Действительно,
.
Действительно,
![]() ,
откуда
,
откуда
![]() .
.
Тогда имеем:


![]() .
.
б)
Используя формулу 6 таблицы 3, имеем
![]() ,
а также
,
а также
![]() ,
значит, присутствие в подынтегральном
выражении произведения
,
значит, присутствие в подынтегральном
выражении произведения
![]() означает подсказку: под знак дифференциала
нужно внести выражение
означает подсказку: под знак дифференциала
нужно внести выражение
![]() .
Поэтому получаем
.
Поэтому получаем
![]() .
.
в) Так
же как в пункте б), произведение
![]() можно дополнить до дифференциала
функции
можно дополнить до дифференциала
функции
![]() .
Тогда получим:
.
Тогда получим:
![]()
![]() .
.
г) Сначала воспользуемся свойствами линейности интеграла:
![]()
![]()
![]() .
.
Пример 6. Найти интегралы:
а)
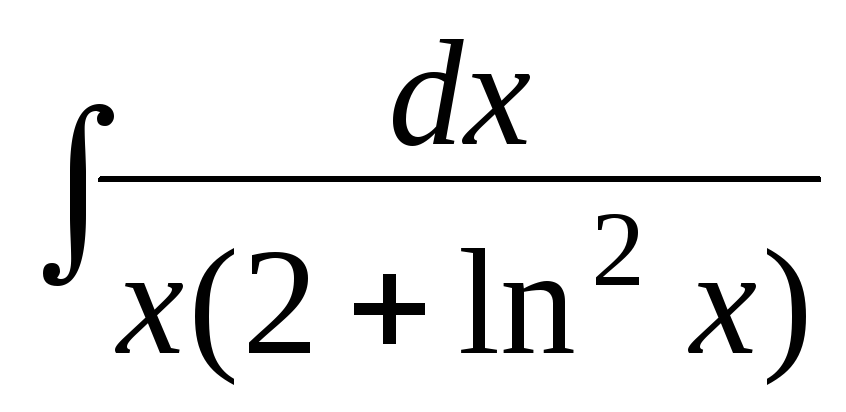 ;
б)
;
б)
 ;
;
в) 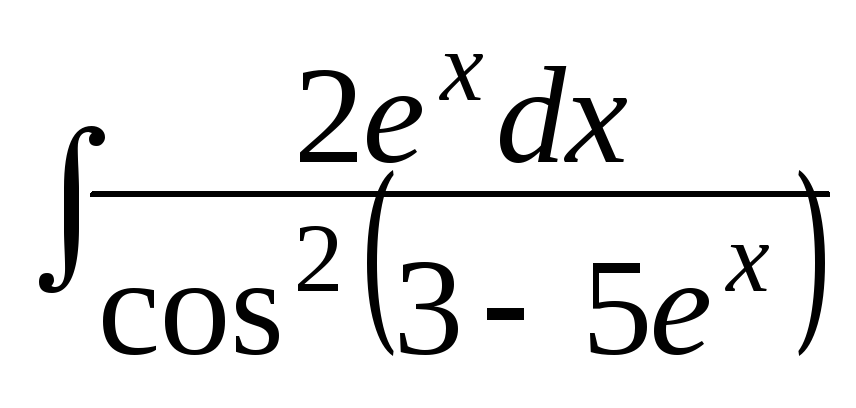 ; г)
; г)
 .
.
Решение.
а)
Учитывая,
что
![]() (формула 9 таблицы 3), преобразуем:
(формула 9 таблицы 3), преобразуем:
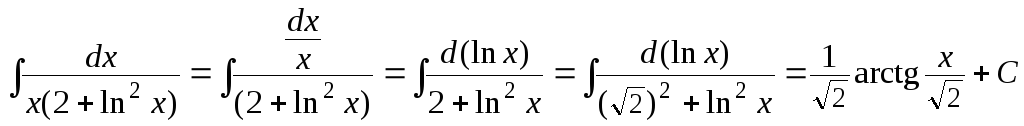 .
.
б) Используя формулу 12 таблицы 3, получим
![]()
в) Учитывая формулу 11 таблицы 3, преобразуем
![]()
г) Используя формулу 16 таблицы 3, получим:
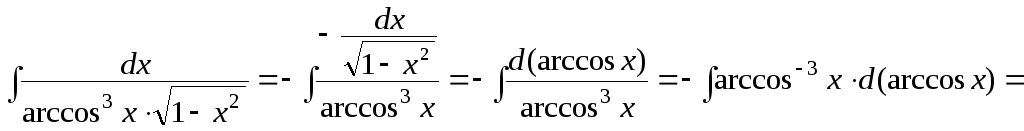
![]() .
.
Пример 7. Найти интегралы:
а)
 ;
б)
;
б)
 ;
;
в)
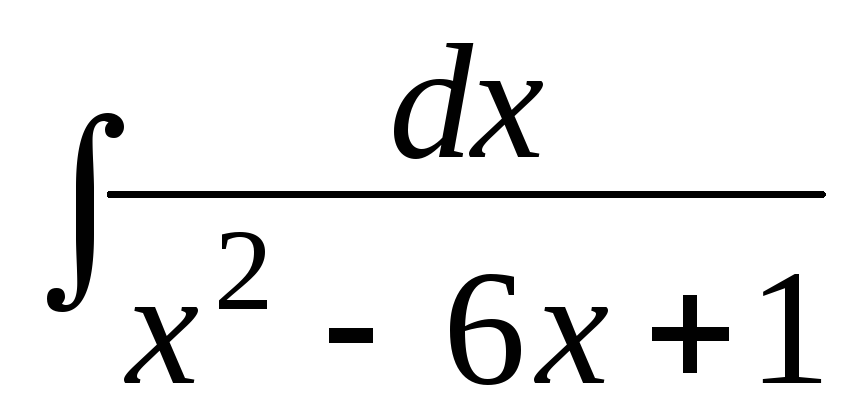 ; г)
; г)
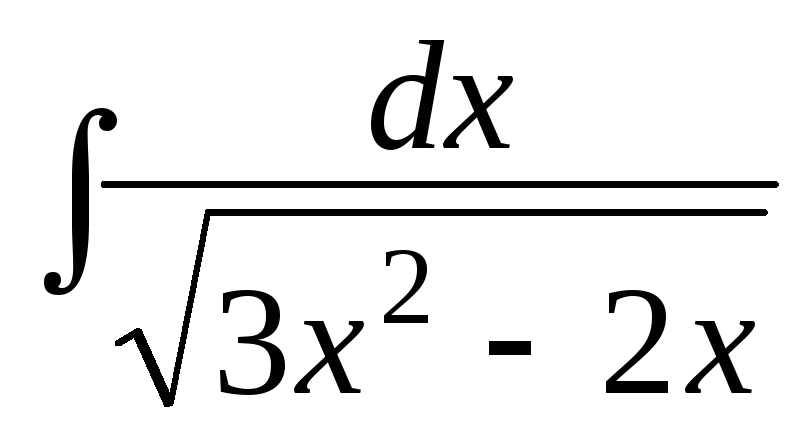 .
.
Решение.
а) Все представленные в этом примере интегралы имеют общую особенность: подынтегральная функция содержит квадратный трехчлен. Поэтому и способ вычисления этих интегралов будет основан на одном и том же преобразовании – выделении полного квадрата в этом квадратном трехчлене.
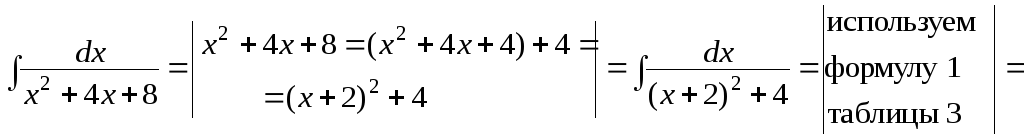
![]() .
.
б)
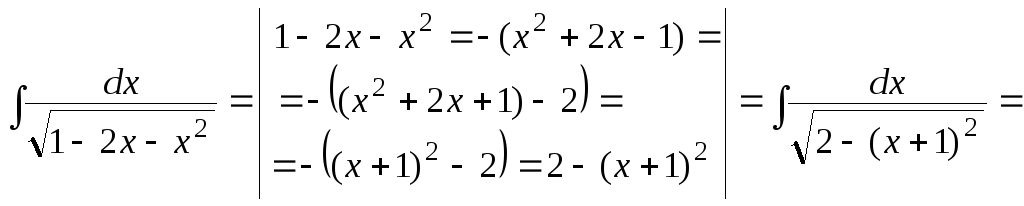
 .
.
в)
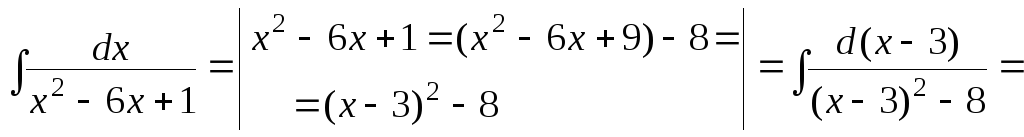
 .
.
г)
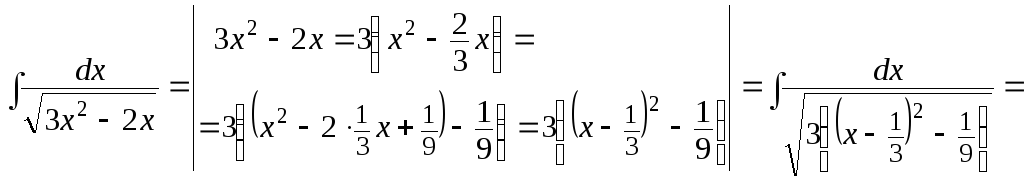

![]() .
.
Прием подведения под знак дифференциала является устной реализацией более общего приема вычисления интеграла, называемого методом подстановки или заменой переменной. Действительно, каждый раз, подбирая подходящую формулу таблицы 1 к полученной в результате подведения под знак дифференциала функции, мы мысленно заменяли буквой и функцию, внесенную под знак дифференциала. Поэтому, если интегрирование путем подведения под знак дифференциала не очень получается, можно непосредственно делать замену переменной. Подробнее об этом – в следующем пункте.