FAIT1 / Интегралы-Помощь / 3. Замена переменной (метод подстановки)

2. Замена переменной (метод подстановки)

Суть метода подстановки заключается в том, что в результате введения новой переменной заданный сложный интеграл приводится к табличному или такому, прием вычисления которого известен.

Пусть требуется вычислить интеграл . Существует два правила подстановки:

1. Независимую переменную заменяют по формуле , где -дифференцируемая функция, имеющая обратную . Затем обязательно находят , преобразовывают заданный интеграл и вычисляют полученный:

.

Общего правила подбора функции не существует, но есть несколько типов подынтегральных функций, для которых имеются рекомендации по подбору функции.

2. Полагают , затем либо находят и с его помощью заменяют часть подынтегрального выражения, либо выражают х, по нему находят dx и подставляют в подынтегральное выражение. В результате получается интеграл относительно переменной t, вычисление которого осуществить проще, чем исходного. Часто функцию выбирают либо интуитивно из желания убрать какое-либо сложное выражение, либо из тех соображений, что в подынтегральном выражении можно выделить дифференциал некоторой функции .

Замену переменных можно применять несколько раз, пока не будет получен результат.

Пример 1. Найти интегралы:

а) ; б) ; в) ;

г) ; д) ; е).

Решение.

а) Среди табличных интегралов нет содержащих радикалы различных степеней, поэтому «хочется избавиться», прежде всего, от и . Для этого потребуется заменить х таким выражением, из которого легко извлекались бы оба корня:

;

б) Типичный пример, когда возникает желание «избавиться» от показательной функции . Но в данном случае удобнее за новую переменную взять всё выражение, стоящее в знаменателе дроби:

;

в) Замечая, что в числителе стоит произведение , являющееся частью дифференциала подкоренного выражения, заменим все это выражение новой переменной:

;

г) Здесь, как и в случае а), хочется избавиться от радикала. Но поскольку, в отличие от пункта а), здесь только один корень, то именно его и заменим новой переменной:

.

д) Здесь выбору замены способствуют два обстоятельства: с одной стороны интуитивное желание избавиться от логарифмов, с другой стороны – наличие выражения , являющегося дифференциалом функции . Но так же как и в предыдущих примерах, в замену лучше включить и сопутствующие логарифму константы:

.

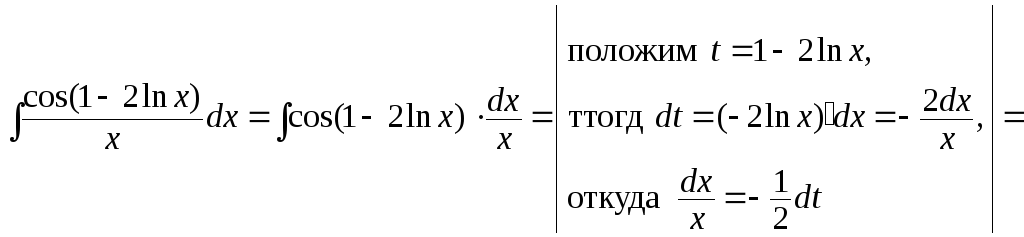
е) Здесь, так же как и в предыдущем примере, интуитивное желание избавиться от громоздкого показателя в подынтегральной функции согласуется с известным фактом: (формула 8 таблицы 3). Поэтому имеем:

.

Замена переменных для некоторых классов функций

Рассмотрим некоторые классы функций, для которых могут быть рекомендованы определенные подстановки.

Таблица 4. Рациональные функции

Вид интеграла	Способ интегрирования
1.1.
1.2.
1.3.	Выделение полного квадрата:
1.4.	Рекуррентная формула

Трансцендентные функции:

1.5. – подстановка t = e^x;

1.6. – подстановка t = log_ax.

Пример 2. Найти интегралы от рациональных функций:

а) ; б) ;

в) ; д) .

Решение.

а) Этот интеграл нет необходимости вычислять с помощью замены переменных, здесь проще использовать подведение под знак дифференциала:

;

б) Аналогично, используем подведение под знак дифференциала:

;

в) Перед нами интеграл типа 1.3 таблицы 4, воспользуемся соответствующими рекомендациями:

.

д) Аналогично предыдущему примеру:

.

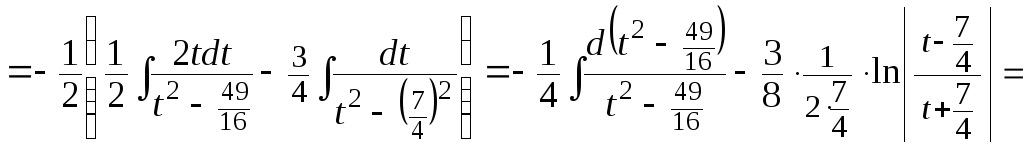
Пример 3. Найти интегралы

а) ; б) .

Решение.

а) Воспользуемся рекомендацией 1.5: если подынтегральное выражение содержит показательную функцию, то желательно заменить именно эту функцию новой переменной. Получим:

.

б) Подынтегральное выражение содержит логарифм, поэтому воспользуемся рекомендацией 1.6. Только в данном случае удобнее заменить не просто функцию , а все подкоренное выражение:

.

Таблица 6. Тригонометрические функции (R – рациональная функция своих аргументов)

Вид интеграла	Способ интегрирования
3.1.	Универсальная подстановка , , ,
3.1.1. , если	Подстановка
3.1.2. , если	Подстановка .
3.1.3. . , если (т.е. есть только четные степени функций )	Подстановка
3.2.	Если – нечетное, то см. 3.1.1; если – нечетное, то см. 3.1.2; если – четное, то см. 3.1.3; если – четные, то использовать формулы понижения степени ,
3.3. , ,	Использовать формулы , , .

Пример 4. Найти интегралы:

а) ; б) ; в) ; д) .

Решение.

а) Здесь интегрируем тригонометрическую функцию. Применим универсальную подстановку (таблица 6, 3.1):

.

б) Здесь также применим универсальную подстановку:

.

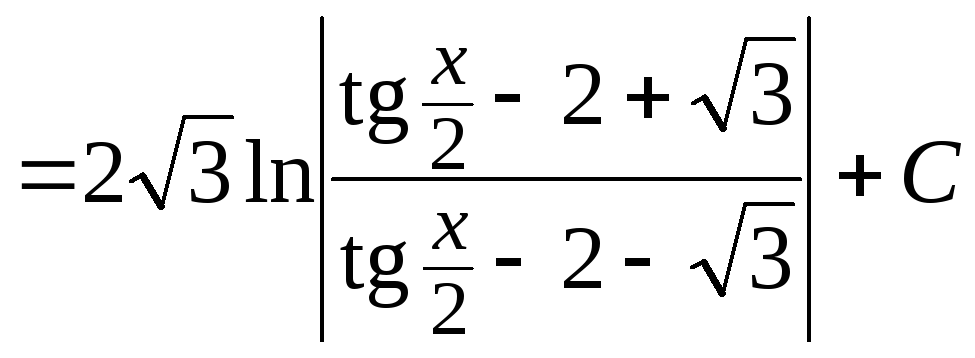Заметим, что в рассмотренном интеграле замену переменных пришлось применить дважды.

в) Вычисляем аналогично:

.

д) Рассмотрим два приема вычисления данного интеграла.

1)

.

2)

.

Как видим, получили разные функции-первообразные. Это не означает, что один из использованных приемов дает неверный результат. Дело в том, что используя известные тригонометрические тождества, связывающие тангенс половинного угла с тригонометрическими функциями полного угла, имеем

,

Таким образом, найденные первообразные совпадают друг с другом.

Пример 5. Найти интегралы:

а) ; б) ; в) ; г).

Решение.

а) В этом интеграле тоже можно применить универсальную подстановку , но поскольку входящий в подынтегральную функцию косинус – в четной степени, то рациональнее использовать рекомендации пункта 3.1.3 таблицы 6:

.

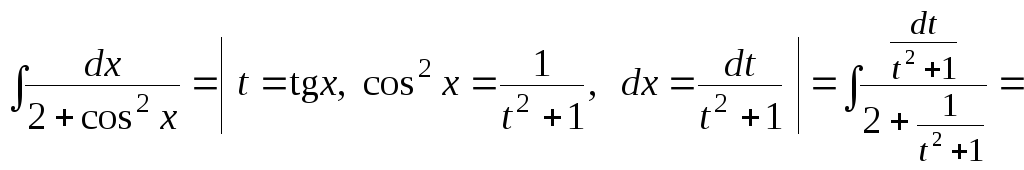
б) Сначала приведем все тригонометрические функции, входящие в подынтегральное выражение к одному аргументу:

.

В полученном интеграле можно применить универсальную подстановку, но замечаем, что подынтегральная функция не меняет знак при изменении знаков синуса и косинуса:

.

Следовательно, функция обладает свойствами, указанными в пункте 3.1.3 таблицы 6, поэтому наиболее удобной будет подстановка . Имеем:

.

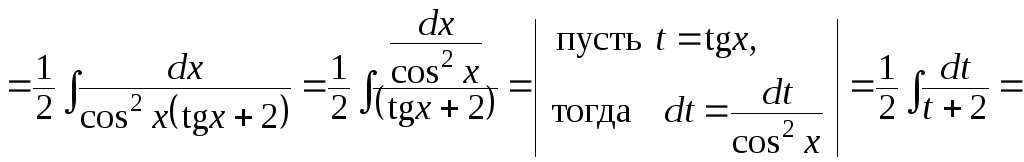
в) Если в заданной подынтегральной функции поменять знак у косинуса, то вся функция поменяет знак:

.

Значит, подынтегральная функция обладает свойством, описанным в пункте 3.1.2. Следовательно, рационально воспользоваться подстановкой . Но прежде, как и в предыдущем примере, преобразуем подынтегральную функцию:

.

г) Если в заданной подынтегральной функции поменять знак у синуса, то вся функция поменяет знак, значит, имеем случай, описанный в пункте 3.1.1 таблицы 6, поэтому новой переменной нужно обозначить функцию . Но поскольку в подынтегральном выражении не наблюдается ни наличия функции , ни ее дифференциала, предварительно преобразуем:

.

Пример 6. Найти интегралы:

а); б) ;

в) г) .

Решение.

а) Данный интеграл относится к интегралам вида 3.2 таблицы 6. Поскольку синус в нечетной степени, то согласно рекомендациям, удобно заменить функцию . Но сначала преобразуем подынтегральную функцию:

.

б) Данный интеграл относится к тому же типу, что и предыдущий, но здесь функции и имеют четные степени, поэтому нужно применить формулы понижения степени: , . Получим:

=

.

в) Преобразуем функцию:

г) Согласно рекомендациям 3.1.3 таблицы 6, в данном интеграле удобно сделать замену . Получим:

.

Таблица 5. Иррациональные функции (R – рациональная функция своих аргументов)

Вид интеграла	Способ интегрирования
2.1.	Подстановка , где k – общий знаменатель дробей …, .
2.2.	Подстановка , где k –общий знаменатель дробей …,
2.3.	Подстановка, , где k – общий знаменатель дробей-показателей …,
2.4.	Подстановка .
2.5.	Подстановка ,
2.6.	Подстановка , .
2.7.	Подстановка , .
2.8. (дифференциальный бином), интегрируется только в трех случаях: а) р – целое (подстановка х = tk , где k – общий знаменатель дробей т и п); б) – целое (замена = tk, где k –знаменатель дроби р); в) – целое (замена = tk, где k –знаменатель дроби р).

Пример 7. Найти интегралы:

а) ; б); в) .

Решение.

а) Данный интеграл можно отнести к интегралам вида 2.1, поэтому выполним соответствующую подстановку. Напомним, что смысл замены в этом случае состоит в том, чтобы избавиться от иррациональности. А это означает, что заменить следует подкоренное выражение такой степенью новой переменной, из которой извлекались бы все имеющиеся под интегралом корни. В нашем случае это, очевидно :

Под интегралом получилась неправильная рациональная дробь. Интегрирование таких дробей предполагает, прежде всего, выделение целой части. Поэтому разделим числитель на знаменатель:

Тогда получаем , отсюда