Ответ на 22) При расчетах на прочность при кручении (также как и при растяжении) могут решаться три задачи:

а)      проверочный расчет – проверить, выдержит ли вал приложенную нагрузку;

б)      проектировочный расчет - определить размеры вала из условия его проч­ности;

в)      расчет по несущей способности - определить максимально допустимый крутящий момент.

При проверочном расчете на прочность рекомендуется следующий порядок расчета валов при кручении:

·        по схеме вала и действующим на него скручивающим моментам строят эпюру внутренних крутящих моментов по отдельным участкам;

·        выбирают материал для рассчитываемого вала и определяют для этого ма­териала допускаемое напряжение ;

·        для участка вала с максимальным по модулю значением крутящего момента записывают условие прочности при кручении

                                      

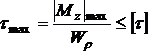
Проектировочный расчет проводится, исходя из условия прочности на основе следующего соотношения:

                                           

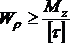
Для сплошного круглого сечения , отсюда можем записать вы­ражение для определения диаметра вала из условия его прочности:

                                   

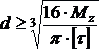
Определив размеры вала из условия прочности, проверяют вал на жесткость по формуле

,                                   

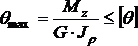где     - допустимый относительный угол закручивания вала.

Если данное условие не выполняется, то необходимо выбрать размеры вала из условия жесткости:

                                     

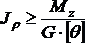
Учитывая, что для сплошного круглого сечения , можем запи­сать выражение для определения диаметра вала из условия его жесткости:

                                          

Окончательно выбирают диаметр d, удовлетворяющий условиям прочности и жесткости.

Примеры решения задач

Пример 1. На распределительном валу (рис. 26.3) установлены четыре шкива, на вал через шкив 1 подается мощность 12 кВт, которая через шкивы 2, 3, 4 передается потребителю; мощности распределяются следующим образом: Р2 = 8 кВт, Рз = 3 кВт, Р4 = 1кВ.

зал вращается с постоянной скоростью ω = 25 рад/с. Построить эпюру крутящих моментов на валу.

Рис.

Решение

1. Определяем моменты пар сил на шкивах.

Вращающий момент определяем из формулы мощности при вращательном движении P = mω, .

Момент на шкиве 1 движущий, а моменты на шкивах 2, 3, 4 - моменты сопротивления механизмов, поэтому они имеют противоположное направление. Брус скручивается между движущим моментом и моментами сопротивления. При равновесии момент движущий равен сумме моментов сопротивления:

; ;

; ;

; .

Пример 2. Выбрать рациональное расположение колес на валу (рис. 26.5). m1 = 280 Н·м; m2 = 140 Н·м; m3 = 80 Н·м.

Примечание. Меняя местами колеса (шкивы) на валу можно изменять величины крутящих моментов. Рациональным р. положением является такое, при котором крутящие моменты принимают минимальные из возможных значения.

mo = m1 + m2 + m3 = 280 + 140 + 80 = 500 Н·м.

Рассмотрим нагрузки на валу при различном расположении колес.

Из представленных вариантов наиболее рационально расположение шкивов в третьем случае, здесь значения крутящих моментов минимальны. Вывод: при установке шкивов желательно, чтобы мощность подавалась в середине вала и по возможности равномерно распределялась направо и налево.

Рис.

Первый вариант: .

Второй вариант: .

Третий вариант: .

Ответ на 23) Рациональные формы сечений при кручении.

Из двух сечений с одним и тем же полярным моментом сопротивления (или в случае некруглого сечения одним и тем же Wк), а следовательно, с одним и тем же допускаемым крутящим моментом, рациональным будет сечение с наименьшей площадью, т.е. обеспечивающее наименьший расход материала. Так как отношение Wp/A (или Wк/A) является величиной размерной, то для сравнения различных сечений удобно применять безразмерную величину  (при некруглом сечении ), которую можно называть удельным моментом сопротивления при кручении. Чем больше , тем рациональнее сечение. 

Таблица 2.2

Тип сечения

Швеллер . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Двутавр . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Прямоугольное сечение при a/b = 10 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . То же, a/b = 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Квадрат. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  Круглое сплошное сечение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Круговое кольцо при c = d/D = 0,5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . >> >> >> >> >> >> c = 0,9 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

0,04 - 0,05 0,05 - 0,07 0,1 0,18 0,21 0,28 0,37 1,16

Ответ на 24) Изгиб — вид деформации, при котором происходит искривление осей прямых брусьев или изменение кривизны осей кривых брусьев.

 Внутренние силовые факторы

Проведём плоское сечение через любую точку нейтральной оси балки и выделим участок балки по одну из сторон проведённого сечения. Условимся ось xпроводить вдоль нейтральной оси недеформированной балки, ось y – в плоскости изгиба, ось z – перпендикулярно плоскости изгиба.

При плоском поперечном изгибе внутренними силовыми факторами являются поперечная (перерезывающая) сила Qу и изгибающий момент Mz , которые определяются из уравнений равновесия, составленных для выделенного участка балки (рис. 2).

Рис. 2. Уравнения равновесия статики для выделенного участка балки

Поперечная сила в проведённом сечении равна сумме проекций на ось y всех внешних сил, действующих на выделенный участок балки (см. рис. 2).

Изгибающий момент в проведённом сечении равен сумме моментов всех действующих на выделенный участок балки внешних сил относительно оси z или (т.к. система внешних сил является плоской) сумме моментов всех внешних сил относительно центра тяжести проведённого сечения (см. рис. 2).

Ответ на 25) Эпюры поперечных сил и изгибающих моментов.

Построение эпюр поперечных сил и изгибающих моментов в балках

Стержень, работающий на изгиб, называется балкой. В сечениях балок, загруженных вертикальными нагрузками, возникают, как правило, два внутренних силовых фактора - поперечная сила  и изгибающий момент  .

Поперечная сила в сечении численно равна алгебраической сумме проекций внешних сил, приложенных по одну сторону от рассматриваемого сечения, на поперечную (вертикальную) ось.

Правило знаков для : условимся считать поперечную силу в сечении положительной, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, стремится повернуть данное сечение по часовой стрелке и отрицательной - в противном случае.

Схематически это правило знаков можно представить в виде

Изгибающий момент  в сечении численно равен алгебраической сумме моментов внешних сил, приложенных по одну сторону от рассматриваемого сечения, относительно оси x , проходящей через данное сечение.

Правило знаков для : условимся считать изгибающий момент в сечении положительным, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, приводит к растяжению в данном сечении нижних волокон балки и отрицательной - в противном случае.

Схематически это правило знаков можно представить в виде:

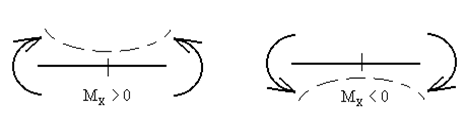
Следует отметить, что при использовании правила знаков для  в указанном виде, эпюра  всегда оказывается построенной со стороны сжатых волокон балки.

 

Консольные балки

При построении эпюр  и в консольных, или жестко защемленных, балках нет необходимости (как и в рассмотренных ранее примерах) вычислять опорные реакции, возникающие в жесткой заделке, но выбирать отсеченную часть нужно так, чтобы заделка в нее не попадала.

Пример 3. Построить эпюры  и (рис.6).

Рис. 6

Порядок расчета.

1. Намечаем характерные сечения.

2. Определяем поперечную силу  в каждом характерном сечении.

По вычисленным значениям строим эпюру .

3. Определяем изгибающий момент  в каждом характерном сечении.

По вычисленным значениям строим эпюру , причем, на участке под распределенной нагрузкой эпюра будет криволинейной (квадратная парабола). Выпуклость кривой на этом участке всегда обращена навстречу распределенной нагрузке.

Дифференциальные зависимости между

Указанные зависимости используются при построении эпюр , поэтому приведем их здесь без соответствующего вывода, который дается в лекционном курсе.

Пример 4. Построить эпюры  (рис.7).

В данном случае для правильного построения эпюры  необходимо использовать приведенные выше дифференциальные зависимости.

Порядок расчета.

1. Намечаем характерные сечения.

2. Определяем поперечные силы в характерных сечениях.

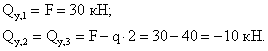
Строим эпюру .

Характер эпюры, то есть тот факт, что эпюра  пересекает ось, говорит о том, что в этом сечении момент  будет иметь экстремальное значение. Действительно, пересечение эпюры с осью z означает, что в этом сечении , а из курса математики известно, что если производная функции равна нулю, то сама функция в данной точке имеет экстремальное значение.

Для определения положения “нулевого” сечения необходимо величину расположенной слева от него ординаты эпюры  разделить на интенсивность распределенной нагрузки q:

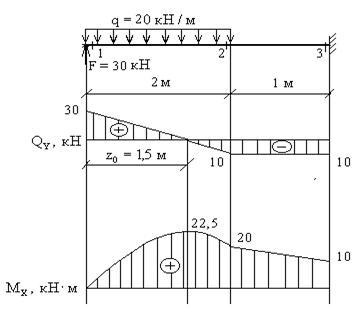
Рис. 7

Определяем изгибающие моменты в характерных сечениях.

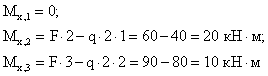
4. Вычисляем экстремальное значение изгибающего момента в сечении, где : 

Ответ на 26) Нормальные напряжения при изгибе.