Квартили и децили.

По аналогии с нахождением медиан в вариационных рядах можно отыскать значение признака у любой по порядку единицы ранжированного ряда. Так в частности можно найти значение у единиц делящих ряд на 4 равные части на 10 и т.п.

Варианты, которые делят ранжированный ряд на 4, называют квартилями.

При этом различают: нижний (или первый) квартиль (Q₁) – значение признака у единицы у единицы ранжированного ряда, делящей совокупность в соотношении ¼ к ¾ и верхний (или третий) квартиль(Q₃) – значение признака у единицы ранжированного ряда, делящий совокупность в соотношении ¾ к ¼.

Второй квартиль, есть медиана Q₂ = Ме нижний и верхний квартили в интервальном ряду рассчитывается по формуле аналогично медиане.

для нижнего

для верхнего

где x_o – нижняя граница интервала, содержащего квартиль (нижний и верхний)

f¹_Q1-1 – накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль.

f¹_Q3-1 – то же для вернего квартиля.

F_Q1; F_Q3 – частоты квартильных интервалов (нижнего и верхнего).

Интервалы, в которых содержатся Q₁ и Q₃ определяют по положенным частотам (или частостям).

Пример.

Вал.прод., т.р. х	Число предприятий f	Накопленная частота f1
До 50 50-100 100-150 150-200 200-250 250-300 > 300	3 6 10 21 33 18 9	3 9 19 40 73 91 100

Из примера находим первый квартиль

Q₁ =т.е. интервал 150-200

это означает, что у ¼ всех предприятий выпуск продовольствия не превышает 164,3 т.р.

кроме квартилей рассчитывают децили – варианты, делящие ранжированный ряд на 10 равных частей.

Обозначаются они через D, первый дециль D₁ делит ряд в соотношении 1/10 и 9/10, второй D₂ – 2/10 и 8/10

и медиана, и квартили, и децили принадлежат к так называемым порядковым статистикам, под которым понимают вариант, занимающий определенное порядковое место в ранжированном ряду.

Понятие о моментах распределения.

В математической статистике моментом k-того прядка называется средняя арифметическая из k- той степени отложений отдельных вариантов от некоторой постоянной величины А, т.е. если обозначить момент к-того порядка

Через Мк, то в общем виде

в статистике находят применение моменты первых четырех.

Теоретические кривые распределения.

Графическое изображение вариационного ряда дает представление о форме распределения. Однако судить о закономерностях данного эмпирического распределения по полигону или гистограмме рискованно, т.к. оно зависит от ряда причин, и частности от числа исследованных единиц.

Характерные черты распределения проявляются при росте числа наблюдений.

По мере увеличения числа наблюдений и уменьшения величины интервала для непрерывных признаков ступенчатость гистограммы или ломанность полигона будут сглаживаться и приближаться к некоторой плановой кривой.

Имея графическое изображение эмпирического вариационного ряда, можно представить тот предел в виде сплошной плавной линии, к которой стремится данная гистограмма или полигон при увеличении числа наблюдений и уменьшение величины интервала.

Этот предел в виде сплошной плавной линии называют кривой распределения.

Кривая распределения может рассматриваться как некая теоретическая (вероятностная) форма распределения, свойственная той или иной совокупности в конкретных условиях места и времени. Если кривая описана математически, т.е. выражена уравнением с определенными параметрами, то она более точно отражает закономерности того или иного распределения.

Имея дело с эмпирическими распределениями можно предположить, что данному эмпирическому распределению соответствует характерное для него теоретическая кривая.

Знание формы теоретической кривой может быть использовано в различных практических расчетах, прогнозах. Поэтому при изучении закономерностей распределение нужно определить тип кривой распределения, установить по эмпирическим данным ее параметры, рассчитать по найденному уравнению

Теоретические частоты (построить эту теоретическую кривую), проверить на сколько эмпирические частоты близки к предполагаемым теоретическим.

Кривая нормального распределения и ее построение по эмпирическим данным.

Среди различных кривых распределения особое место занимает нормальное распределение.

Нормальное распределение на графике представляет собой симметрическую колоколообразную кривую, имеющую максимум в точке соответствующей средней арифметической ряда. Эта же точка является модой и медианой ряда.

Точки перегиба у нормальной кривой на расстоянии от средней арифметической.

график

Кривая нормального распределения выражается следующим уравнением:

где у ордината кривой распределения П=3,14 е = 2,182… -основание натурального логарифма.

Отклонение отдельных вариантов от средней арифметической нормируют по

и именуют нормированным отклонением

если в приведенной выше формуле кривой нормального распределения произвести соответственную замену, то уравнение примет вид

Как видно из уравнения, два параметра – средняя арифметическая и средне квадратическое отклонение- определяют очертание симметричной кривой нормального распределения.

В зависимости от их значения она может иметь разный центр группирования, быть более удлиненной или сжатой.

Если площадь, ограниченную кривой нормального распределения, принять за 1 или за 100%, то можно рассчитать площадь, заключенную между кривой и е двумя ординатами.

Установлено, что площадь между ординатами, проведенными на расстояние с каждой стороны от средней арифметической, составляет 0,683 всей площади.

Это означает, что 68,3% всех исследованных единиц (частот) отклоняются от средней арифметической не более чем на , т.е. находятся в пределах ().

S, заключенная между ординатами, проведенными на расстояние 2в одну другую сторону от средней арифметической, составляет 0,954, т.е. всех единиц совокупности находятся в пределах. Это так называемое правило 3-сигментов, характерное для нормального распределения.

Нормальное распределение характерно для явлений в области биология и техники.

В экономике чаще встречаются умеренно ассиметричные распределения.

Тем не менее кривая нормального распределения имеет определенное значение в анализе вариационных рядов и в теории выборочного метода.

Есть несколько способов построения кривой нормального распределения по эмпирическим данным, если есть основание предположить близость данного распределение к нормальному. По одному из этих способов теоретические частоты (m¹) отыскивается

где - табулированная величина, отыскиваемая по отклонениям t, а Nh/- константа, на к умножаются значенияи которая определяет теоретические частоты исходя из общей численности единиц совокупности и числа выделяемых групп. Последовательность расчета следующая:

1 находим

2 находим

3 находим нормированное отклонение каждого варианта от средней арифметической

4 для найденных t по таблице определяем

5 расчитаем константу

6 каждое значение умножаем на константу

результаты умножения (после округления до целых чисел) будут искомыми частотами (m^/) теоретической кривой нормального распределения.

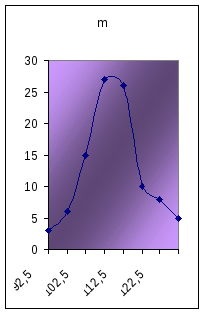
Пример 100предприятиц по % выполнения плана по валовой продукции (х). показано на рис распределение и теоретическое, и эмпирическое.

Середина интервала х	m				63=m/
92,5 97,5 102,5 107,5 112,5 117,5 122,5 127,5	3 6 15 27 26 10 8 5	-17,7 -12,7 -7,7 -2,5 2,5 7,3 12,3 17,3	-2,21 -1,59 -0,96 -0,31 0,29 0,91 1,54 2,16	0,0347 0,1127 0,2516 0,3802 0,3825 0,2637 0,1219 0,0387	2,1861 2 7,1001 7 15,85 16 23,95 24 24,097 24 16,61 17 7,68 8 2,44 2
Итого	100