
Чубаров лаба 3
.docxФедеральное государственное автономное
образовательное учреждение
высшего профессионального образования
«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
Институт управления бизнес-процессами и экономики
Кафедра бизнес-информатики
ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №3
По дисциплине «Методы моделирования и прогнозирования экономики»
Вариант 6
Студент УБ 11-01 __________ Ивкина В.А.
Руководитель __________ Чубаров А.В.
Красноярск 2013
Оглавление
Теоретические сведения 3
Постановка задачи 6
Алгоритмическая часть 7
Заключение 9
Теоретические сведения
Транспортная задача - задача о поиске оптимального распределения поставок однородного товара к потребителям от поставщиков при известных тарифах на перевозку между пунктами отправления и назначения. Является задачей линейного программирования.
Некоторый однородный
продукт сосредоточен у m
поставщиков (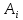 ),
где i=1,
),
где i=1,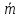 ,
в количестве
,
в количестве
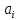 единиц. Требуется перевезти продукт к
n
потребителям (
единиц. Требуется перевезти продукт к
n
потребителям (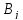 ),
где j=1,
),
где j=1,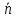 ,
в количестве
,
в количестве
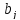 единиц. Также известна стоимость
перевозки
единиц. Также известна стоимость
перевозки
 единицы груза от i-го
поставщика к j-му
потребителю.
единицы груза от i-го
поставщика к j-му
потребителю.
Необходимо составить такой план перевозок, чтобы все грузы были вывезены, все заявки исполнены и, чтобы суммарная стоимость перевозок была минимальной.
Модель транспортной задачи выглядит следующим образом.
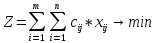 (1)
(1)
Z - целевая функция;
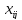 -
количество единиц груза, перевозимого
от i-го
поставщика к j-му
потребителю;
-
количество единиц груза, перевозимого
от i-го
поставщика к j-му
потребителю;
 - стоимость перевозки
единицы груза от i-го
поставщика к j-му
потребителю;
- стоимость перевозки
единицы груза от i-го
поставщика к j-му
потребителю;
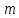 - количество
поставщиков;
- количество
поставщиков;
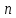 - количество
потребителей.
- количество
потребителей.
Система ограничений задачи состоит из двух групп уравнений. Первая группа из m уравнений описывает тот факт, что запасы всех m поставщиков вывозятся полностью:
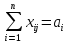 ,
где i=1,
,
где i=1,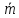 (2)
(2)
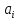 - количество единиц
продукций у m
поставщиков.
- количество единиц
продукций у m
поставщиков.
Вторая группа из n уравнений выражает требование полностью удовлетворить запросы всех n потребителей:
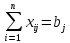 ,
где j=1,
,
где j=1,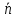 (3)
(3)
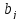 -
количество единиц продукций, которое
необходимо перевезти к n
потребителям.
-
количество единиц продукций, которое
необходимо перевезти к n
потребителям.
В рассмотренной модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарным запросам потребителей, то есть:
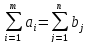 (4)
(4)
При этом, соблюдается условие неотрицательности:
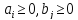 ,
,
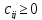 ,
,
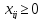 (5)
(5)
Такая задача называется задачей с правильным балансом, а ее модель - закрытой. Если же это равенство не выполняется, то задача называется задачей с неправильным балансом, а ее модель - открытой.
Если
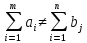 ,
то транспортная
задача называется открытой моделью.
,
то транспортная
задача называется открытой моделью.
Решение выполняется переходом к закрытой модели.
-
Если
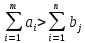 ,
то вводится фиктивный потребитель
,
то вводится фиктивный потребитель
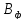 ,
заявка которого
,
заявка которого
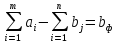 ,
тарифы
,
тарифы
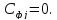 Занятые
клетки столбца
Занятые
клетки столбца
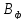 соответствуют наименее выгодным
поставщикам. Часть запасов остается
невывезенным.
соответствуют наименее выгодным
поставщикам. Часть запасов остается
невывезенным. -
Если
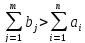 ,
то вводится фиктивный поставщик
,
то вводится фиктивный поставщик
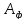 ,
запасы которого равны
,
запасы которого равны
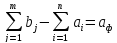 ,
тарифы
,
тарифы
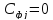 .
Занятые клетки строки
.
Занятые клетки строки
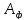 соответствуют наименее выгодным
потреблениям, их потребности выполняются
полностью.
соответствуют наименее выгодным
потреблениям, их потребности выполняются
полностью.
Существует несколько простых схем построения первоначального опорного плана транспортной задачи:
-
Метод северо-западного угла;
-
Метод минимальной стоимости;
-
Метод двойного предпочтения.
Рассмотрим самый простой способ решения транспортной задачи - Метод северо-западного угла. Метод состоит в последовательном переборе строк и столбцов транспортной таблицы, начиная с левого столбца и верхней строки, и выписывании максимально возможных отгрузок в соответствующие ячейки таблицы так, чтобы не были превышены заявленные в задаче возможности поставщика или потребности потребителя.
Постановка задачи
-
Изучить алгоритм решения транспортных задач.
-
Изучить функции, использующиеся в Excel при решении транспортных задач.
-
Определить суммарные издержки на поставку товара.
-
Найти оптимальный план закрепления поставщиков за потребителями.
-
Проанализировать итоговые данные.
Исходные данные (табл.1):
|
|
40 |
30 |
90 |
80 |
50 |
|
60 |
4 |
2 |
3 |
4 |
1 |
|
90 |
2 |
4 |
3 |
5 |
6 |
|
140 |
6 |
5 |
4 |
6 |
2 |
Алгоритмическая часть
-
Заполним ячейки исходными данными.
-
Получаем нули в соответствующих ячейках, суммируя ячейки по стокам и столбцам. Для этого обозначаем соответствующую ячейку, выбираем функцию «СУММ», выделяем необходимые аргументы в столбце, как показано на рисунке 1. Проделываем аналогичные операции для строк.
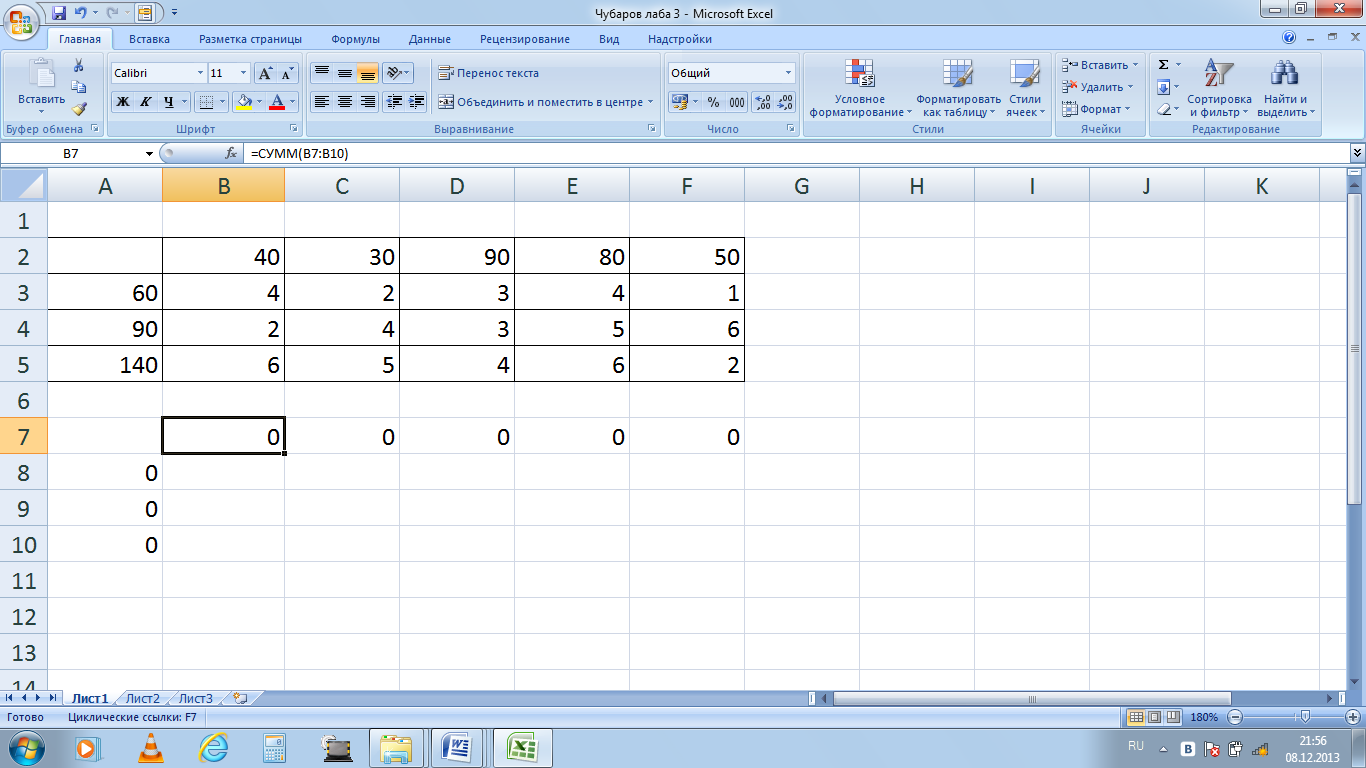
Рисунок 1 - Использование математической функции «СУММ»
-
Для задания целевой функции воспользуемся функцией Excel - «СУММПРОИЗВ». Зададим целевую ячейку - В12 и применим данную функцию
-
В результате операции получаем в целевой ячейке В13 = 0.
-
Для нахождения оптимального варианта стоимости перевозок воспользуемся функцией поиск решений.
-
В появившемся окне в поле «Установить целевую функцию» выбираем ячейку А13; В поле «Изменяя ячейки» выделяем область
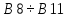 ;
Устанавливаем флажок в поле «Минимальному
значению»;
Добавим
соответствующие ограничения (см. рисунок
2)
;
Устанавливаем флажок в поле «Минимальному
значению»;
Добавим
соответствующие ограничения (см. рисунок
2)
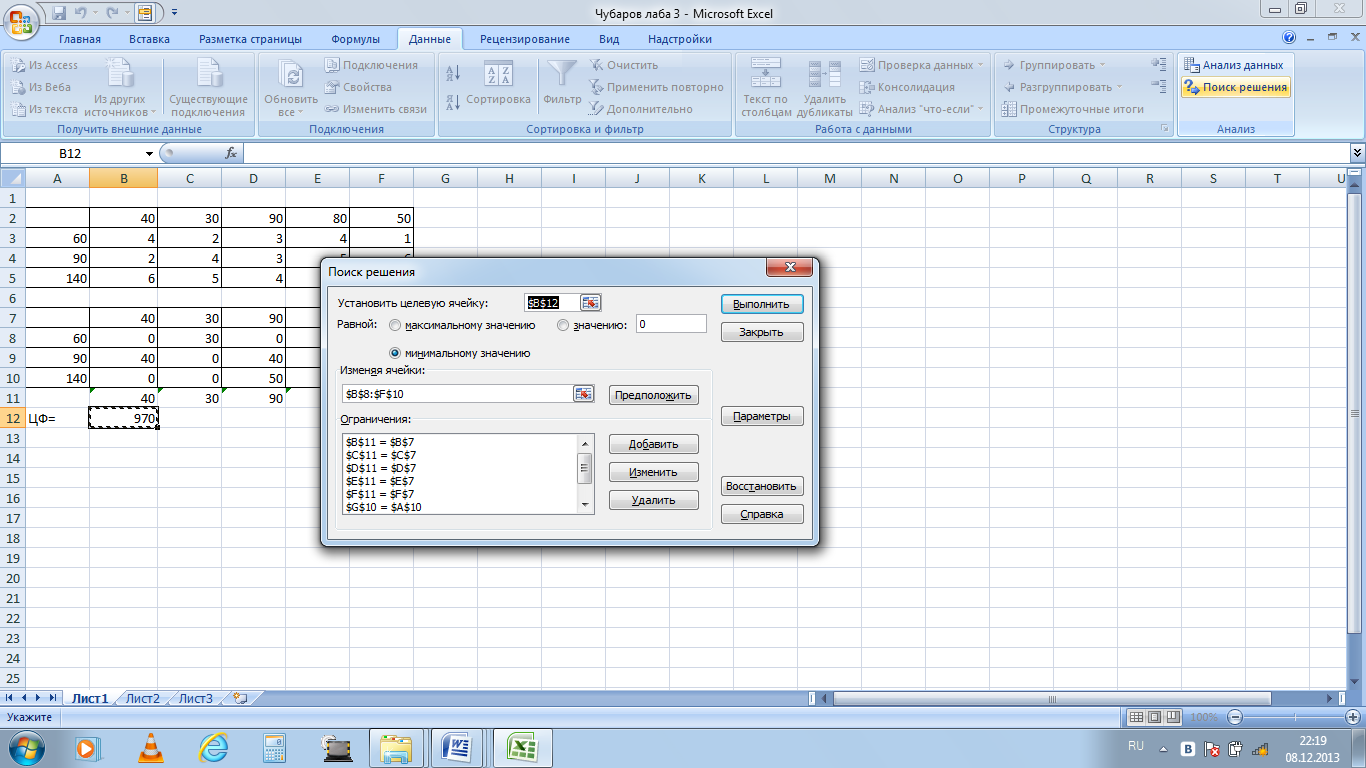
Рисунок 2 - использование функции Поиск решений
После того, как все ограничения нами учтены, нажимаем «Выполнить».
Появится диалоговое окно Результаты поиска решений, в котором предлагается сохранить найденное решение. Нажимаем «ОК».
Результат полученных вычислений представлен на рисунке 3. Оптимальной стоимость перевозок, стоимостью 970 ед. достигается при представленном закреплении поставщиков за потребителем.

Рисунок 3 - Оптимальная стоимость перевозок
Заключение
В ходе выполнения лабораторной работы была освоена методика решения транспортных задач при помощи программы MS Excel, использования таких функций программы, как «СУММ», «СУММПРОИЗВ» и «Поиск решений».
В результате полученных вычислений найден оптимальный план, при котором минимальные суммарные затраты на перевозку груза равны 970 ед.
