
Постановка задачи
Определить значение коэффициентов
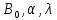 для метода Койка, при помощи метода
наименьших квадратов.
для метода Койка, при помощи метода
наименьших квадратов.Рассчитать коэффициенты с распределенными лагами.
Сравнить уравнения, полученные по методу Койка и по методу последовательного увеличения лагов.
Исходные данные (табл.1):
|
t |
Yt |
It |
|
1 |
13800 |
3000 |
|
2 |
13800 |
3000 |
|
3 |
13800,69 |
3000 |
|
4 |
13043,48 |
2700,48 |
|
5 |
13298 |
2800 |
|
6 |
13228 |
3200 |
|
7 |
13688,16 |
3289 |
|
8 |
13335 |
2500 |
|
9 |
12626,27 |
2560,54 |
|
10 |
14614 |
2760 |
|
11 |
14444 |
2680 |
|
12 |
9887 |
1700 |
|
13 |
9570,231 |
1890,231 |
|
14 |
9781,08 |
2000 |
|
15 |
9975,847 |
1984 |
|
16 |
10712,38 |
1780,378 |
|
17 |
11161 |
1900 |
|
18 |
12181,15 |
1900 |
|
19 |
11986,26 |
1973 |
|
20 |
11353,51 |
2000,907 |
|
21 |
13524 |
2200 |
|
22 |
13769,06 |
2389 |
|
23 |
13800 |
2500 |
|
24 |
13019,74 |
1680 |
|
25 |
14045 |
1716 |
|
26 |
15210,67 |
2269,672 |
|
27 |
15037 |
2100 |
|
28 |
14588,8 |
1731,3 |
|
29 |
16876,9 |
2034,9 |
|
30 |
17671,4 |
2728,3 |
|
31 |
16843,4 |
3310,4 |
Алгоритмическая часть
Воспользовавшись функцией Excel «Анализ данных
регрессия», найдем необходимые коэффициенты уравнения преобразования Койка.
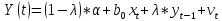 ,
(13)
,
(13)
Получим результат значения коэффициентов (табл.1):
|
Α(1-λ) |
1400,505 |
|
Β0 |
0,5421 |
|
λ |
0,8043 |
|
α |
7151,49 |
Полученное уравнение выглядит следующим образом:
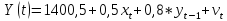 ,
(14)
,
(14)
На основе вычисленных параметров рассчитаем коэффициенты
системы с распределенными лагами, при K=5, для последующей оценки модели методом последовательного увеличения лагов (табл.3).
|
|
0,5421057 |
|
|
0,4360188 |
|
|
0,3506925 |
|
|
0,2820641 |
|
|
0,2268658 |
|
|
0,1824695 |
Таблица 3 - коэффициенты с распределенными лагами
Для составления модели составим таблицу- распределенные лаговые переменные, K=5 (табл.4):
|
t |
It |
It-1 |
It-2 |
It-3 |
It-4 |
It-5 |
|
1 |
3000 |
|
|
|
|
|
|
2 |
3000 |
3000 |
|
|
|
|
|
3 |
3000 |
3000 |
3000 |
|
|
|
|
4 |
2700,48 |
3000 |
3000 |
3000 |
|
|
|
5 |
2800 |
2700,48 |
3000 |
3000 |
3000 |
|
|
6 |
3200 |
2800 |
2700,48 |
3000 |
3000 |
3000 |
|
7 |
3289 |
3200 |
2800 |
2700,48 |
3000 |
3000 |
|
8 |
2500 |
3289 |
3200 |
2800 |
2700,48 |
3000 |
|
9 |
2560,54 |
2500 |
3289 |
3200 |
2800 |
2700,48 |
|
10 |
2760 |
2560,54 |
2500 |
3289 |
3200 |
2800 |
|
11 |
2680 |
2760 |
2560,54 |
2500 |
3289 |
3200 |
|
12 |
1700 |
2680 |
2760 |
2560,54 |
2500 |
3289 |
|
13 |
1890,231 |
1700 |
2680 |
2760 |
2560,54 |
2500 |
|
14 |
2000 |
1890,231 |
1700 |
2680 |
2760 |
2560,54 |
|
15 |
1984 |
2000 |
1890,231 |
1700 |
2680 |
2760 |
|
16 |
1780,378 |
1984 |
2000 |
1890,231 |
1700 |
2680 |
|
17 |
1900 |
1780,378 |
1984 |
2000 |
1890,231 |
1700 |
|
18 |
1900 |
1900 |
1780,378 |
1984 |
2000 |
1890,231 |
|
19 |
1973 |
1900 |
1900 |
1780,378 |
1984 |
2000 |
|
20 |
2000,907 |
1973 |
1900 |
1900 |
1780,378 |
1984 |
|
21 |
2200 |
2000,907 |
1973 |
1900 |
1900 |
1780,378 |
|
22 |
2389 |
2200 |
2000,907 |
1973 |
1900 |
1900 |
|
23 |
2500 |
2389 |
2200 |
2000,907 |
1973 |
1900 |
|
24 |
1680 |
2500 |
2389 |
2200 |
2000,907 |
1973 |
|
25 |
1716 |
1680 |
2500 |
2389 |
2200 |
2000,907 |
|
26 |
2269,672 |
1716 |
1680 |
2500 |
2389 |
2200 |
|
27 |
2100 |
2269,672 |
1716 |
1680 |
2500 |
2389 |
|
28 |
1731,3 |
2100 |
2269,672 |
1716 |
1680 |
2500 |
|
29 |
2034,9 |
1731,3 |
2100 |
2269,672 |
1716 |
1680 |
|
30 |
2728,3 |
2034,9 |
1731,3 |
2100 |
2269,672 |
1716 |
|
31 |
3310,4 |
2728,3 |
2034,9 |
1731,3 |
2100 |
2269,672 |
Таблица 4 - распределенные лаговые переменные.
На основе полученных данных рассчитаем теоретические значения результативного признака Y(t) - Объем валового регионального продукта, используя следующее уравнение:
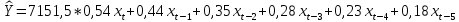 ,
(15)
,
(15)
Сравним какое из полученных выражений наиболее точно приближает Y(t). Для этого построим график по исходным и полученным теоретическим значениям (рис.1):
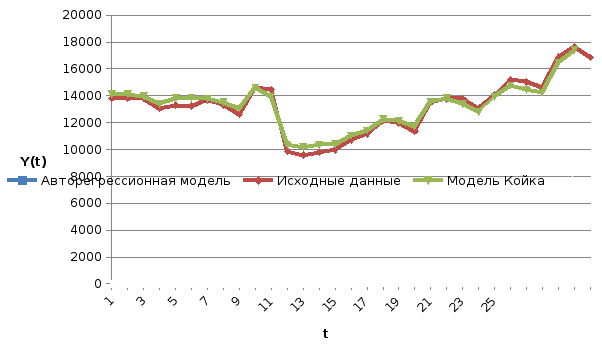
Рисунок 1 - Выбор оптимальной модели описания исходных данных
На графике видно, что модель Койка лучшим образом описывает исходные значения существующей зависимости.

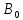
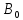 *
*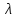 (
(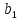 )
)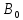 *
*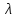 ^2 (
^2 (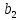 )
)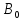 *
*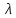 ^3 (
^3 (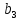 )
)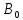 *
*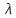 ^4 (
^4 (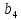 )
)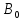 *
*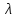 ^5 (
^5 (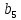 )
)