Ряды Маклорена

Если в ряде Тейлора , то получим ряд Маклорена по степеням х.

Остаточный член

Получим разложение некоторых элементарных функций в ряд Маклорена и найдём интервалы сходимости этих рядов.

1)

Интервал сходимости этого ряда найдем непосредственно по признаку Даламбера.

Интервал сходимости

При любом х ряд сходится по признаку Даламбера.

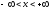- интервал сходимости.

2)

т.к семейство производных любого порядка равномерно ограничено приинтервал сходимости

3)

- интервал сходимости.

4) Биномиальное разложение

- интервал сходимости.

5) f(x)=ln(1+x)

Воспользуемся предыдущим биномиальным разложением:

проинтегрируем почленно на отрезке

снимем модуль, т.к 1+х>0

- можно показать.

6) f(x)=arctgx

воспользуемся биномиальным разложением и заменим

проинтегрируем на

Приближенное вычисление с помощью рядов Тейлора и Маклорена

С помощью рядов Тейлора и Маклорена можно приближенно вычислять значения функций. Для этого функцию раскладывают в степенной ряд Тейлора и заменяем сумму ряда его частичной суммой. Возникающую при этом погрешность (остаточный член) оценивают следующим образом:

1) если ряд знакочередующийся, то последствию из теоремы Лейбница, для знакочередующихся рядов, остаточный член не превосходит модуля 1 отбрасываемого члена.

2) если ряд знакоположительный, то остаточный член оценивается непосредственно.

Примеры:

1)

2)

3)

Тригонометрические ряды Фурье

Тригонометрическим рядом Фурье для функции f(x) на интервале от

называется ряд вида:

, где

Условия разложимости:

Пусть f(x):

1) Периодическая с

2) Кусочномонотонна

3) Ограничена на функциюf(x) можно разложить в ряд Фурье на , который сходится к этой функции во всех точках непрерывности, в точках разрыва сумма ряда равна полусумме левого и правого предела функции.

Замечание: Основная трудность построения рядов Фурье в вычислении интегралов.

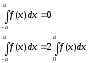
Пример:

Разложить функцию f(x)=x на в тригонометрический ряд Фурье, сделать чертеж.

Тригонометрический ряд Фурье от четных и нечетных функций и на интервале

Если f(x) – четная

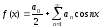- ряд Фурье по косинусам.

Если f(x) – нечетная

- ряд Фурье по синусам.

Если функция f(x) определена на интервале ее нужно продолжить (доопределить) на интервали только потом построить ряд Фурье. Продолжение функции на интервалдолжно быть естественным, лучшее продолжение – четное или нечетное.

Четное продолжение:

Нечетное продолжение:

Пример:

Разложить функцию f(x)=1 на 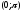в тригонометрический ряд Фурье продолжив её нанечетным образом.

Тригонометрический ряд Фурье на интервале

Пусть f(x) определена на и период

Замена: определена наи с периодоми ее можно разложить в тригонометрический ряд Фурье :

, где

Замена:

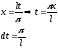
t
x

- тригонометрический ряд Фурье по на

Условия разложимости функции в ряд Фурье на интервале аналогично условиям на интервале

Пример:

f(x)=2x+3 разложить в ряд Фурье

Ряды Фурье на интервале

Если f(x) кусочно-монотонна и ограничена на интервале , то её нужно продолжить на интерваллибо чётным, либо нечётным образом.

Для чётного продолжения:

Для нечетного продолжения: