Министерство образования и науки российской федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Национальный исследовательский ядерный университет «мифи»

Волгодонский инженерно-технический институт - филиал НИЯУ МИФИ

Конспект лекций

по теме:

«Функциональные ряды»

Волгодонск

Функциональные ряды

Определени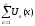е: , где 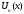- функции переменной х называетсяфункциональным рядом.

При некоторых значениях х функциональный ряд сходится, при других значениях х – расходится.

Определение: Множество значений переменной х, при которых функциональный ряд 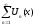- сходится, называетсяобластью сходимости функционального ряда. Задача нахождения области сходимости функционального ряда является весьма трудной, хотя для некоторых рядов область сходимости найти легко.

Пример:

1)

2)

Равномерная сходимость функционального ряда

Определение: Функциональный ряд 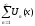называетсямажорируемым на [a;b], если существует сходящийся числовой ряд из 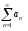, так что…при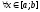. При этом числовой ряд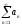-мажоранта функционального ряда .

Пример:

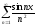
Как и числовой ряд ряд функциональный может быть записан в виде:

; где 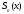-n частичная сумма ряда, -n остаток ряда.

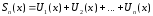
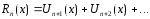
Определение: 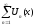называется равномерно сходящимся на [a;b], если 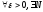начиная с которого выполняется неравенство, при любом, т.е- равномерно сходится на [a;b] если 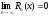, для.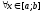

Замечание: существуют сходящиеся функциональные ряды, которые не сходятся равномерно.

Признак Вейерштрасса о равномерной сходимости функционального ряда

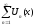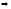
Если функциональный ряд на [a;b] мажорируется сходящимся числовым рядом равномерно сходится на этом отрезке.

Свойства равномерно сходящегося функционального ряда:

Теорема 1: Если функциональный ряд ,составленный из непрерывных функций на [a;b], равномерно сходится на этом отрезке, то сумма ряда S(x) – тоже будет непрерывной функцией на [a;b].

Рассмотрим функциональный ряд

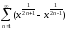
Этот ряд состоит из непрерывных степенных функций , n частичная сумма ряда

Вычислим сумму ряда:

- сходится, но S(x) – является разрывной функцией.

Вывод: S(x) не сходится равномерно.

Теорема 2: Если функциональный 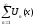равномерно сходится на [a;b] его можно почленно интегрировать на любом отрезке входящем в [a;b] условием интегрируемости является непрерывность функции .

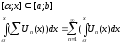
Пример:

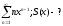
Теорема 3: Если функциональный 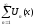равномерно сходится на [a;b] и ряд составленный из производных 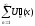тоже равномерно сходится на [a;b] функциональный ряд можно почленно дифференцировать.

Пример:

Степенные ряды

Определение: Степенным рядом называется ряд вида , где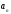- коэффициент степенного ряда, зависит отn и не зависит от х.

Степенной ряд является частным случаем функционального ряда, поэтому естественно поставить вопрос об области сходимости степенного ряда и его равномерной сходимости. Ответ на вопрос какой вид имеет область сходимости степенного ряда дает теорема Абеля.

Теорема Абеля:

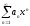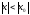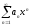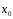
Если сходится в точке он сходится во всех точках, удовлетворяющих неравенству. Еслирасходится в точке 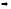он расходится во всех точках, удовлетворяющих неравенству.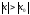

Доказательство:

Пусть 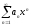сходится в точке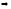будет сходится рядпо необходимому признаку сходимости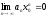числовая последовательность- ограничена, т.е существует числоM>0, что сразу для всехn.

Возьмем любое х удовл. 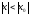и рассмотрим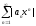из абсолютных величин.

Оценим общий член этого ряда:

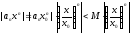
Ряд из членов геометрической прогрессии 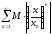со знаменателемсходится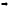исходный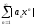тоже сходится поI признаку сравнения, т.к его члены меньше членов сходящегося ряда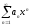сходится абсолютно.

Пусть расходится в точке.

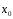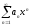Возьмем любое х удовл. , нужно доказать, чторасходится при любом х, удовлетворяющем.

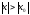Предположим противное: 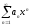- сходится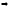по 1 части доказательства он будет сходится в точке.

Полученное противоречие доказывает теорему.

Конец доказательства.

Из теоремы Абеля что если степеннойсходится в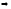он сходится в точке удовлетворяющей неравенству: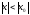

_{сходится расходится}

^{расходится} . .

⁰

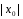
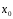Если расходится в точке, тогда он расходится

Вывод: существует интервал с центром в точке 0, радиусом R, внутри которого степенной ряд сходится, и вне которого расходится. Такой интервал называется интервалом сходимости степенного ряда, а R – радиусом сходимости степенного ряда. Укажем метод нахождения интервала сходимости.