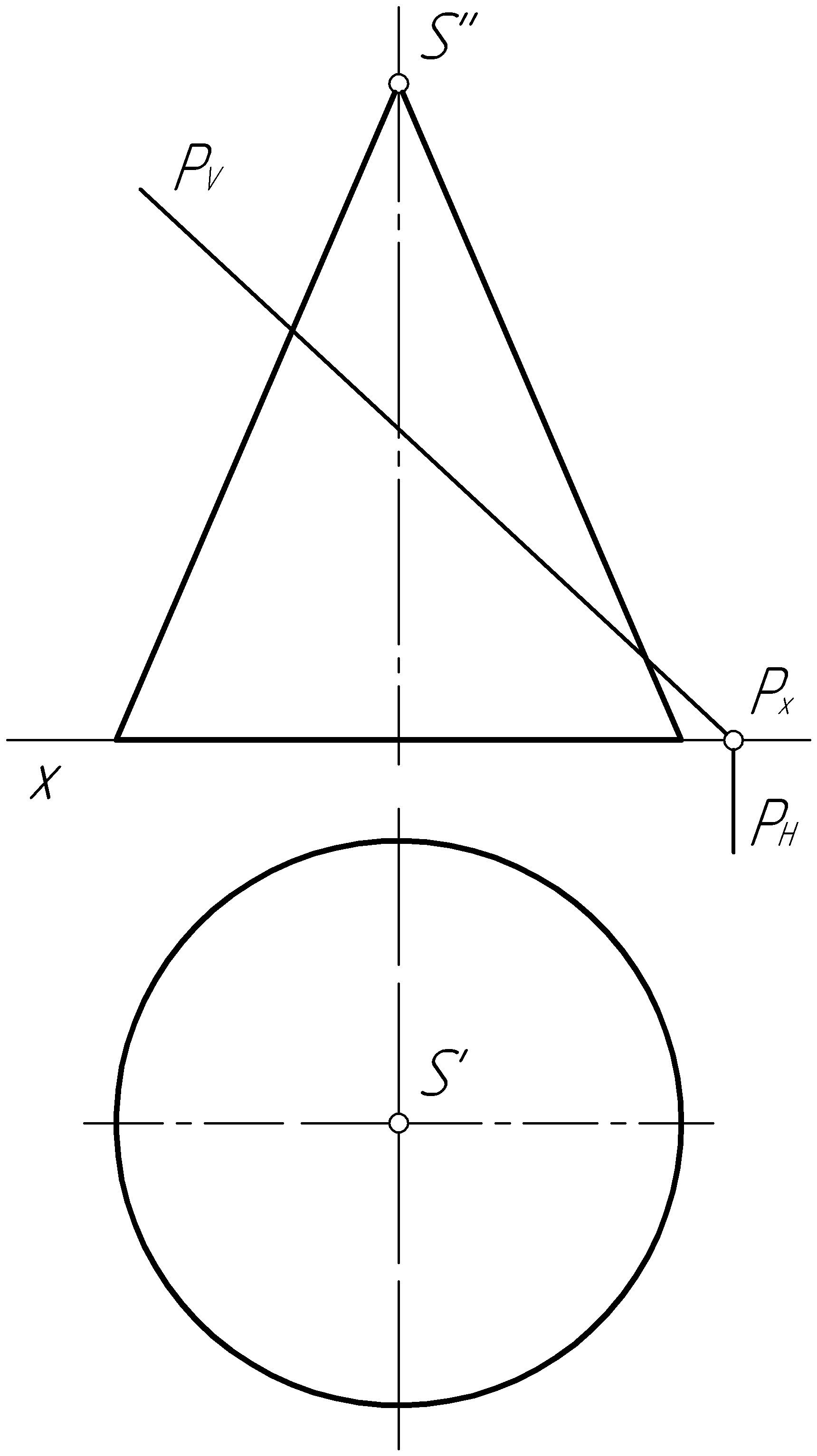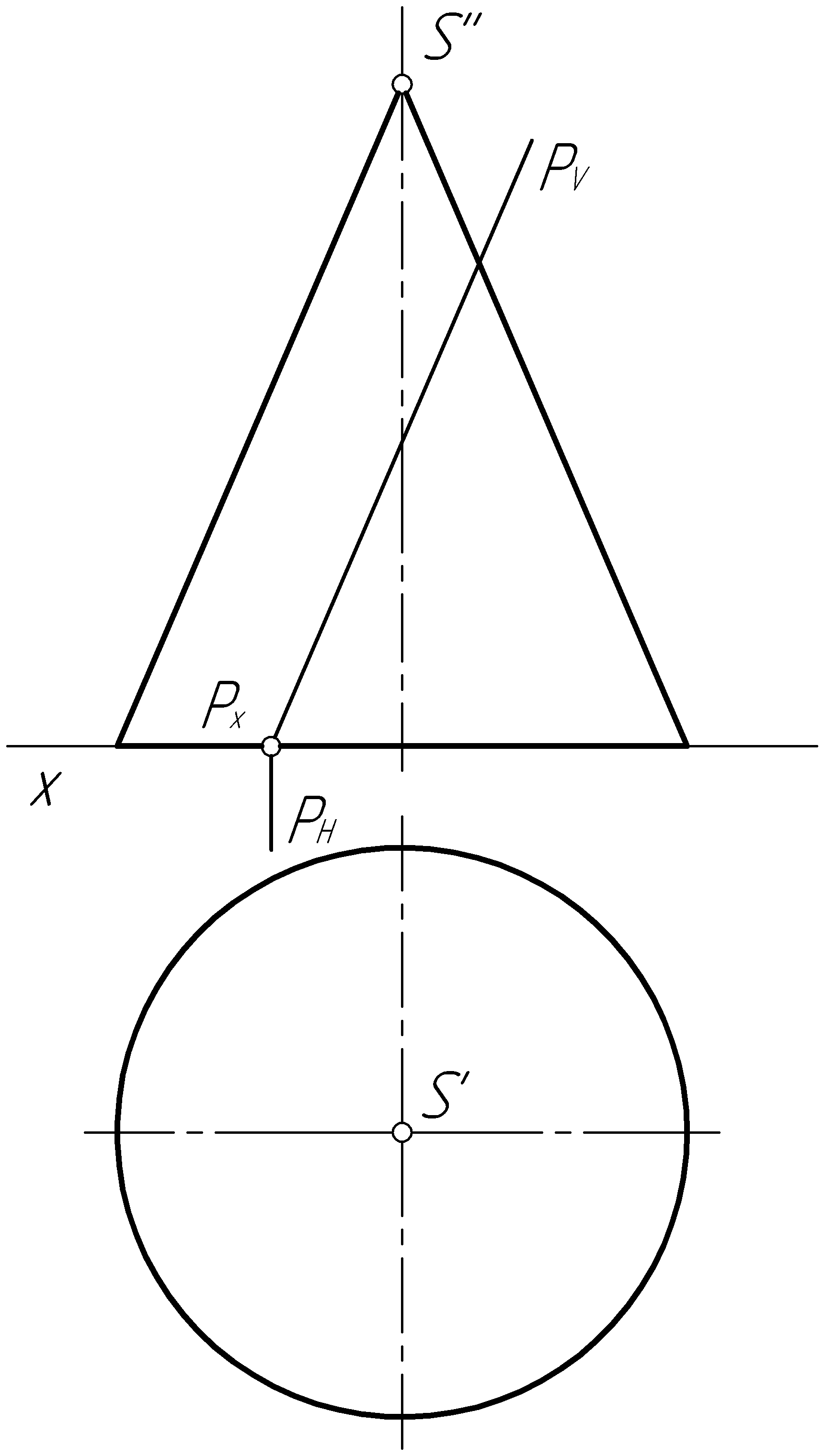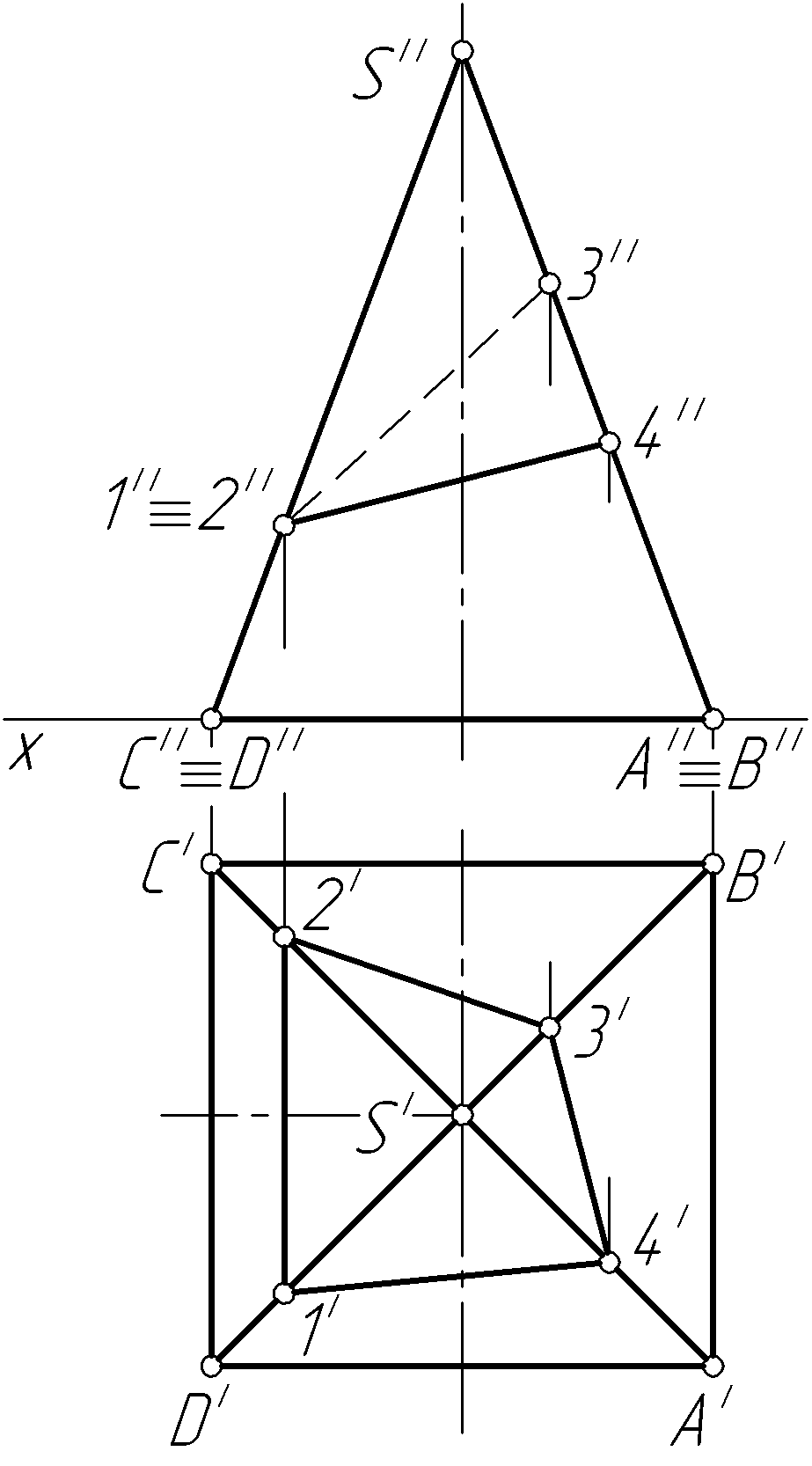Пересечение поверхностей плоскостью. Развертывание поверхностей Примеры решения задач

Линия пересечения поверхности плоскостью является плоской кривой, лежащей в плоскости сечения. Для построения этой линии строят точки, принадлежащие одновременно поверхности и секущей плоскости, соединив которые получают линию пересечения. Среди точек этой линии есть точки, которые выделяются своим особым положением. Их называют опорными. Это точки: расположенные на крайних образующих поверхности и являющиеся границами видимости на чертеже; наиболее или наименее удаленные от наблюдателя; определяющие построение некоторых линий пересечения. Для построения этих точек применяют различные приемы. Все остальные точки называются общими или произвольными и для них используют одни и те же приемы построения.

Основной способ построения заключается в следующем:

1) вводится вспомогательная плоскость, которая должна пересекать и поверхность, и плоскость по некоторым линиям;

2) при пересечении этих линий между собой получают точки, принадлежащие и поверхности, и плоскости сечения, т.е. точки, составляющие линию пересечения поверхности и плоскости.

Таким способом определяют общие точки, а также и некоторые опорные точки. Вспомогательную секущую плоскость рекомендуется выбирать таким образом, чтобы она пересекала поверхность по простым линиям (прямым или окружностям). Кроме того, проекции линий пересечения также должны быть или прямыми, или окружностями. Указанный способ построения называется способом вспомогательных секущих плоскостей. Это тот же способ, который применяется и при пересечении плоских фигур.

Рассмотрим примеры построения линии пересечения поверхностей плоскостью.

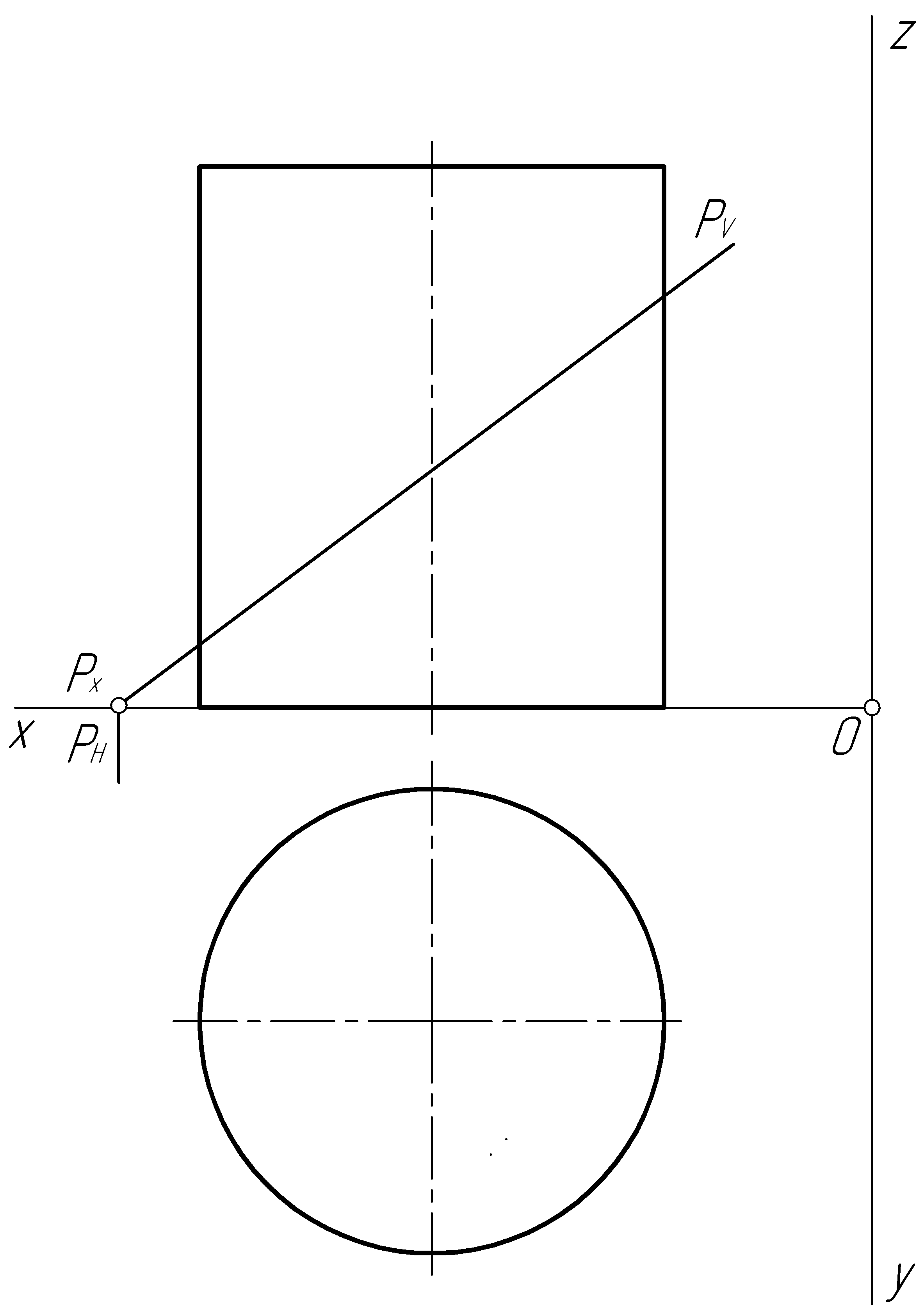
Пример 35. Построить проекции линии пересечения прямого кругового цилиндра фронтально-проецирующей плоскостью Р (рис. 92, а).

Решение. Плоскость Р (P_V) пересекает цилиндр по эллипсу. Фронтальная проекция линии пересечения представляет собой отрезок прямой, совпадающий со следом плоскости P_V . Горизонтальная проекция – окружность, совпадающая с очерком цилиндра на горизонтальной плоскости проекций. Профильную проекцию строим, используя профильные проекции точек линии сечения (рис. 92, б).

а)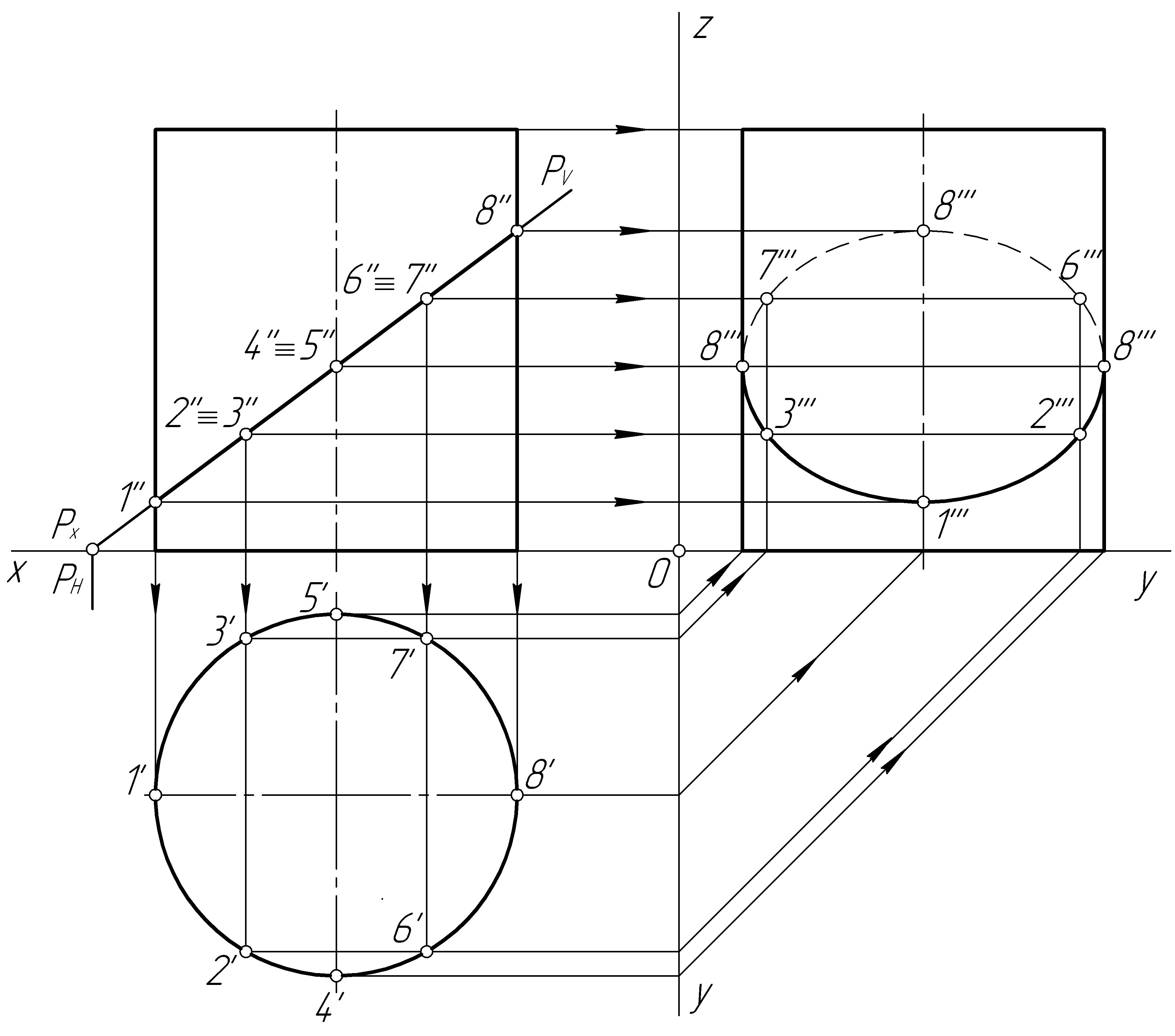

б)

Рис. 92

При сечении конической поверхности плоскостью возникают следующие виды сечений: эллипс, парабола, гипербола, окружность, две пересекающиеся прямые и точки.

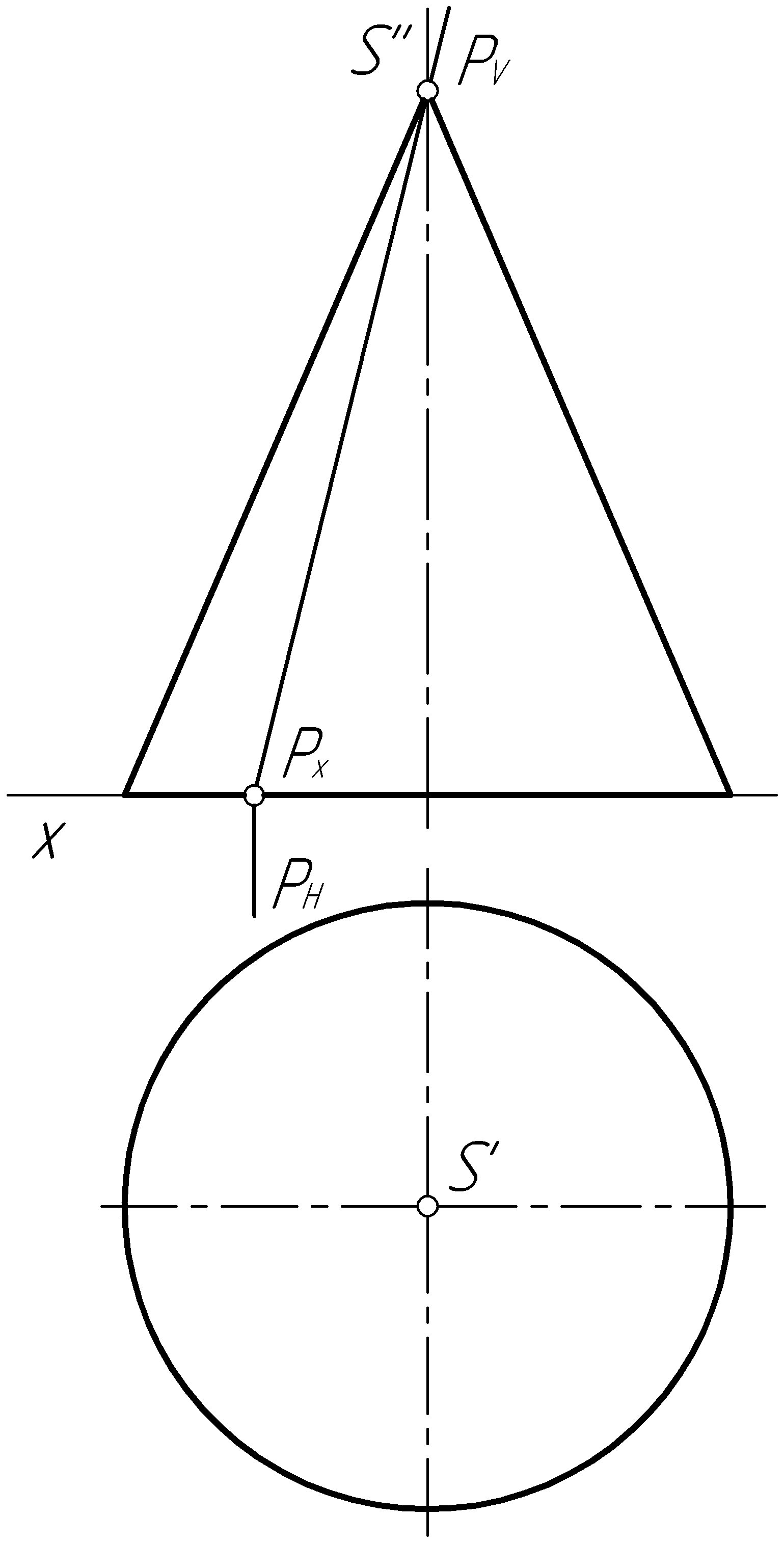
Пример 36. Построить проекции линии пересечения прямого кругового конуса фронтально-проецирующей плоскостью Р (рис. 93, а).

Решение. Плоскость Р проходит через вершину конуса S и пересекает конус по образующим S1 (S'1', S''1'') и S2 (S'2', S''2'') (рис. 93, б).

а)	б)

Рис. 93

Пример 37. Построить проекции линии пересечения прямого кругового конуса плоскостью Р (рис. 94, а).

Решение. Плоскость Р (P_V) параллельна круговому основанию конуса и пересекает его по окружности радиусом R (рис. 94, б).

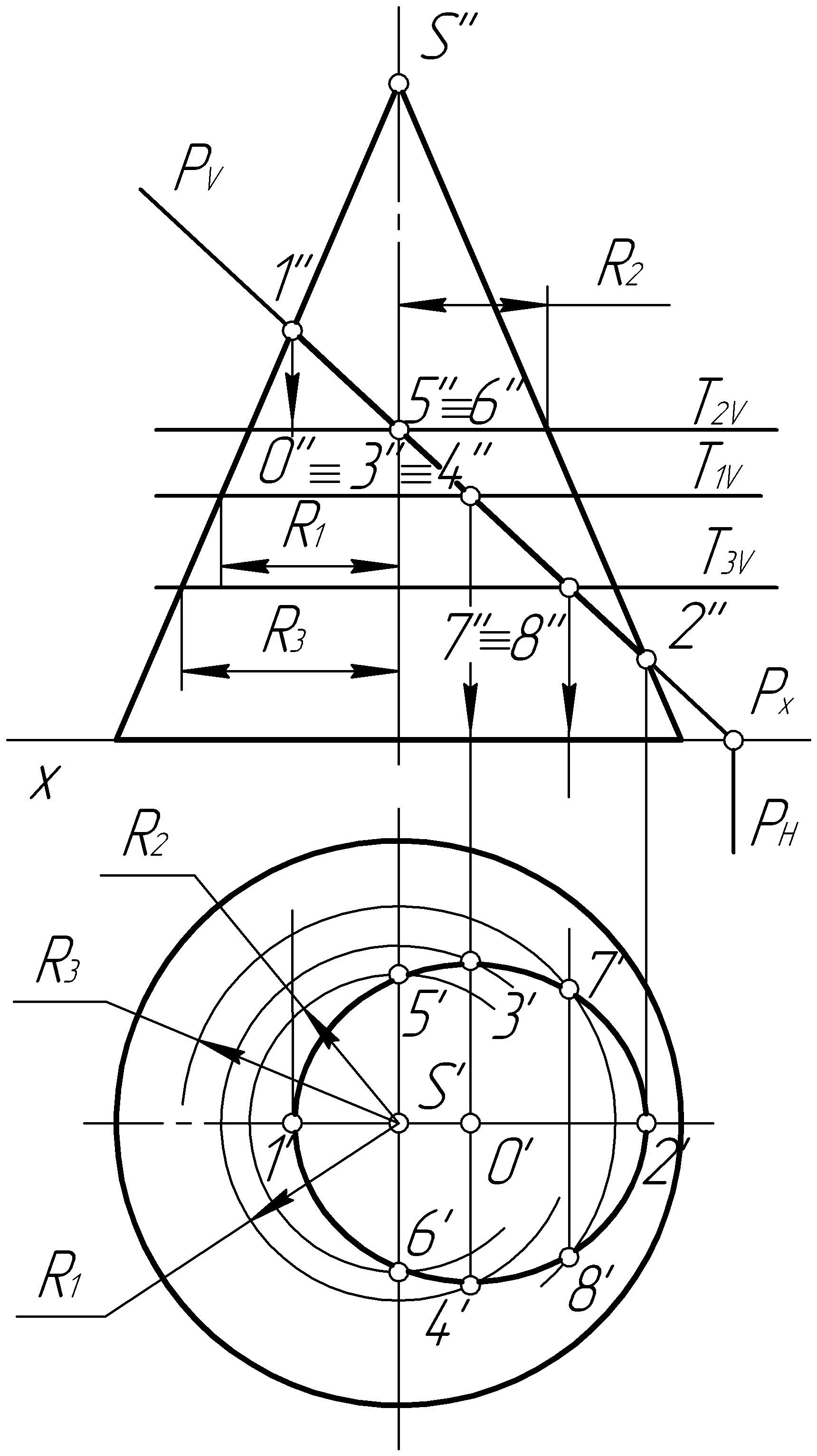
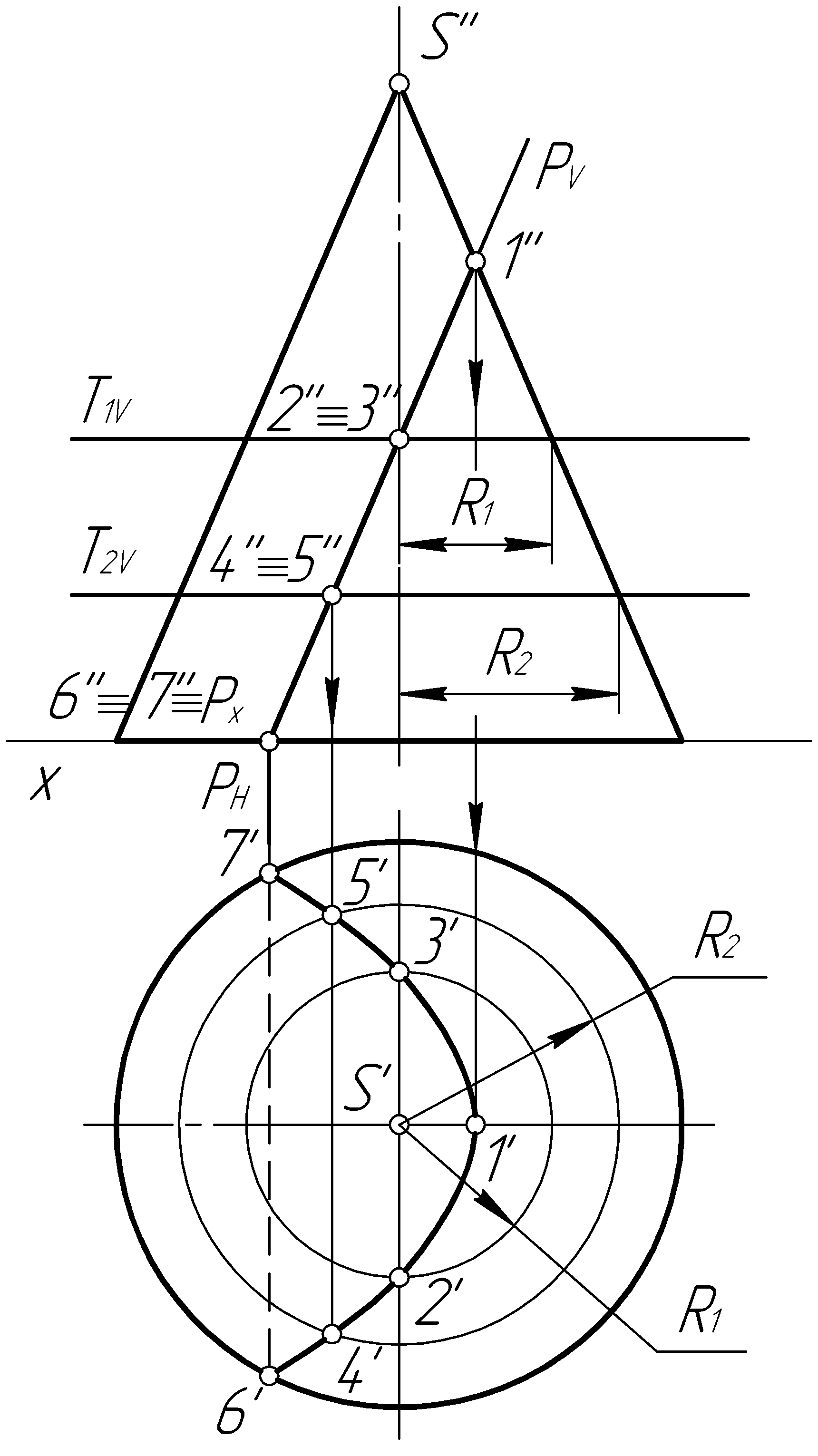
Пример 38. Построить проекции линии пересечения прямого кругового конуса фронтально-проецирующей плоскостью Р (рис. 95, а).

Решение. Плоскость Р (P_V) пересекает конус по эллипсу. Фронтальная проекция эллипса представляет собой отрезок прямой, совпадающий со сле-

а)	б)

Рис. 94

а)	б)

Рис. 95

дом P_V. Для построения горизонтальной проекции находим точки, определяющие большую ось эллипса – это точки 1 (1', 1'') и 2 (2', 2''), лежащие на очерковых образующих конуса (рис. 95, б). Для построения малой оси эллипса делим отрезок 12 (1'2', 1''2'') пополам и определяем центр эллипса – точку О (О', О''). Затем через центр О (О', О'') проводим вспомогательную плоскость Т₁ (Т_1V) и строим окружность радиусом R₁, на которой находим точки 3 (3', 3'') и 4 (4', 4''). Отрезок 34 (3'4', 3''4'') – малая ось эллипса. Дополнительные точки строим при помощи вспомогательных секущих плоскостей Т₂ (Т_2V) и Т₃ (Т_3V). Плавной линией соединяем построенные точки.

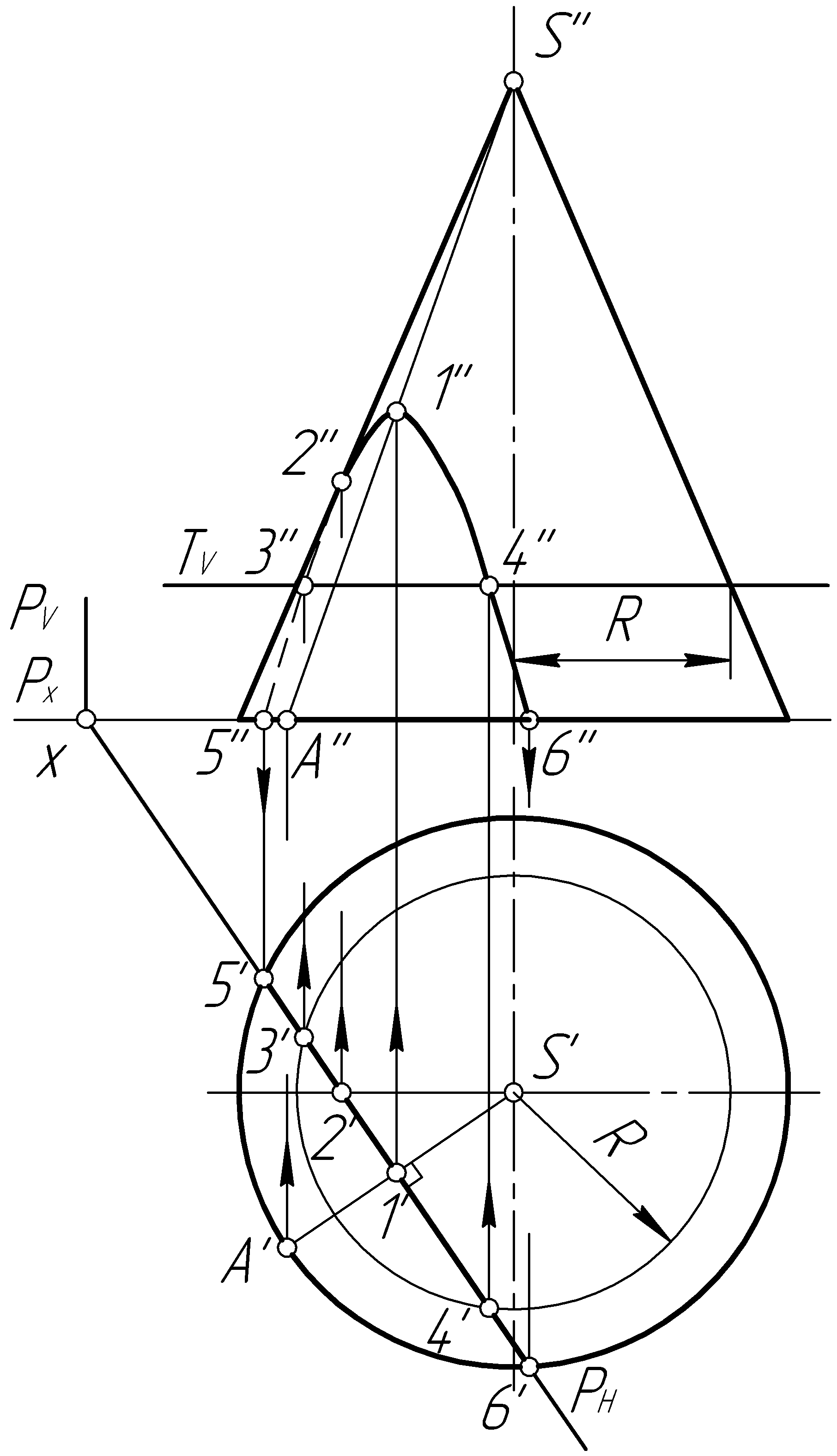
Пример 39. Построить проекции линии пересечения прямого кругового конуса фронтально-проецирующей плоскостью Р (рис. 96, а).

а)	б)

Рис. 96

Решение. Плоскость Р (P_V) параллельна одной из образующих конуса и пересекает его по параболе. Фронтальная проекция параболы представляет отрезок прямой, совпадающий со следом P_V. Для построения горизонтальной проекции определим вершину 1 (1', 1'') – она находится на очерковой образующей конуса (рис. 96, б). Дополнительные точки, определяющие построение кривой, построим при помощи вспомогательных горизонтальных плоскостей Т₁ (Т_1V) и Т₂ (Т_2V), которые пересекают конус по окружностям радиусов R₁ и R₂. На пересечении этих окружностей с плоскостью Р, находятся дополнительные точки 2 (2', 2''), 3 (3', 3''), 4 (4', 4'') и 5 (5', 5''). Крайние точки 6 (6', 6'') и 7 (7', 7'') получаем при пересечении следа P_V с основанием конуса. Плавной линией соединяем полученные точки и получаем горизонтальную проекцию параболы.

Пример 40. Построить проекции линии пересечения прямого кругового конуса горизонтально-проецирующей плоскостью Р (рис. 97, а).

а)	б)

Рис. 97

Решение. Плоскость Р (P_Н) параллельна двум образующим конуса и пересекает его по гиперболе. Горизонтальная проекция гиперболы представляет собой отрезок прямой, совпадающий со следом P_Н. Для построения вершины гиперболы проведем образующую SA (S'A', S''A''), перпендикулярную следу P_Н (рис. 97, б). При пересечении образующей SA (S'A', S''A'') и следа P_Н находим точку 1 (1', 1''), которая является вершиной гиперболы. Для построения видимости фронтальной проекции линии сечения определим точку пересечения крайней образующей конуса со следом P_Н – это точка 2 (2', 2''). Эта точка будет граничной при определении видимости. Дополнительные точки 3 (3', 3'') и 4 (4', 4'') построены при помощи вспомогательной горизонтальной секущей плоскости Т (Т_V). Крайние точки 5 (5', 5'') и 6 (6', 6'') определены как точки пересечения следа P_Н с основанием конуса.

Плавной линией соединяем полученные точки и получаем фронтальную проекцию гиперболы.

Пример 41. Построить проекции линии пересечения прямого кругового конуса плоскостью Р общего положения (рис. 98, а).

а)

Рис. 98

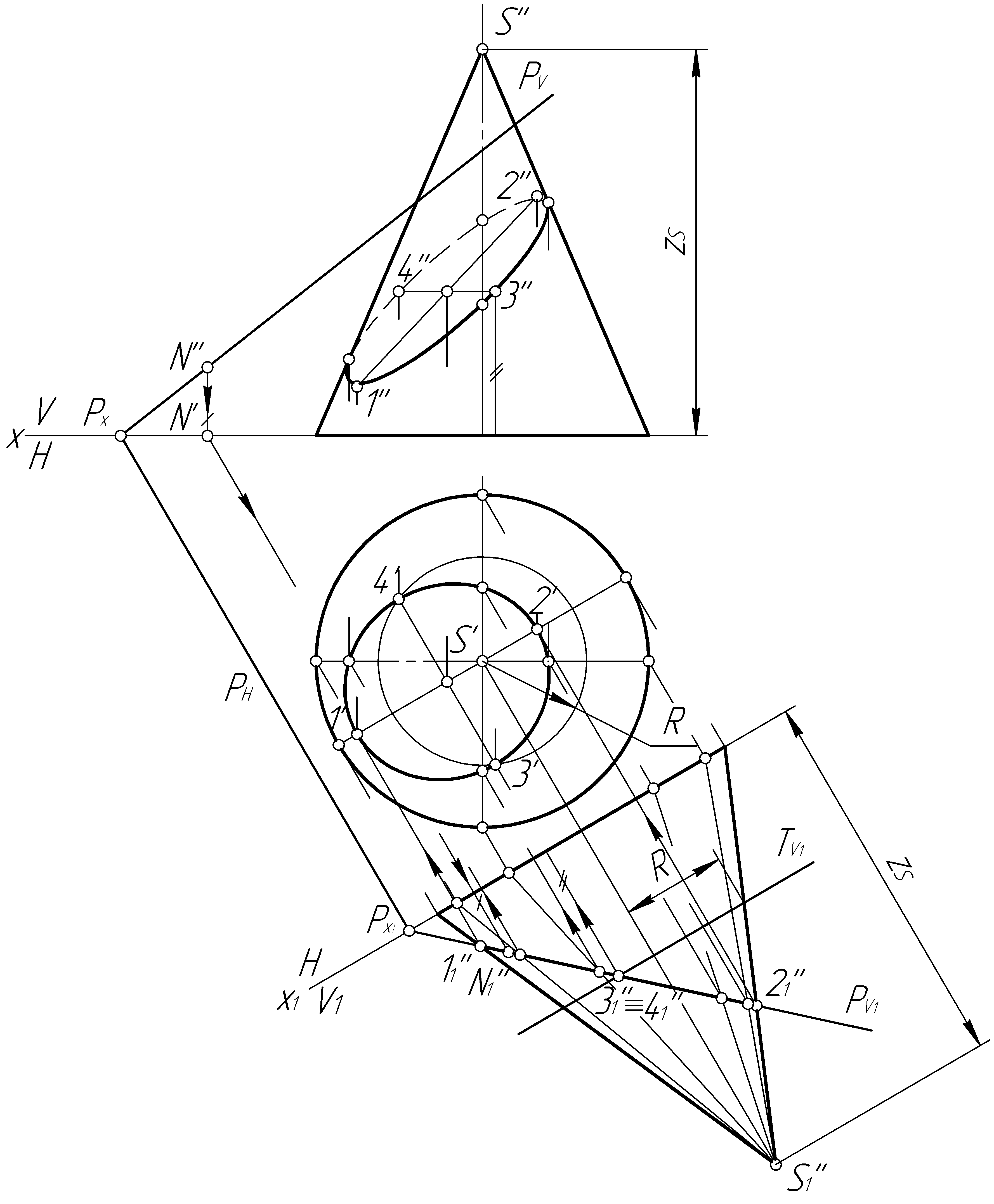
б)

Рис. 98. Продолжение

Решение. Плоскость Р (P_Н, P_V) пересекает конус по эллипсу. Воспользуемся способом перемены плоскостей проекций, и преобразуем систему плоскостей проекций так, чтобы плоскость сечения стала проецирующей. Для этого введем плоскость V₁, перпендикулярную Р (рис. 98, б). Ось х₁  проведем перпендикулярно следу P_Н , и построим фронтальную проекцию конуса. Дальнейшие построения аналогичны рассмотренным в примере 38.

Пример 42. Построить проекции линии пересечения пирамиды SABCD фронтально-проецирующей плоскостью Р (рис. 99, а).

Решение. Так как плоскость Р (P_V) – фронтально-проецирующая, то фронтальная проекция линии пересечения представляет собой отрезок прямой, совмещенный со следом P_V плоскости. Обозначим точки пересечения ребер пирамиды SA, SB, SC и SD со следом P_V соответственно 1'', 2'', 3'', 4'', и построим их горизонтальные и профильные проекции (рис. 99, б). Горизонтальные проекции 2' и 4' точек 2 и 4 построим, используя их профильные проекции (по условию задачи ребра SB (S'В', S''В'') и SD (S'D', S''D'') – профильные прямые).

Видимость ребер на проекциях определяем следующим образом: на фронтальную проекцию смотрим по направлению s'. Видимыми будут ребра SA (S''А''), SB (S''В'') и SC (S''С''). На горизонтальной проекции направление взгляда совпадает с направлением s'', тогда видимыми будут все ребра. На профильную проекцию смотрим по направлению s''' и видимыми будут ребра SA (S'''А'''), SB (S'''В''') и SD (S'''D''').

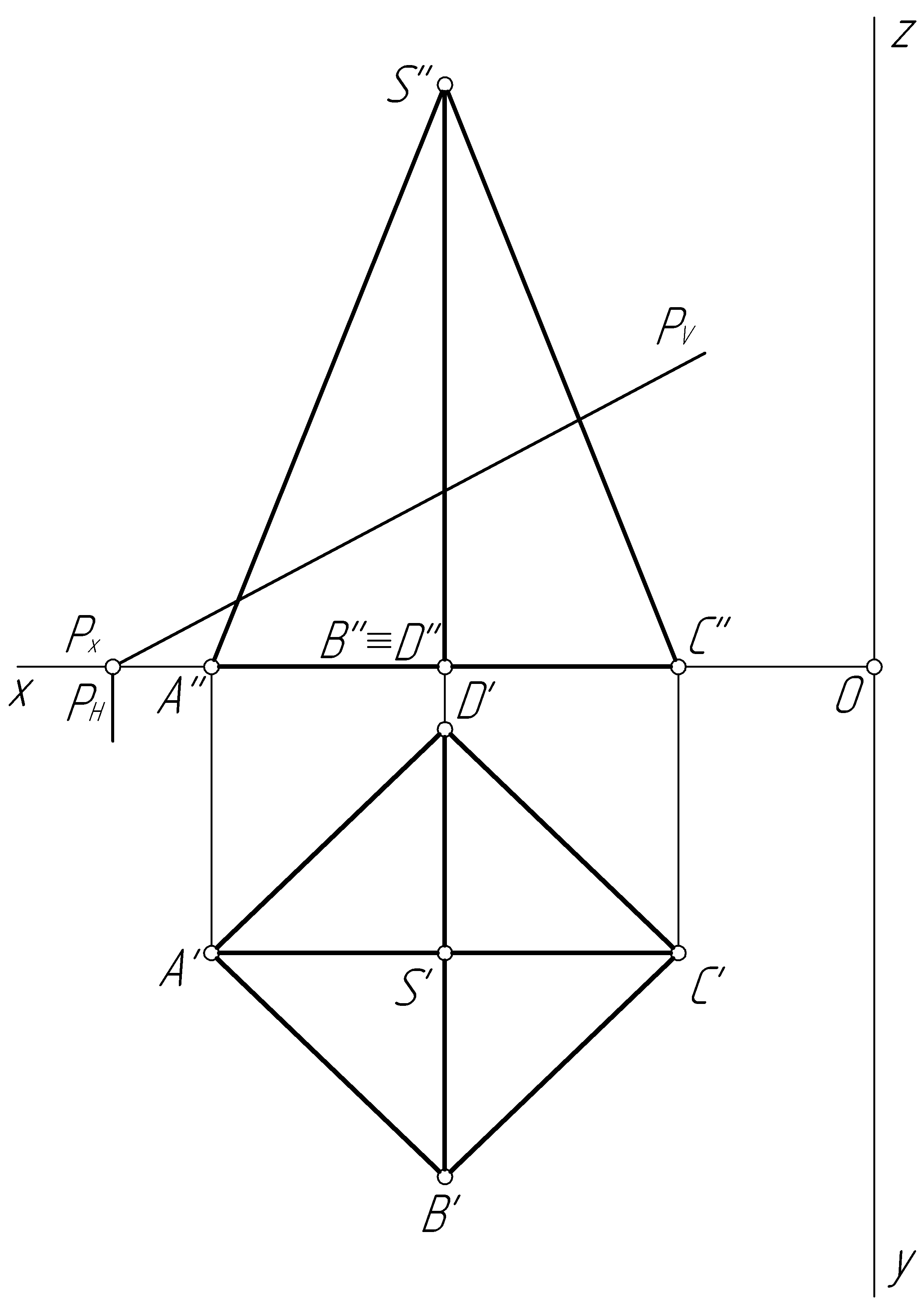
а)

Рис. 99

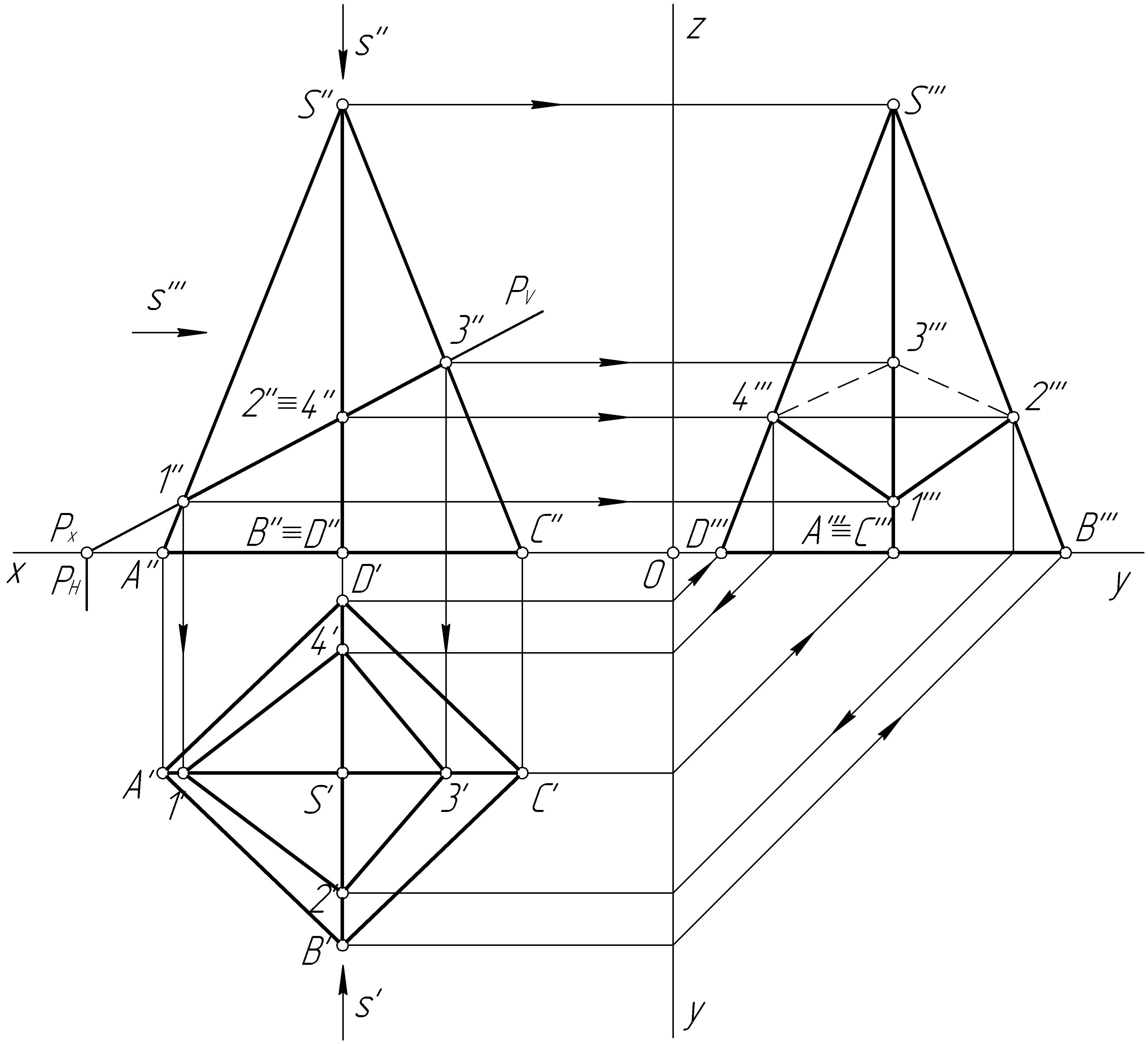
б)

Рис. 99. Продолжение

Соединяем полученные проекции точек, и строим проекции линии пересечения.

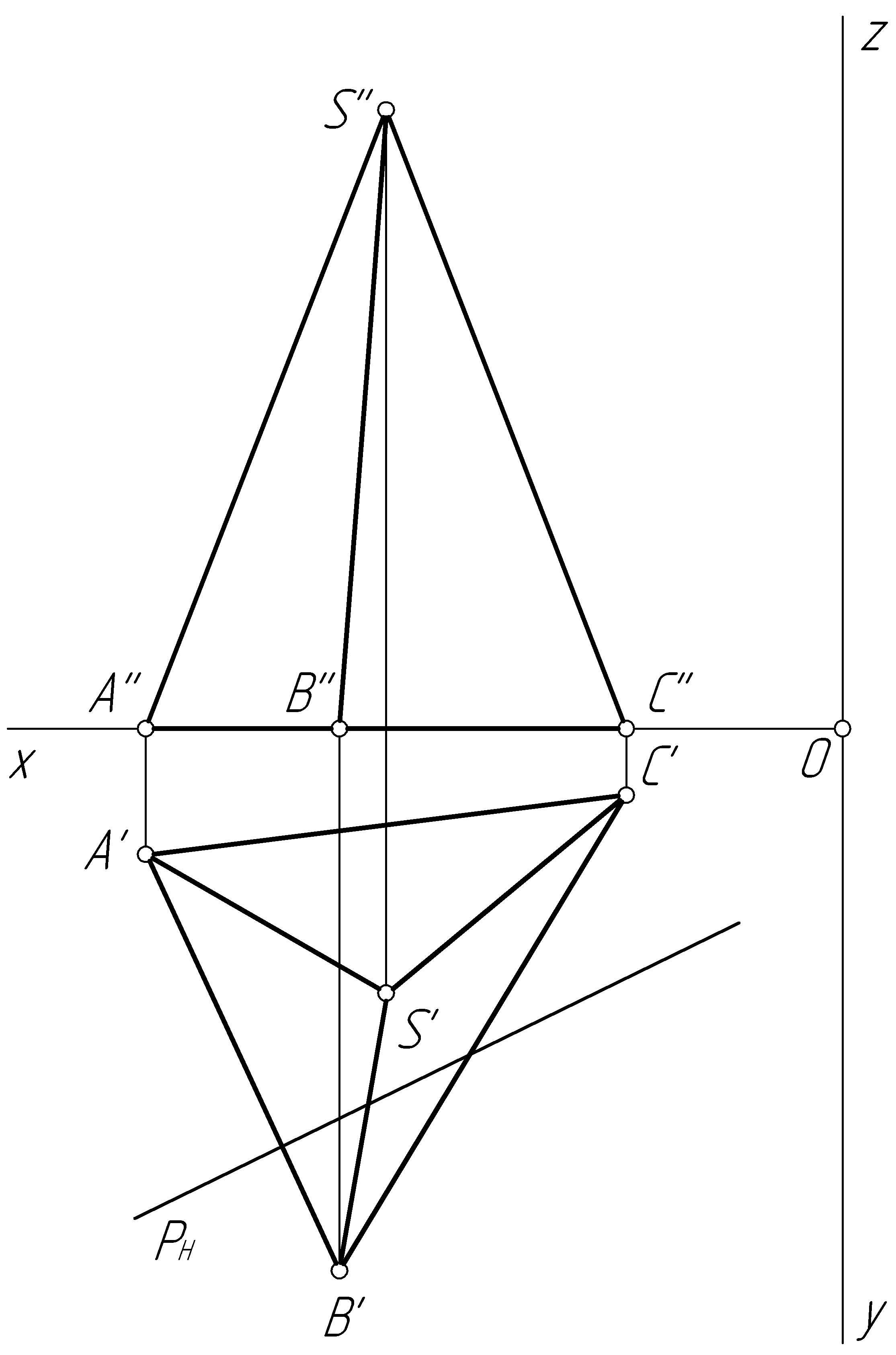
Пример 43. Построить проекции линии пересечения пирамиды SABC горизонтально-проецирующей плоскостью Р (рис. 100, а).

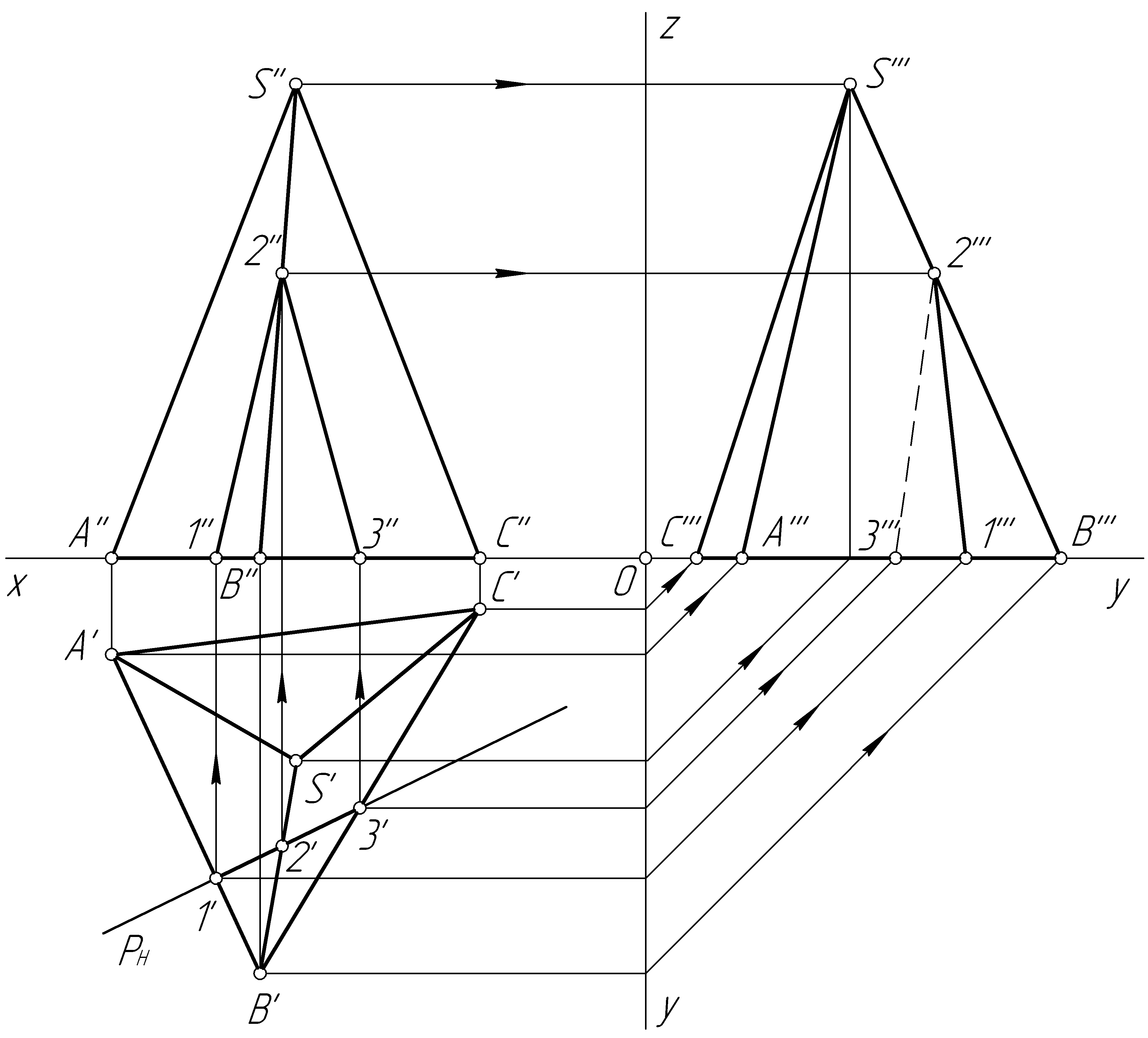
Решение. По условию задачи плоскость Р (P_Н) – горизонтально-проецирующая. Поэтому горизонтальная проекция линии сечения представляет собой отрезок прямой, совмещенный со следом P_Н. Обозначим точки пересечения следа P_Н плоскости с ребрами пирамиды 1', 2', 3', и построим фронтальные и профильные проекции точек пересечения (рис. 100, б). Соединяем проекции точек пересечения между собой и получаем проекции линии пересечения. Затем определяем видимость отрезков.

а)

б)

Рис. 100

а)

б)

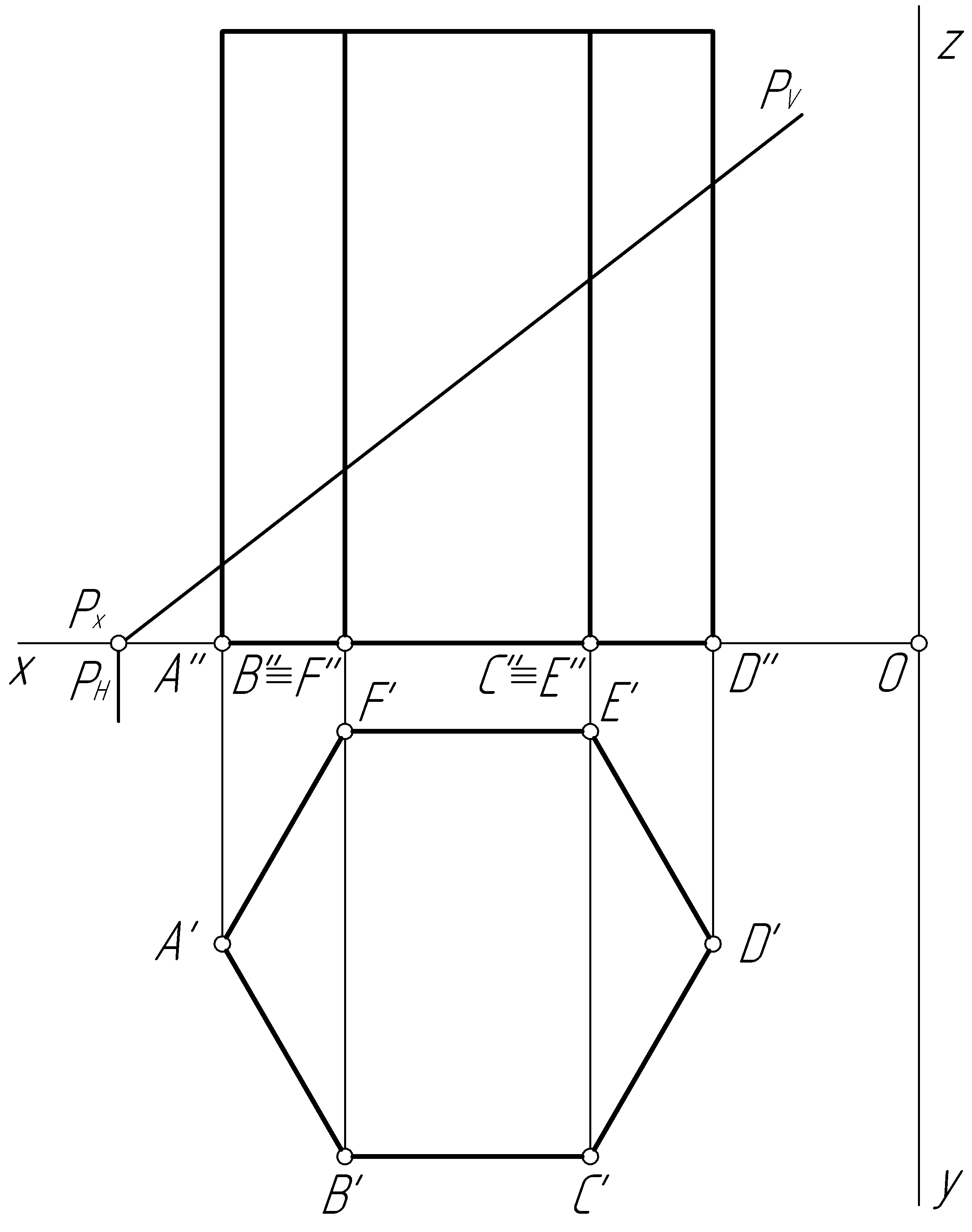
Рис. 101

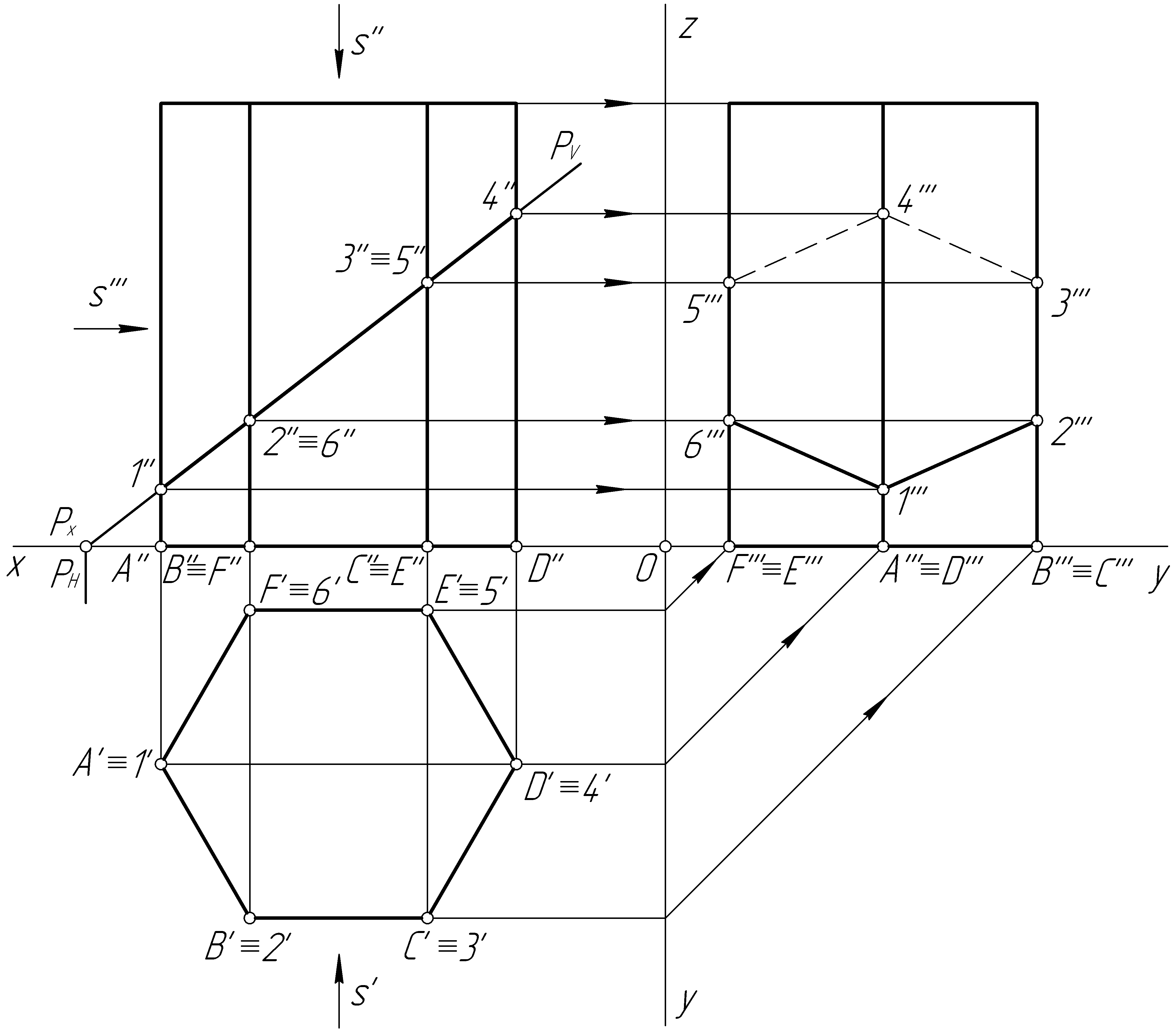
Пример 44. Построить проекции линии пересечения прямой призмы фронтально-проецирующей плоскостью Р (рис. 101, а).

Решение. Плоскость Р (Р_V) – фронтально-проецирующая и пересекает ребра призмы в точках 1 – 6 (рис. 101, б). Фронтальные проекции точек 1'', 2'', 3'', 4'', 5'', 6'' совпадают со следом Р_V и представляют собой отрезок прямой. Горизонтальные проекции точек 1', 2', 3', 4', 5', 6' совпадают с горизонтальными проекциями ребер призмы (так как по условию задачи призма прямая и стоит на плоскости проекций Н). Строим профильные проекции точек, соединяем их отрезками прямых и определяем видимость.

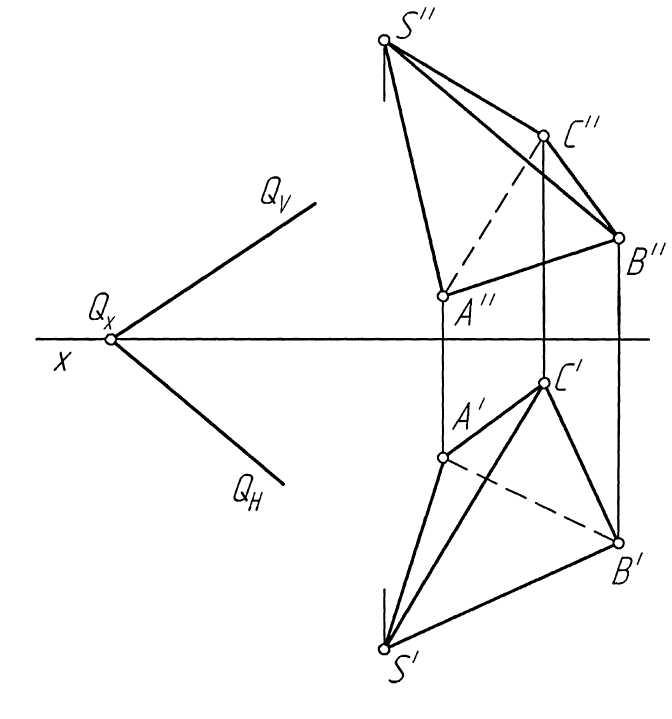
Пример 45. Построить проекции линии пересечения пирамиды SABC плоскостью Q общего положения (рис. 102, а).

Решение. Для решения задачи (рис. 102, б) удобно применять способ перемены плоскостей проекций. Преобразуем систему плоскостей проекций таким образом, чтобы плоскость Q в этой системе стала горизонтально-проецирующей. Для этого проводим горизонтальную плоскость проекций H₁, перпендикулярную плоскости Q. Тогда новая ось проекций будет перпендикулярна следу

а)

Рис. 102

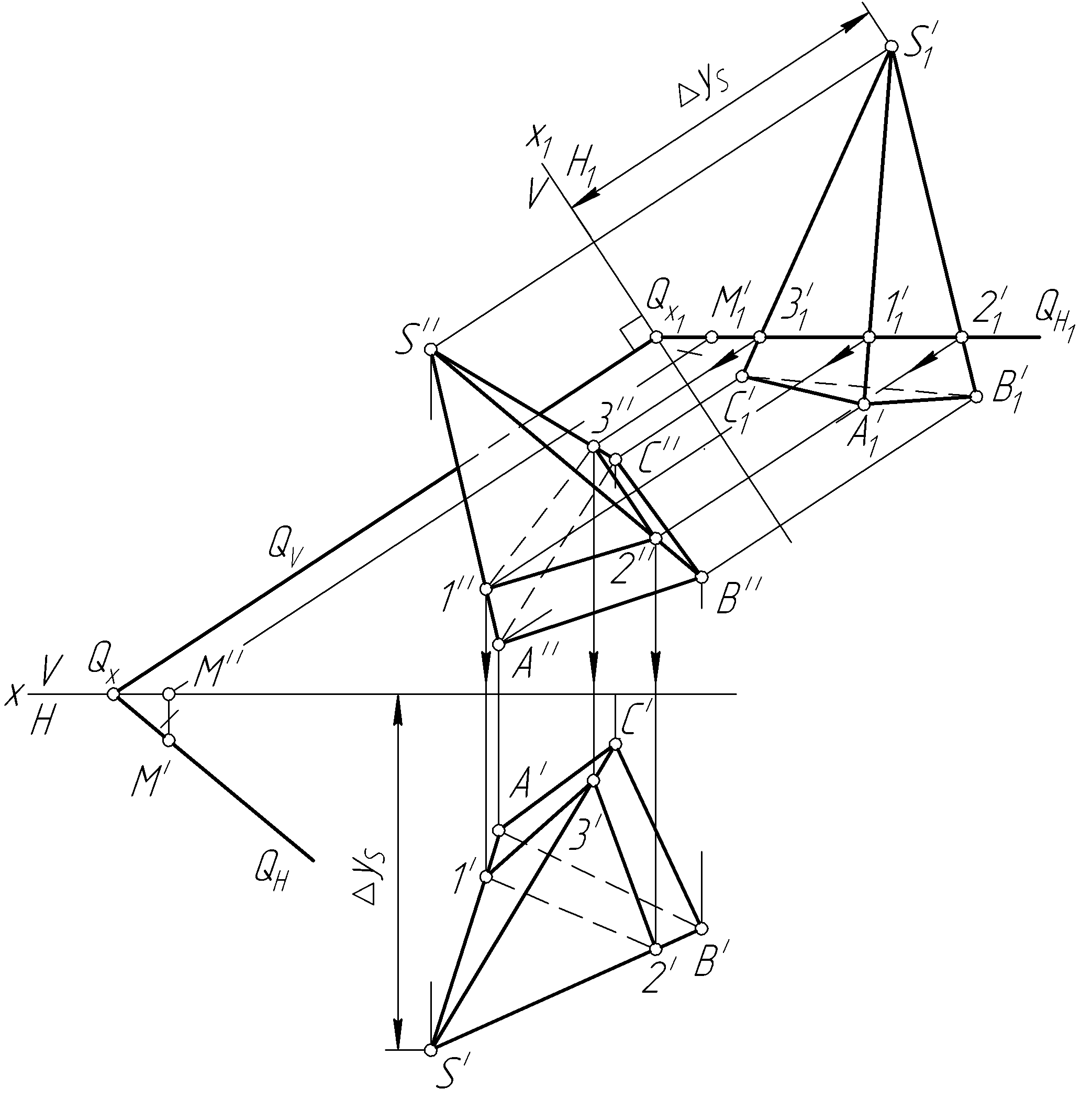
б)

Рис. 102. Продолжение

плоскости Q. В новой системе плоскостей проекций строим горизонтальный следплоскостии новую горизонтальную проекциюпирамиды. Определяем точки пересечения горизонтального следаплоскостиQ с ребрами пирамиды. Прямая – горизонтальная проекция линии сечения в системе плоскостей проекций. Проецируем точки сечения на ребра пирамиды в систему, и получаем проекции,,и,,вершин фигуры сечения. Соединяем последовательно одноименные проекции точек1 (,),2 (,) и3 (,), и получаем проекции фигуры сечения пирамиды плоскостью.

Развертывание многогранников. Развертыванием поверхности называется процесс ее совмещения с некоторой плоскостью. Поверхность, которая может быть совмещена с плоскостью без разрывов и складок, называется развертываемой, а полученное при этом изображение – ее разверткой. Многогранные поверхности являются развертываемыми.

Развертка многогранника (многогранной поверхности) представляет собой плоскую фигуру, состоящую из совокупности всех его граней. Рассмотрим построение разверток пирамид и призм как наиболее распространенных в инженерной практике.

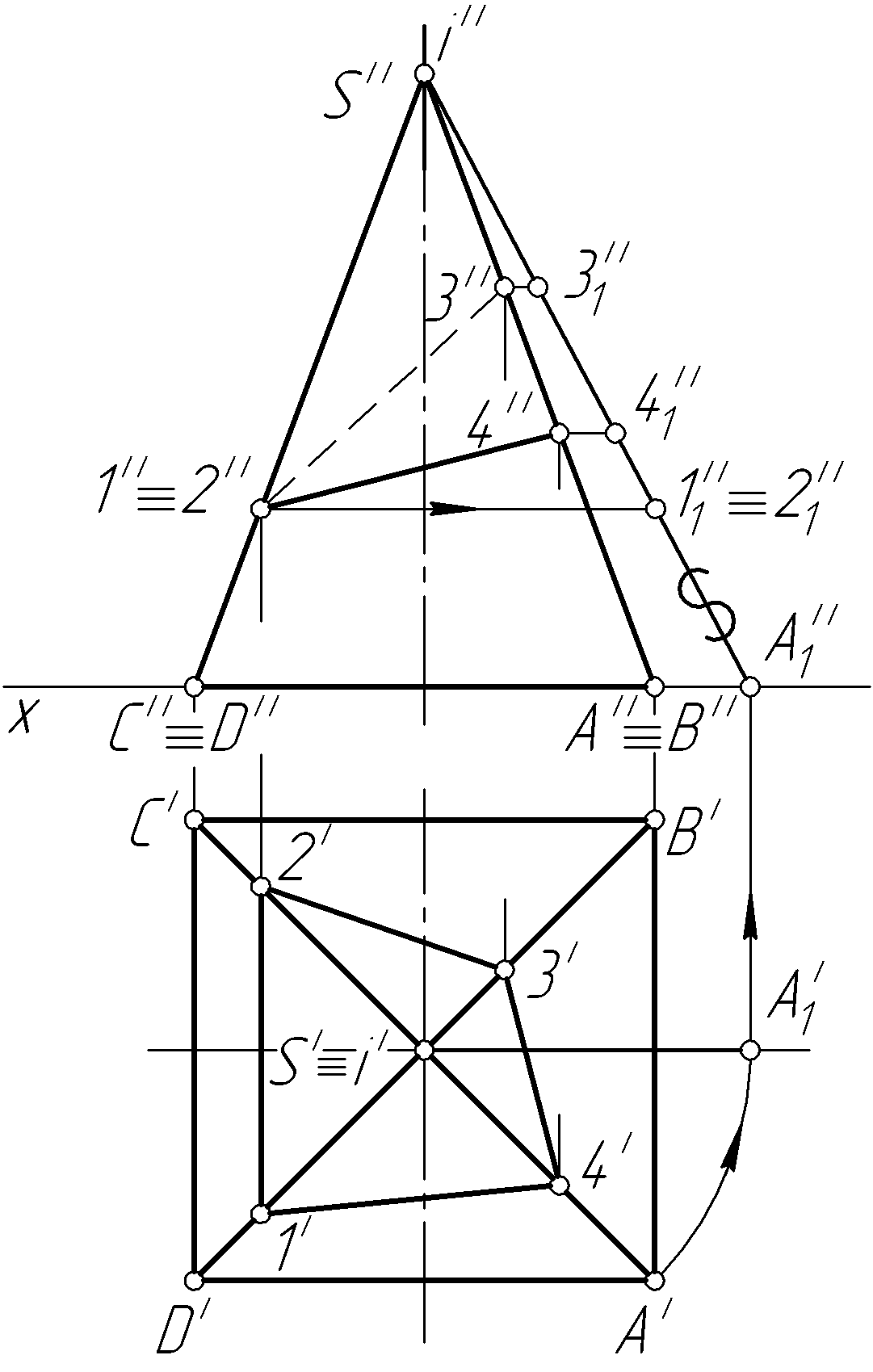
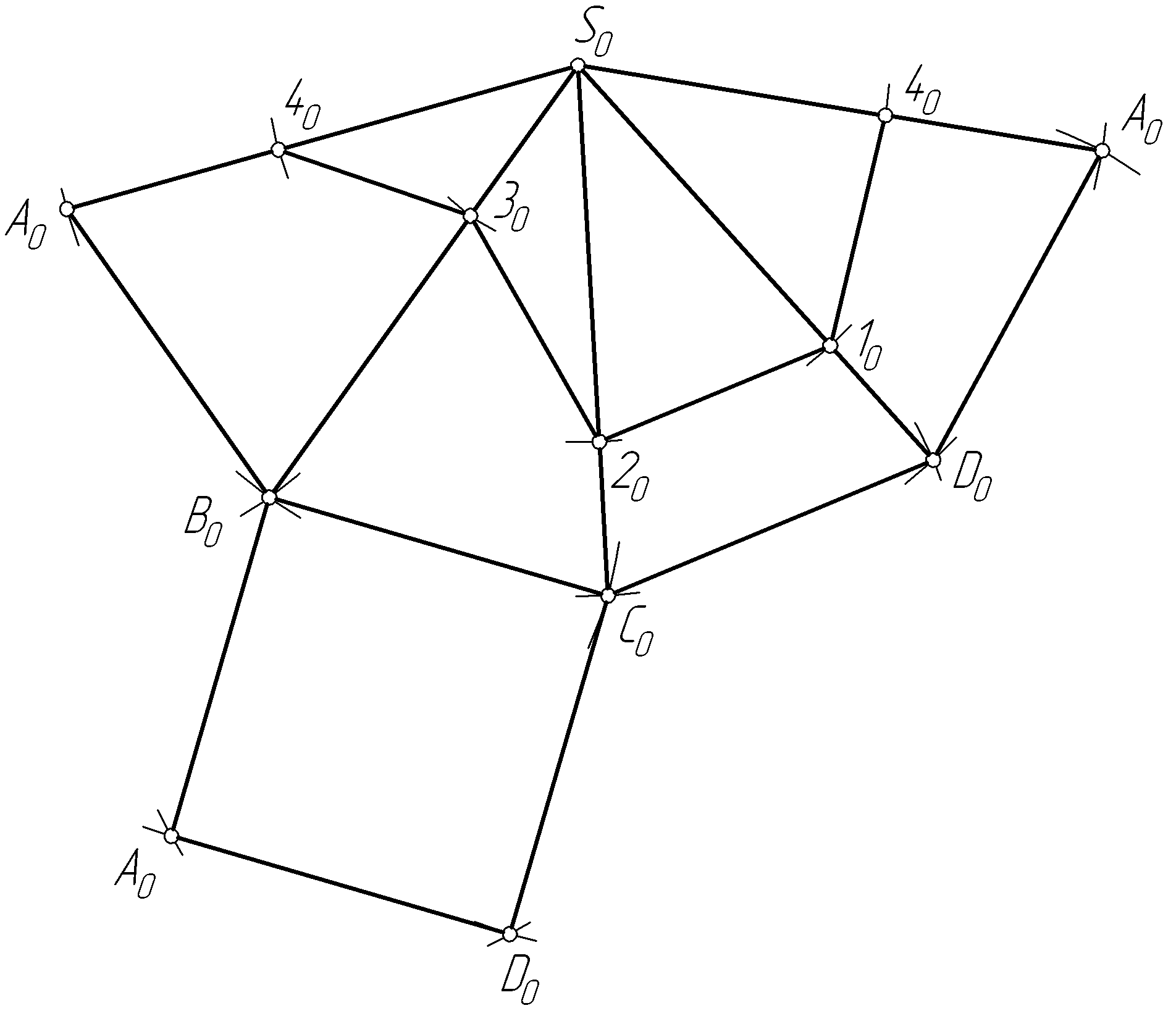
Пример 46. Построить полную развертку правильной четырехугольной пирамиды и нанести на нее ломаную линию 12341, принадлежащую поверхности пирамиды (рис. 103, а).

Решение. Развертка полной поверхности пирамиды представляет собой совокупность ее основания (в данном случае квадрат) и всех граней (треугольников).

Для построения развертки боковой поверхности заданной пирамиды вначале необходимо определить натуральную величину всех ее ребер SА (S'A', S''A''), SВ (S'В', S''В''), SС (S'C', S''C''), SD (S'D', S''D''). Натуральную величину ребер удобно определить их вращением вокруг горизонтально-проецирующей оси i (i', i''), совпадающей с высотой пирамиды (см. пример 23). Поскольку заданная пирамида правильная и все ее боковые ребра равны между собой, то достаточно найти натуральную величину одного из них, например, SА (S'A', S''A'') (рис. 103, б).

Основание пирамиды расположено в горизонтальной плоскости проекций, поэтому на эту плоскость оно проецируется без искажения (A'B'C'D'

ABCD). Если основание пирамиды расположено в пространстве произвольно относительно плоскостей проекций (не параллельно и не принадлежит ни одной из плоскостей проекций), то для построения развертки такой пирамиды необходимо дополнительно определить натуральную величину ребер основания (или, что то же самое, плоской фигуры основания) любым способом преобразования проекций.

На рис. 103, в показана полная развертка пирамиды. Боковые ее грани (треугольники S₀ A₀ B₀, S₀ В₀ С₀, S₀ С₀ D₀ и S₀ D₀ A₀) построены по трем сторонам. Так, грань S₀ A₀ B₀ строится по сторонам S₀A₀ = SA = , S₀В₀ = SB = = и А₀В₀ = AB = A'B'. Полученные таким образом точки A₀, B₀, C₀ и D₀ соединяем ломаной линией между собой и с точкой S₀. К боковым граням пирамиды на развертке пристраиваем основание, представляющее собой квадрат.

а)	б)
в)

Рис. 103

Для того чтобы нанести на развертку ломаную линию 12341, необходимо найти длины отрезков S1 (S'1', S''1''), S2 (S'2', S''2''), S3 (S'3', S''3''), S4 (S'4', S''4''), как это показано на рис. 103, б, а затем отложить их на соответствующих ребрах пирамиды на ее развертке.

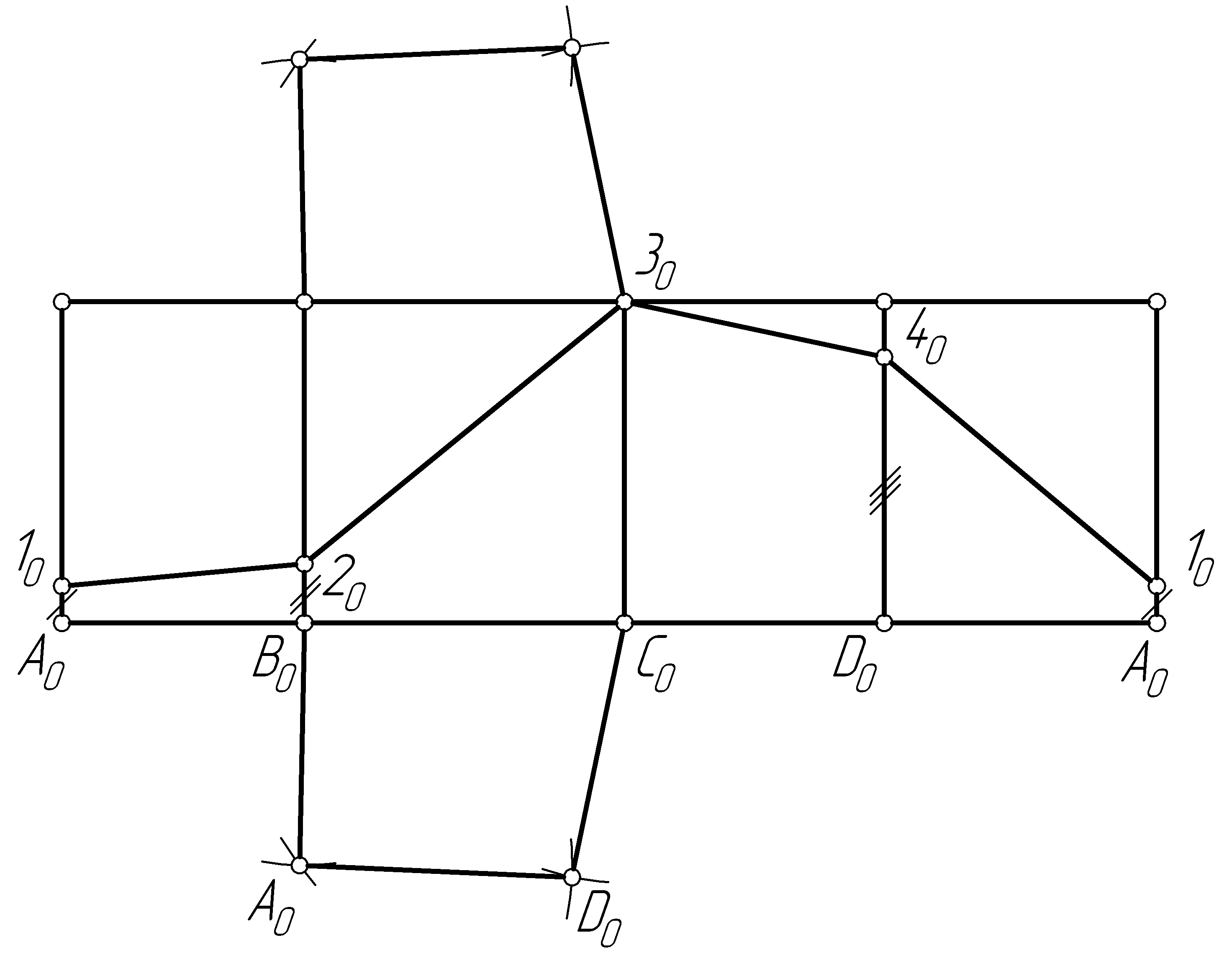
Пример 47. Построить полную развертку правильной треугольной пирамиды и нанести на нее ломаную линию 1231, принадлежащую поверхности пирамиды (рис. 104, а).

Решение. Для построения развертки пирамиды необходимо вначале определить натуральные величины ее ребер (рис. 104, б). Для этого можно применять различные способы преобразования проекций. Определим натуральную величину ребер пирамиды, например, вращением.

Ребра (,),(,) и(,), вращая вокруг оси(, ), проходящей через вершину пирамиды S (,), приводим в положение, параллельное горизонтальной плоскости проекций. Тогда горизонтальные проекции этих отрезков будут представлять натуральные величины ребер,,и соответственно отрезков,,этих ребер.

Аналогично вращая вокруг фронтально-проецирующей оси (, ), перпендикулярной фронтальной плоскости проекций и проходящей через точку С (,), реброАС (,) приводим в положение, параллельное горизонтальной плоскости проекций. Тогда горизонтальная проекция этого отрезка будет представлять собой натуральную величину ребраАС. Поскольку заданная пирамида правильная, то АС = СВ = АВ.

Далее на свободном поле чертежа, аналогично рассмотренному выше примеру 46, строим непосредственно развертку (рис. 104, в). Выбираем произвольную точку S₀ и, используя натуральную величину ребер ,,,,,, строим последовательно грани пирамиды,,, представляющие собой треугольники, по трем сторонам. Далее наносим на развертку точки1₀, 2₀ и 3₀, принадлежащие заданной ломаной линии. К любой боковой грани пирамиды, используя найденную натуральную величину одной из его сторон АС, пристраиваем основание – правильный треугольник A₀B₀C₀. В заключение последовательно соединяем между собой построенные точки ломаной линией.

а)	б)

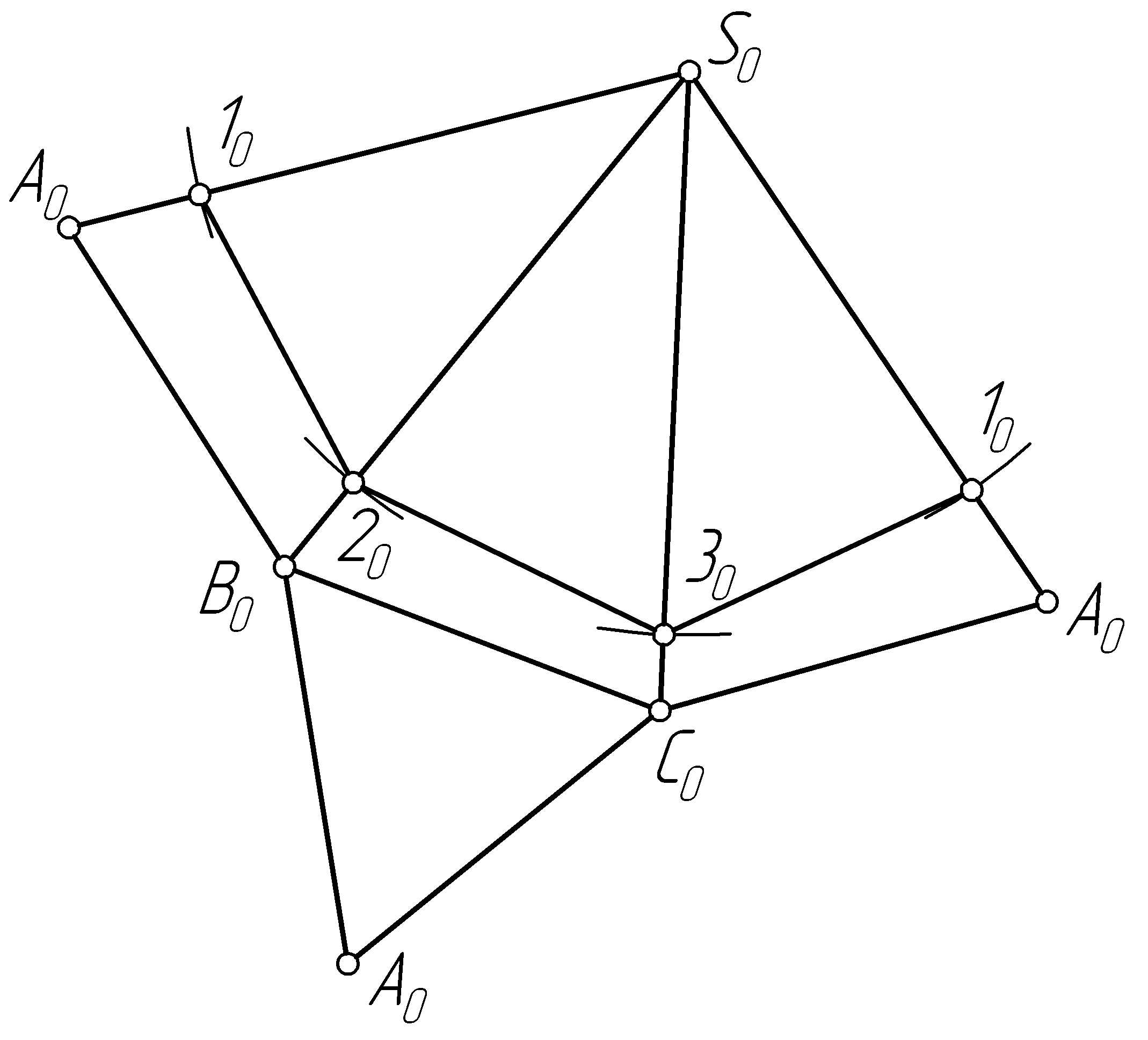
в)

Рис. 104

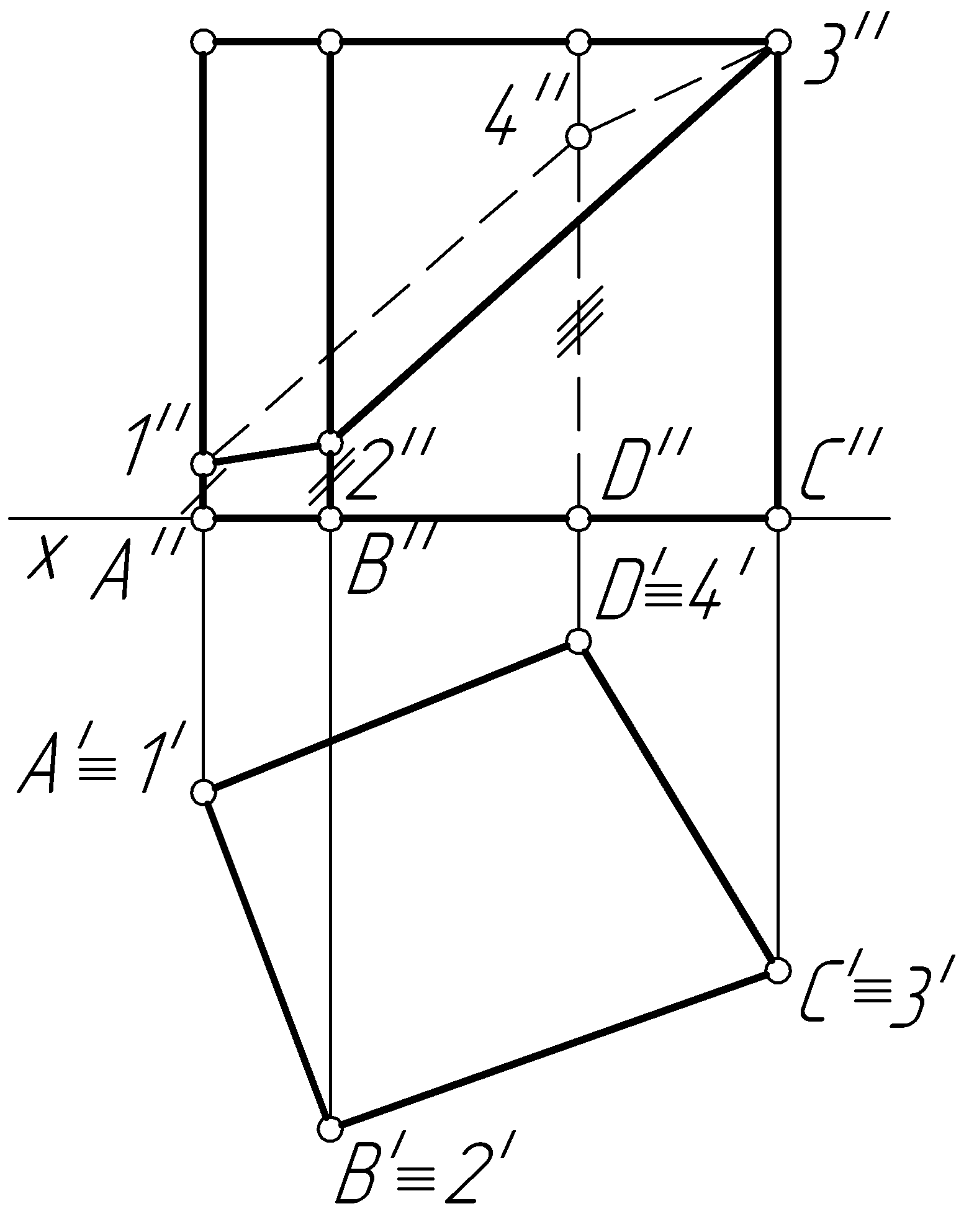
а)

б)

Рис. 105

Пример 48. Построить полную развертку четырехугольной призмы и нанести на нее ломаную линию 12341, принадлежащую поверхности призмы (рис. 105, а).

Решение. Развертка призмы представляет собой совокупность ее боковых граней (в данном случае прямоугольников) и двух равных оснований (плоских четырехугольников). Основание призмы расположено в горизонтальной плоскости проекций, поэтому на эту плоскость оно проецируется без искажения (A'B'C'D' ABCD). Боковые грани призмы представляют собой горизонтально-проецирующие плоскости, а ее ребра – горизонтально-проецирующие прямые, поэтому они проецируются на фронтальную плоскость проекций без искажения.

Для построения развертки боковой поверхности призмы откладываем на произвольной горизонтальной прямой (рис. 105, б) стороны основания А₀В₀ = АВ = A'B', В₀С₀ = ВС = В'С', C₀D₀ = CD = C'D', D₀A₀ = DA = D'A'. Из каждой точки А₀, В₀, С₀ и D₀ восстанавливаем перпендикуляр к горизонтальной прямой длиной, равной высоте призмы, и соединяем полученные точки. Пристраиваем к развертке боковой поверхности два основания призмы.

Для того чтобы нанести на развертку ломаную линию 12341, на соответствующих ребрах призмы на ее развертке откладываем отрезки А₀1₀ = А1 = A''1'', B₀2₀ = B2 = B''2'', С₀3₀ = С3 = С''3'', D₀4₀ = D4 = D''4'', как это показано на рис. 105, б, а затем откладываем их на развертке и соединяем полученные точки ломаной линией.

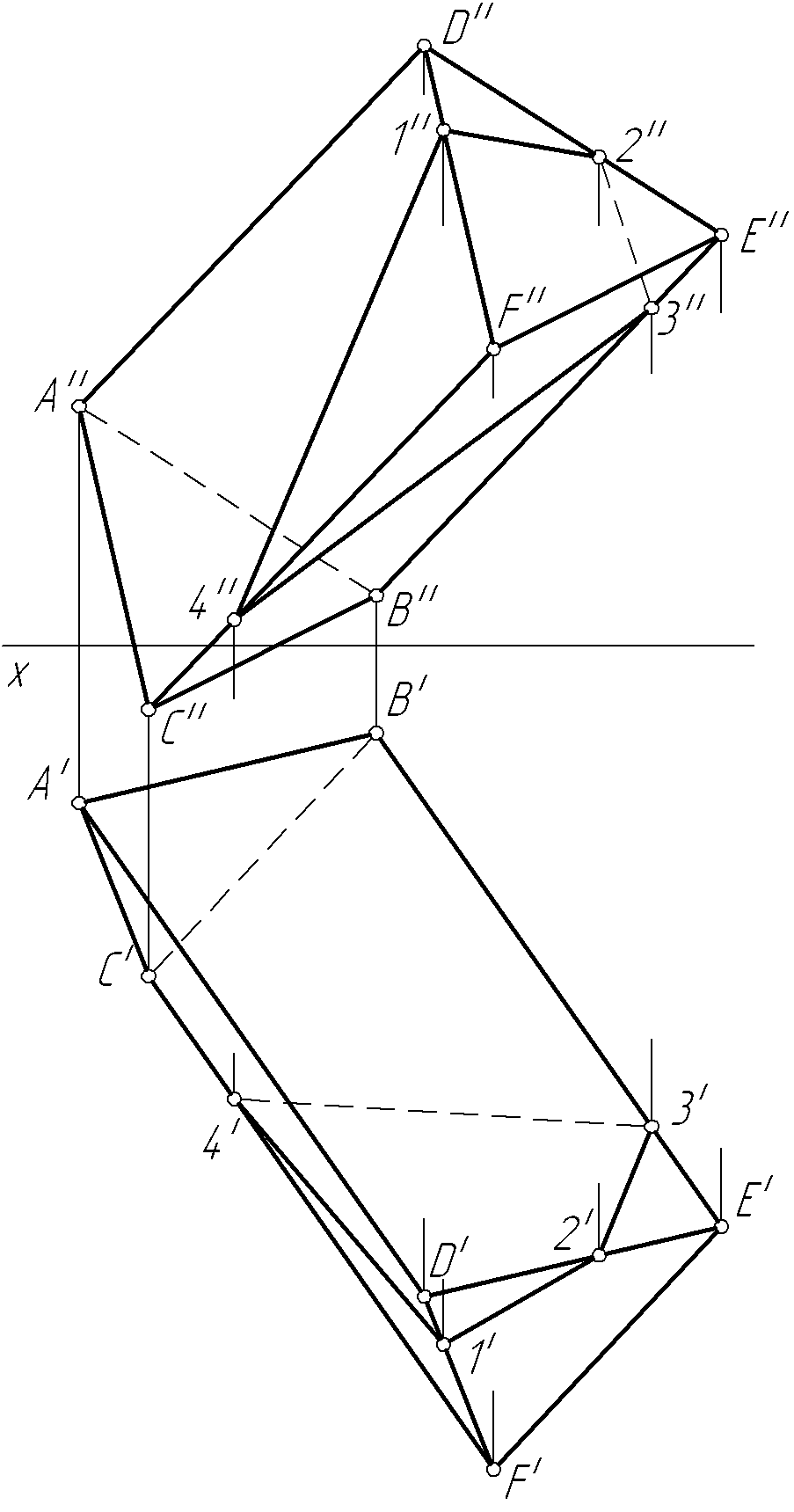
Пример 49. Построить полную развертку призмы ABCDEF и нанести на нее ломаную линию 12341, принадлежащую поверхности призмы (рис. 106, а).

Решение. Для построения развертки призмы необходимо определить натуральные величины ее ребер (рис. 106, б). Как уже отмечалось ранее, для этого можно применять различные способы преобразования проекций. Определим натуральную величину ребер призмы, например, переменой плоскостей проекций.

Введем дополнительную фронтальную плоскость проекций V₁ так, чтобы она была параллельна ребрам боковых граней призмы (рис. 106, б). В этом случае новая ось проекций будет параллельна горизонтальным проекциям этих ребер. Строим фронтальную проекцию призмы в новой системе плоскостей проекций. Проекции ребер,,определяют натуральные величины ребер боковых граней призмы.

а)

Рис. 106

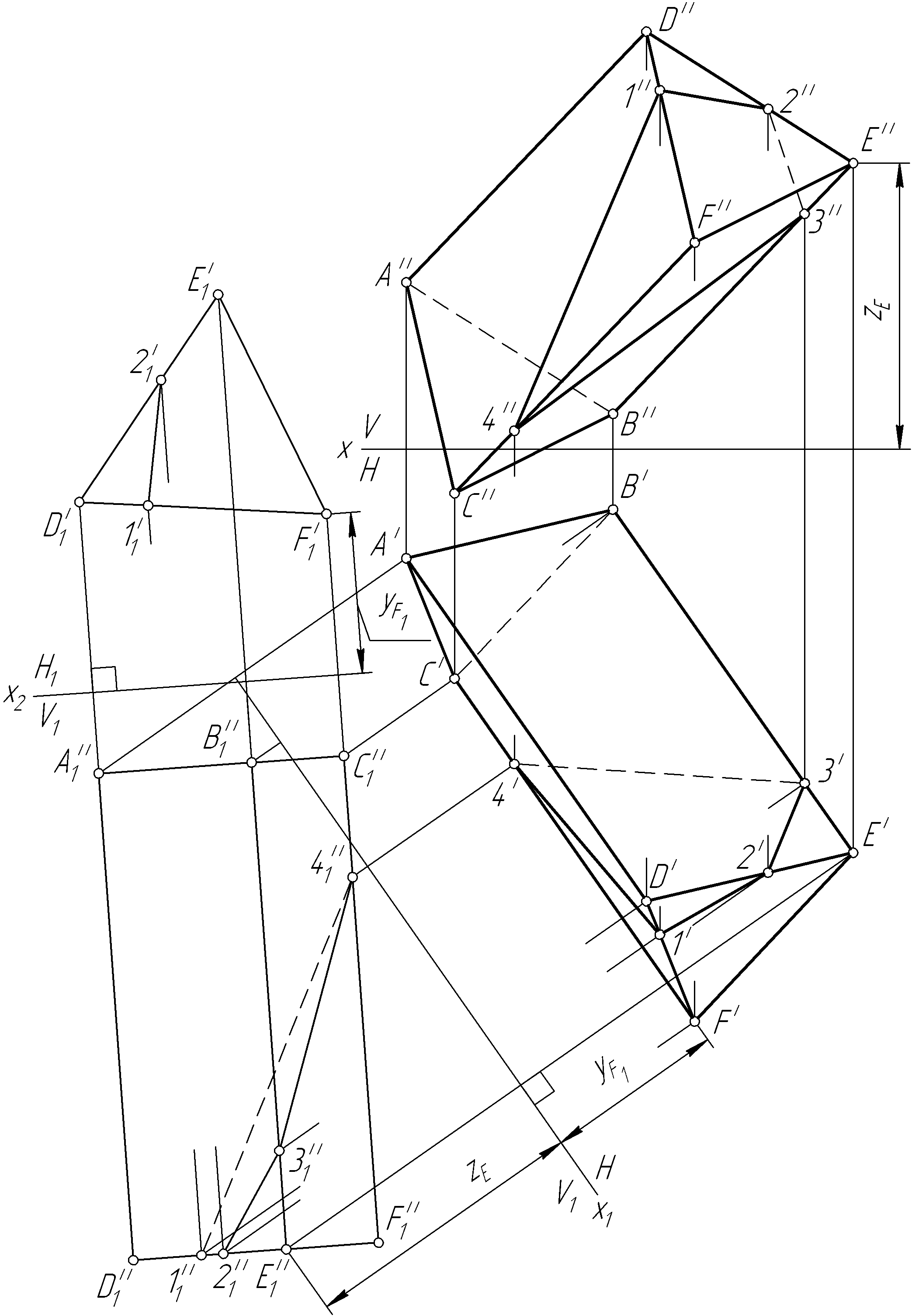
б)

Рис. 106. Продолжение

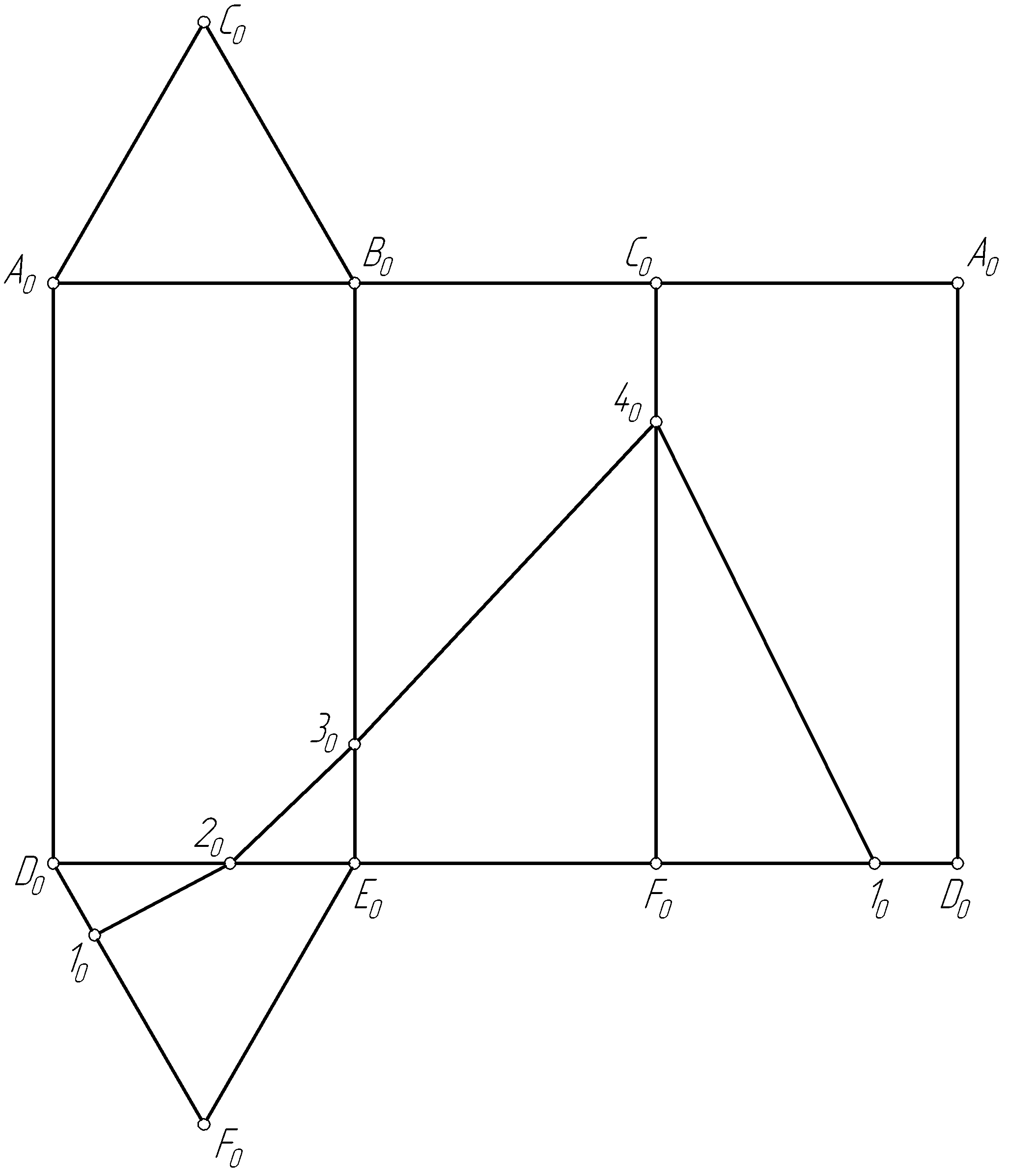
в)

Рис. 106. Окончание

Далее вводим дополнительную плоскость проекций H₁, перпендикулярную ребрам призмы и параллельную ее основаниям. Тогда новая ось будет перпендикулярна фронтальным проекциям ребер. В системеребра боковых граней призмы представляют собой горизонтально-проецирующие прямые и их проекциями на плоскостьявляются точки,и. Треугольникопределяет натуральную величину оснований призмы. Проецируем на соответствующие ребра основания точки1 и 2 и получаем натуральные величины иотрезковD1 и D2.

Далее на свободном поле чертежа, аналогично рассмотренному выше примеру, строим непосредственно развертку (рис. 106, в). Используя натуральную величину ребер AD, BE, CF, строим последовательно боковые грани А₀В₀F₀D₀, B₀C₀F₀E₀ и C₀A₀D₀F₀ призмы, представляющие собой прямоугольники, и к любой грани пристраиваем основания – треугольники A₀B₀C₀ и D₀E₀F₀, используя найденные натуральные величины ребер AB, BC, CA, DE, EF и FD. Затем наносим на развертку точки 1₀, 2₀, 3₀ и 4₀, принадлежащие заданной ломаной линии. В заключение последовательно соединяем между собой ломаной линией построенные точки.

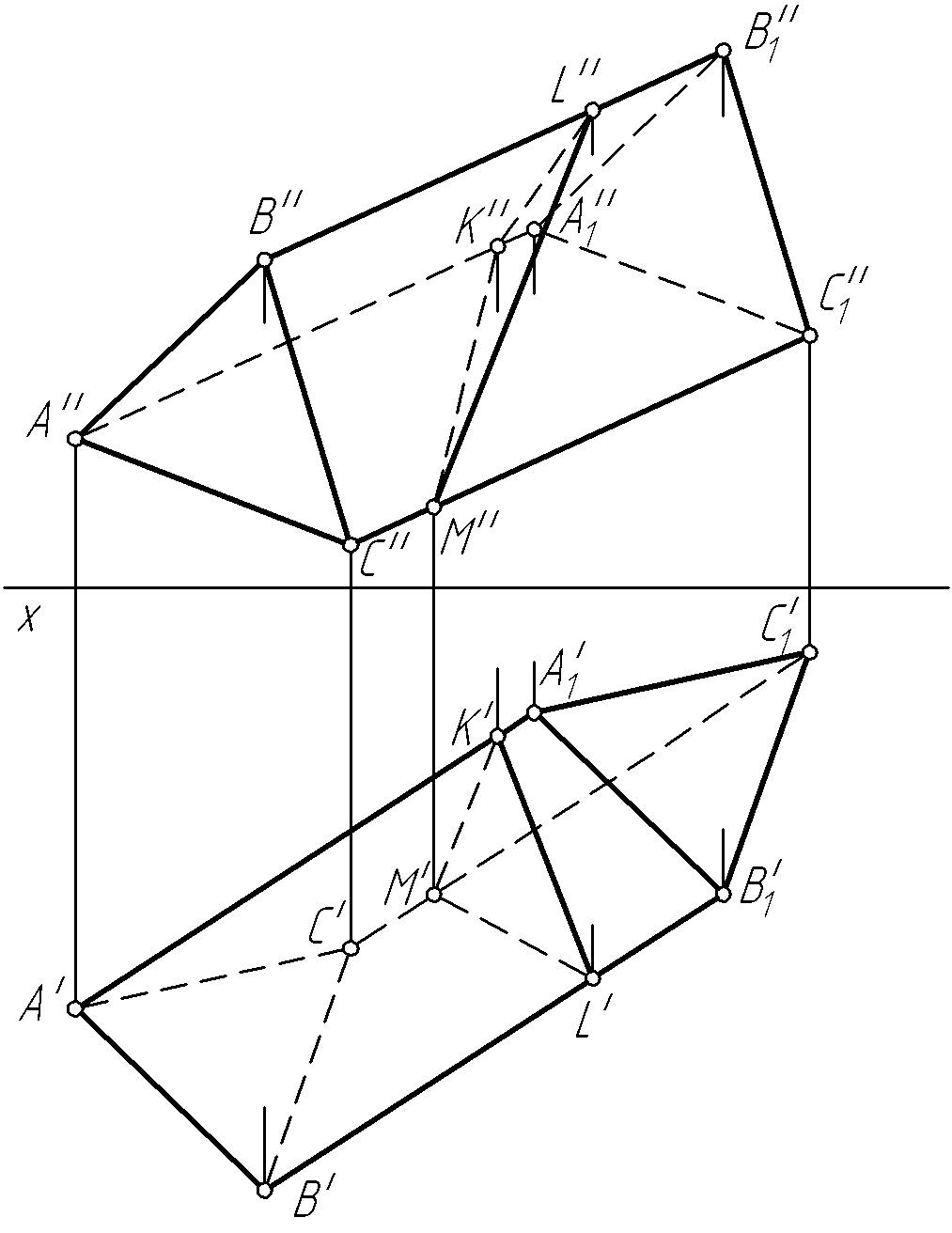
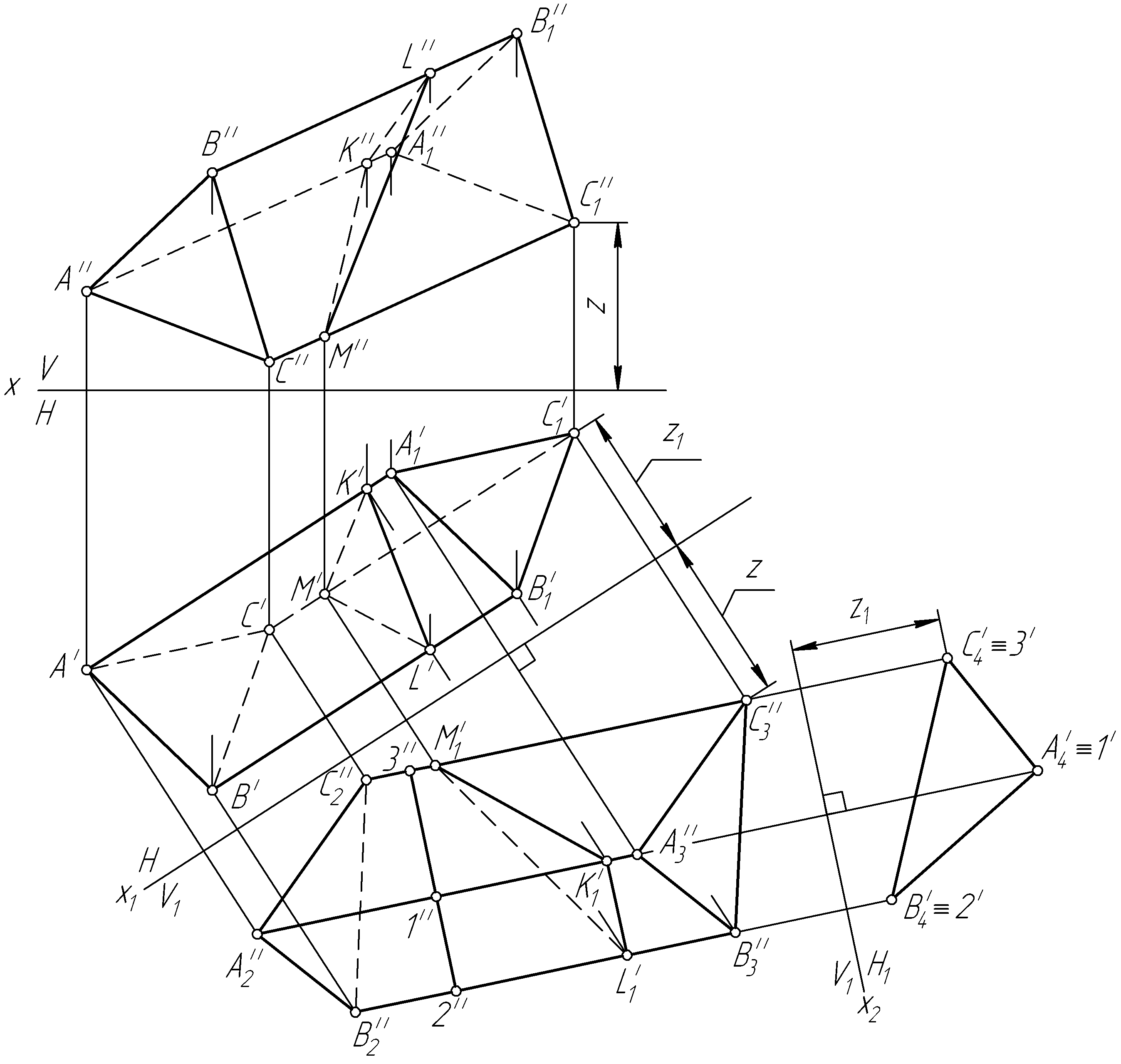
Пример 50. Построить полную развертку треугольной призмы и нанести на нее ломаную линию KLMK, принадлежащую поверхности призмы (рис. 107, а).

Решение. Развертка призмы представляет собой совокупность ее боковых граней (в данном случае параллелограммов) и двух равных оснований (плоских треугольников).

Построение развертки призмы сводится к определению ее нормального сечения. Нормальным сечением называется сечение призмы плоскостью, перпендикулярной ее ребрам. Такая плоскость пересекает призму по некоторому многоугольнику, стороны которого перпендикулярны ребрам призмы и равны расстояниям между соответствующими соседними ее ребрами.

Для построения развертки боковой поверхности призмы вначале определяем натуральную величину ее ребер (рис. 107, б). Для этого вводим дополнительную фронтальную плоскость проекций V₁, параллельную ребрам призмы, и строим проекции призмы в новой системе плоскостей проекций . При этом новая ось проекцийx₁ будет параллельна горизонтальной проекции любого бокового ребра призмы (например, x₁║А'А₁'). На плоскость проекций V₁ ребра призмы проецируются без искажения (АА₁ = А₂''А₃'', ВВ₁ = В₂''В₃'', СС₁ = С₂''С₃'').

Далее определяем натуральную величину произвольного нормального сечения призмы (рис. 107, б). Для этого выбирается новая горизонтальная плоскость проекций Н₁, перпендикулярная ребрам призмы. При этом новая ось проекций x₂ будет перпендикулярна фронтальной проекции на плоскость V₁ любого бокового ребра призмы (например, x₂ А₂''А₃''). На плоскость Н₁ ребра спроецируются в точки А₄', В₄' и С₄'. Треугольник 1' 2' 3' определяет натуральную величину нормального сечения призмы.

а)

Рис. 107

На произвольной горизонтальной прямой откладываем расстояния между соседними ребрами призмы (1₀2₀ = 1'2', 2₀3₀ = 2'3', 3₀1₀ = 3'1') (рис. 107, в).

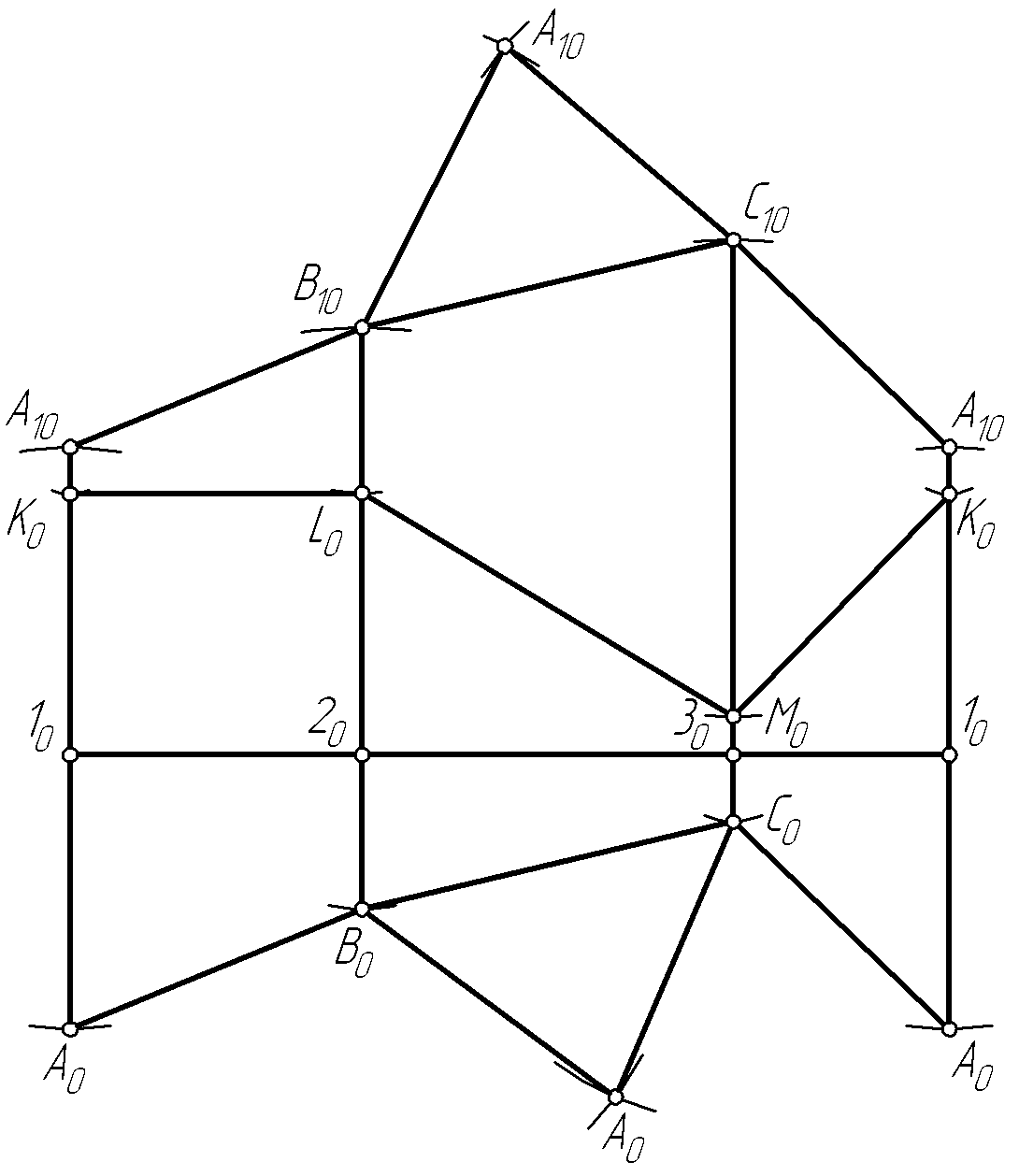
Через точки 1₀, 2₀ и 3₀ спрямленного нормального сечения проводим ребра призмы перпендикулярно нормальному сечению (А₀А₁₀ 1₀1₀, В₀В₁₀ 1₀1₀, С₀С₁₀ 1₀1₀). На развертке от спрямленного сечения 1₀1₀ откладываем на ребрах призмы расстояния от нормального сечения до соответствующих вершин призмы (1₀А₀ = 1'' А₂'', 1₀А₁₀ = 1'' А₃'' и т.д.). В заключение соединяем точки А₀, В₀, С₀ и А₁₀, В₁₀ и С₁₀ ломаными линиями и к развертке боковой поверхности призмы пристраиваем ее основания. Построение оснований призмы А₀ В₀ С₀ и А₁₀ В₁₀ С₁₀ осуществляется по трем известным сторонам.

Для нанесения на развертку призмы ломаной линии KLMK, принадлежащей ее поверхности, необходимо вначале спроецировать ее на плоскость V₁ (на эту плоскость проекций ребра призмы проецируются в натуральную величину) (рис. 107, б). Затем на развертке откладываем расстояния от точек K, L и M до соответствующих вершин призмы (K₀A₁₀ = K₁''А₃'', L₀B₁₀ = =L₁''B₃'', M₀C₁₀ = M₁''C₃'').

б)

Рис. 107. Продолжение

в)

Рис. 107. Окончание

Развертывание кривых поверхностей. К развертываемым кривым поверхностям относятся только линейчатые поверхности (т.е. поверхности, образующая которых – прямая линия) с пересекающимися смежными образующими. Такие поверхности называются также торсовыми. К торсовым относятся цилиндрические, конические поверхности и поверхности с ребром возврата. Рассмотрим примеры построения разверток некоторых кривых поверхностей.

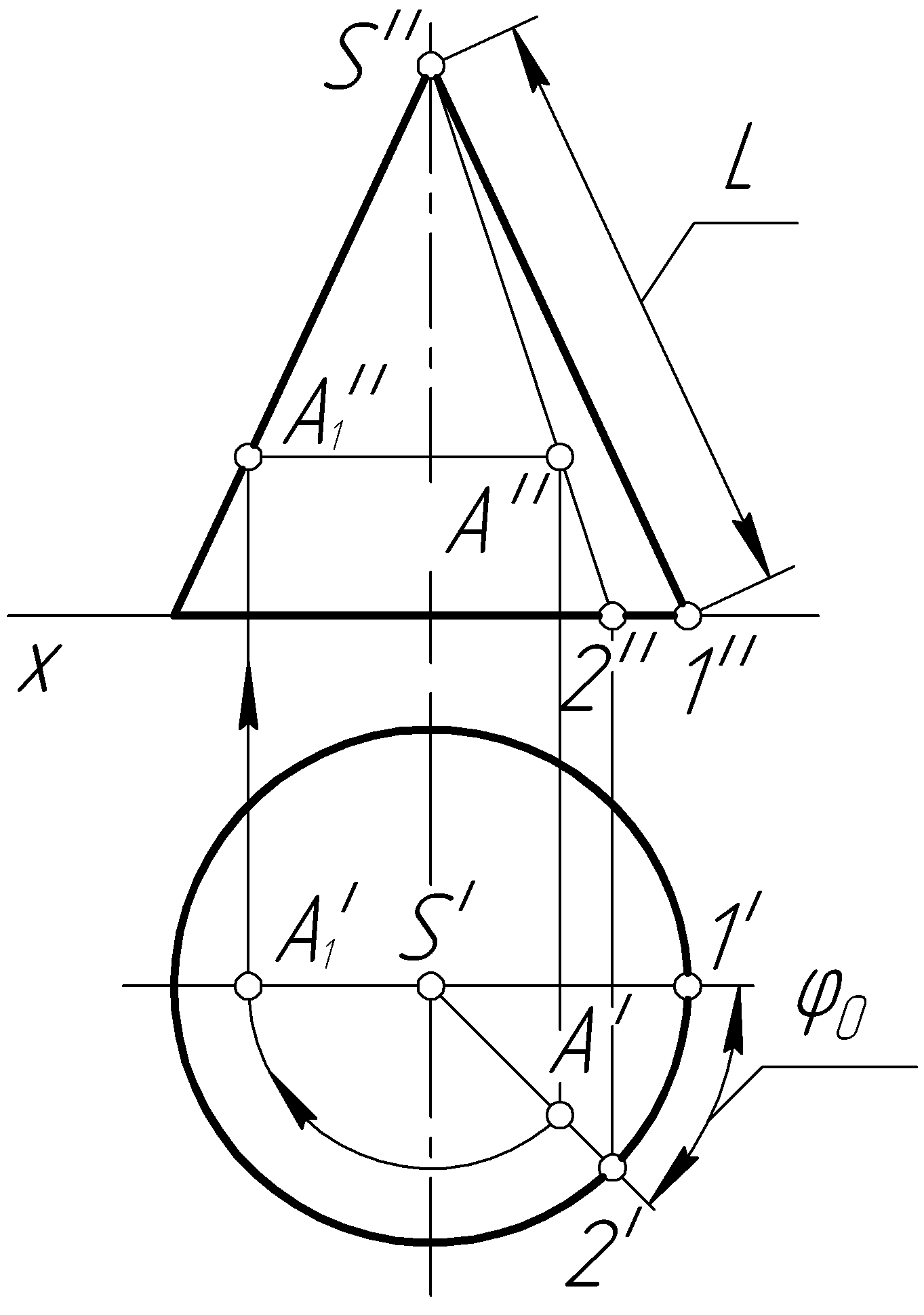
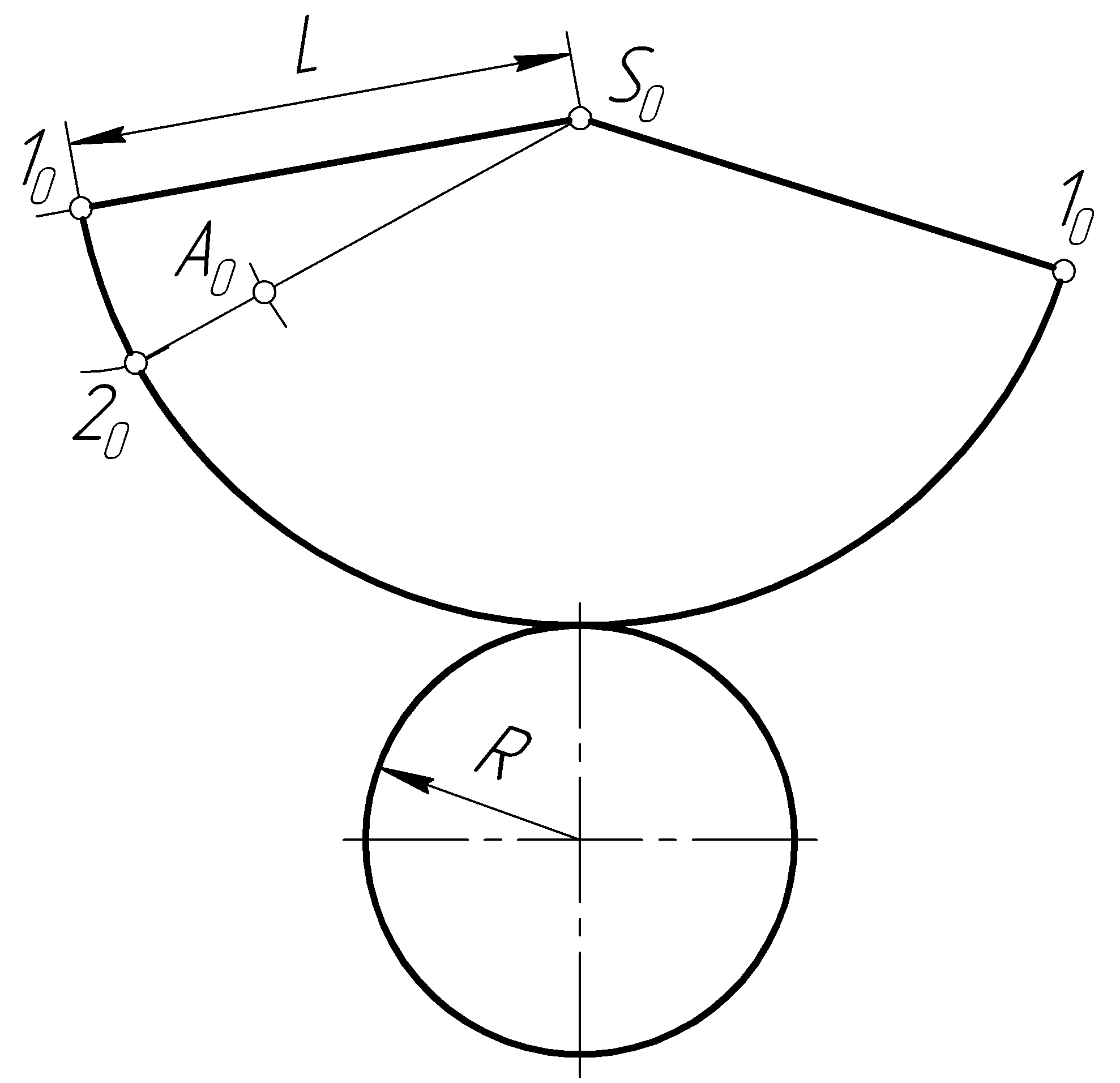
Пример 51. Построить полную развертку прямого кругового конуса и нанести на нее точку А, лежащую на поверхности конуса (рис. 108, а).

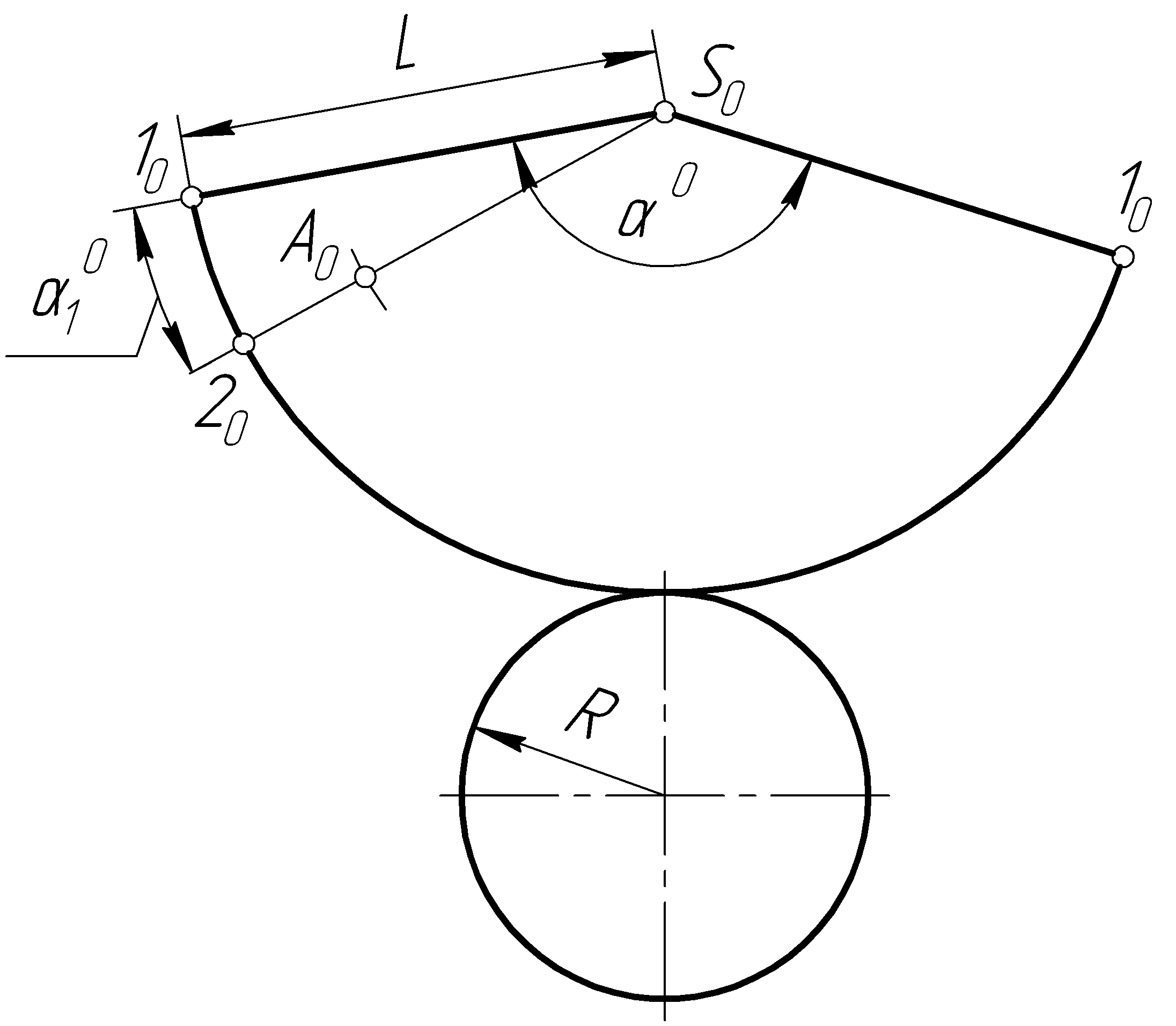
Решение. Полная развертка конуса состоит из развертки его боковой поверхности и окружности основания (рис. 108, в,д).

Развертка боковой поверхности прямого кругового конуса представляет собой круговой сектор с центром в произвольной точке S₀, соответствующей вершине конуса, радиуса L и с углом при вершине, равным

,

где R – радиус окружности основания конуса; L – длина образующей этого конуса (рис. 108, б).

а)	б)

в)

Рис. 108

г)	д)

Рис. 108. Продолжение

К развертке боковой поверхности в любом месте пристраивается окружность основания, радиус которой R.

Построение на развертке точки А₀, соответствующей точке А (А', А''), лежащей на поверхности конуса, осуществляется следующим образом (рис. 108, б). Вращением вокруг оси конуса определяется натуральная величина отрезка SA (S'А', S''А'') образующей, которой принадлежит точка А (А', А''). От первой образующей на развертке (рис108, в) вдоль дуги развертки основания откладываем точку 2₀ так, чтобы угол с центром в точке S₀ был равен

,

где – величина угла с вершиной вS', одна из сторон которого является горизонтальной проекцией первой образующей развертки, а вторая – горизонтальная проекция образующей, которой принадлежит точка А (А', А'').

Соединяем точку 2₀ с S₀ и получаем положение на развертке образующей, на которой лежит точка А. Откладываем вдоль этой образующей от точки S₀ натуральную величину отрезкаSA.

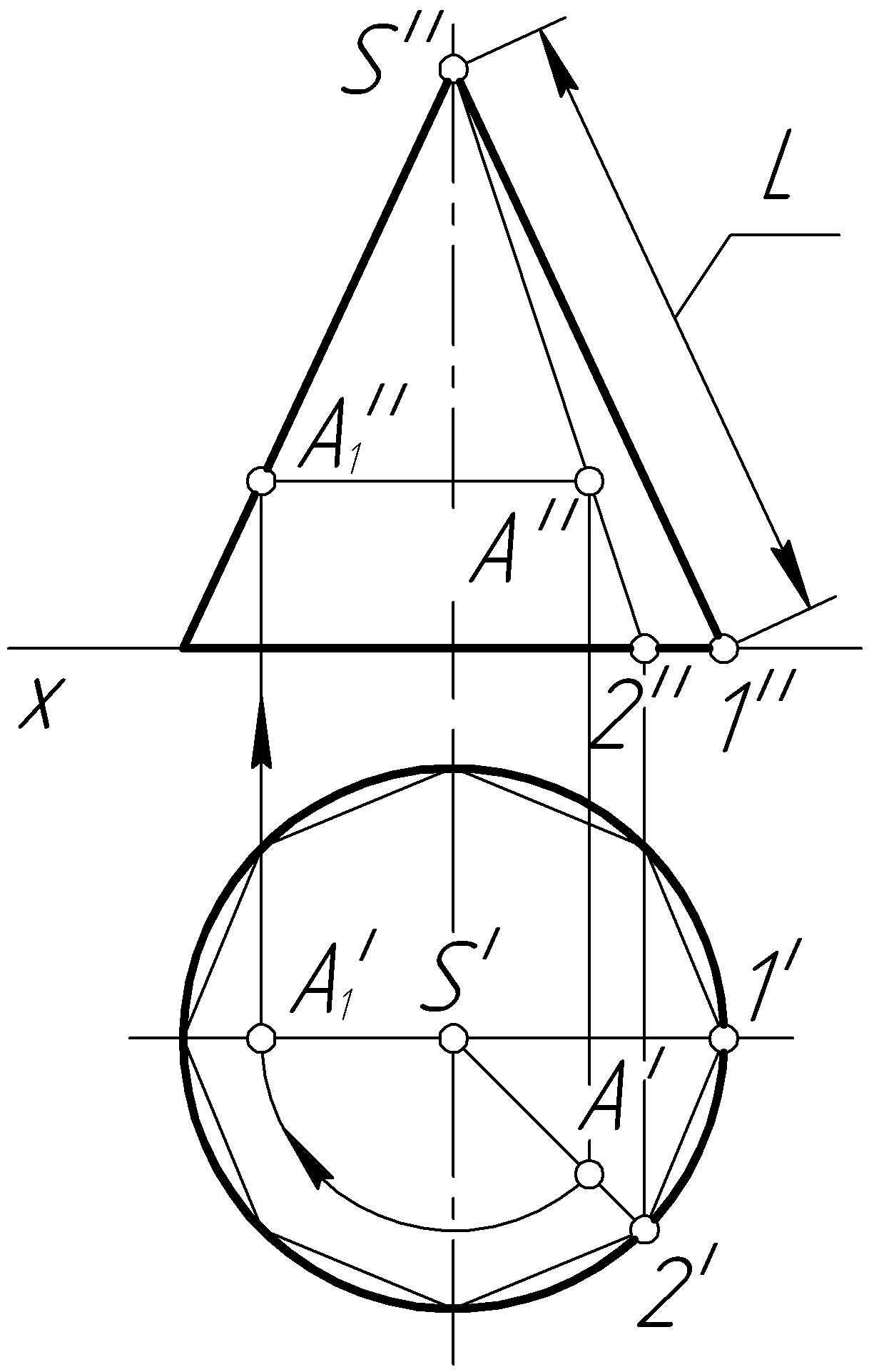
На практике чаще строят приближенную развертку конуса. Для этого в конус вписывают пирамиду с вершиной в вершине конуса и основанием, вписанным в основание конуса (рис. 108, г). Чем больше граней у пирамиды, тем точнее получается развертка конуса. Построение развертки пирамиды подробно рассмотрено в примерах 46 и 47. Для построения точки А на развертке (рис. 108, д) определяется ее положение на какой-либо образующей конуса. Эта образующая переносится на развертку (длина дуги 1₀2₀ на развертке равна длине соответствующей хорды 1'2' на горизонтальной проекции поверхности конуса). На построенной образующей от точки S₀ откладываем натуральную величину отрезкаSA.

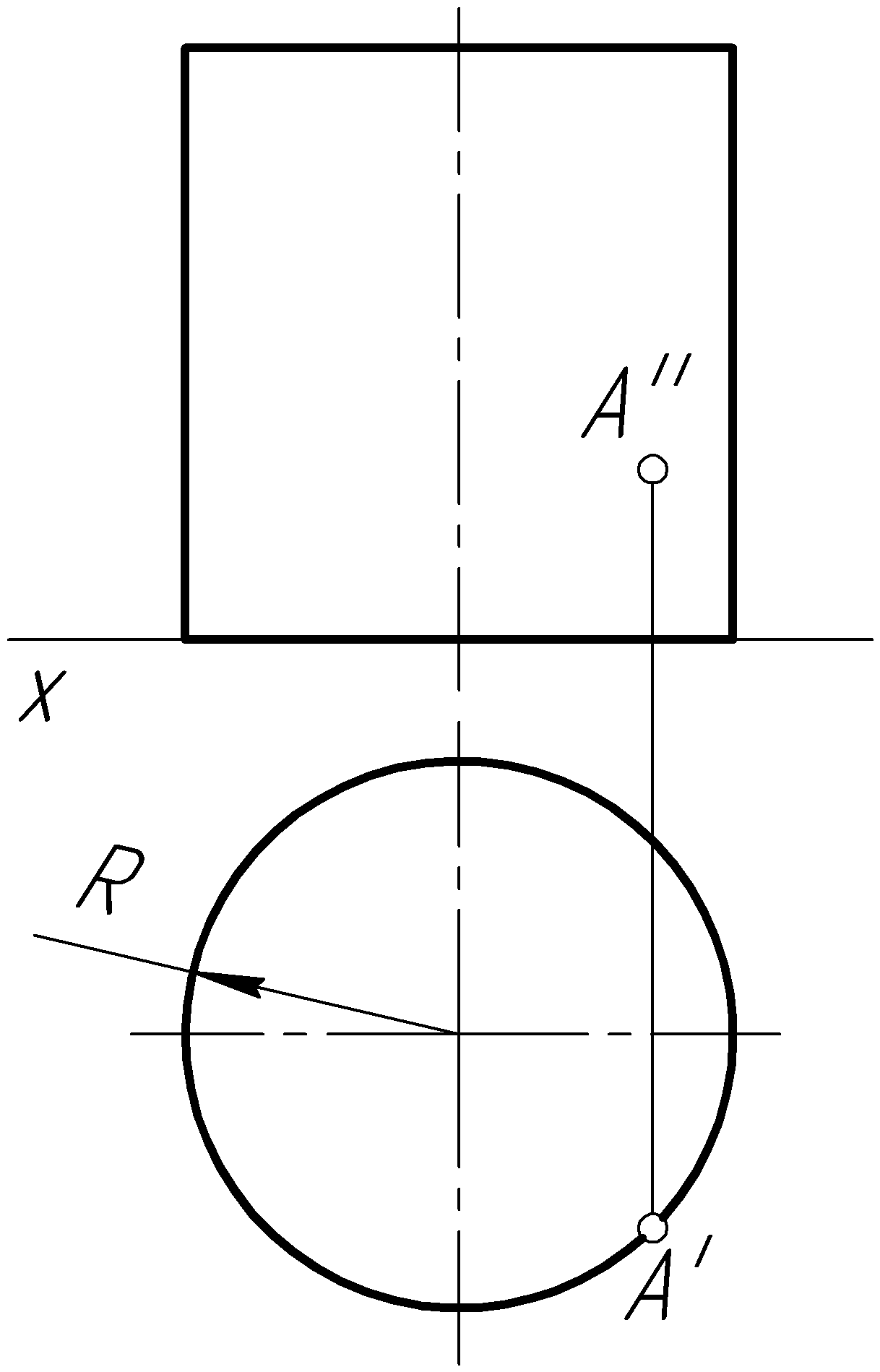
Пример 52. Построить полную развертку прямого кругового цилиндра и нанести на нее точку А, лежащую на поверхности цилиндра (рис. 109, а).

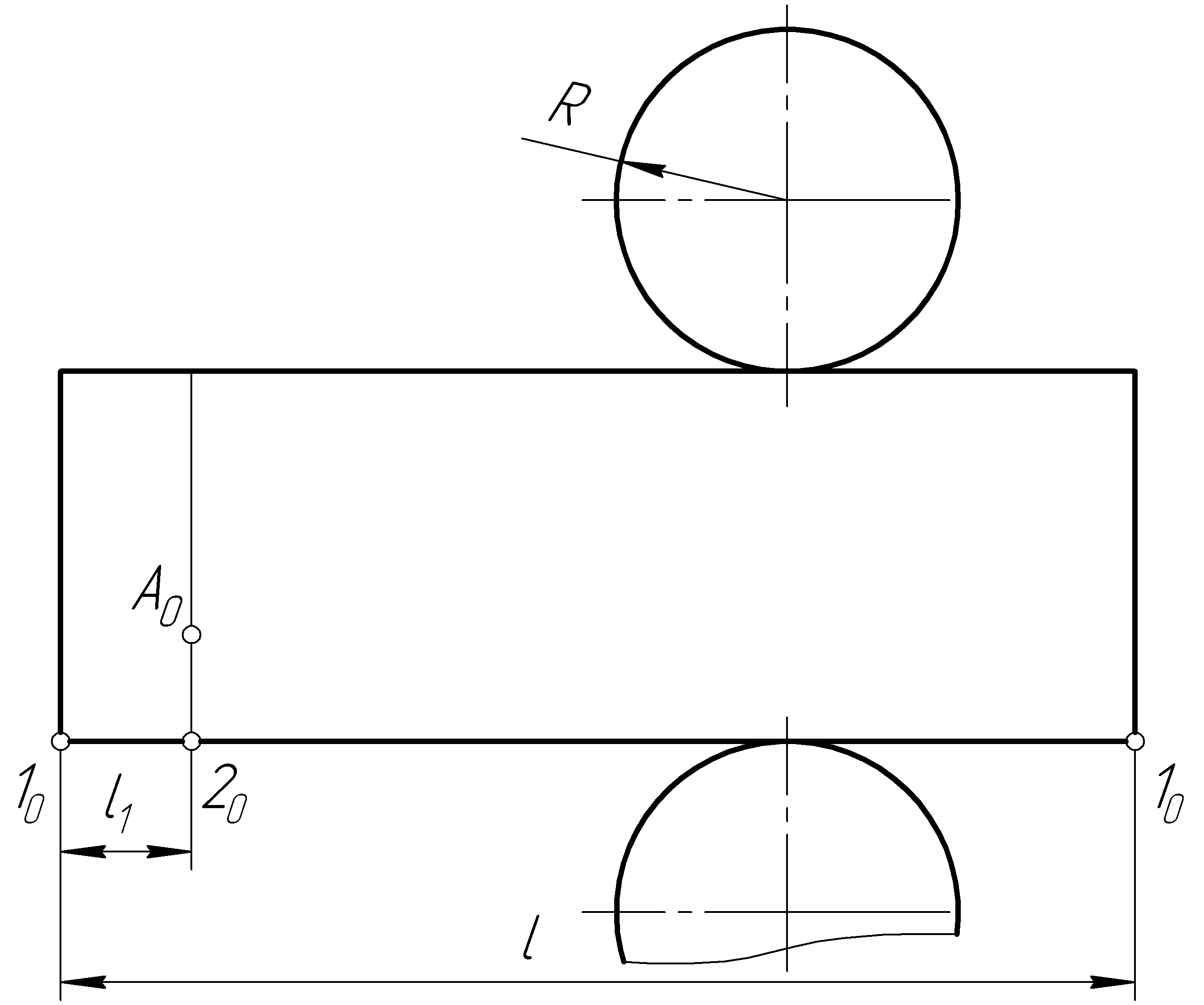
Решение. Полная развертка цилиндра состоит из развертки его боковой поверхности и двух окружностей оснований (рис. 109, в, д).

Развертка боковой поверхности прямого кругового цилиндра представляет собой прямоугольник, высота которого равна высоте цилиндра, а длина – длине окружности его основания:

,

где R – радиус окружности основания цилиндра (рис. 109, б).

К развертке боковой поверхности в любом месте пристраиваются две окружности оснований, радиус которых R.

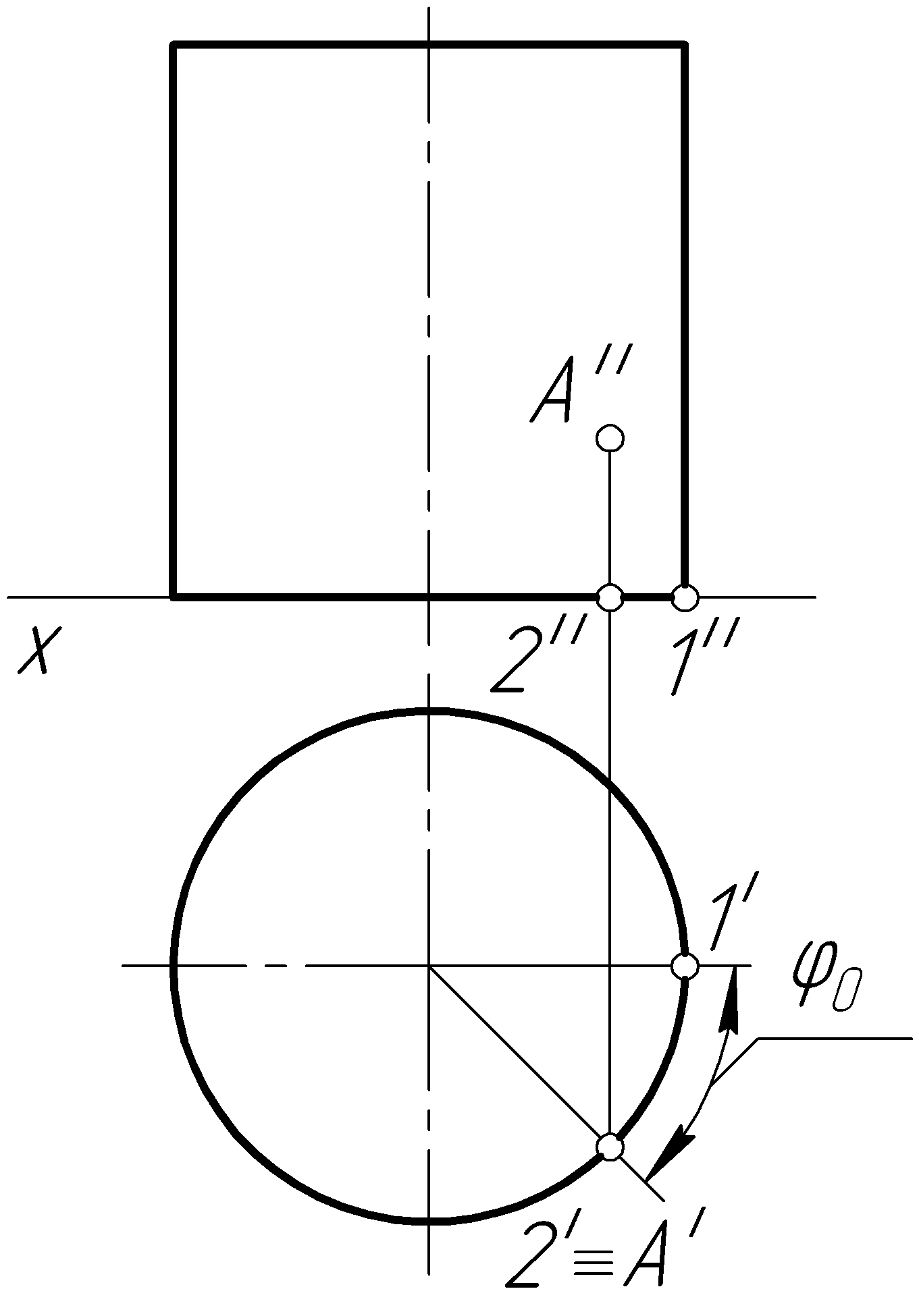
Построение на развертке точки А₀, соответствующей точке А (А', А''), лежащей на поверхности цилиндра, осуществляется следующим образом (рис. 109, б). От первой образующей на развертке вдоль ее длины откладываем точку 2₀ так, чтобы отрезок 1₀2₀ = l₁ был равен

,

где – величина центрального угла дуги1'2'.

Через точку 2₀ проводим образующую, перпендикулярную развертке окружности основания, и откладываем вдоль этой образующей отрезок 2₀А₀, равный натуральной величине 2''А'' отрезка 2A.

Приближенная развертка цилиндра строится аналогично развертке конической поверхности. Для этого в цилиндр вписывают прямую призму с основаниями, вписанными в основания цилиндра (рис. 109, г). Естественно, что чем больше граней у призмы, тем точнее получается развертка цилиндра. Построение развертки призмы подробно рассмотрено выше. Затем определяют положение точки на какой-либо образующей, и эта точка переносится на развертку. Длина дуги 1₀2₀ на развертке

а)	б)

в)

Рис. 109

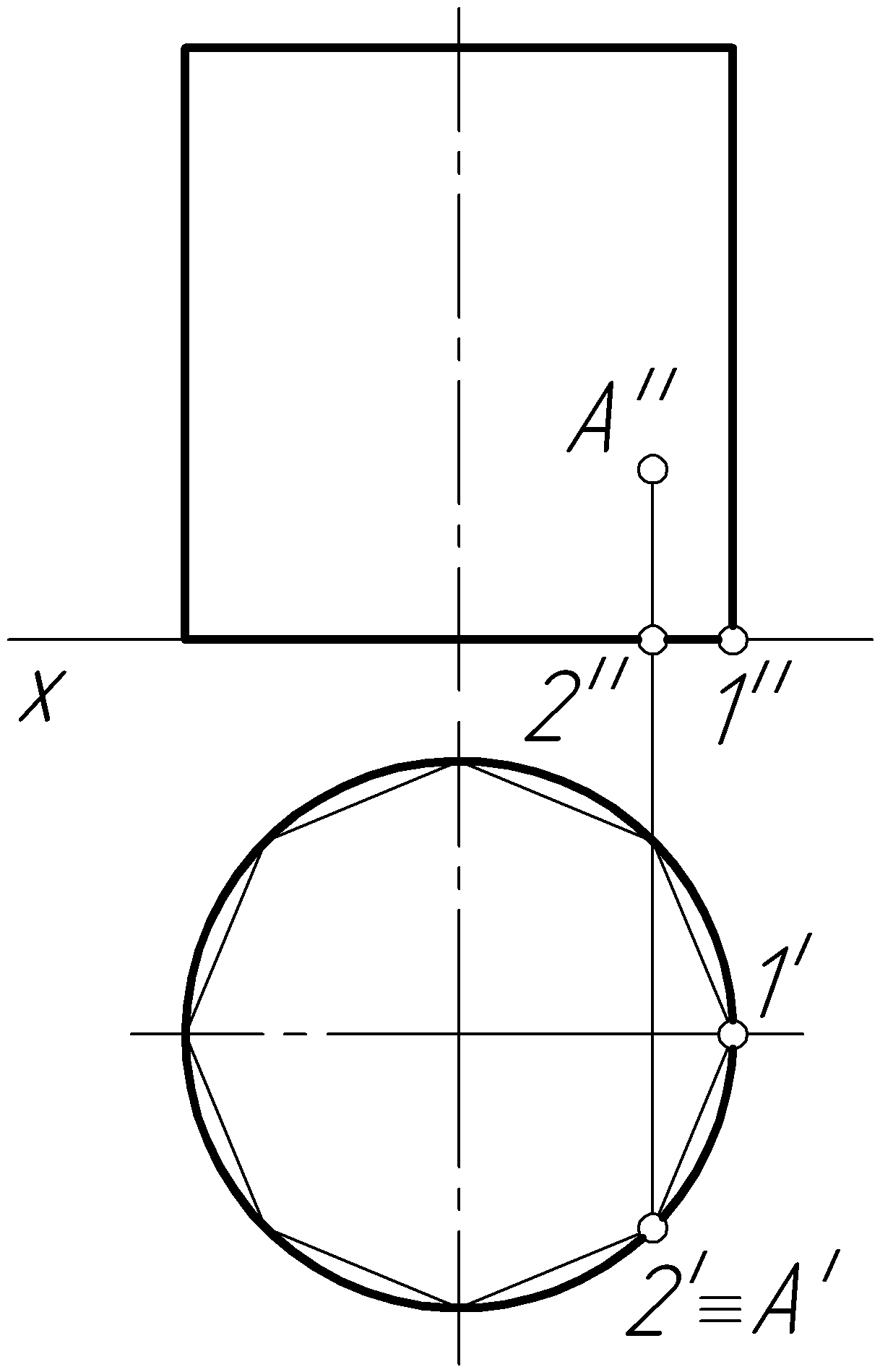
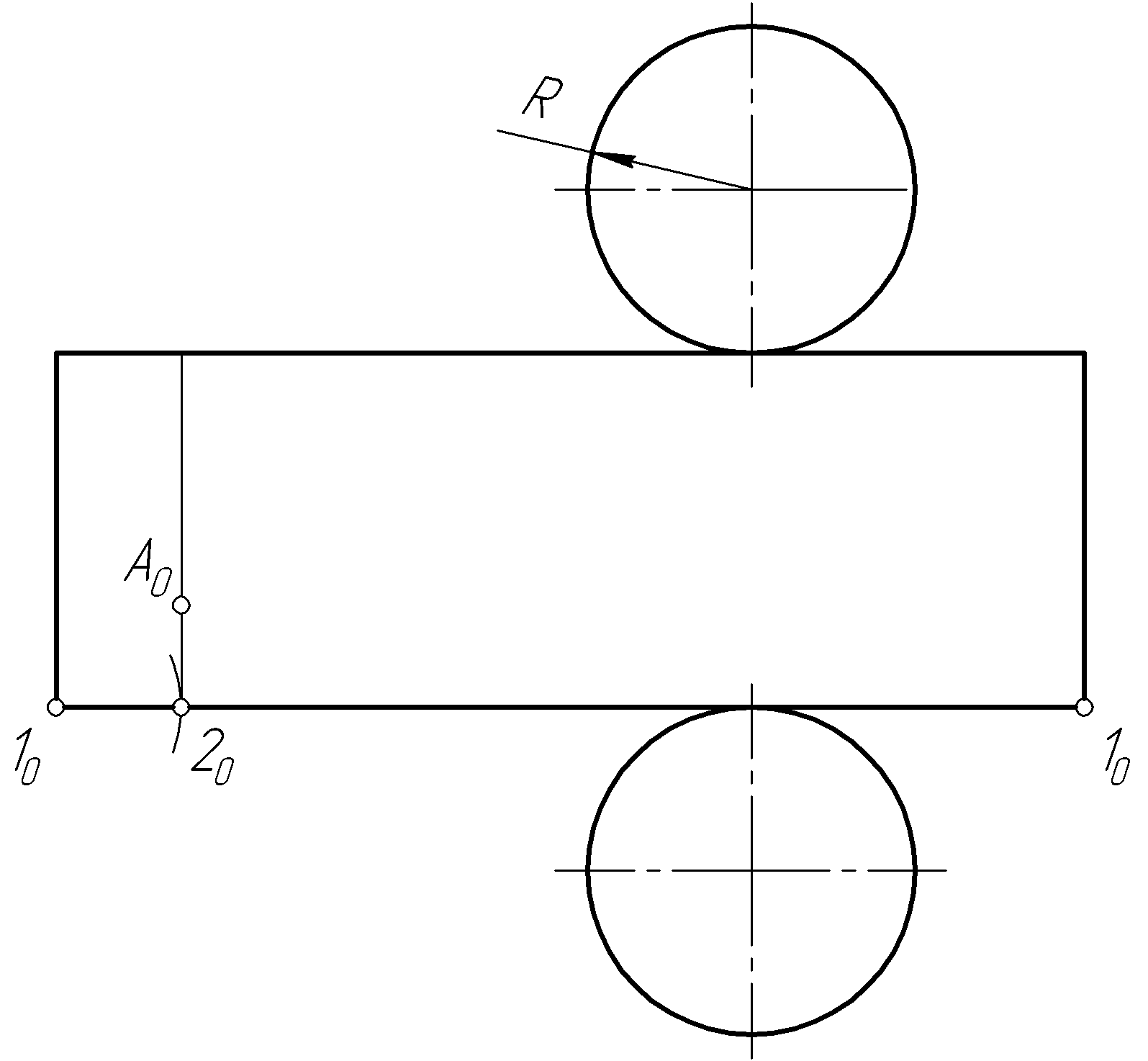
г)

д)

Рис. 109. Продолжение

равна длине соответствующей хорды 1'2' на горизонтальной проекции поверхности цилиндра (рис. 109, д).