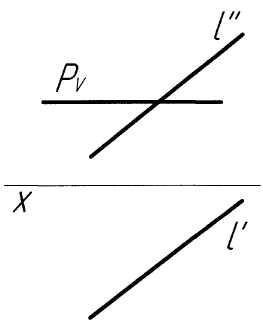Принятые обозначения

Точки в пространстве		1) прописными буквами латинского алфавита: А, В, С,…; 2) цифрами: 1, 2, 3,…
Линии в пространстве		1) по точкам, определяющим линию; 2) строчными буквами латинского алфавита: a, b, c,…
Плоские углы		1) строчными буквами греческого алфавита: α, β, γ,…; 2) тремя точками, вторая из которых определяет вершину угла: АВС, …
Плоскости		1) по точкам и прямым, определяющим плоскость; 2) прописными буквами латинского алфавита: P, Q, R…
Плоскости проекций: горизонтальная фронтальная профильная		Н V W
Дополнительные плоскости проекций: горизонтальная фронтальная профильная		Н1, Н2, Н3, … V1, V2, V3, … W1, W2, W3, …
Начало координат		прописной буквой О
Оси проекций: абсцисс ординат аппликат		x y z

Проекции точек: на горизонтальную плоскость проекций на фронтальную плоскость проекций на профильную плоскость проекций		А', В', С'… А'', В'', С''… А''', В''', С'''…
Проекции линий		1) по проекциям точек, определяющих линию; 2) строчными буквами латинского алфавита с одним, двумя или тремя штрихами, по аналогии с проекциями точек: а', b', c'…; a'', b'', c''…; a''', b''', c'''…
Проекции плоскости		1) по проекциям точек и прямых, определяющих плоскость; 2) следами
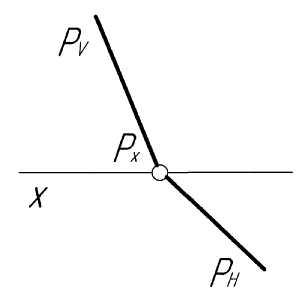
Следы плоскости: горизонтальный фронтальный профильный точки схода следов		PН, QН, … PV, QV, … PW, QW, … Px, Py, Pz; Qx, Qy, Qz;…
Прямые особого положения в плоскости: горизонталь фронталь профильная		h f p

Взаимное положение прямой и плоскости и плоскостей между собой Примеры решения задач

Пересечение прямой линии с плоскостью. Для построения точки пересечения прямой с плоскостью необходимо выполнить следующее:

1) через заданную прямую провести вспомогательную плоскость, перпендикулярную одной из плоскостей проекций;

2) построить линию пересечения заданной и вспомогательной плоскостей;

3) определить искомую точку пересечения прямой с плоскостью как точку пересечения заданной прямой и построенной линии пересечения плоскостей.

Если объекты проецирования занимают относительно плоскостей проекций частное положение, то решение задачи упрощается.

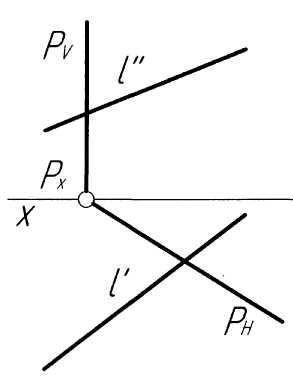
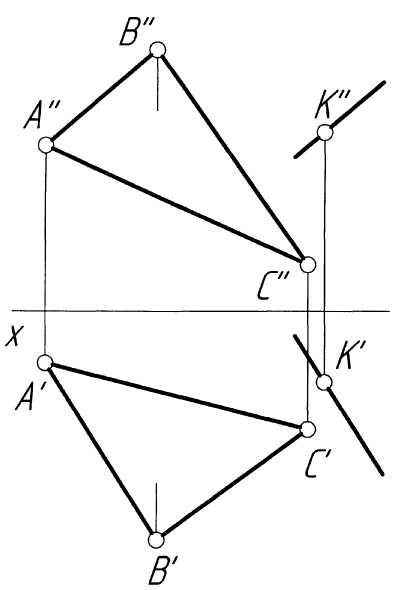
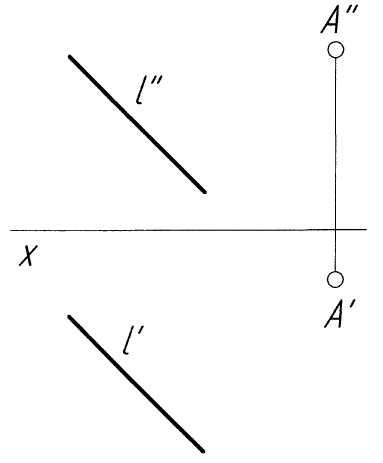
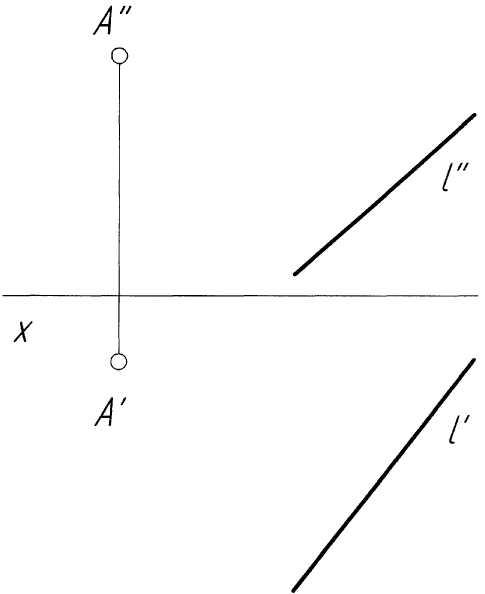
Пример 1. Построить точку пересечения прямойlс плоскостьюР, заданной следами и перпендикулярной горизонтальной плоскости проекций (рис. 1,а).

Решение. Поскольку плоскость Р (Р_Н, Р_V) является горизонтально-проецирующей, то проекция K' точки пересечения прямой с плоскостью должна принадлежать одновременно и проекции l' и следу Р_Н (рис. 4, б). По проекции K' точки пересечения строим ее проекцию K'', исходя из условия принадлежности точки K прямой l. В заключение определяем видимость элементов чертежа методом конкурирующих точек. Конкурирующими называются такие точки пространства, у которых одноименные проекции на одной из плоскостей проекций совпадают. Считается, что наблюдатель смотрит на плоскости проекций из бесконечности, а его луч зрения параллелен проецирующему лучу. Та из двух конкурирующих точек, которая расположена ближе к наблюдателю (а значит, дальше от плоскости проекций) является видимой.

а)	б)
Рис. 1

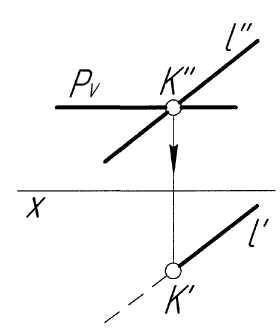
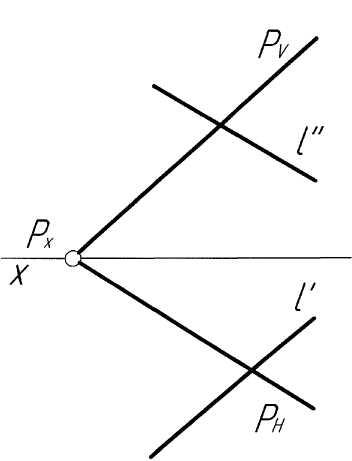
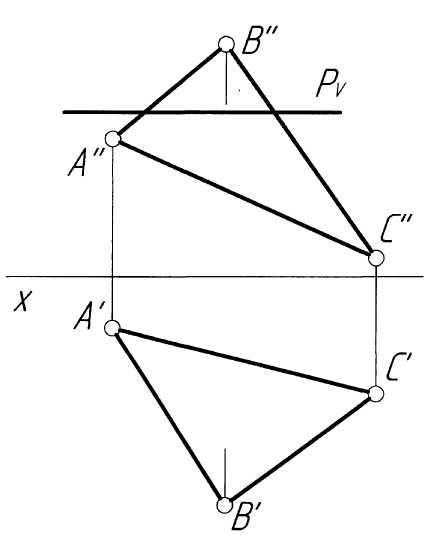
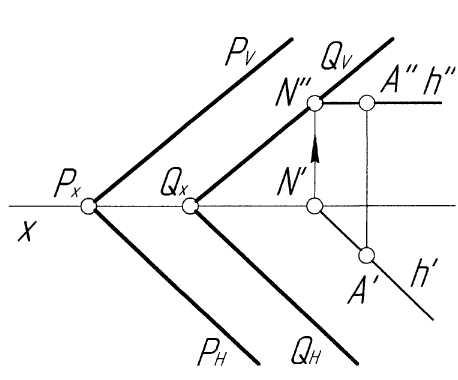
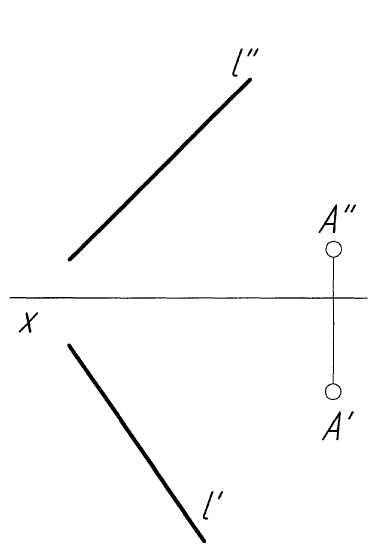
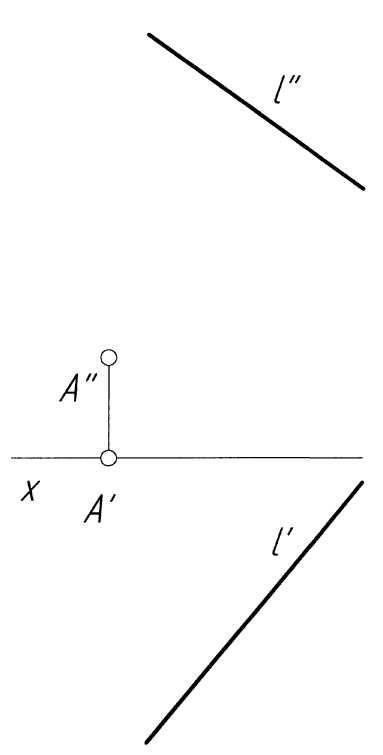
Пример 2. Построить точку пересечения прямойlс плоскостьюР, заданной следами и параллельной горизонтальной плоскости проекций (рис. 2,а).

Решение.Решение задачи аналогично примеру 1. ПроекциюK''точки пересечения прямой с плоскостью определяем как точку пересечения следаР_Vс проекциейl''(рис. 2,б). По проекцииK''строим проекцию K'искомой точки, исходя из условия принадлежности ее прямойl. В заключение определяем видимость элементов чертежа.

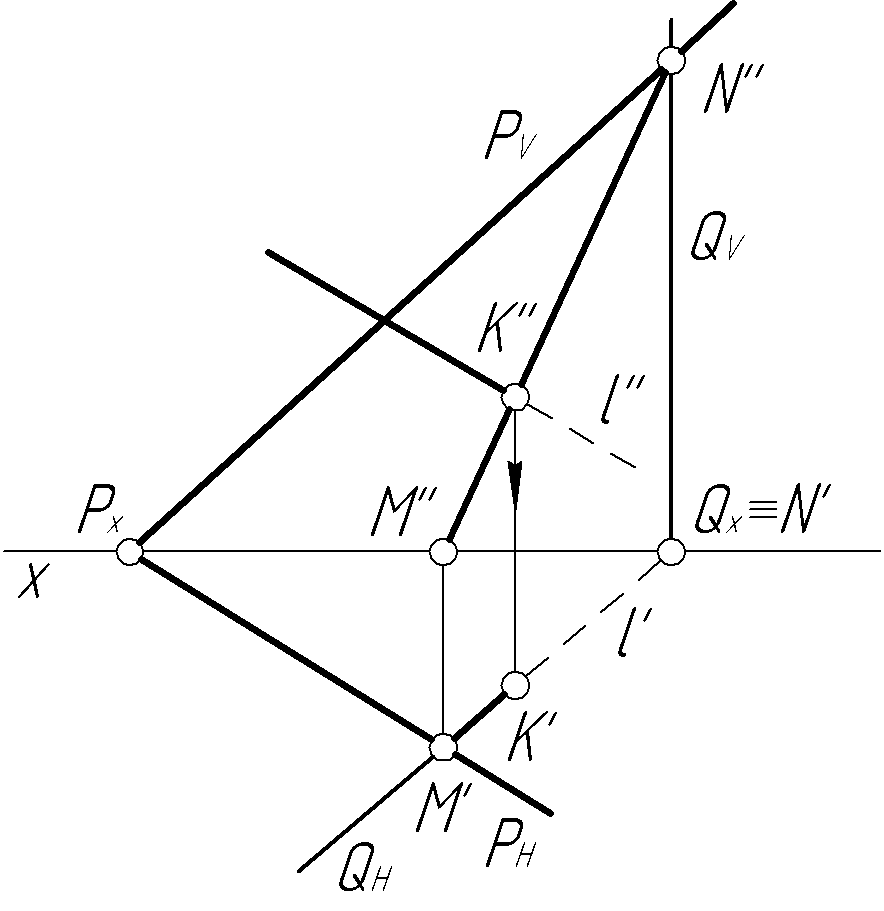
Пример 3. Построить точку пересечения прямой l с плоскостью Р общего положения (рис. 3, а).

а)	б)
Рис. 2

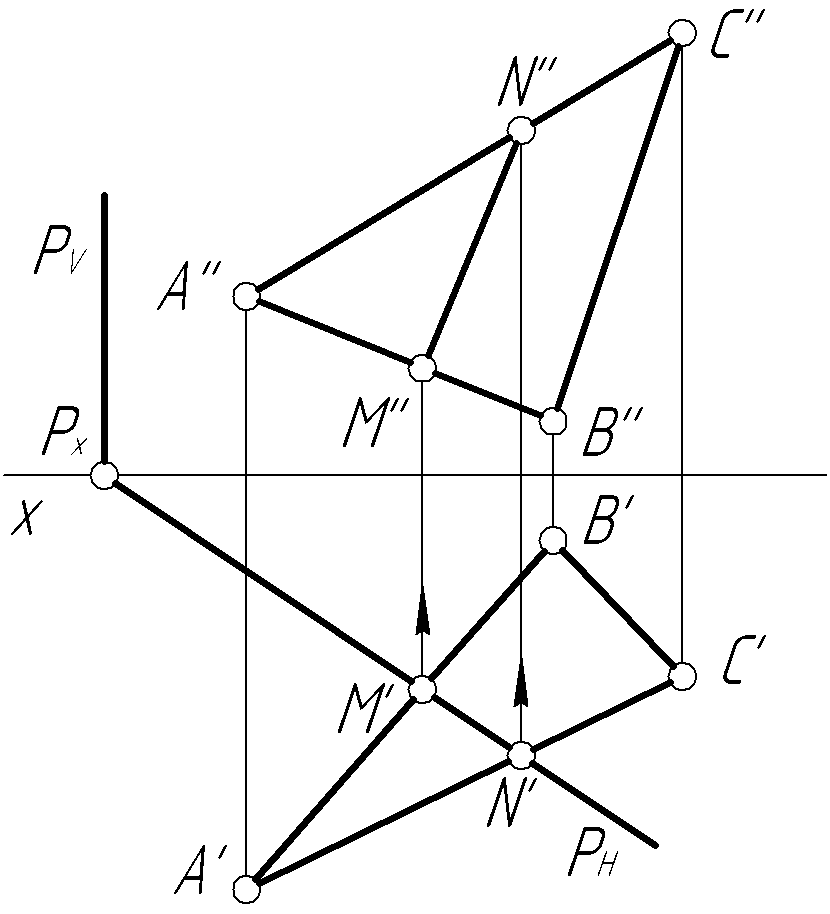
Решение. Решение задачи производим в следующей последовательности (рис. 3, б). Заключаем прямую l (l', l'') в горизонтально-проецирующую плоскость Q (Q_H, Q_V), задав ее следами. Строим точки M (M', M'') и N (N', N''), принадлежащие одновременно обеим плоскостям, и соединяем их прямой MN (M'N', M''N''), которая является линией пересечения плоскости Р (Р_Н, Р_V) с плоскостью Q (Q_H, Q_V). На фронтальной плоскости проекций прямая M''N'' пересекается с прямой l'' в точке K''. Далее строим проекцию K' искомой точки. Определяем видимость элементов чертежа.

а)	б)
Рис. 3

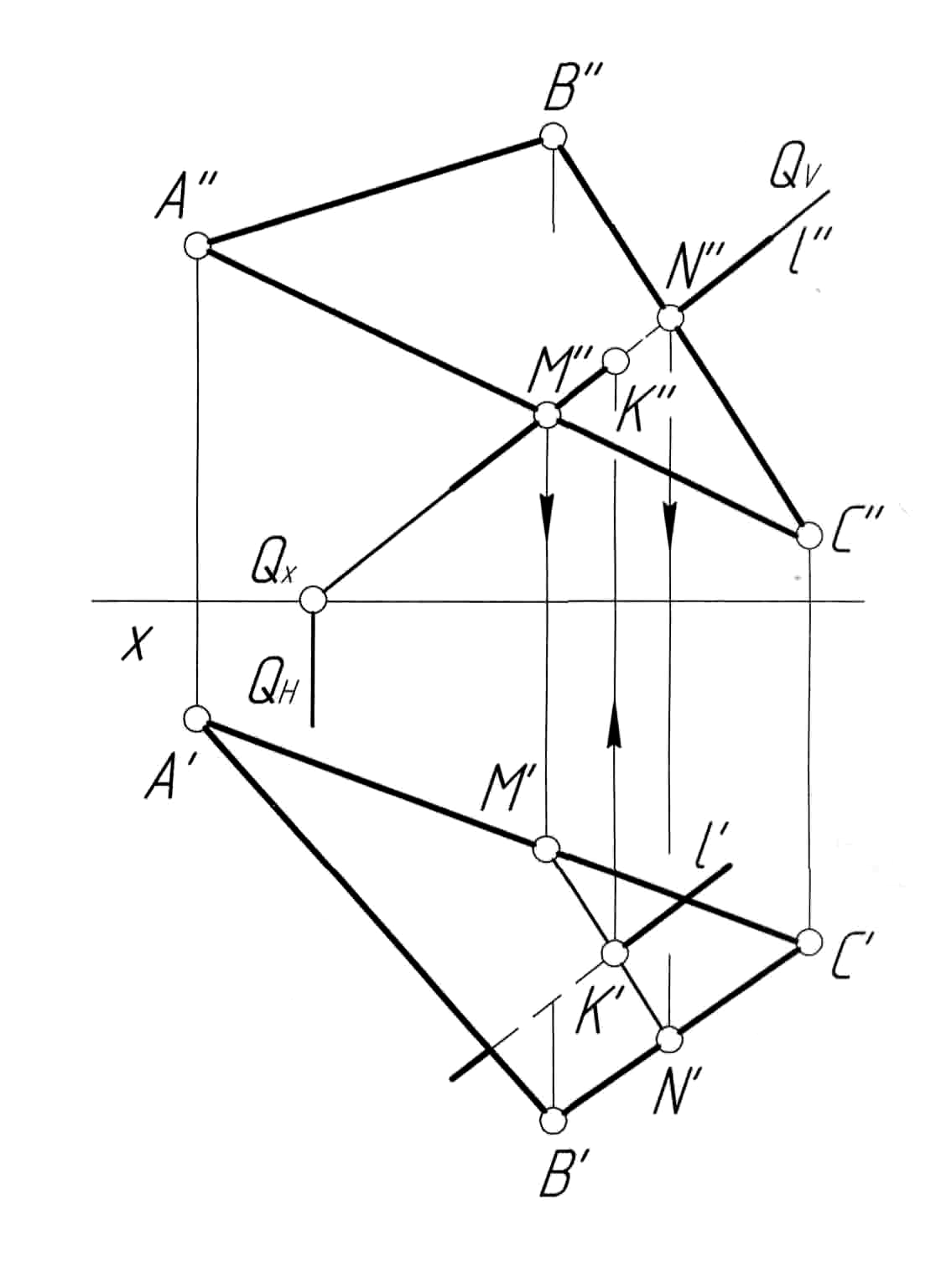
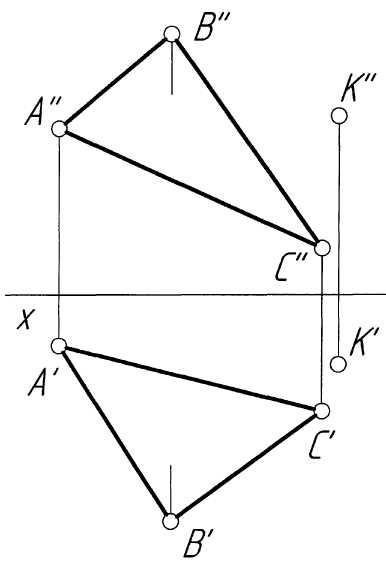
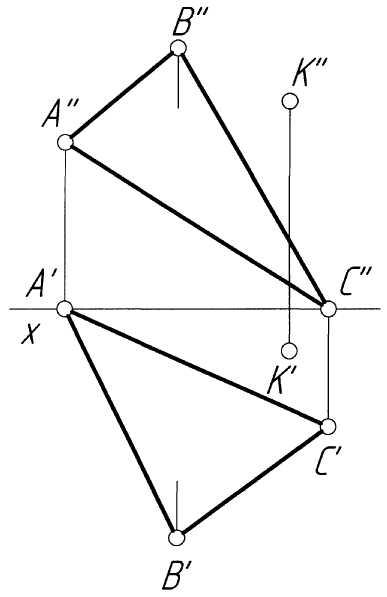
Пример 4.Построить точку пересечения прямойlс плоскостью треугольникаАВСобщего положения (рис. 4,а).

а)	б)
Рис. 4

Решение.Решение задачи (рис. 4, б) проводим в последовательности, аналогичной примеру 3. Заключаем прямуюl (l',l'') во фронтально-проецирующую плоскостьQ (Q_H, Q_V). Строим точкиM (M', M'') и N (N', N''), принадлежащие одновременно обеим плоскостям, и соединяем их прямой MN (M'N', M''N''), которая является линией пересечения плоскости треугольника АВС с плоскостью Q. На горизонтальной проекции прямая M'N' пересекается с прямой l' в точке K'. Далее строим проекцию K'' искомой точки. Определяем видимость элементов чертежа.

Перпендикулярность прямой и плоскости.Прямая перпендикулярна

плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим

в этой плоскости. В качестве таких двух пересекающихся прямых целесообразно выбирать горизонталь и фронталь плоскости, поскольку в этом случае образуются прямые углы, одна из сторон которых параллельна соответствующей плоскости проекций, а следовательно, по правилу проецирования плоского прямого угла эти прямые углы будут проецироваться на плоскости проекций без искажения. Таким образом, на эпюре фронтальную проекцию перпендикуляра проводят перпендикулярно фронтальной проекции фронтали, а горизонтальную проекцию – перпендикулярно горизонтальной проекции горизонтали.В том случае, если на эпюре плоскость задана следами, то проекции прямой, перпендикулярной плоскости, должны быть перпендикулярны к одноименным следам плоскости.

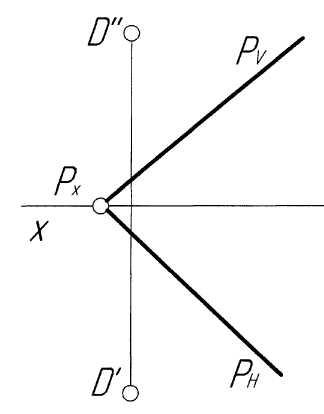
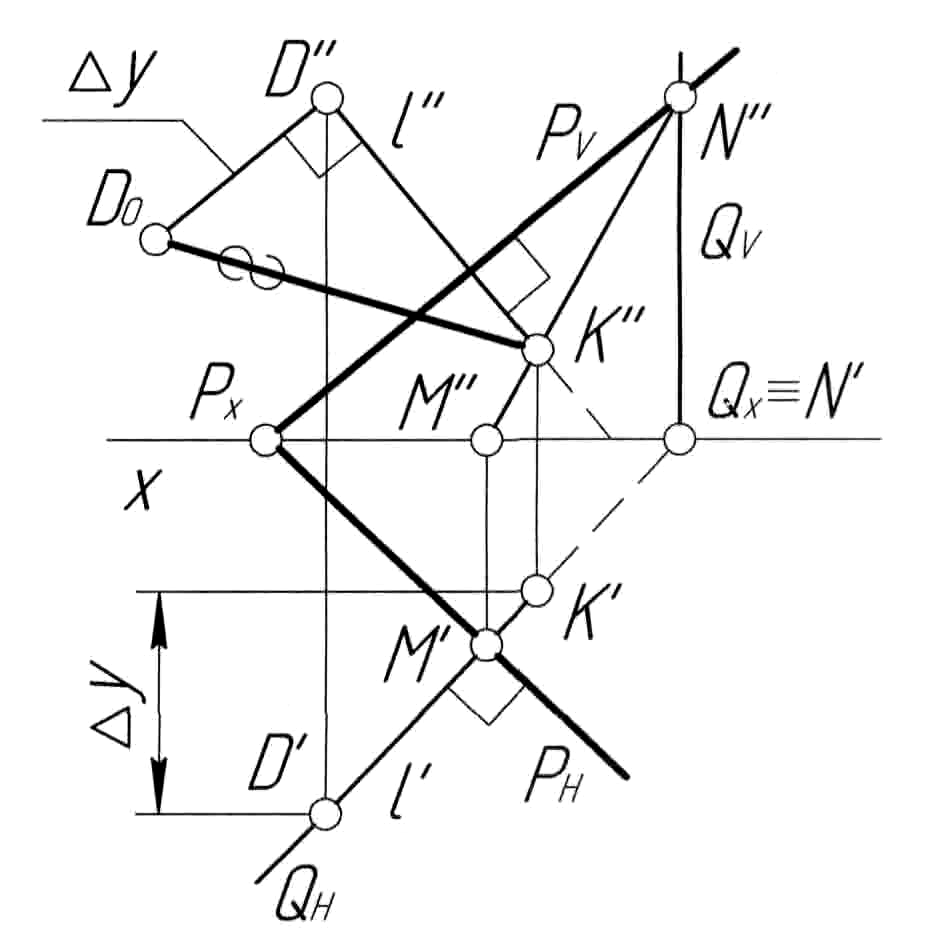
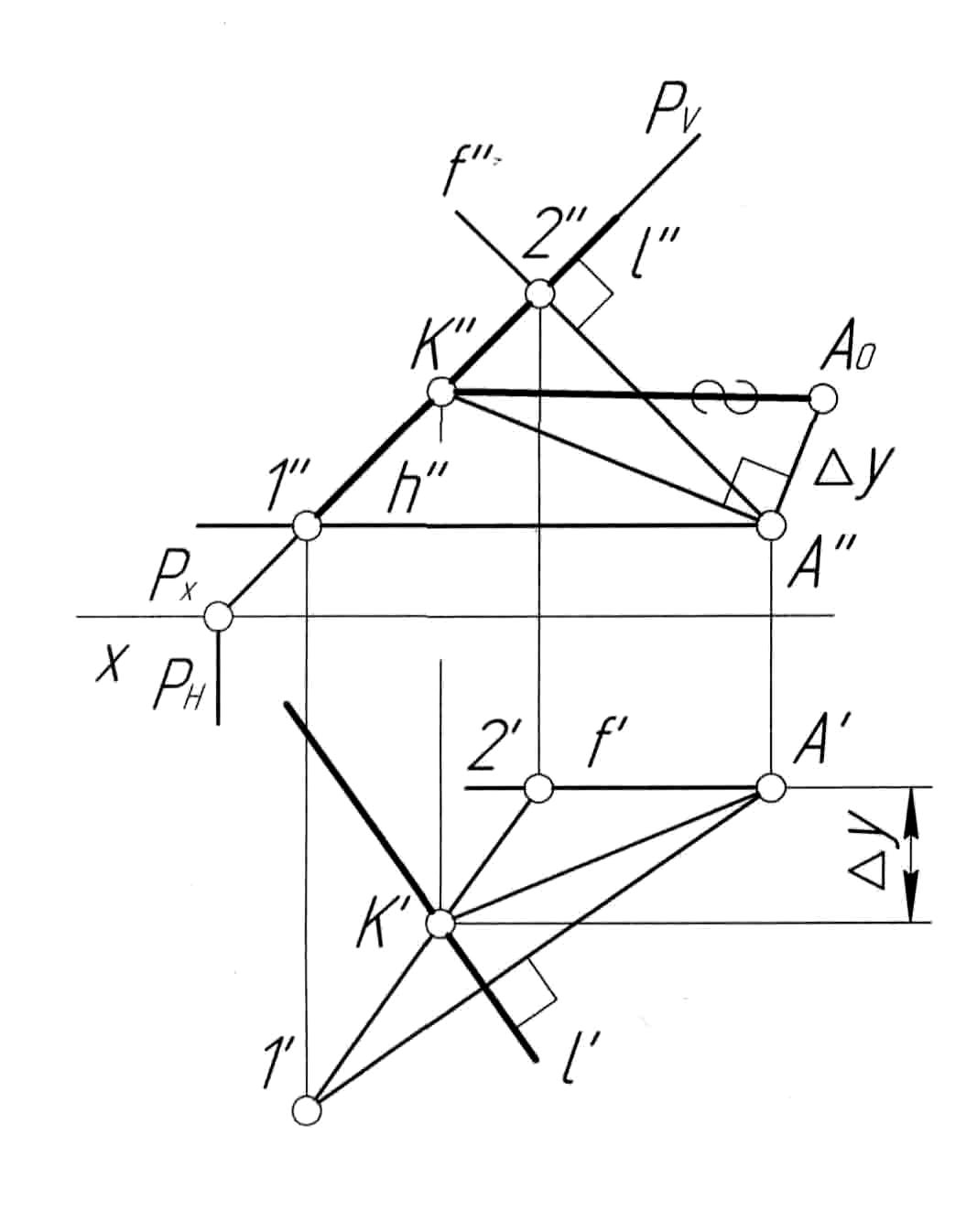
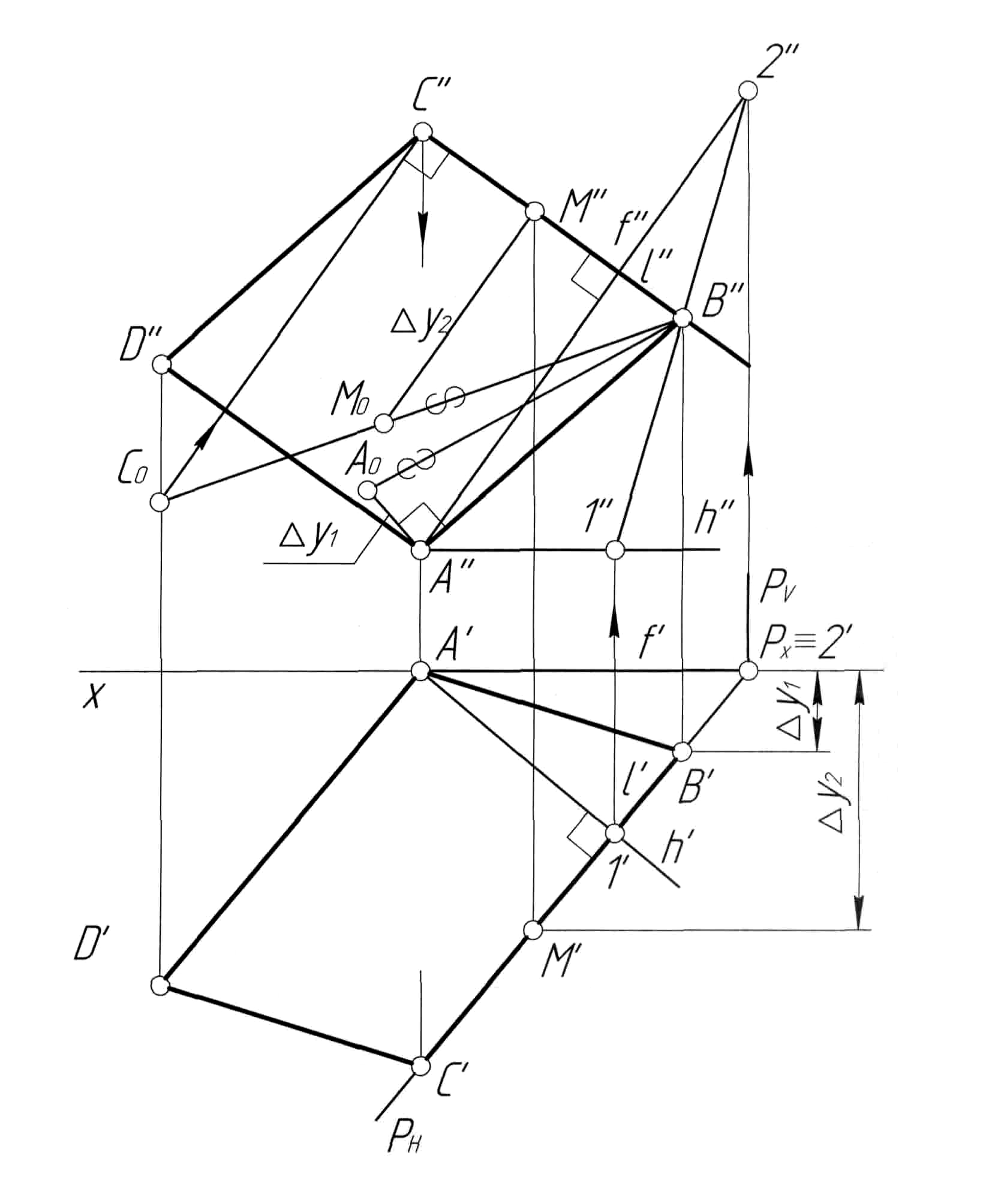
Пример 5.Определить расстояние от точкиDдо плоскостиР, заданной следами (рис. 5,а).

Решение.Расстояние от точки до плоскости определяется длиной отрезка перпендикуляра, опущенного из точки на заданную плоскость. Поэтому решение задачи производим в следующей последовательности (рис. 5, б):

1) из точки Dопускаем на плоскостьРперпендикулярl. Для этого через точкуD''проводим прямуюl''перпендикулярно следуP_V, а через точкуD'проводим прямуюl'перпендикулярно следуP_Н;

2) определяем точку K(K',K'') основания перпендикуляра как точку пересечения прямой lс плоскостьюР(см. пример 3);

3) определяем натуральную величину отрезка перпендикуляра DK (D'K', D''K'') методом прямоугольного треугольника как гипотенузу прямоугольного треугольника, одним из катетов которого является проекция отрезка на плоскость проекций (например, D''K''), а другим – разность расстояний от концов отрезка до той же плоскости проекций (в нашем примере – y).

Построенный отрезок D₀K''и определяет расстояние от точкиDдо плоскостиР.

а)	б)
Рис. 5

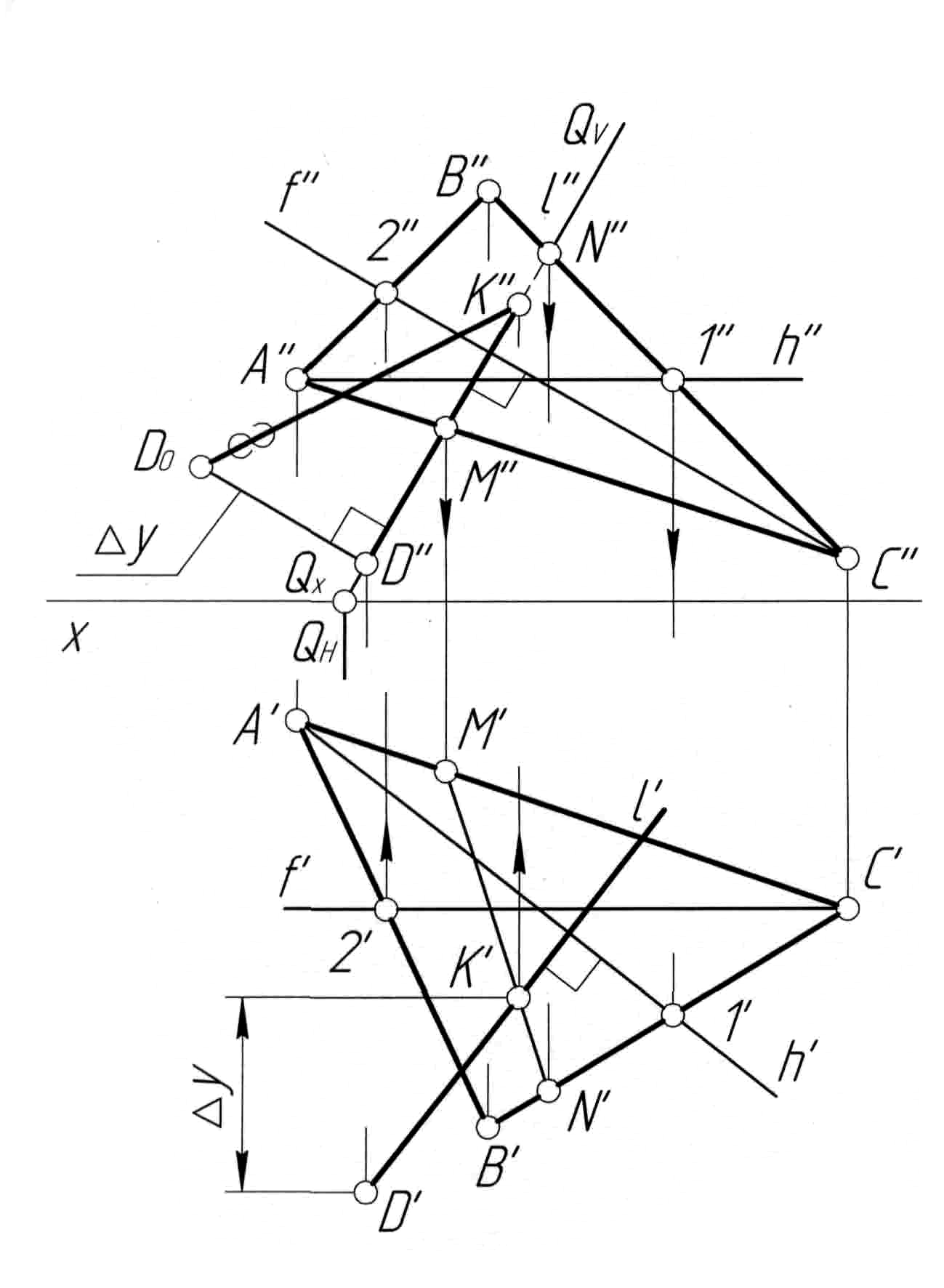
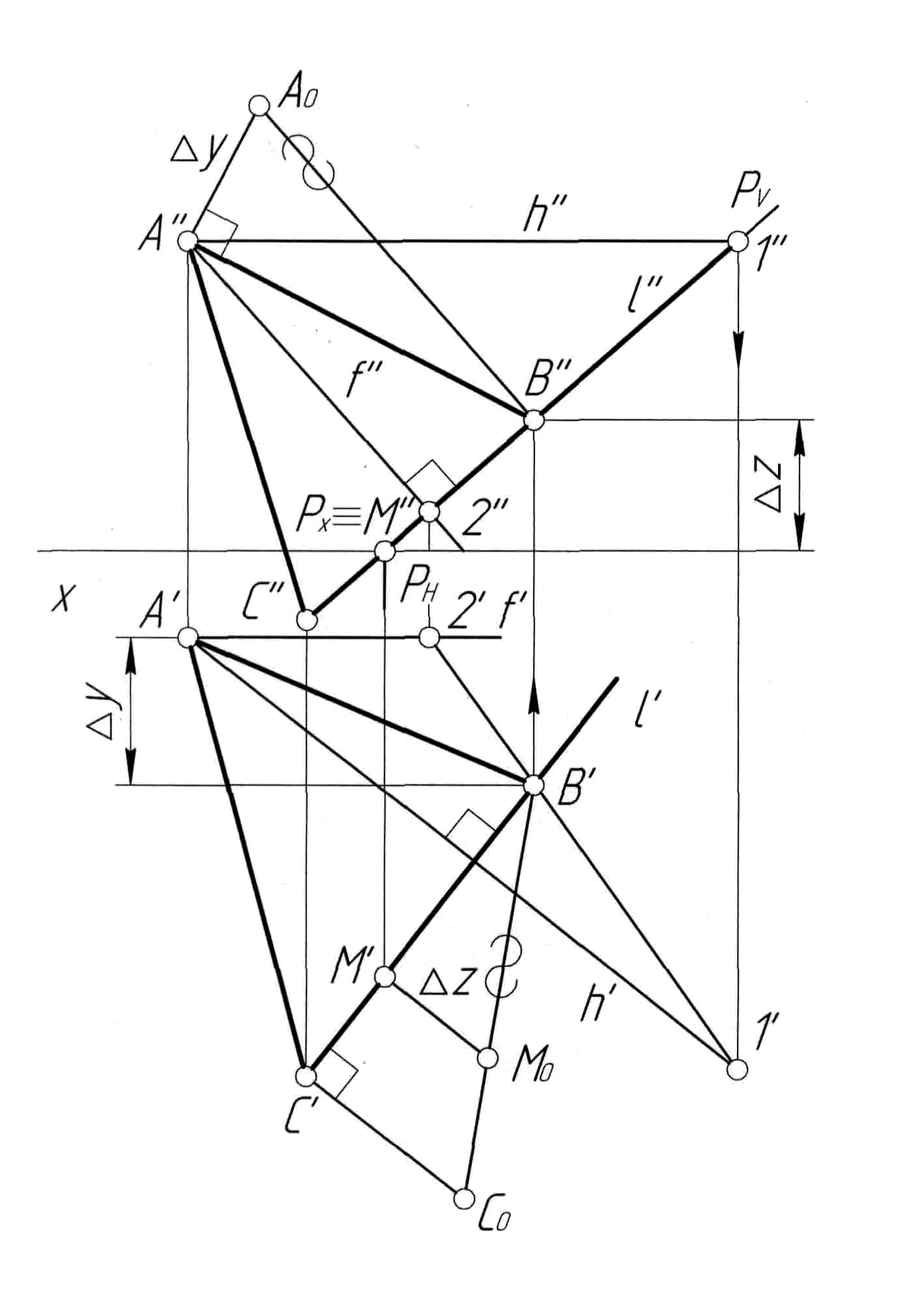
Пример 6.Определить расстояние от точкиDдо плоскости, заданной треугольникомABC(рис. 6,а).

Решение.Решение задачи (рис. 6,б) проводим в последовательности, аналогичной примеру 5. Для построения перпендикуляраl, опущенного из точкиDна плоскость треугольникаABC, в плоскости проводим горизонтальh(h',h'') и фронтальf(f',f''). Далее через точкуD''проводим прямуюl''перпендикулярноf'', а через точкуD'строимl'перпендикулярноh'. Затем строим точкуKпересечения прямойlс плоскостью треугольникаABC(см. пример 4) и находим натуральную величину отрезкаDK(D'K',D''K'') методом прямоугольного треугольника (см. пример 5).

а)	б)
Рис. 6

Параллельность прямой и плоскости.Если прямая параллельна прямой, лежащей в заданной плоскости, то она параллельна и самой плоскости. Для того чтобы проверить, параллельна ли прямая заданной плоскости, можно поступить одним из двух следующих способов:

1) в плоскости проводят прямую, параллельную заданной. Если такую прямую в плоскости подобрать не удается, значит прямая и плоскость не параллельны;

2) строят точку пересечения заданной прямой с плоскостью. Если такая точка не может быть найдена, то прямая и плоскость параллельны.

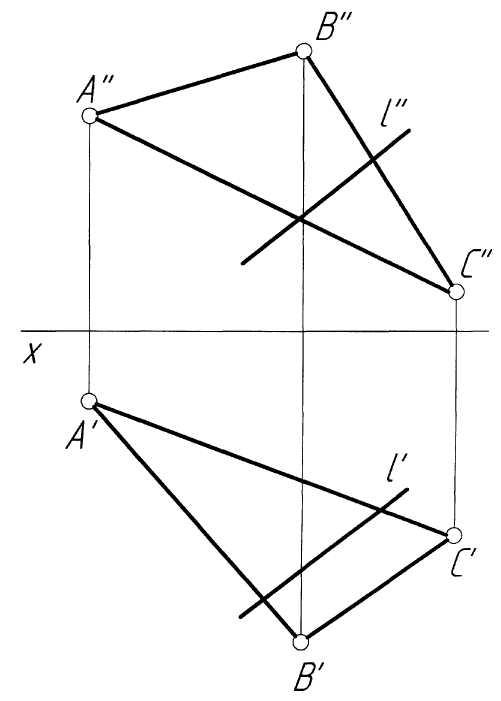
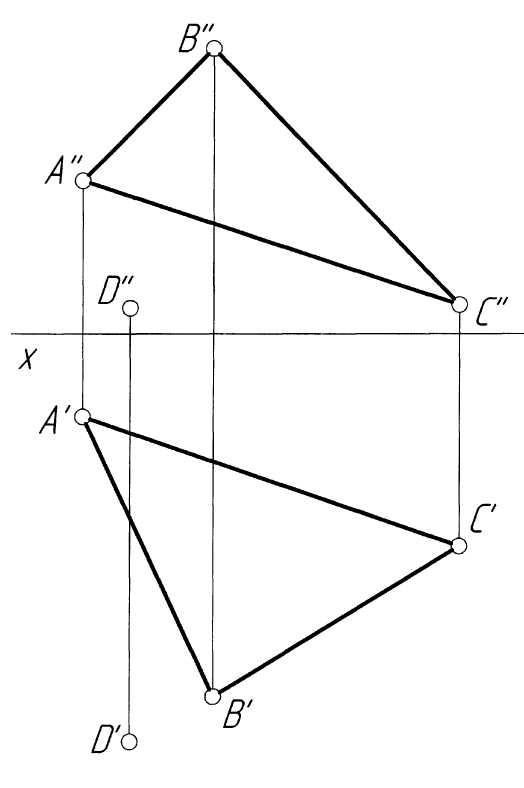
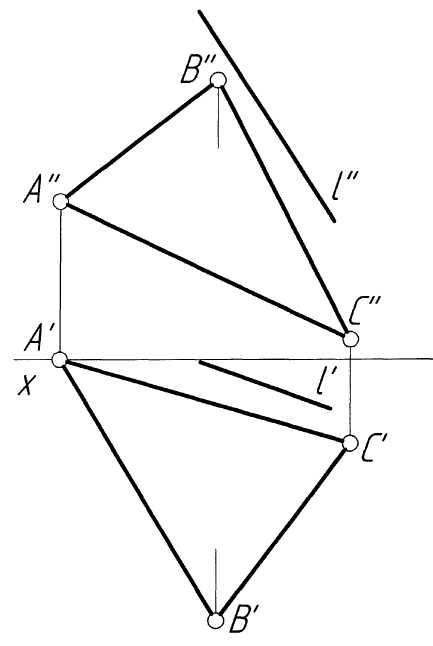
Пример 7.Провести через точкуKпрямую, параллельную плоскости, заданной треугольникомABC(рис. 7,а).

Решение. Для того чтобы построить прямую, проходящую через заданную точку параллельно заданной плоскости, необходимо провести через эту точку прямую, параллельную какой-либо прямой, принадлежащей плоскости треугольника. Известно, что таких прямых может быть бесчисленное множество. На рис. 7, б прямая l параллельна стороне АВ треугольника АВС, и поэтому параллельна плоскости. На рис.7, в прямая l параллельна горизонтали h плоскости треугольника АВС и поэтому также параллельна заданной плоскости.

а)	б)	в)
Рис. 7

Пересечение плоскостей. Две плоскости пересекаются по прямой линии. Поскольку положение прямой в пространстве определяют две точки, то для построения линии пересечения двух плоскостей необходимо и достаточно знать две точки, принадлежащие одновременно каждой из них.

Для нахождения каждой из таких двух точек обычно приходится выполнять специальные построения. Но если хотя бы одна из пересекающихся плоскостей перпендикулярна к одной или двум плоскостям проекций, то построение проекций линии пересечения упрощается.

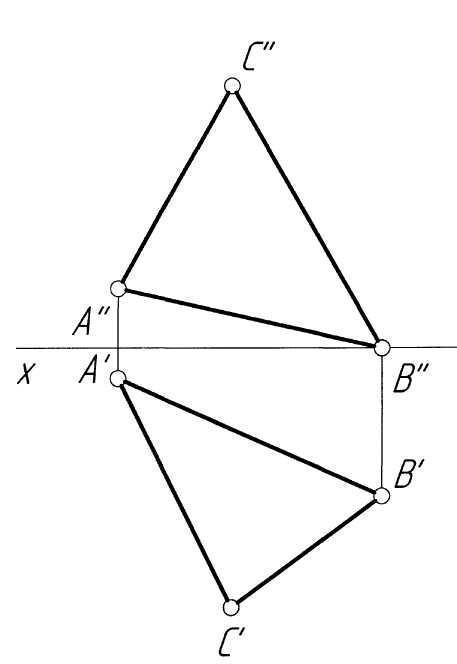
Пример 8. Построить проекции линии пересечения горизонтально-проецирующей плоскостиP, заданной следами, и плоскости треугольникаABC(рис. 8,а).

Решение. Поскольку линияMNпересечения плоскостейPиABCпринадлежит горизонтально-проецирующей плоскости, то ее горизонтальная проекцияM'N'совпадает с горизонтальным следомP_H плоскостиP. Фронтальная проекция линии пересечения пройдет через точкиM'' иN'', расположенные на фронтальных проекцияхA''B''иA''C''соответствующих сторонABиACтреугольника (рис. 8,б).

а)	б)
Рис. 8

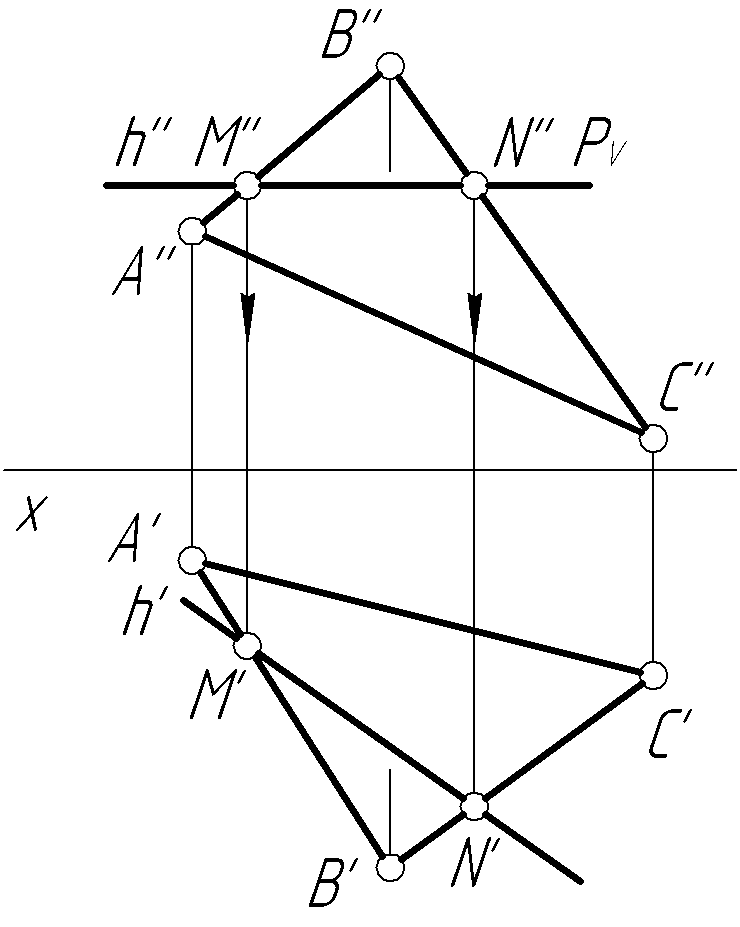
Пример 9. Построить проекции линии пересечения горизонтальной плоскостиP, заданной следами, и плоскости треугольникаABC(рис. 9,а).

Решение. Поскольку одна из пересекающихся плоскостей является горизонтальной, то линией пересечения заданных плоскостей будет горизонталь, проходящая через точки M и N, в которых стороны AВ и BC треугольника АВС пересекаются с плоскостью P (рис. 9, б). Фронтальная проекция M''N'' линии пересечения совпадает с фронтальным следом P_V плоскости P. Горизонтальная проекция пройдет через точки M' и N', расположенные на горизонтальных проекциях A'В' и B'C' соответствующих сторон AВ и BC треугольника.

а)	б)
Рис. 9

Если плоскости заданы следами, то естественно искать точки, определяющие линию их пересечения, в точках пересечения одноименных следов плоскостей. Прямая, проходящая через эти точки, является общей для обеих плоскостей, т.е. их линией пересечения.

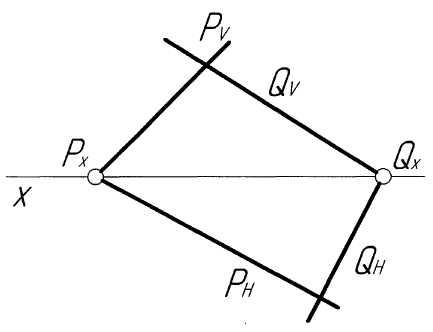
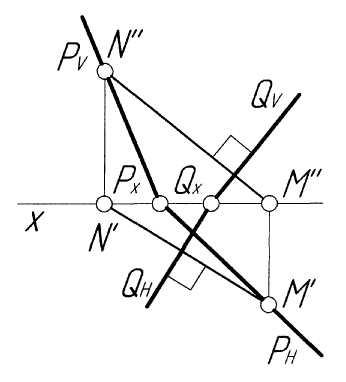
Пример 10. Построить проекции линии пересечения плоскостейPиQ, заданных следами (рис. 10,а).

а)	б)
Рис. 10

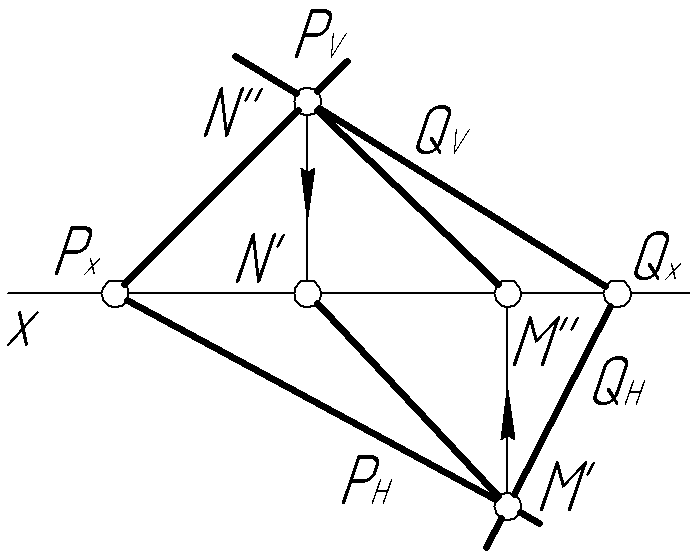
Решение. ЛинияMNпересечения плоскостейPиQпройдет через точки пересечения одноименных следов этих плоскостей. В точкеMпересекаются горизонтальные следыP_H иQ_H, в точкеN– фронтальныеP_V иQ_V. Проекциями линии пересечения будут прямыеM'N'иM''N''(рис. 10,б).

В общем случае линию пересечения двух плоскостей можно найти следующим образом:

1) заданные плоскости пересекают вспомогательными плоскостями;

2) строят линии пересечения вспомогательных плоскостей с заданными;

3) на пересечении построенных линий находят общие для двух заданных плоскостей точки.

Этот способ универсальный и применяется как при построении линии пересечения плоскостей, заданных следами, так и при задании плоскостей любыми другими способами.

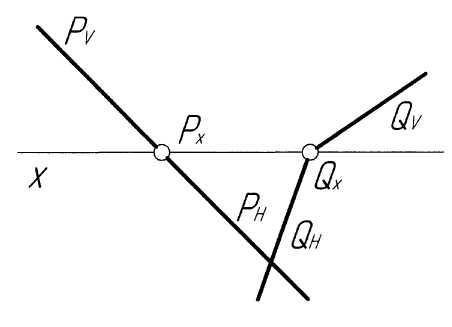
Пример 11. Построить проекции линии пересечения плоскостейPиQ, заданных следами (рис. 11,а).

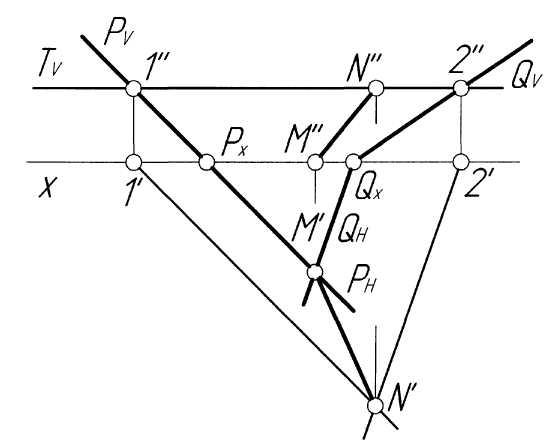
Решение. Первая точка М (M', M''), принадлежащая одновременно обеим плоскостям, строится как точка пересечения горизонтальных следов этих плоскостей (рис. 11, б). Для построения второй точки, принадлежащей линии пересечения, проводим вспомогательную горизонтальную плоскость Т, которая пересекает плоскость Р по горизонтали h₁ (, ), а плоскость Q – по горизонтали h₂ (, ). Пересекаясь между собой и , дают точку N'. Проецируя линию связи на след T_V, получаем точку N''.

а)	б)
Рис. 11

Если хотя бы одна из пересекающихся плоскостей задана не следами, то точки, определяющие линию их пересечения, могут быть найдены как точки пересечения двух каких-либо прямых, принадлежащих одной плоскости с другой плоскостью.

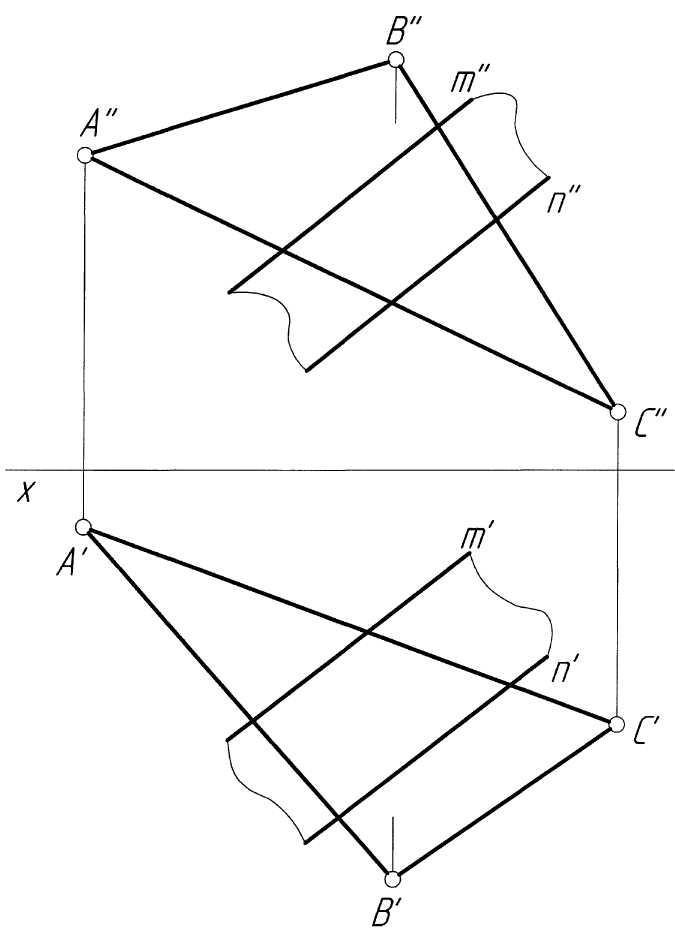
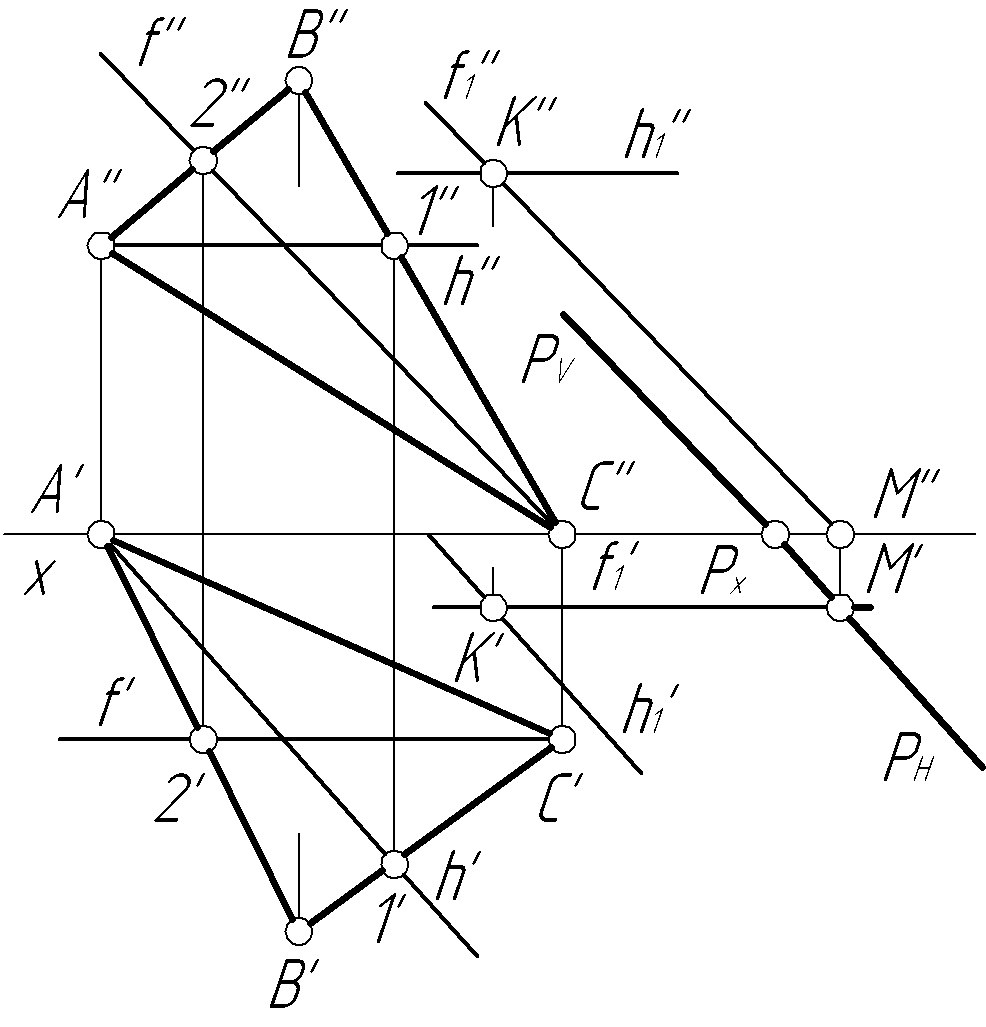
Пример 12. Построить проекции линии пересечения плоскостей общего положения, заданных треугольникомABCи двумя параллельными прямымиmиn(рис. 12,а).

Решение. Решим поставленную задачу двумя способами.

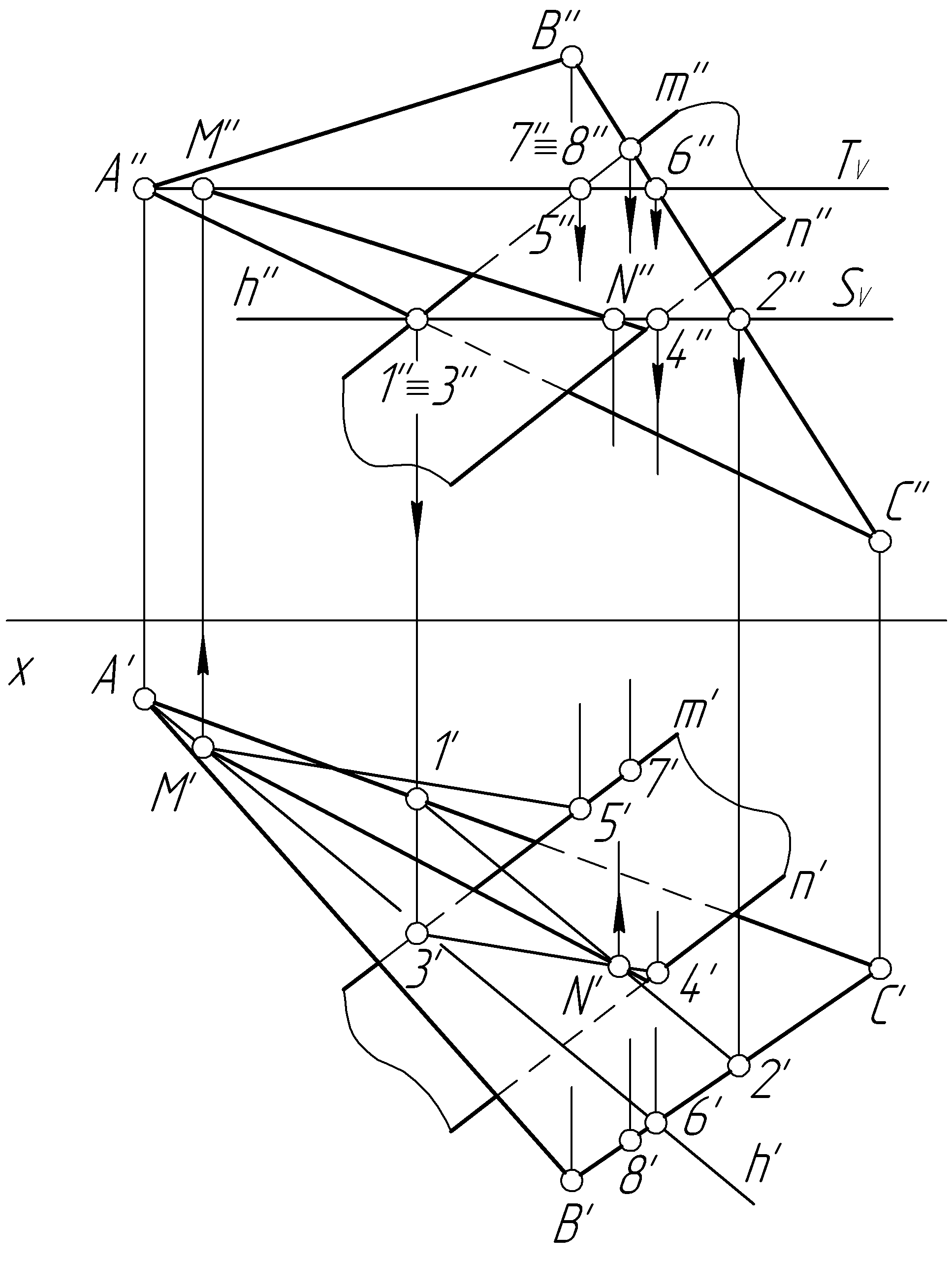
Первый способ(рис. 12,б).Проведем две вспомогательные горизонтальные плоскости S и Т, задав их следами S_V и Т_V. Плоскость S пересекает плоскость треугольника по прямой 12, плоскость, заданную двумя параллельными прямыми, – по прямой 34. По фронтальным проекциям 1''2'' и 3''4'' находим горизонтальные проекции 1'2' и 3'4'. Пересекаясь между собой проекции 1'2' и 3'4' определяют проекцию M' точки M, принадлежащей искомой линии пересечения плоскостей. Cтроим фронтальную проекцию M'' на следе S_V. Вспомогательные

плоскости S и Т параллельны, поэтому линии их пересечения с заданными плоскостями также должны быть параллельны. Проведем горизонтальные проекции линий пересечения плоскости Т с заданными плоскостями через точку А' параллельно 1'2' и через 5' параллельно 3'4'. При пересечении этих прямых определяется проекция N' второй точки N, принадлежащей линии пересечении, по которой строимN''на следеТ_V. Через одноименные проекции точекMиNпроводим проекции линии пересечения плоскостей.

а)	б)

Рис. 12

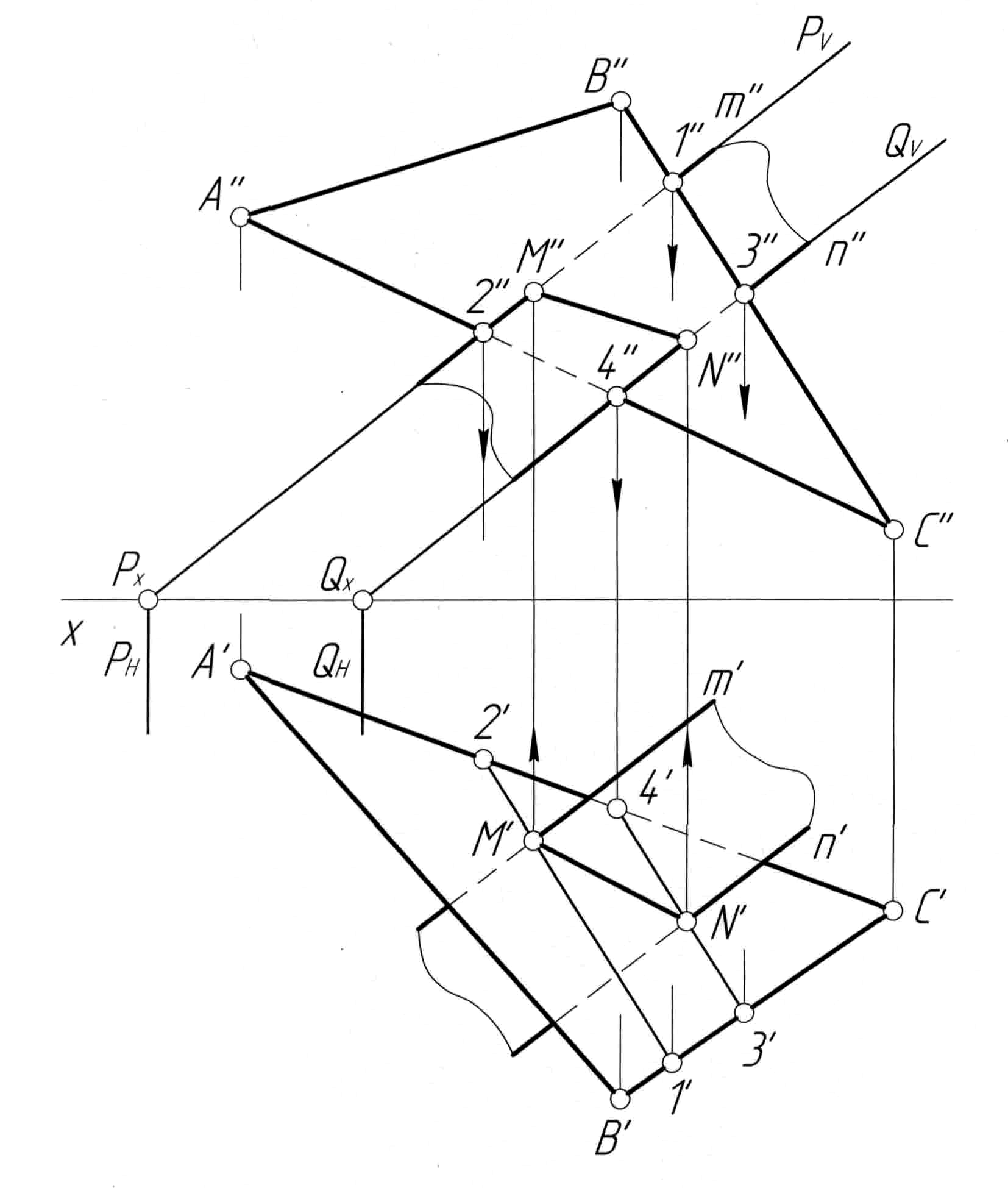
Второй способ(рис. 12,в). Заключаем прямуюm(m',m'') во фронтально-проецирующую плоскостьP, которая пересекает сторонуAC(A'C',A''C'') треугольникаABCв точке1(1',1''), а сторонуBC (B'C',B''C'') – в точке2(2',2''). Прямая12(1'2',1''2'') является линией пересечения плоскости треугольникаАВСс плоскостьюP. Там, где прямая1'2'пересечет прямуюA'C', получаем проекциюM' точкиM, принадлежащей линии пересечения заданных плоскостей. Аналогично, заключая прямуюnво фронтально-проецирующую плоскостьQ, определяем вторую точкуN(N',N''), принадлежащую линии пересечения. Через найденные проекции точекMиNпроводим линию пересеченияMN(M'N',M''N'').

в)

Рис. 12. Продолжение

Видимость элементов чертежа определяем по методу конкурирующих точек (рис. 12, б). В качестве конкурирующих выбираем точки7и8, принадлежащие двум скрещивающимся прямымm и BCсоответственно, проекции7''и8''которых совпадают. Поскольку8'лежит дальше от оси проекций, то прямаяВС, которой принадлежит эта точка, расположена ближе к наблюдателю и закрывает на фронтальной проекции прямуюm. Следовательно, плоскость, заданная треугольникомАВС, будет видима на фронтальной проекции правее линии пересечения. За линией пересечения видимость меняется на противоположную. Аналогично определяется видимость элементов пересекающихся плоскостей на горизонтальной проекции.

Необходимо отметить, что при решении задач, рассмотренных в примерах 11 и 12 можно взять и иные вспомогательные плоскости (например, при решении первым способом задачи из примера 12 можно было взять не две горизонтальные плоскости, а две фронтальные или одну горизонтальную и одну фронтальную). Сущность построений при этом не меняется.

Перпендикулярность плоскостей. Плоскости считаются взаимно перпендикулярными, если прямая, принадлежащая одной плоскости, перпендикулярна другой плоскости. Построение взаимно перпендикулярных плоскостей может осуществляться двумя способами:

1) в заданной плоскости строят принадлежащую ей прямую, а затем перпендикулярно этой прямой проводят плоскость;

2) строят прямую, перпендикулярную заданной плоскости, а затем заключают ее в плоскость.

Пример 13. Построить плоскостьQ, перпендикулярную плоскостиР(рис. 13,а).

Решение. Рассмотрим два способа решения поставленной задачи.

Первый способ(рис. 13,б). Строим прямуюMN (M'N',M''N'') , принадлежащую плоскостиP (Р_Н,Р_V). Перпендикулярно этой прямой строим плоскостьQ (Q_Н,Q_V) (задача имеет множество решений).

Второй способ(рис. 13,в). Перпендикулярно заданной плоскостиР(Р_Н,Р_V) проводим прямуюl (l',l''). Строим горизонтальныйM(M',M'') и фронтальныйN(N',N'') следы прямойl, и через ее следы проводим одноименные следы плоскостиQ (Q_Н,Q_V) (задача имеет множество решений).

а)	б)	в)
Рис. 13

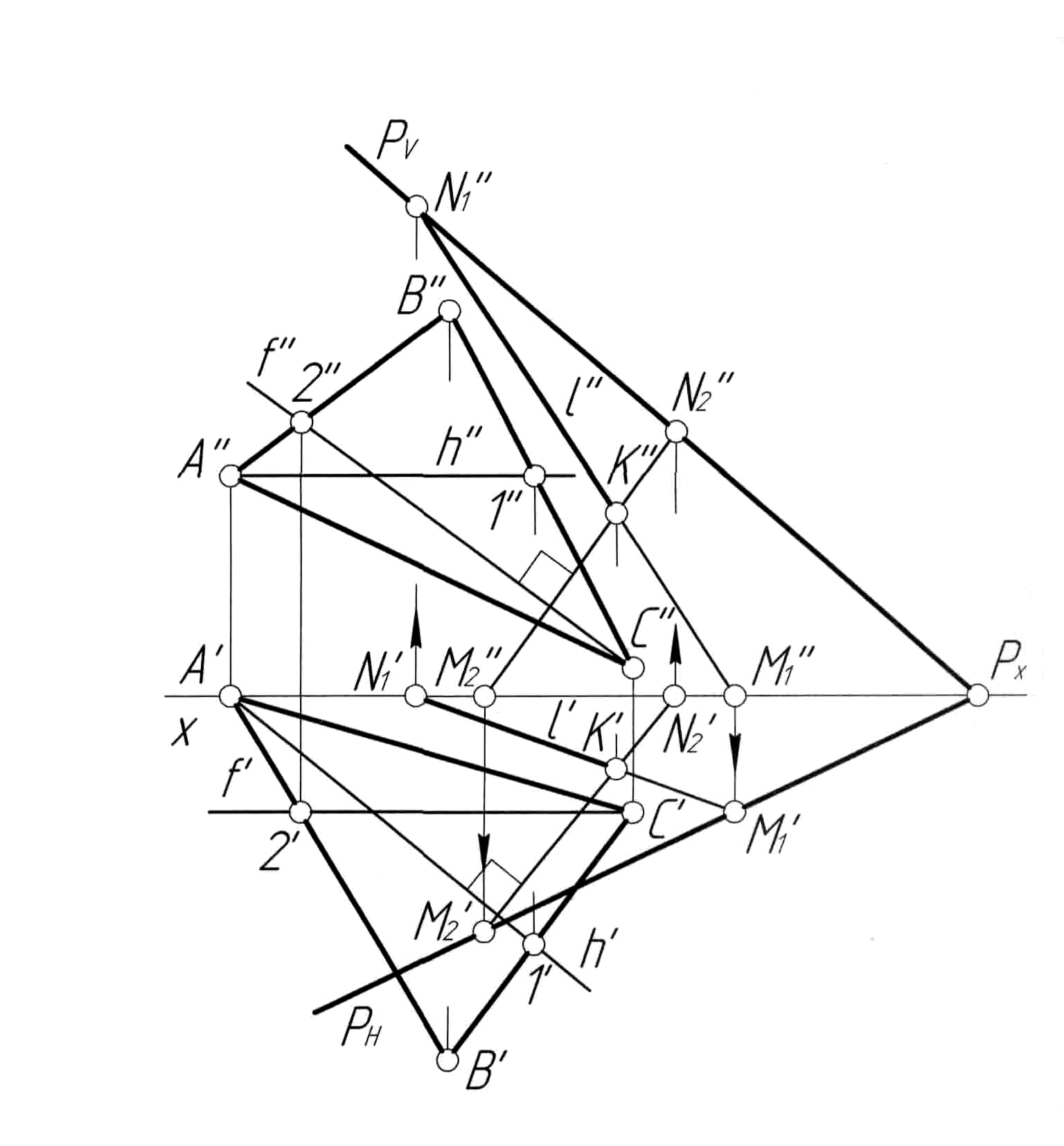
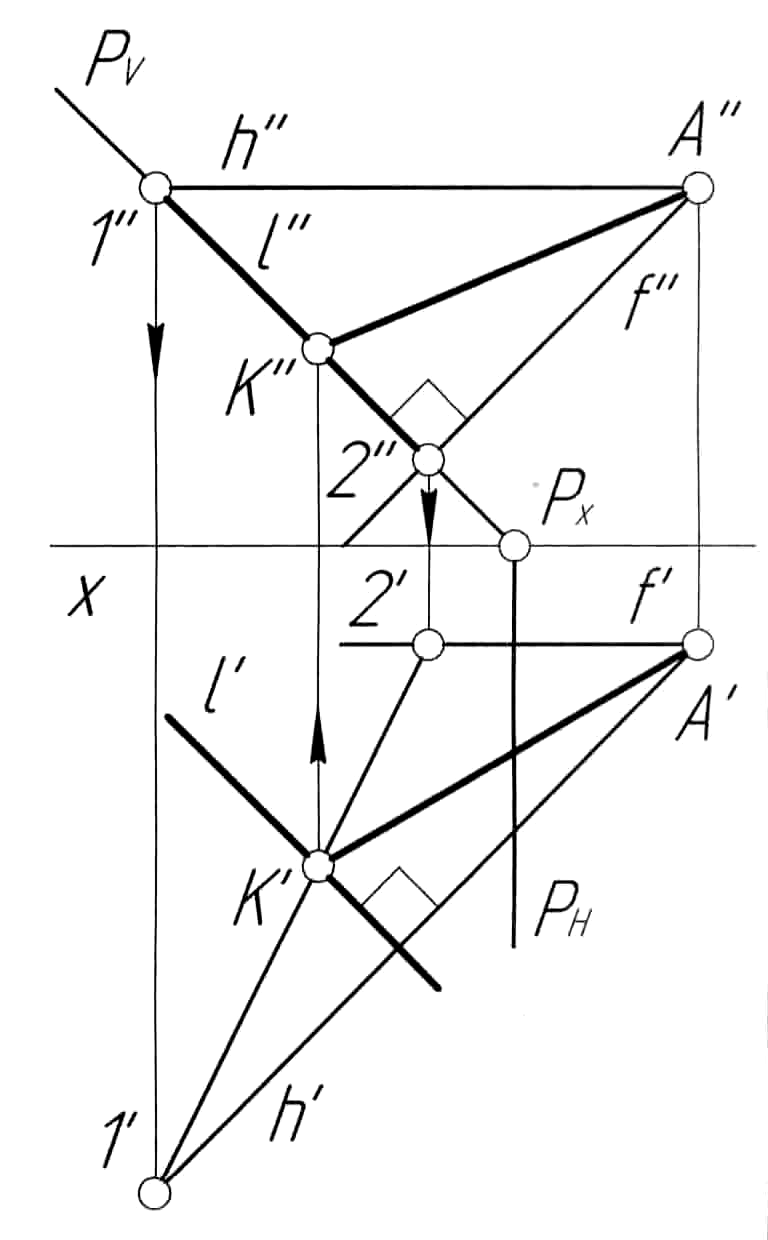
Пример 14. Провести через прямуюl плоскостьР, заданную следами, перпендикулярную плоскости треугольникаABC(рис. 14,а).

Решение. Вначале искомую плоскость зададим двумя пересекающимися прямыми l и n (рис. 14, б). На прямой l (l', l'') берем произвольную точку K (K', K'') и опускаем из нее перпендикуляр n (n', n'') на плоскость треугольника ABC. Для этого в плоскости треугольника проводим горизонталь h (h', h'') и фронталь f (f', f''). Затем из точки K'' опускаем перпендикуляр n'' на f'', а из точки K' опускаем перпендикуляр n' на h'. Пересекающиеся прямые l и n задают плоскость, перпендикулярную плоскости треугольника ABC. Построим следы этой плоскости. Для построения горизонтального следа плоскости найдем горизонтальные M₁ (M₁', M₁'') и M₂ (M₂', M₂'') следы прямых l и n соответственно. Через M₁' и M₂' проводим след Р_Н искомой плоскости Р. Построение следа Р_V аналогично.

а)	б)
Рис. 14

Параллельность плоскостей.Две плоскости считаются параллельными, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Одноименные следы параллельных плоскостей между собой параллельны.

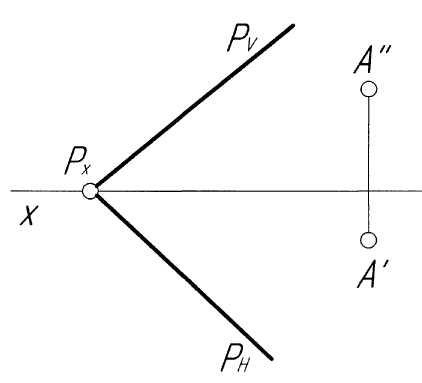
Пример 15. Построить плоскостьQ, проходящую через точкуA, и параллельную плоскостиР(рис. 15,а).

Решение. Через точкуА(А',А'') проведем горизонтальh(h',h'') искомой плоскостиQ, параллельно плоскостиР(рис. 15,б). Фронтальная проекцияh'' этой прямой проходит через точкуА'' и параллельна осиx, а горизонтальная проекция проходит через точкуА'параллельно следуP_Н. Строим фронтальный следN(N',N'') горизонталиh. Следы искомой плоскостиQпроводим следующим образом. Через проекциюN''фронтального следаNгоризонтали параллельноP_Vстроим следQ_Vдо пересечения его с осьюx. Полученная на оси проекций точкаQ_x– точка схода следов. Через точку схода следовQ_x проводим следQ_Нпараллельно следуР_Н. Для построения плоскостиQвместо горизонтали можно использовать фронталь. При этом построения – аналогичны.

Пример 16. Построить плоскостьРследами, проходящую через точкуKи параллельную плоскости треугольникаABC(рис. 16,а).

а)	б)
Рис. 15

Решение. Вначале искомую плоскость зададим двумя пересекающимися прямымиh₁(h₁',h₁'') иf₁(f₁',f₁''), проходящими через точкуK(K',K'') и параллельными горизонталиh(h',h'') и фронталиf(f',f'') плоскости треугольникаАВСсоответственно (рис. 16,б). Далее найдем горизонтальный следМ(М',М'') фронталиf₁(f₁',f₁'') искомой плоскости и проведем через него следР_Нпараллельно проекцииh₁'горизонтали до пересечения с осью проекций. Полученная на оси точкаР_x– точка схода следов. Через эту точку строим следP_V параллельно проекцииf₁''фронтали.

а)	б)
Рис. 16

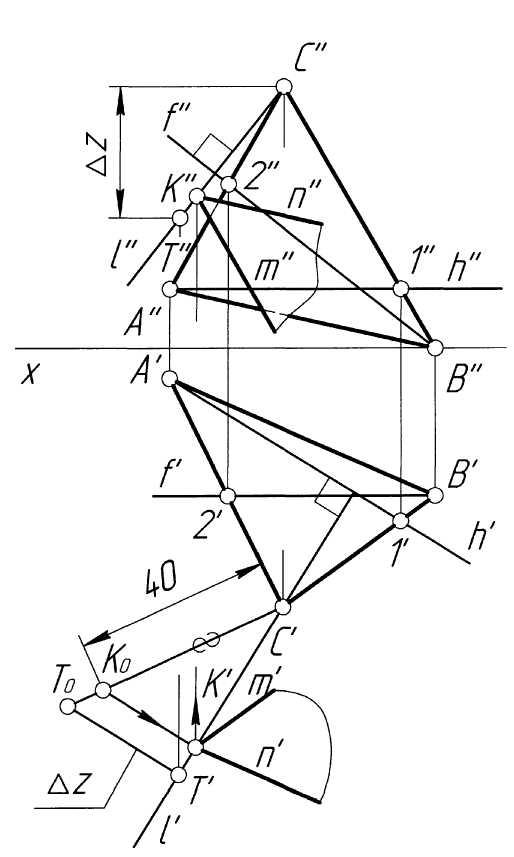
Пример 17. Построить плоскость, заданную двумя пересекающимися прямымиmиn(отсеком), параллельную плоскости треугольникаABCи отстоящую от нее на расстояние 40 мм (рис. 17, а).

Решение. Через любую точку в плоскости треугольника АВС, например, вершину С (C', C''), проводим прямую, перпендикулярную этой плоскости. Для этого строим в плоскости АВС горизонталь h (h', h'') и фронталь f (f', f''). Далее через точку С'' перпендикулярно f'' проводим проекцию l'', а через С' перпендикулярно h' проводим l'. Выбираем на прямой l произвольную точку Т (Т', Т'') и определяем натуральную величину отрезка CТ (С'Т', С''Т''), вдоль которой от точки С откладываем 40 мм и получаем точку K. Находим проекции точки K (K', K'') на прямой l (l', l''). Далее через точку K (K', K'') проводим две пересекающиеся прямые m (m', m'') и n (n', n''), параллельные двум пересекающимся прямым плоскости треугольника ABC, например, AB (A'B', A''B'') и BC (B'C', B''C'') соответственно (рис. 17, б). Эти прямые и задают искомую плоскость.

а)	б)
Рис. 17

Перпендикулярность прямых общего положения.Построение двух взаимно перпендикулярных прямых общего положения выполняют при помощи плоскости, перпендикулярной к одной из них. Через точку пересечения прямой и перпендикулярной к ней плоскости проводят в плоскости любую прямую, которая и будет перпендикулярна к заданной прямой.

Пример 18.Провести через точкуАпрямую, перпендикулярную прямойlобщего положения (рис.18,а).

а)	б)
Рис. 18

Решение.Решение задачи производим в следующей последовательности (рис. 18,б). Через точкуАпроводим плоскость, перпендикулярную прямойl. Проще всего такую плоскость задать двумя пересекающимися прямыми (отсеком) – горизонтальюh(h',h'') и фронтальюf(f',f''), которые проводим через точкуА, перпендикулярно прямойl. При этом проекциюh'строим перпендикулярноl', а проекциюf'' – перпендикулярноl''. Затем определяем точкуK(K',K'') пересечения прямойlсо вспомогательной плоскостью, заданной горизонталью и фронталью. Для этого заключаем прямуюlво фронтально-проецирующую плоскостьР(Р_Н,Р_V), которая пересекает горизонталь и фронталь в точках1и2соответственно. Проекции1''и2'' этих точек находим на пересечении следаР_Vс фронтальными проекциями горизонтали и фронтали. Затем определяем проекции1'и2'. Прямая12(1'2',1''2'') – линия пересечения плоскостиР(Р_Н,Р_V) с плоскостью, заданной горизонталью и фронталью. На пересечении линии12(1'2',1''2'') с прямойl(l',l'') получаем точкуK(K',K''). Соединяя соответствующие проекции точекА(А',А'') иK(K',K''), получаем проекции прямойAK, перпендикулярной заданной.

Пример 19.Определить расстояние от точкиАдо прямойlобщего положения (рис. 19,а).

Решение. Расстояние от точки до прямой определяется длиной отрезка перпендикуляра, опущенного из точки на эту прямую. Решение задачи (рис. 19, б) аналогично примеру 17. В заключение необходимо определить натуральную величину отрезка АK (А'K', А''K'').

а)	б)
Рис. 19

Пример 20.Построить проекции равнобедренного прямоугольного треугольникаABCсо сторонойBCна прямойl(рис. 20,а).

Решение.КатетомABпрямоугольного треугольникаABCявляется отрезок перпендикуляра, опущенного из точкиAна прямуюl. Проводим из точкиАпрямую, перпендикулярную прямойl(рис. 20,б), и находим натуральную величину отрезкаAB(см. примеры 18 и 19). Поскольку треугольникABCпо условию равнобедренный, а следовательно,AB=BC, то для нахождения проекций точкиС (С',С'') необходимо натуральную величину отрезкаАВ(А'В',А''В'') отложить на натуральной величине произвольного отрезкаВМ(В'М',В''М'') прямойl. В заключение соединяем одноименные проекции точекА,ВиСи получаем проекции искомого треугольникаАВС.

а)	б)
Рис. 20

Пример 21.Построить проекции прямоугольникаABCDсо сторонойBCна прямойl, еслиАВ:ВС= 2 : 3 (рис. 21,а).

Решение.СторонойABпрямоугольникаABCDявляется отрезок перпендикуляра, опущенного из точкиAна прямуюl. Проводим из точкиАпрямую, перпендикулярную прямойl(рис. 21,б), и находим натуральную величину отрезкаAB(см. примеры 18 и 19). Поскольку стороны прямоугольникаABCDпо условию связаны соотношениемАВ:ВС= 2 : 3, то есть сторонаВСв 1,5 раза большеAB, то для нахождения проекций точкиС (С',С'') необходимо вдоль натуральной величины произвольного отрезкаВМ(В'М',В''М'') прямойlотложить отрезок, длина которого в 1,5 раза больше, чем натуральная величина отрезкаАВ(А'В',А''В''). Для построения точкиD (D',D'') через точкиА (А',А'') иС (С',С'') проводим прямые, параллельныеВС(В'С',В''С'') иАВ(А'В',А''В'') соответственно.

а)	б)
Рис. 21