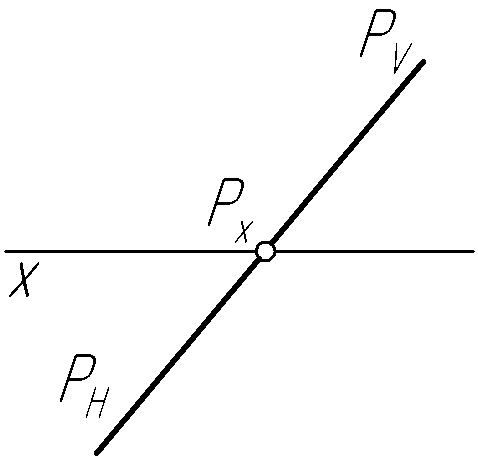
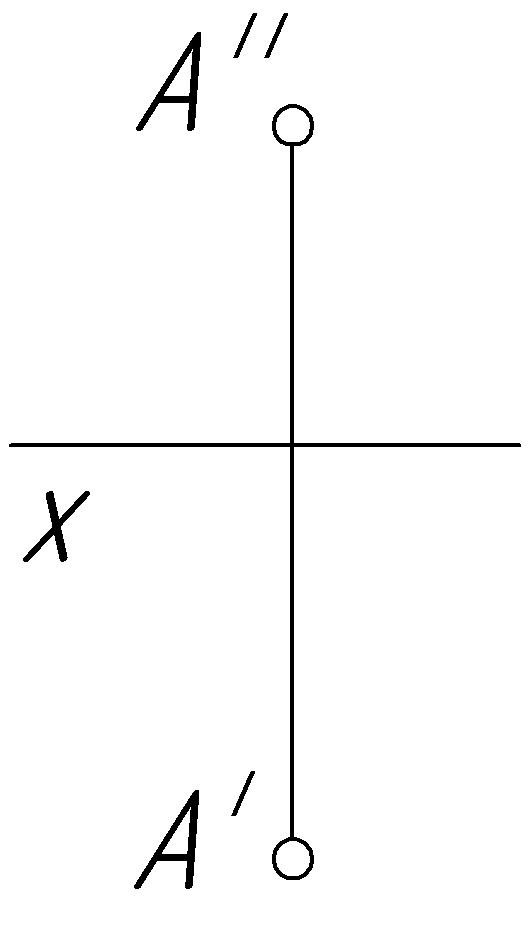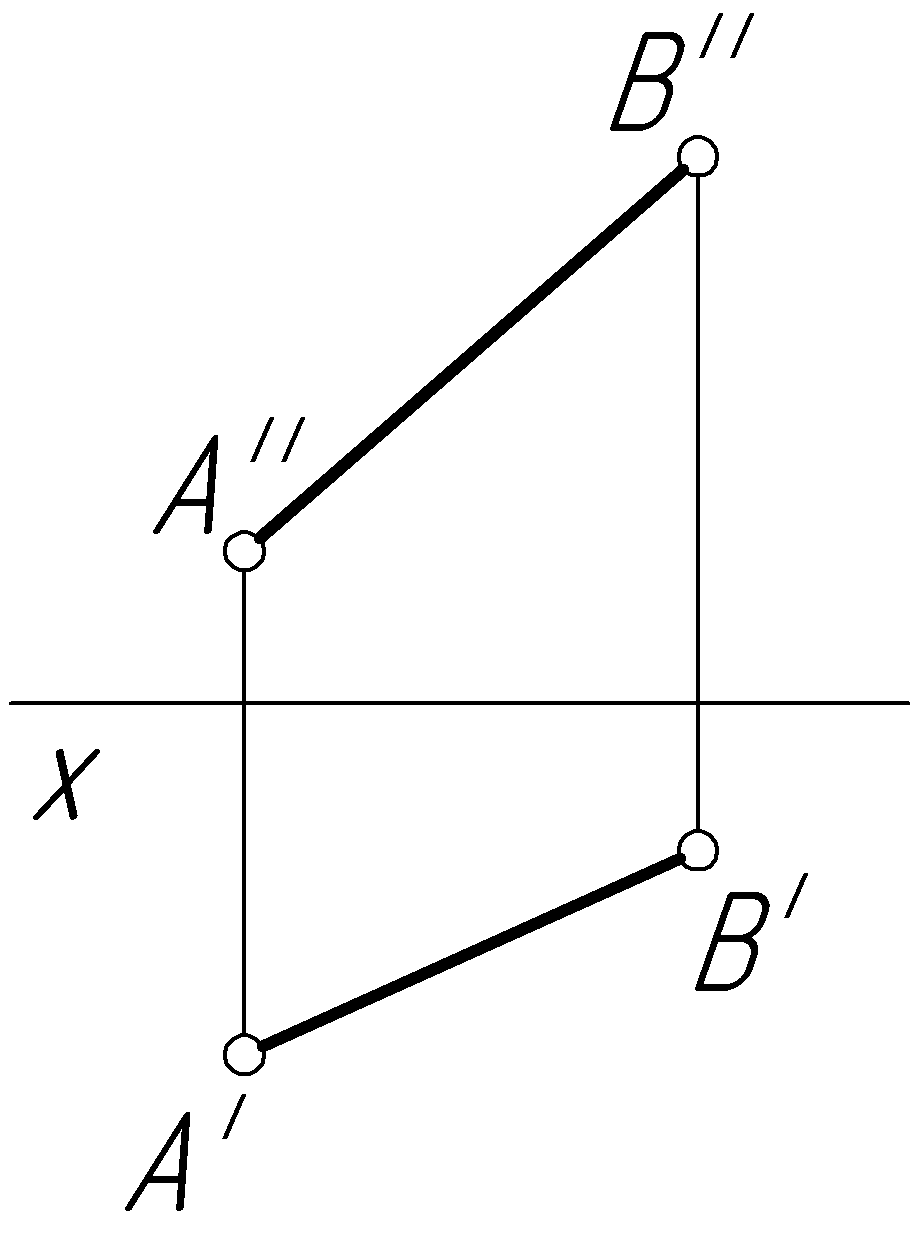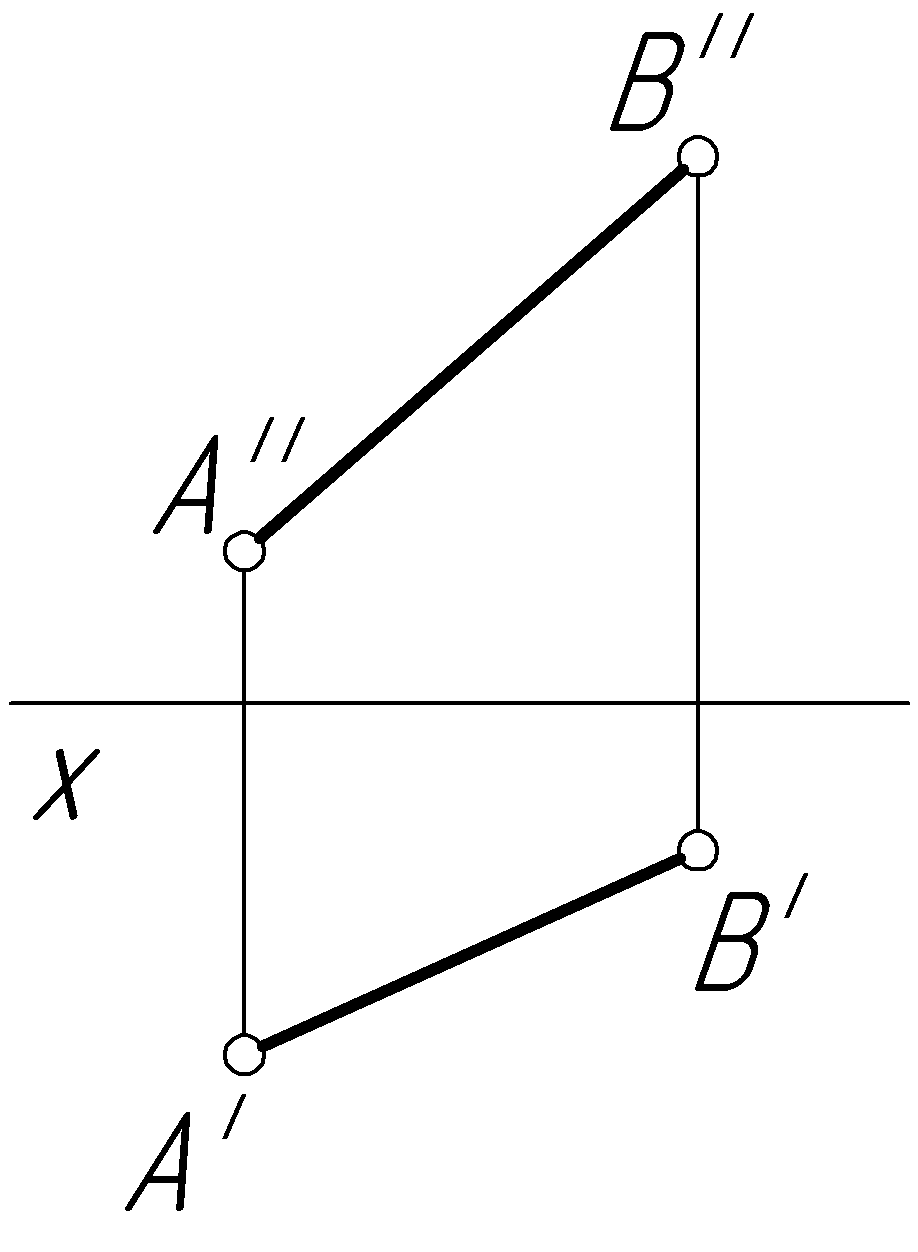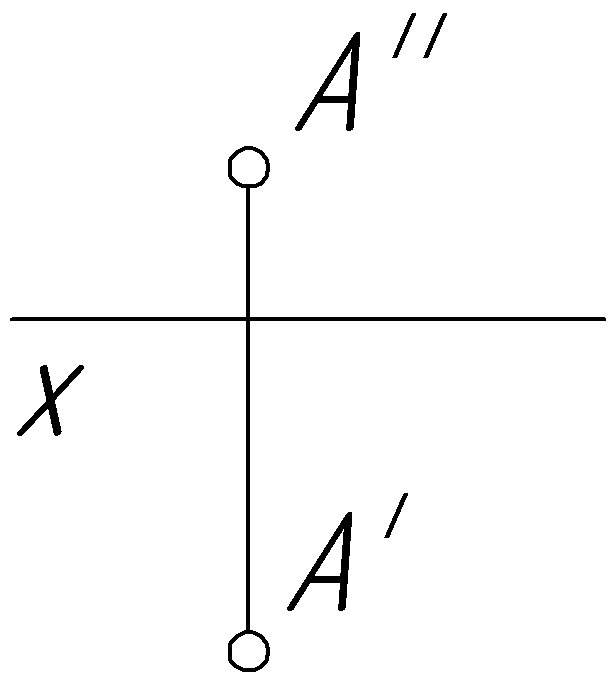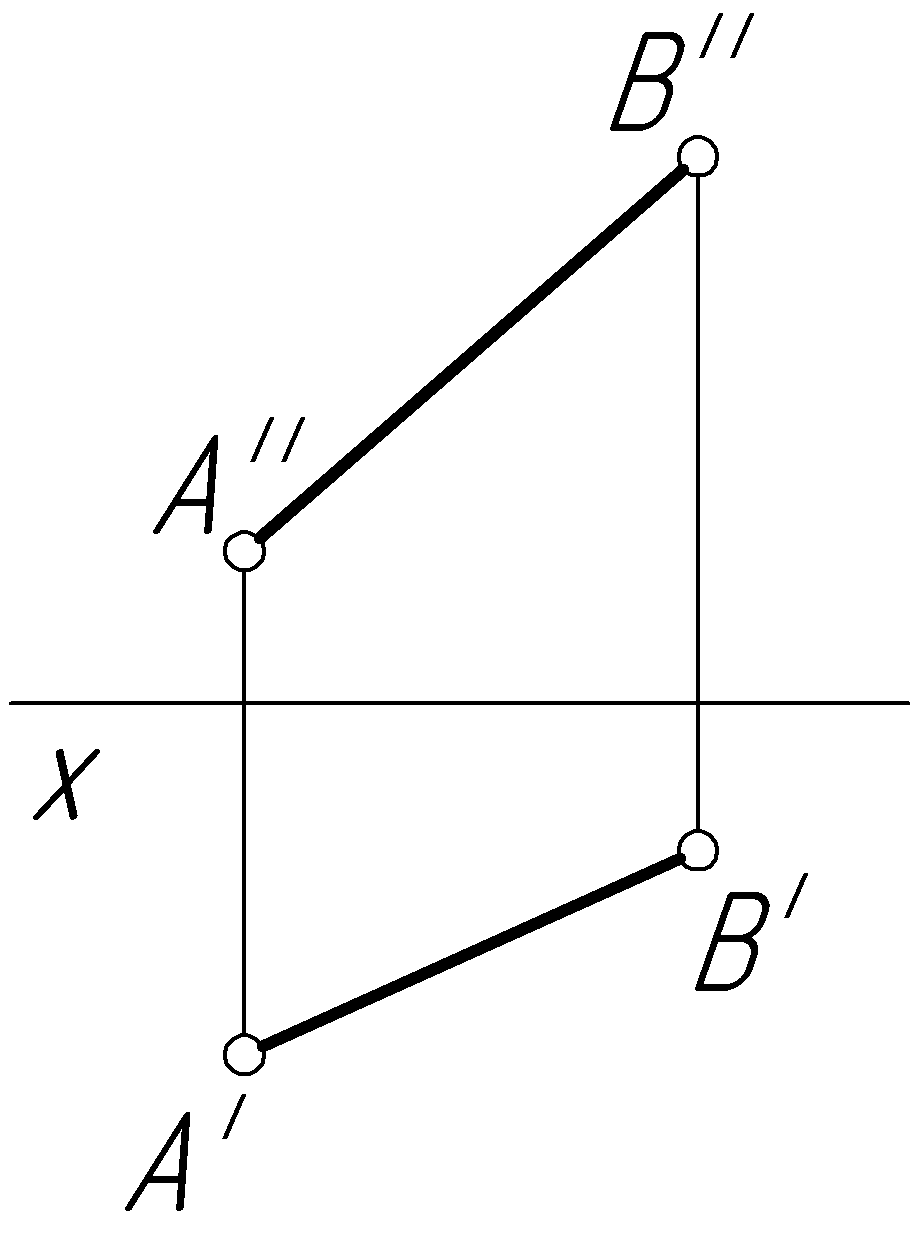- •Принятые обозначения
- •Взаимное положение прямой и плоскости и плоскостей между собой Примеры решения задач
- •Задачи для самостоятельного решения
- •Способы преобразования проекций Примеры решения задач
- •Задачи для самостоятельного решения
- •Пересечение поверхностей плоскостью. Развертывание поверхностей Примеры решения задач
- •Задачи для самостоятельного решения
- •Взаимное пересечение поверхностей Примеры решения задач
- •Задачи для самостоятельного решения
Способы преобразования проекций Примеры решения задач
Способ вращения. Выбрав ось вращения, объекты проецирования (точку, прямую и плоскость) можно повернуть до требуемого частного положения (параллельного или перпендикулярного плоскости проекций). При этом все точки вращаемых объектов перемещаются в параллельных плоскостях по окружностям. Вращение любой точки осуществляется в следующей последовательности:
1) выбирают ось вращения и проводят плоскость, в которой вращается точка. Плоскость вращения всегда должна быть перпендикулярной оси вращения;
2) определяют центр и радиус (его натуральную величину) вращения;
3) производят необходимый поворот.
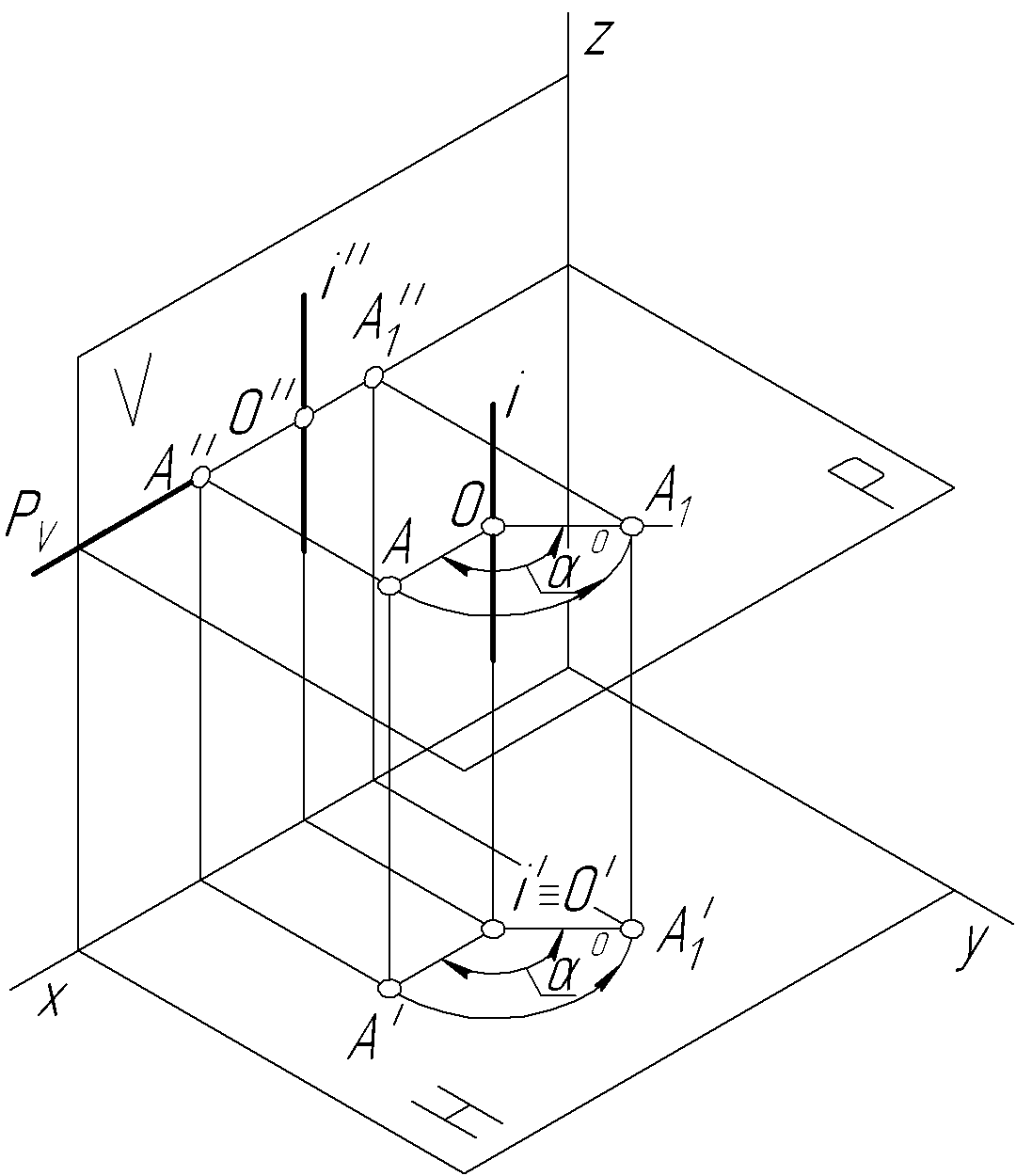
Пример 22.
Повернуть точку А
вокруг горизонтально-проецирующей оси
i
против хода часовой стрелки на угол
![]() (рис. 51,а).
(рис. 51,а).
|
|
|
|
а) |
б) |
в)
Рис. 51
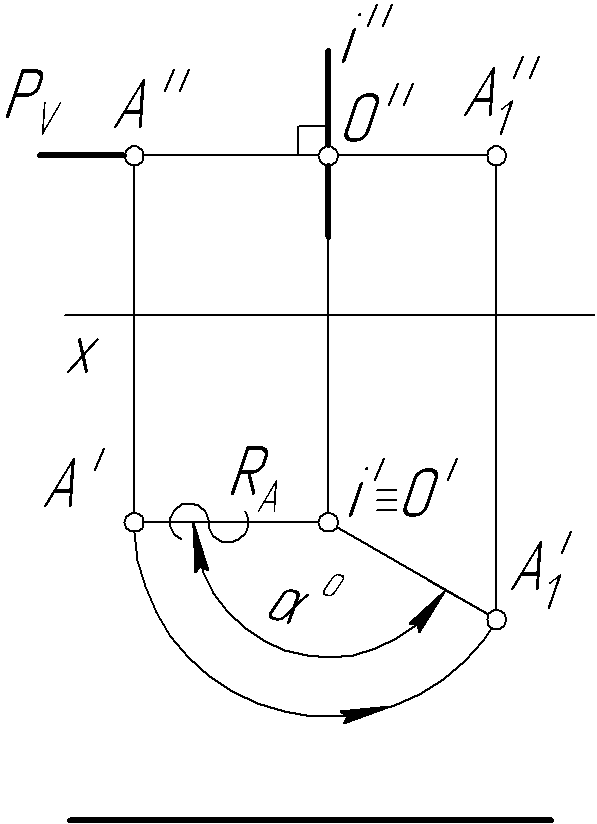
Решение. Точка
А
(А',
А'')
вращается вокруг оси i
в горизонтальной плоскости Р
(![]() )
(рис. 51, б,
в).
Проводим из точки А
(А',
А'')
перпендикуляр АО
(А'О',
А''О'')
к оси вращения. Поскольку АО
(А'О',
А''О'')
является
отрезком горизонтальной прямой, то на
горизонтальную плоскость проекций он
спроецируется в натуральную величину.
Радиусом А'О'
поворачиваем
точку А
(А',
А'')
на заданный угол
)
(рис. 51, б,
в).
Проводим из точки А
(А',
А'')
перпендикуляр АО
(А'О',
А''О'')
к оси вращения. Поскольку АО
(А'О',
А''О'')
является
отрезком горизонтальной прямой, то на
горизонтальную плоскость проекций он
спроецируется в натуральную величину.
Радиусом А'О'
поворачиваем
точку А
(А',
А'')
на заданный угол
![]() .
.
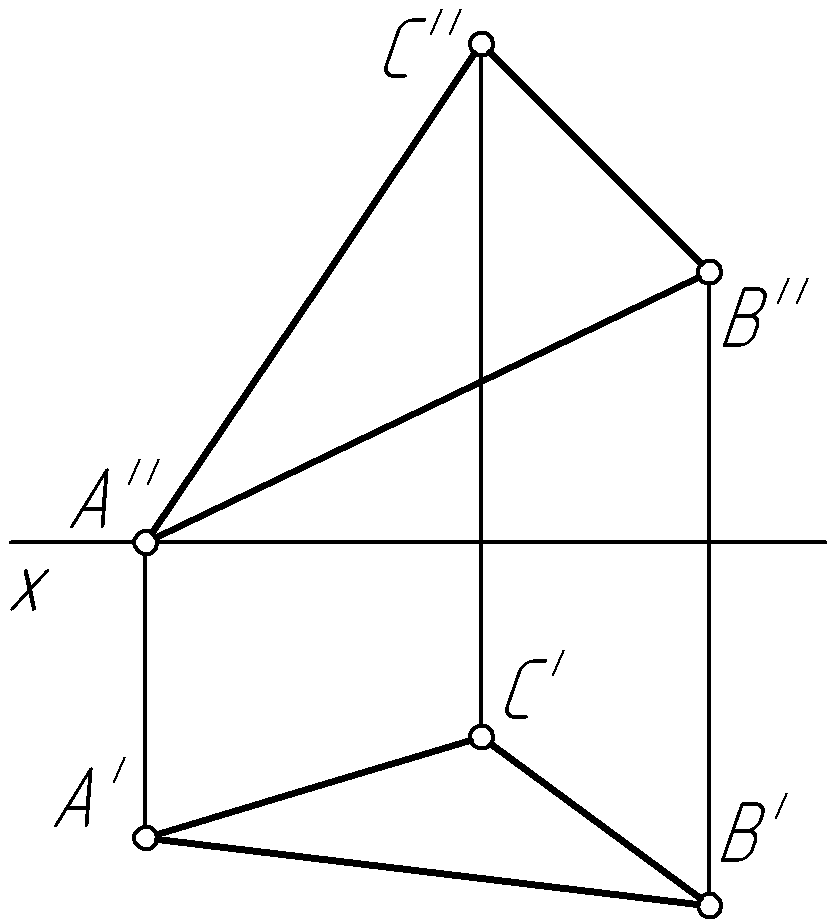
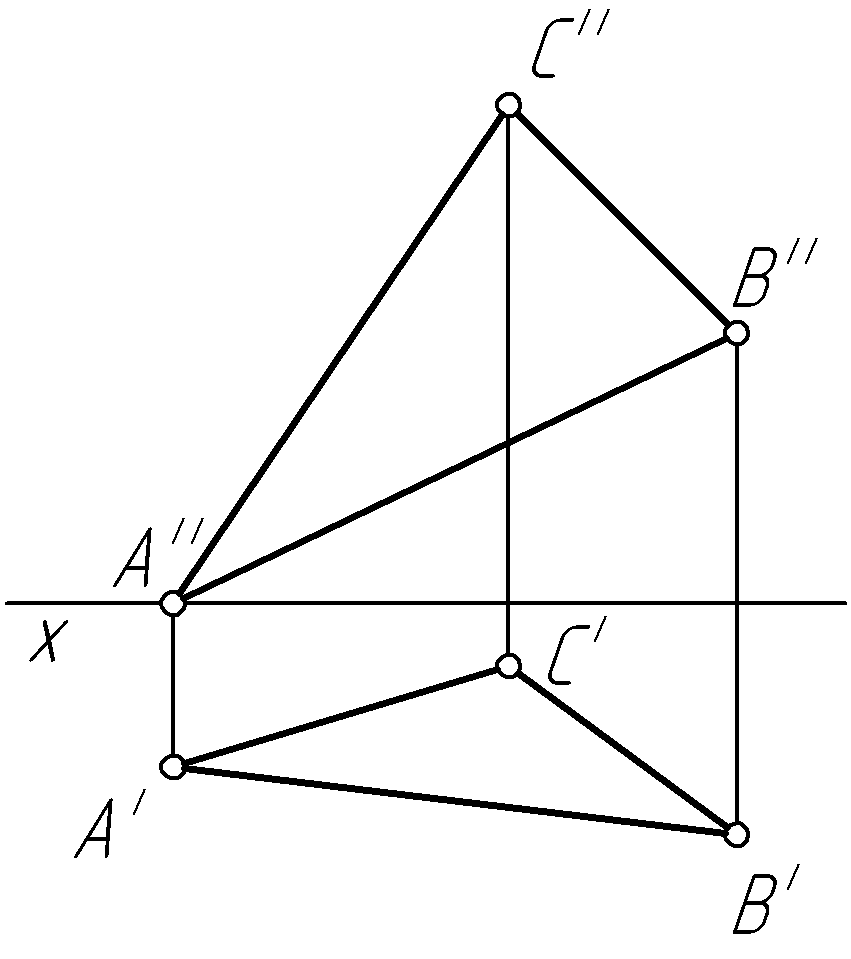
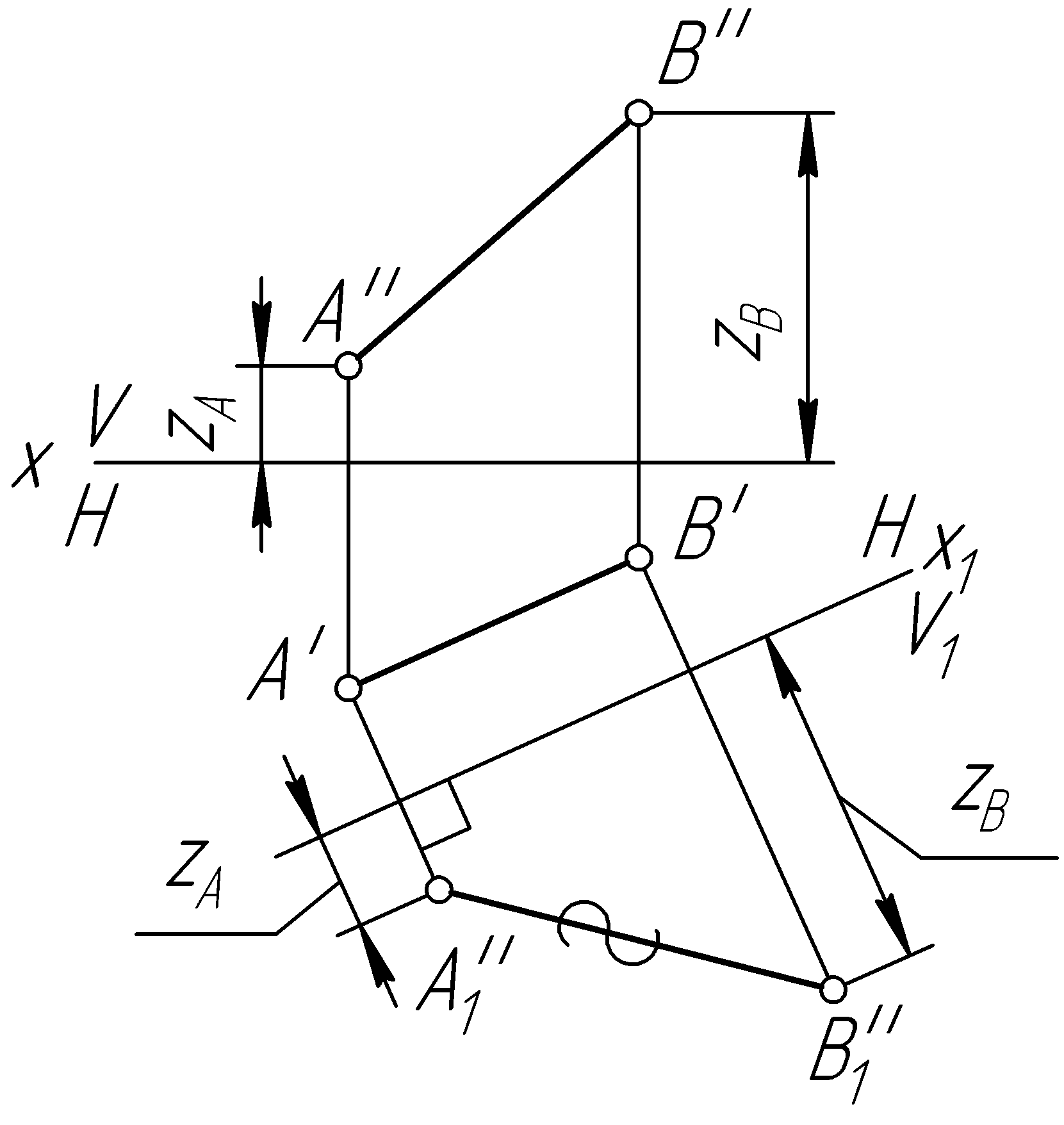
Пример 23. Определить натуральную величину отрезка АВ общего положения (рис. 52, а).
|
|
|
|
а) |
б) |

в)
Рис. 52
Решение.
Для того
чтобы определить натуральную величину
отрезка, его необходимо привести в
положение, параллельное одной из
плоскостей проекций, например, фронтальной
(рис. 52, б).
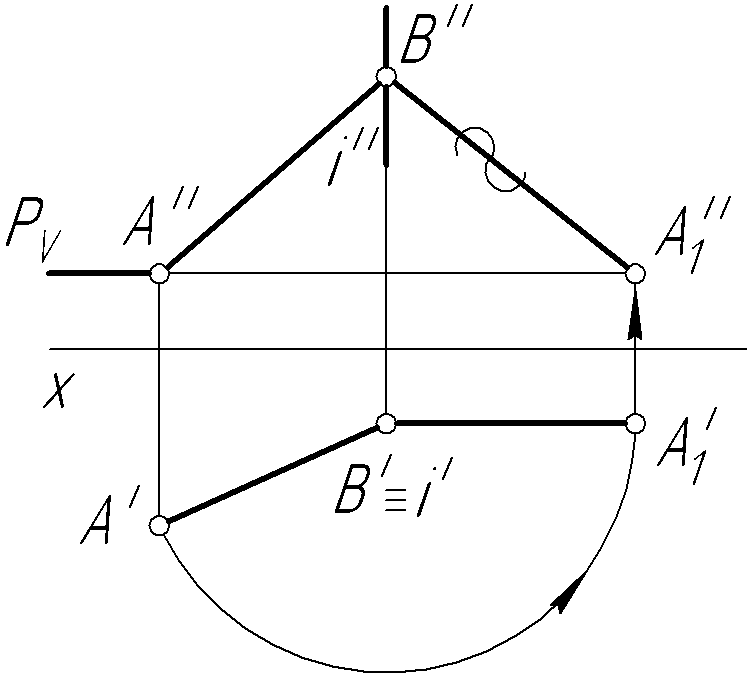
Проводим через точку В
(В',
В'')
горизонтально-проецирующую
ось вращения i
(i',
i'').
Тогда точка В
(В',
В'')
отрезка будет неподвижной, а точка А
(А',
А'')
вращается в горизонтальной плоскости
Р
(![]() )
до тех пор, пока отрезок АВ
(А'В',
А''В'')
не окажется в положении, параллельном
фронтальной плоскости проекций. В этом
положении его горизонтальная проекция
должна быть параллельна оси проекций
(
)
до тех пор, пока отрезок АВ
(А'В',
А''В'')
не окажется в положении, параллельном
фронтальной плоскости проекций. В этом
положении его горизонтальная проекция
должна быть параллельна оси проекций
(![]() В'
║x).
Далее строим проекцию
В'
║x).
Далее строим проекцию
![]() точкиА
в повернутом положении, и, соединяя ее
с В'',
получаем натуральную величину отрезка
АВ.
точкиА
в повернутом положении, и, соединяя ее
с В'',
получаем натуральную величину отрезка
АВ.
Аналогично можно построить натуральную величину отрезка АВ, приведя его в горизонтальное положение, вращением вокруг фронтально-проецирующей прямой (рис. 52, в).
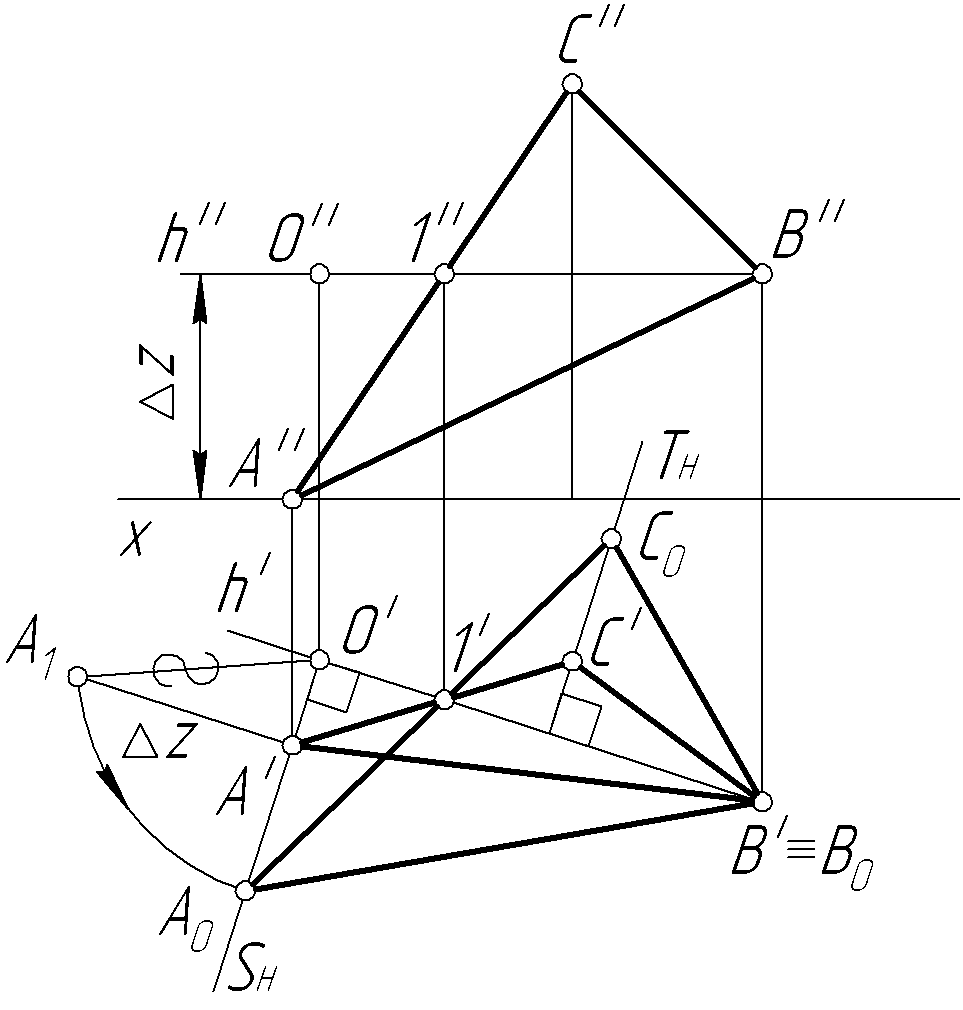
Пример 24. Вращением вокруг линии уровня определить натуральную величину треугольника ABC (рис. 53, а).
Решение. Для построения натуральной величины треугольника необходимо повернуть его плоскость до положения, параллельного одной из плоскостей проекций. На рис. 53, б показано вращение плоскости треугольника ABC вокруг его горизонтали h до положения, параллельного горизонтальной плоскости проекций.
|
|
|
|
а) |
б) |
Рис. 53
Решение выполняется
в следующей последовательности. В
плоскости треугольника ABC
проводим горизонталь h
(![]() ,
,![]() ).
Затем строим следы
).
Затем строим следы![]() и
и![]() горизонтально-проецирующих плоскостей
горизонтально-проецирующих плоскостей![]() и
и![]() ,
в которых вращаются точкиA
и C
соответственно, перпендикулярно
горизонтали h
(
,
в которых вращаются точкиA
и C
соответственно, перпендикулярно
горизонтали h
(![]()
![]()
![]() и
и![]()
![]()
![]() ).
ТочкаВ
неподвижна, так как лежит на оси вращения
(горизонтали h).
Определяем центр и натуральную величину
радиуса вращения точки A.
Центром вращения является точка
О (
).
ТочкаВ
неподвижна, так как лежит на оси вращения
(горизонтали h).
Определяем центр и натуральную величину
радиуса вращения точки A.
Центром вращения является точка
О (![]() ,
,![]() ).
Натуральная величина
).
Натуральная величина![]() отрезкаАО
определена способом прямоугольного
треугольника. Далее от точки
отрезкаАО
определена способом прямоугольного
треугольника. Далее от точки
![]() откладываем по следу
откладываем по следу![]() отрезок
отрезок![]() и получаем положение вершиныА
после поворота. Для построения точки
и получаем положение вершиныА
после поворота. Для построения точки
![]() через точку
через точку![]() и точку
и точку![]() (она также неподвижна, поскольку лежит
на оси вращенияh)
проводим прямую
(она также неподвижна, поскольку лежит
на оси вращенияh)
проводим прямую
![]()
![]() до ее пересечения со следом
до ее пересечения со следом![]() .
Полученная точка пересечения – искомая
точка
.
Полученная точка пересечения – искомая
точка![]() .
.
Соединяем
последовательно точки
![]() ,
,![]() и
и![]() ,
и получаем натуральную величину
треугольникаABC.
,
и получаем натуральную величину
треугольникаABC.
Способ плоскопараллельного перемещения. Плоскопараллельное перемещение основано на способе вращения без указания осей вращения. Например, вращая отрезок прямой общего положения до положения, параллельного какой-либо плоскости проекций, можно заметить, что одна из его проекций не меняет своей длины при ее повороте параллельно оси проекций.
Пример 25. Определить натуральную величину отрезка АВ общего положения (рис. 54, а).
|
|
|
|
а) |
б) |
Рис. 54
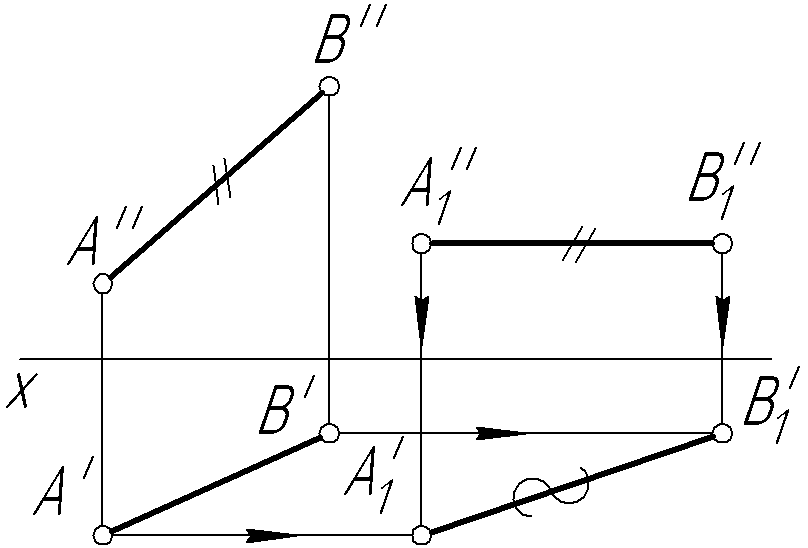
в)
Рис. 54. Продолжение
Решение.
Располагаем
горизонтальную проекцию А'В'
отрезка АВ
параллельно оси проекций x
(рис. 54,
б),
сохраняя ее длину (![]() ║x,
║x,
![]() = =А'В').
Фронтальные проекции точек А
и В
перемещаются по линиям, параллельным
оси проекций х.
На пересечении линий связи и этих прямых
получаем фронтальные проекции
= =А'В').
Фронтальные проекции точек А
и В
перемещаются по линиям, параллельным
оси проекций х.
На пересечении линий связи и этих прямых
получаем фронтальные проекции
![]() и
и
![]() точек
А
и В
соответственно после перемещения.
Соединяем точки А''
и
В''
и
получаем натуральную величину отрезка.
точек
А
и В
соответственно после перемещения.
Соединяем точки А''
и
В''
и
получаем натуральную величину отрезка.
Аналогично можно определить натуральную величину отрезка АВ, приведя его плоскоспараллельным перемещением в горизонтальное положение (рис. 54, в).
|
|
|
а) Рис. 55 |
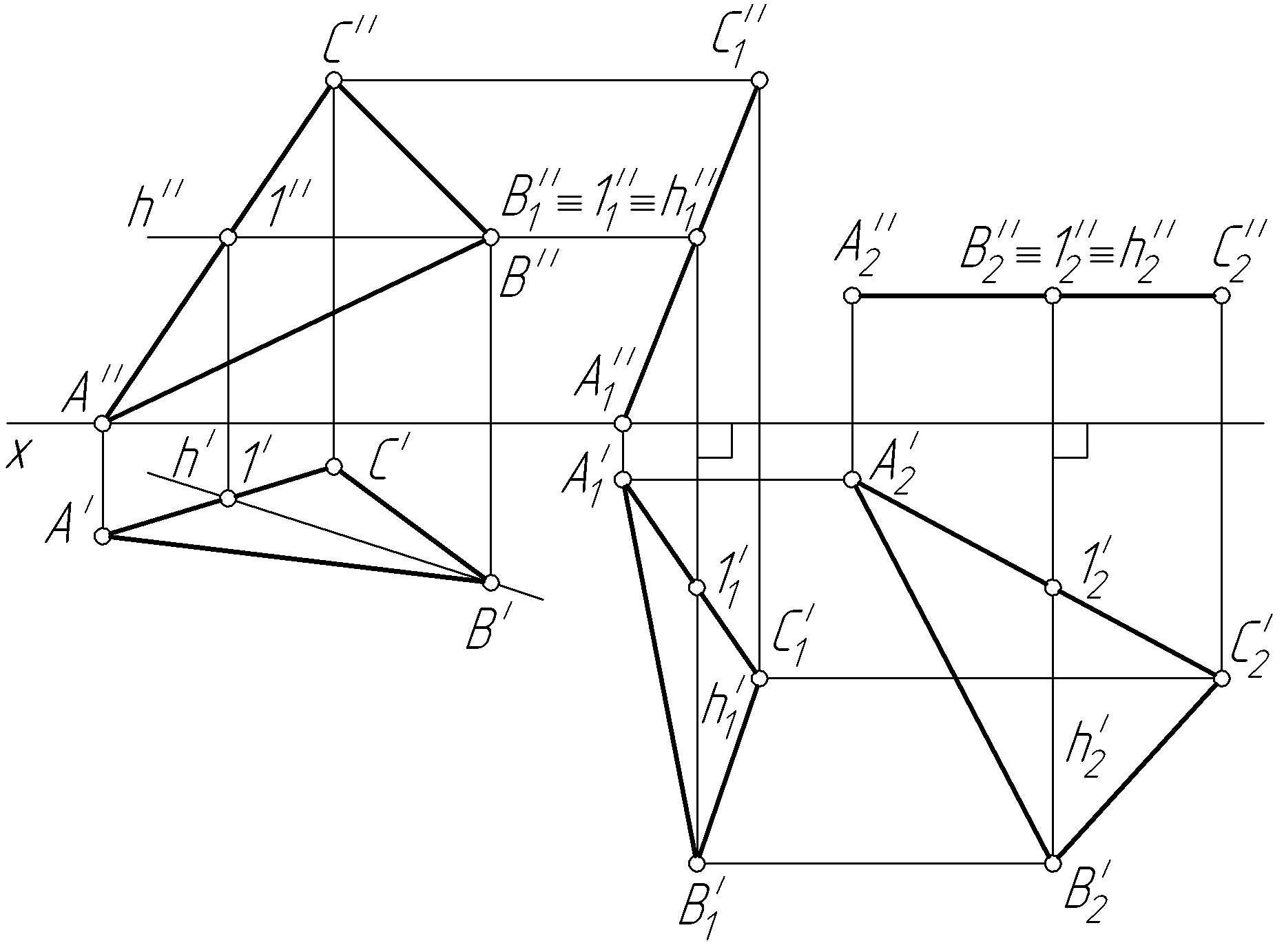
Решение. Преобразуем плоскость треугольника ABC перемещением из общего положения в положение, параллельное горизонтальной плоскости проекций (рис. 55, б).
Переместим
горизонтальную проекцию
![]() треугольникаABC
так, чтобы он занял фронтально-проецирующее
положение. Затем,
треугольникаABC
так, чтобы он занял фронтально-проецирующее
положение. Затем,
б)
Рис. 55. Продолжение
перемещая
плоскость треугольника в положение,
параллельное горизонтальной плоскости
проекций, определяем его натуральную
величину. Строим в треугольнике АВС
горизонталь h
(![]() ,
,![]() ).
Располагаем горизонтальную проекцию
).
Располагаем горизонтальную проекцию
![]() треугольника так, чтобы проекция
треугольника так, чтобы проекция
![]() была перпендикулярна оси проекцийx.
Для этого произвольно выбираем положение
точки
была перпендикулярна оси проекцийx.
Для этого произвольно выбираем положение
точки
![]() и через нее перпендикулярноx
строим прямую, на которой откладываем
отрезок равный отрезку горизонтали
и через нее перпендикулярноx
строим прямую, на которой откладываем
отрезок равный отрезку горизонтали
![]()
![]() .
Таким образом, определяется положение
новой горизонтальной проекции
.
Таким образом, определяется положение
новой горизонтальной проекции
![]() ,
сохраняющей форму и размеры
,
сохраняющей форму и размеры
![]() .
По известным отрезкам С'1',
А'1',
А'В',
В'С',
С'А'
строим горизонтальную проекцию
.
По известным отрезкам С'1',
А'1',
А'В',
В'С',
С'А'
строим горизонтальную проекцию
![]() .
Фронтальные проекции точек перемещаются
по линиям, параллельным осих.
Фронтальная проекция
.
Фронтальные проекции точек перемещаются
по линиям, параллельным осих.
Фронтальная проекция
![]() вырождается в прямую линию.Затем
перемещаем плоскость треугольника в
положение параллельное горизонтальной
плоскости проекций. При этом
вырождается в прямую линию.Затем
перемещаем плоскость треугольника в
положение параллельное горизонтальной
плоскости проекций. При этом
![]() параллельна осих,
и
параллельна осих,
и
![]() =
=
![]() ,
,![]() =
=![]() .
Горизонтальные проекции при втором
переносе перемещаются параллельно осих.
Построенная горизонтальная проекция
.
Горизонтальные проекции при втором
переносе перемещаются параллельно осих.
Построенная горизонтальная проекция
![]() является натуральной величиной.
является натуральной величиной.
Способ совмещения. Способ совмещения является частным случаем способа вращения. Его сущность состоит в том, что плоскость вращается вокруг одного из ее следов до совмещения с соответствующей плоскостью проекций. В совмещенном с плоскостью проекций положении любой плоский геометрический объект сохраняет свои истинные линейные и угловые размеры.
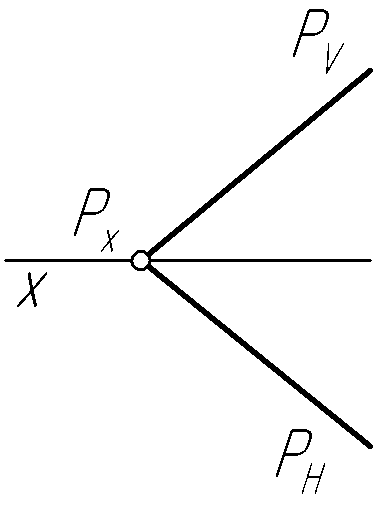
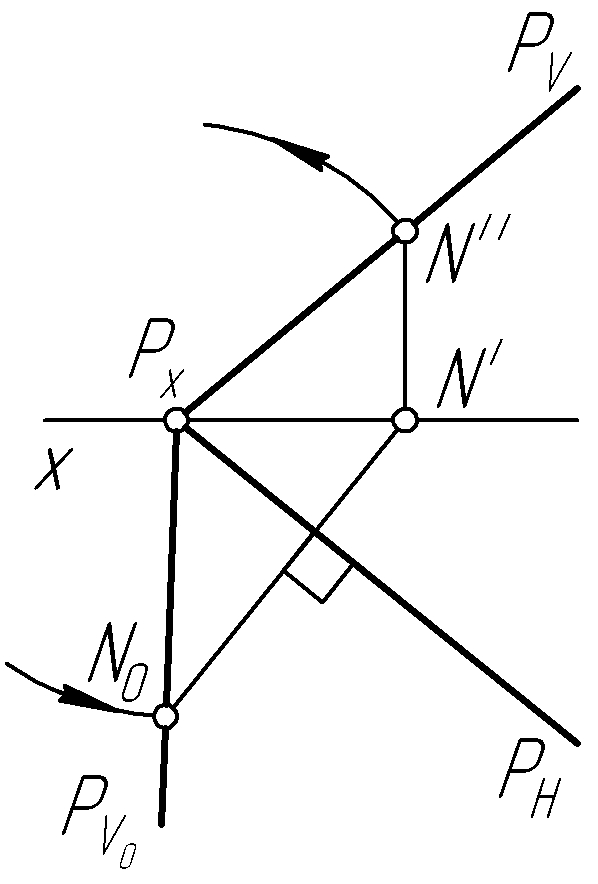
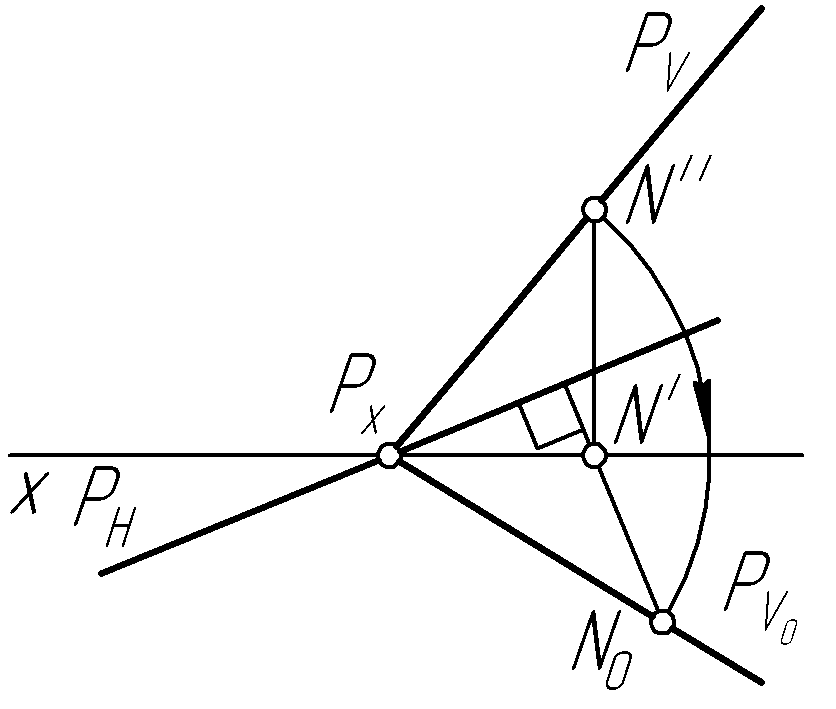
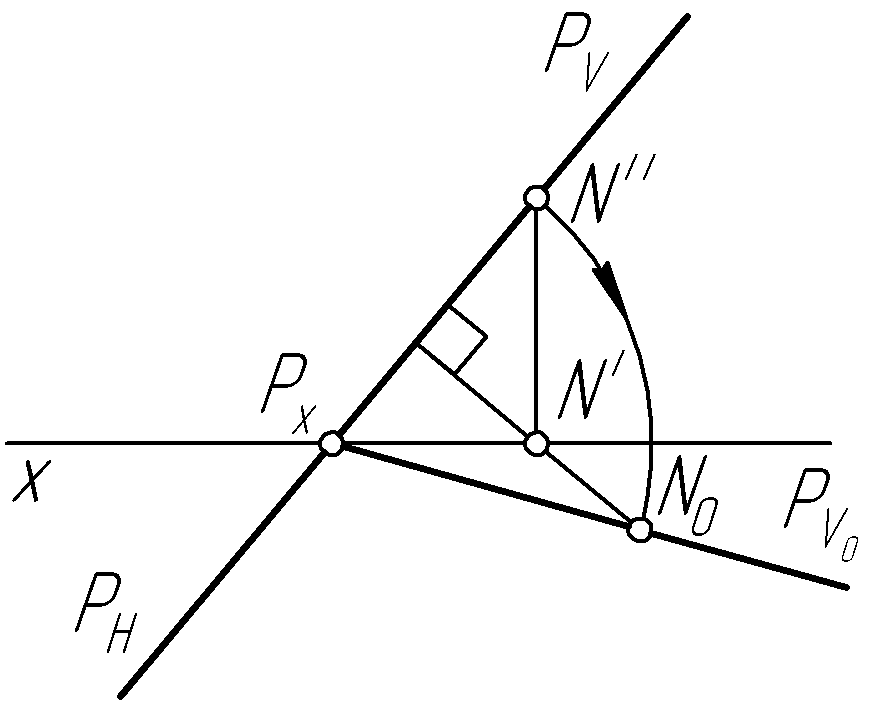
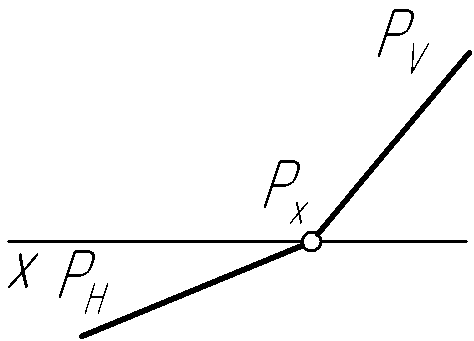
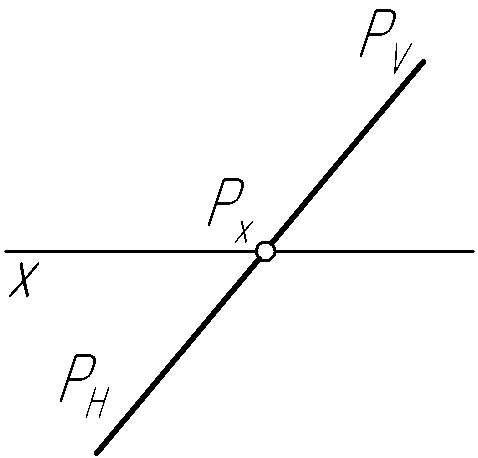
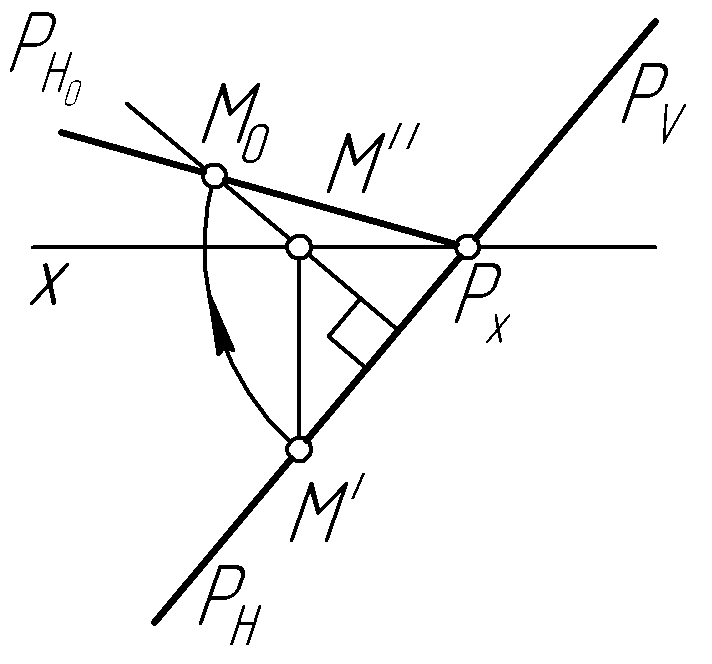
Пример 27. Построить совмещенный с горизонтальной плоскостью проекций фронтальный след плоскости Р общего положения (рис. 56, а, в, д).
Решение.
Для построения совмещенного фронтального
следа
![]() с горизонтальной плоскостью проекций
(рис. 56,б,
г,
е)
выбираем на следе
с горизонтальной плоскостью проекций
(рис. 56,б,
г,
е)
выбираем на следе
![]() произвольную точкуN
(N',
N'')
и
вращаем ее вокруг следа
произвольную точкуN
(N',
N'')
и
вращаем ее вокруг следа
![]() до совмещения с горизонтальной плоскостью
проекций. Проекция
до совмещения с горизонтальной плоскостью
проекций. Проекция![]() принадлежит следу
принадлежит следу![]() ,
а
,
а![]() – лежит на осиx.
Через точку
– лежит на осиx.
Через точку
![]() строим прямую (след горизонтально-проецирующей
плоскости, в которой вращается точкаN),
перпендикулярную следу
строим прямую (след горизонтально-проецирующей
плоскости, в которой вращается точкаN),
перпендикулярную следу
![]() (или его продолжению). Раствором циркуля,
равным
(или его продолжению). Раствором циркуля,
равным![]() ,
проводим дугу с центром в точке
,
проводим дугу с центром в точке![]() до пересечения ее с построенным ранее
перпендикуляром. На пересечении этих
линий получаем совмещенное положение
до пересечения ее с построенным ранее
перпендикуляром. На пересечении этих
линий получаем совмещенное положение![]() точкиN
с горизонтальной плоскостью проекций.
Через неподвижную точку
точкиN
с горизонтальной плоскостью проекций.
Через неподвижную точку
![]() схода следов, которая принадлежит оси
вращения, и совмещенное положение
схода следов, которая принадлежит оси
вращения, и совмещенное положение![]() проводим совмещенный фронтальный след
проводим совмещенный фронтальный след![]() плоскостиР.
плоскостиР.
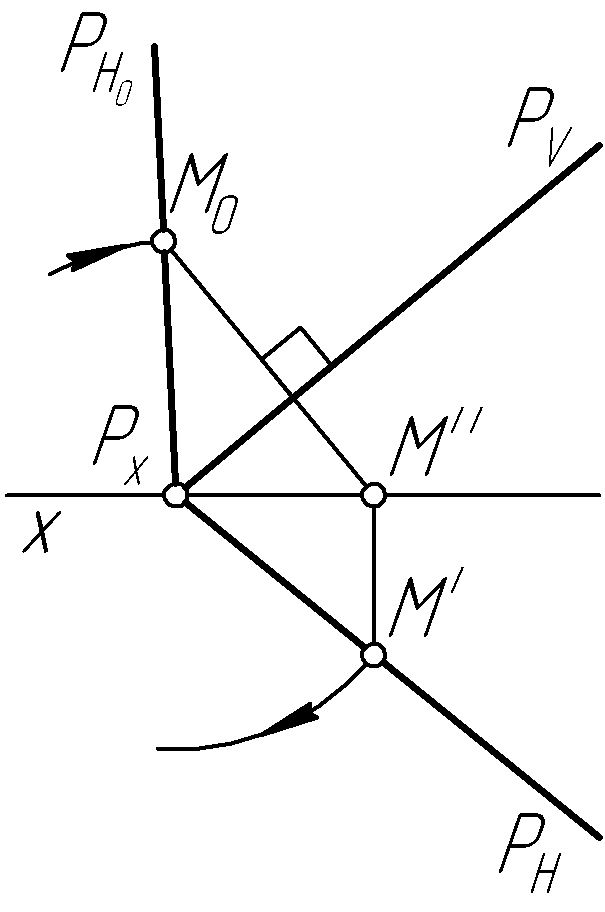
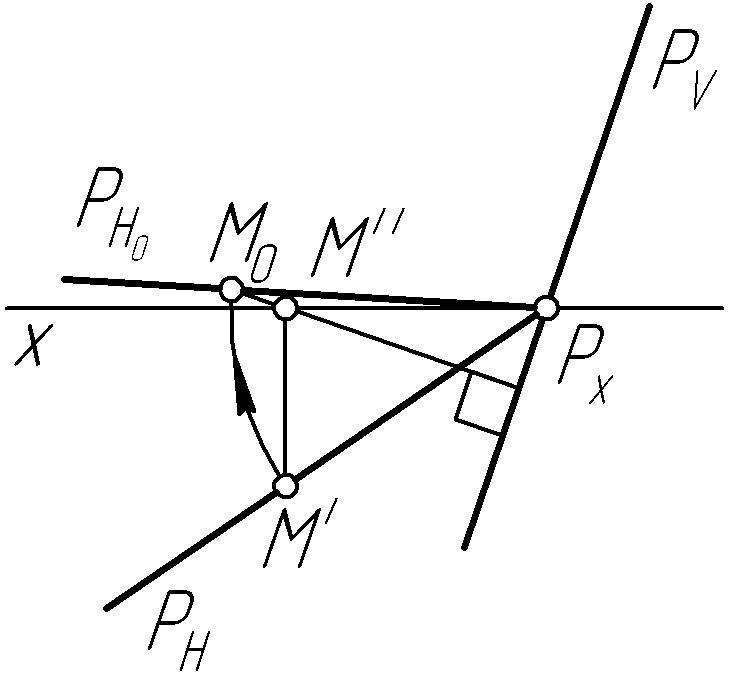
Пример 28. Построить совмещенный с фронтальной плоскостью проекций горизонтальный след плоскости Р общего положения (рис. 57, а, в, д).
Решение.
Для построения совмещенного горизонтального
следа
![]() с фронтальной плоскостью проекций (рис.
57,б,
г,
е)
выбираем на следе
с фронтальной плоскостью проекций (рис.
57,б,
г,
е)
выбираем на следе
![]() произвольную точкуM
(M',
M'')
и вращаем ее
вокруг следа
произвольную точкуM
(M',
M'')
и вращаем ее
вокруг следа
![]() до совмещения с фронтальной плоскостью
проекций. ПроекцияM'
принадлежит следу
до совмещения с фронтальной плоскостью
проекций. ПроекцияM'
принадлежит следу
![]() плоскости, а
плоскости, а
![]() –
лежит на осиx.
Через точку
–
лежит на осиx.
Через точку
![]() строим прямую(след
фронтально-проецирующей плоскости, в
которой вращается точка М),
перпендикулярную следу
строим прямую(след
фронтально-проецирующей плоскости, в
которой вращается точка М),
перпендикулярную следу
![]() .
Раствором циркуля, равным
.
Раствором циркуля, равным![]() ,
проводим дугу с центром в точке
,
проводим дугу с центром в точке![]() до пересечения ее с построенным ранее
перпендикуляром. На пересечении этих
линий получаем совмещенное положение
до пересечения ее с построенным ранее
перпендикуляром. На пересечении этих
линий получаем совмещенное положение![]() точкиМ
с фронтальной плоскостью проекций.
Через неподвижную точку
точкиМ
с фронтальной плоскостью проекций.
Через неподвижную точку
![]() схода следов, которая принадлежит оси
вращения, и совмещенное положение
схода следов, которая принадлежит оси
вращения, и совмещенное положение![]() проводим совмещенный след
проводим совмещенный след![]() плоскостиР.
плоскостиР.
|
|
|
|
а) |
б) |
|
|
|
|
в) |
г) |
|
|
|
|
д) |
е) |
Рис. 56
|
|
|
|
а) |
б) |
|
|
|
|
в) |
г) |
|
|
|
|
д) |
е) |
Рис. 57
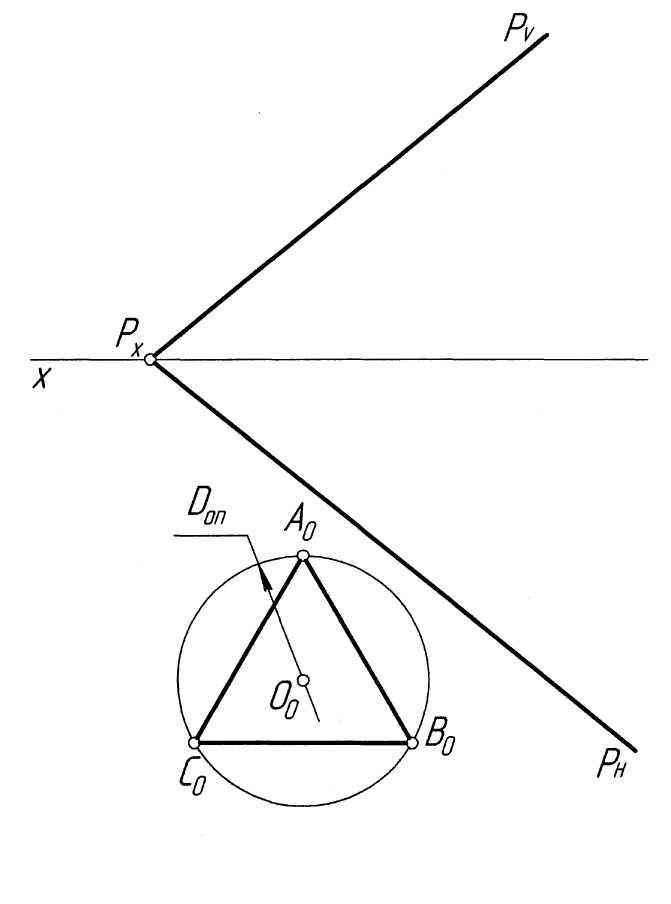
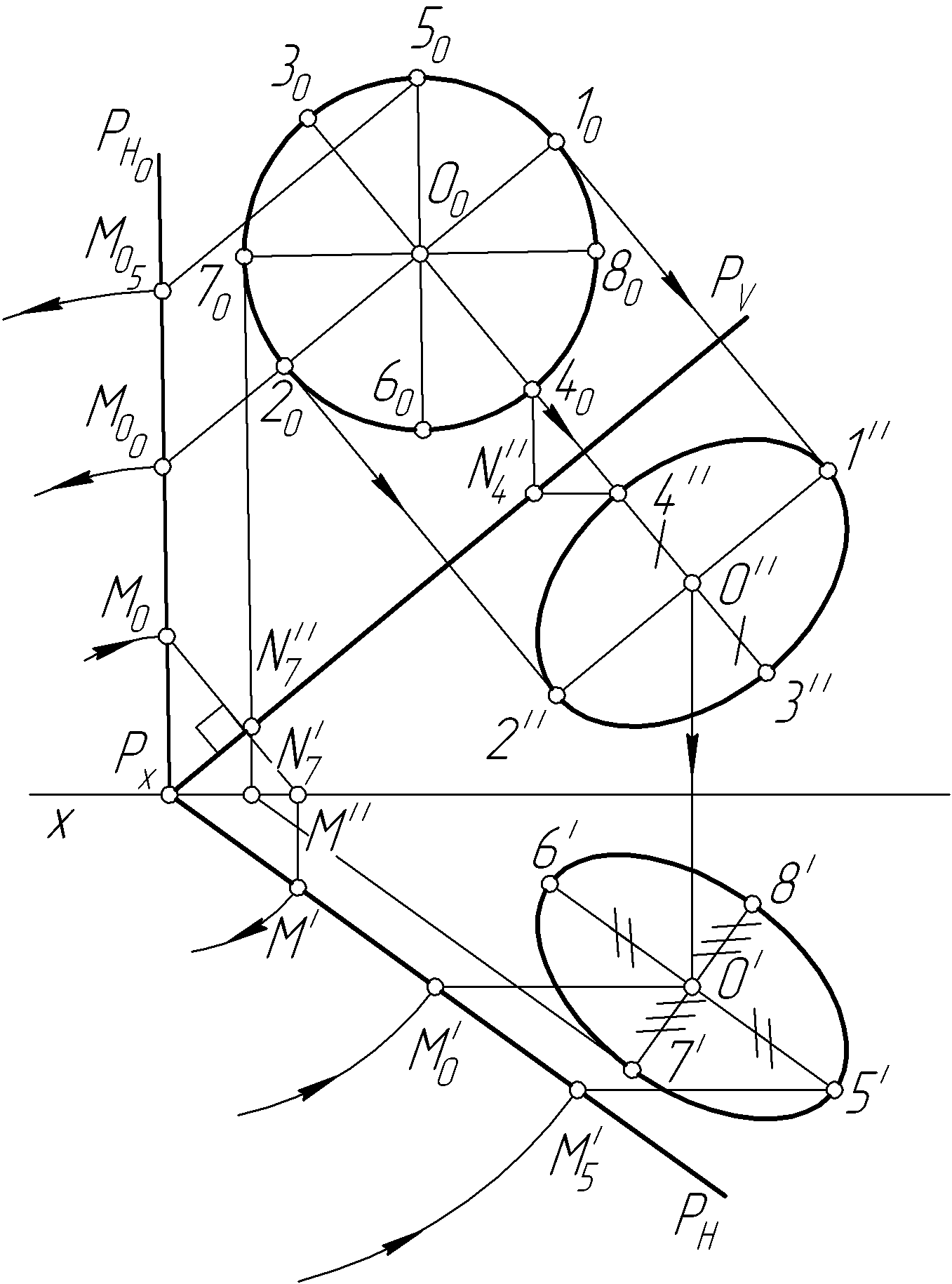
Пример 29. Построить проекции правильного треугольника ABC, принадлежащего плоскости P общего положения, если задано совмещенное с горизонтальной плоскостью проекций положение центра О0 описанной вокруг него окружности диаметром Dоп (рис. 58, а).
Решение. Поскольку центр О (О0) описанной окружности задан в совмещенном с горизонтальной плоскостью проекций положении, необходимо
|
|
|
|
а) |
б) |
Рис. 58
вначале выполнить
построение совмещенного фронтального
следа
![]() заданной плоскостиP
(рис. 58, б).
Построение совмещенного фронтального
следа с горизонтальной плоскостью
проекций подробно рассмотрено в
примере 27. Затем строим окружность
заданного диаметра Dоп
и в ней правильный треугольник
заданной плоскостиP
(рис. 58, б).
Построение совмещенного фронтального
следа с горизонтальной плоскостью
проекций подробно рассмотрено в
примере 27. Затем строим окружность
заданного диаметра Dоп
и в ней правильный треугольник
![]() (положение его вершин выбрано произвольно).
(положение его вершин выбрано произвольно).
Через вершины
![]() ,
,![]() и
и![]() треугольника проводим совмещенные
горизонтали
треугольника проводим совмещенные
горизонтали![]() ,
,![]() ,
,![]() параллельно следу
параллельно следу![]() ,
определяем точки
,
определяем точки![]() ,
,![]() ,
,![]() их пересечения с совмещенным фронтальным
следом
их пересечения с совмещенным фронтальным
следом![]() (совмещенные фронтальные следы этих
горизонталей), и обратным вращением
поднимаем плоскостьP
в первоначальное положение. Отмечаем
на следе
(совмещенные фронтальные следы этих
горизонталей), и обратным вращением
поднимаем плоскостьP
в первоначальное положение. Отмечаем
на следе
![]() фронтальные следы
фронтальные следы![]() (
(![]() ),
),![]() (
(![]() ),
),![]() (
(![]() )
горизонталей, и через эти следы строим
проекции горизонталей
)
горизонталей, и через эти следы строим
проекции горизонталей![]() ,
,![]() ,
,![]() плоскости. При обратном вращении
плоскостиP
проекции
плоскости. При обратном вращении
плоскостиP
проекции
![]() ,
,![]() ,
,![]() перемещаются по прямым, перпендикулярным
оси вращения – горизонтальному следу
перемещаются по прямым, перпендикулярным
оси вращения – горизонтальному следу![]() плоскости (
плоскости (![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ).
При пересечении этих прямых с
соответствующими горизонтальными
проекциями горизонталей плоскостиР
получаем горизонтальные проекции
).
При пересечении этих прямых с
соответствующими горизонтальными
проекциями горизонталей плоскостиР
получаем горизонтальные проекции
![]() ,
,![]() ,
,![]() точекА,
В
и С
соответственно. Проецируем эти точки
на фронтальные проекции горизонталей
и получаем фронтальные проекции
точекА,
В
и С
соответственно. Проецируем эти точки
на фронтальные проекции горизонталей
и получаем фронтальные проекции
![]() ,
,![]() и
и![]() вершинА,
В
и С треугольника.
Соединив одноименные проекции точек
А
(
вершинА,
В
и С треугольника.
Соединив одноименные проекции точек
А
(![]() ,
,![]() ),В
(
),В
(![]() ,
,![]() )
иС
(
)
иС
(![]() ,
,![]() ),
получаем проекции искомого треугольникаABC,
принадлежащего плоскости P.
),
получаем проекции искомого треугольникаABC,
принадлежащего плоскости P.
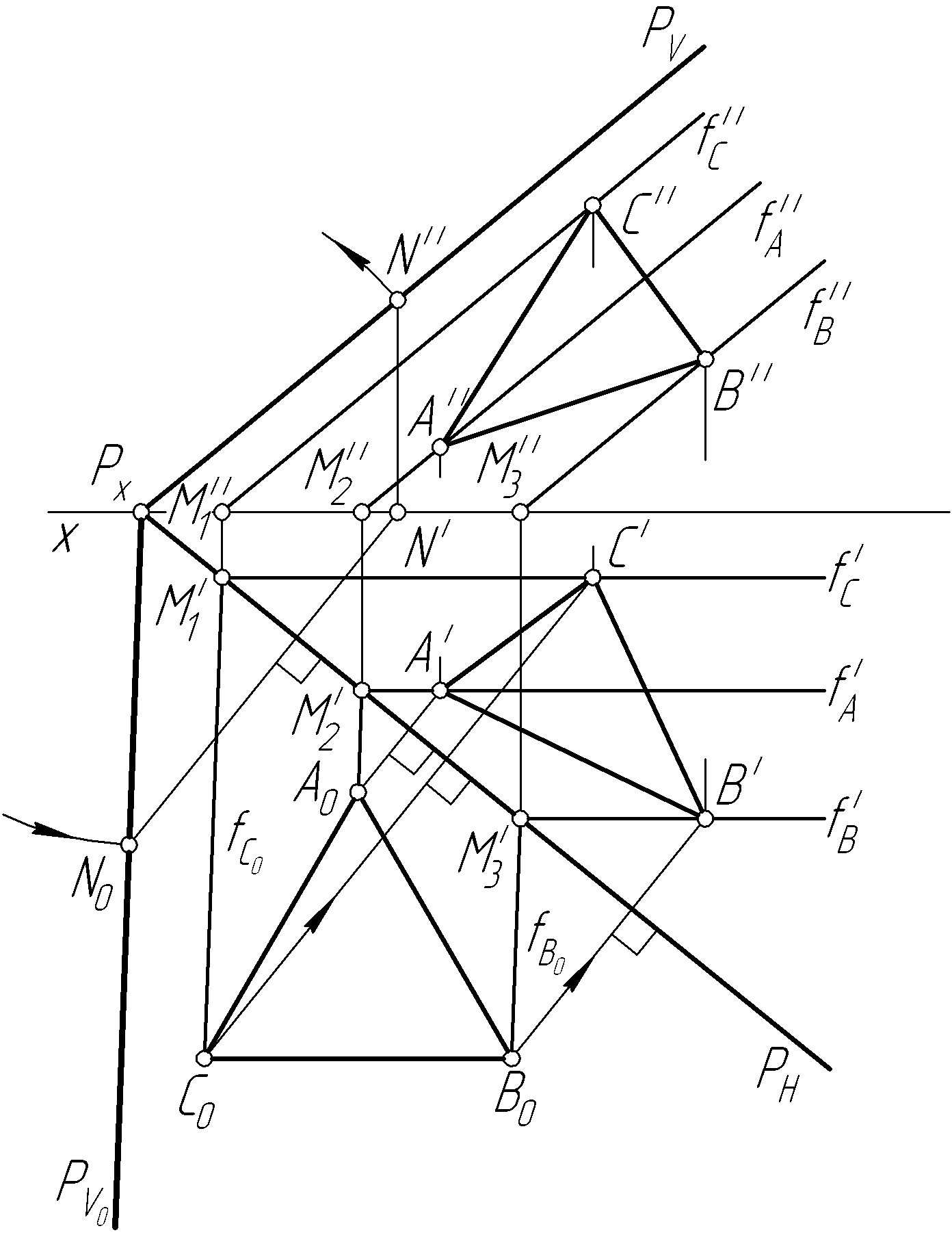
На рис. 59 для решения
этой задачи использованы фронтали
плоскости P.
Вначале строим совмещенный фронтальный
след
![]() .
Затем через вершины
.
Затем через вершины![]() ,
,![]() и
и![]() треугольника проводим совмещенные
фронтали параллельно совмещенному
фронтальному следу
треугольника проводим совмещенные
фронтали параллельно совмещенному
фронтальному следу![]() .
На их пересечении со следом
.
На их пересечении со следом![]() получаем проекции
получаем проекции![]() ,
,![]() ,
,![]() горизонтальных следов
горизонтальных следов![]() ,
,![]() ,
,![]() фронталей и проводим через них проекции
фронталей плоскости. При обратном
вращении плоскостиP
горизонтальные проекции
фронталей и проводим через них проекции
фронталей плоскости. При обратном
вращении плоскостиP
горизонтальные проекции
![]() ,
,![]() ,
,![]() точекA,
B
и C
перемещаются по прямым, перпендикулярным
оси вращения – следу
точекA,
B
и C
перемещаются по прямым, перпендикулярным
оси вращения – следу
![]() плоскости. При пересечении этих прямых
с соответствующими горизонтальными
проекциями фронталей плоскостиР
получаем проекции
плоскости. При пересечении этих прямых
с соответствующими горизонтальными
проекциями фронталей плоскостиР
получаем проекции
![]() ,
,![]() ,
,![]() .
Проецируем эти точки на фронтальные
проекции фронталей и получаем проекции
.
Проецируем эти точки на фронтальные
проекции фронталей и получаем проекции![]() ,
,![]() и
и![]() соответствующих вершин
треугольника.
Соединив одноименные проекции точек
А (
соответствующих вершин
треугольника.
Соединив одноименные проекции точек
А (![]() ,
,![]() ),В
(
),В
(![]() ,
,![]() )
иС
(
)
иС
(![]() ,
,![]() ),
получаем проекции искомого треугольникаABC,
принадлежащего плоскости P.
),
получаем проекции искомого треугольникаABC,
принадлежащего плоскости P.
Рис. 59
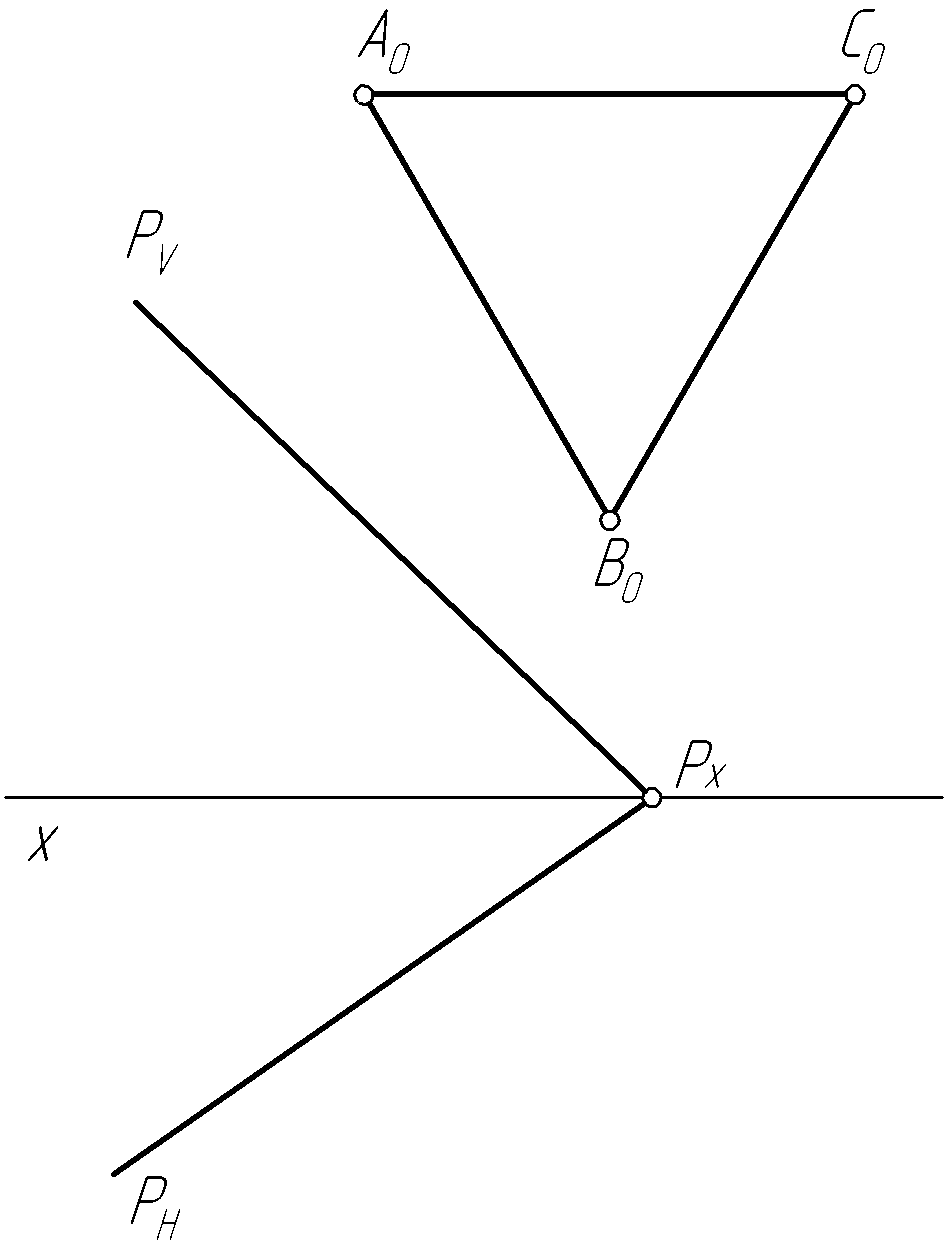
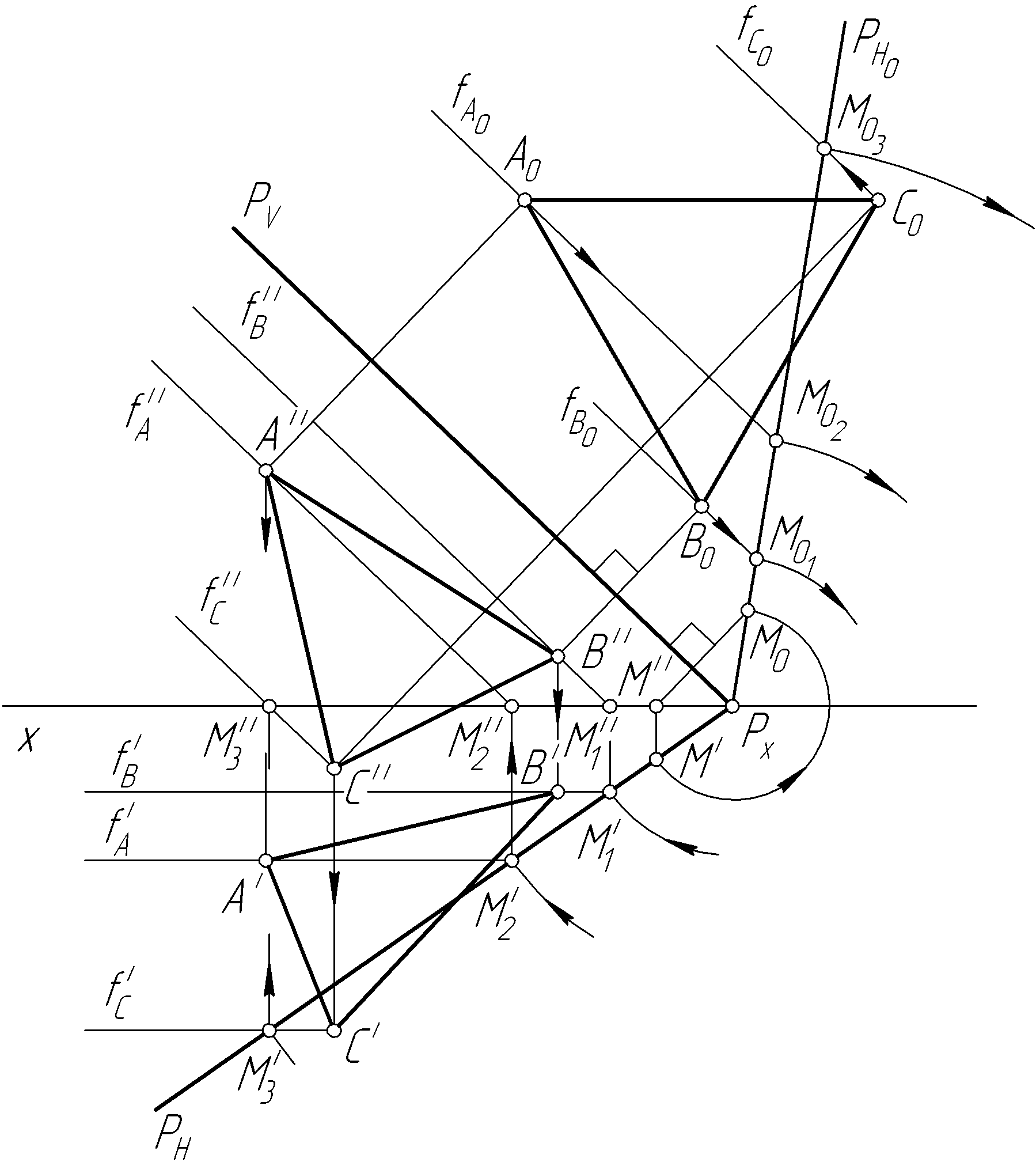
Пример 30. Построить проекции треугольника ABC, принадлежащего плоскости P общего положения, если задано его совмещенное положение с фронтальной плоскостью проекций (рис. 60, а).
Решение.
Поскольку треугольник задан в положении,
совмещенном с фронтальной плоскостью
проекций, необходимо вначале выполнить
построение совмещенного горизонтального
следа
![]() заданной плоскостиP
(рис. 60, б).
Построение совмещенного горизонтального
следа с фронтальной плоскостью проекций
подробно рассмотрено в примере 28. Через
вершины
заданной плоскостиP
(рис. 60, б).
Построение совмещенного горизонтального
следа с фронтальной плоскостью проекций
подробно рассмотрено в примере 28. Через
вершины
![]() ,
,![]() и
и![]() треугольника проводим совмещенные
фронтали параллельно следу
треугольника проводим совмещенные
фронтали параллельно следу![]() ,
определяем точки
,
определяем точки![]() ,
,![]() и
и![]() их пересечения с совмещенным горизонтальным
следом
их пересечения с совмещенным горизонтальным
следом![]() (совмещенные горизонтальные следы
этих фронталей) и обратным вращением
возвращаем плоскостьP
в
(совмещенные горизонтальные следы
этих фронталей) и обратным вращением
возвращаем плоскостьP
в
а)
б)
Рис. 60
первоначальное
положение. Отмечаем на следе
![]() горизонтальные следы
горизонтальные следы![]() (
(![]() ),
),![]() (
(![]() ),
),![]() (
(![]() )
фронталей и через эти следы строим
проекции фронталей
)
фронталей и через эти следы строим
проекции фронталей![]() ,
,![]() и
и![]() плоскости. При обратном вращении
плоскостиP
проекции
плоскости. При обратном вращении
плоскостиP
проекции
![]() ,
,![]() ,
,![]() перемещаются по прямым, перпендикулярным
оси вращения – следу
перемещаются по прямым, перпендикулярным
оси вращения – следу![]() плоскости (
плоскости (![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ).
При пересечении этих прямых с
соответствующими фронталями плоскостиР
получаем проекции
).
При пересечении этих прямых с
соответствующими фронталями плоскостиР
получаем проекции
![]() ,
,![]() ,
,![]() .
Проецируем эти точки на горизонтальные
проекции фронталей и получаем проекции
.
Проецируем эти точки на горизонтальные
проекции фронталей и получаем проекции![]() ,
,![]() и
и![]() соответствующих вершин треугольника.
Соединив одноименные проекции точекА
(
соответствующих вершин треугольника.
Соединив одноименные проекции точекА
(![]() ,
,![]() ),В
(
),В
(![]() ,
,![]() )
иС
(
)
иС
(![]() ,
,![]() ),
получаем проекции искомого треугольникаABC,
принадлежащего плоскости P.
),
получаем проекции искомого треугольникаABC,
принадлежащего плоскости P.
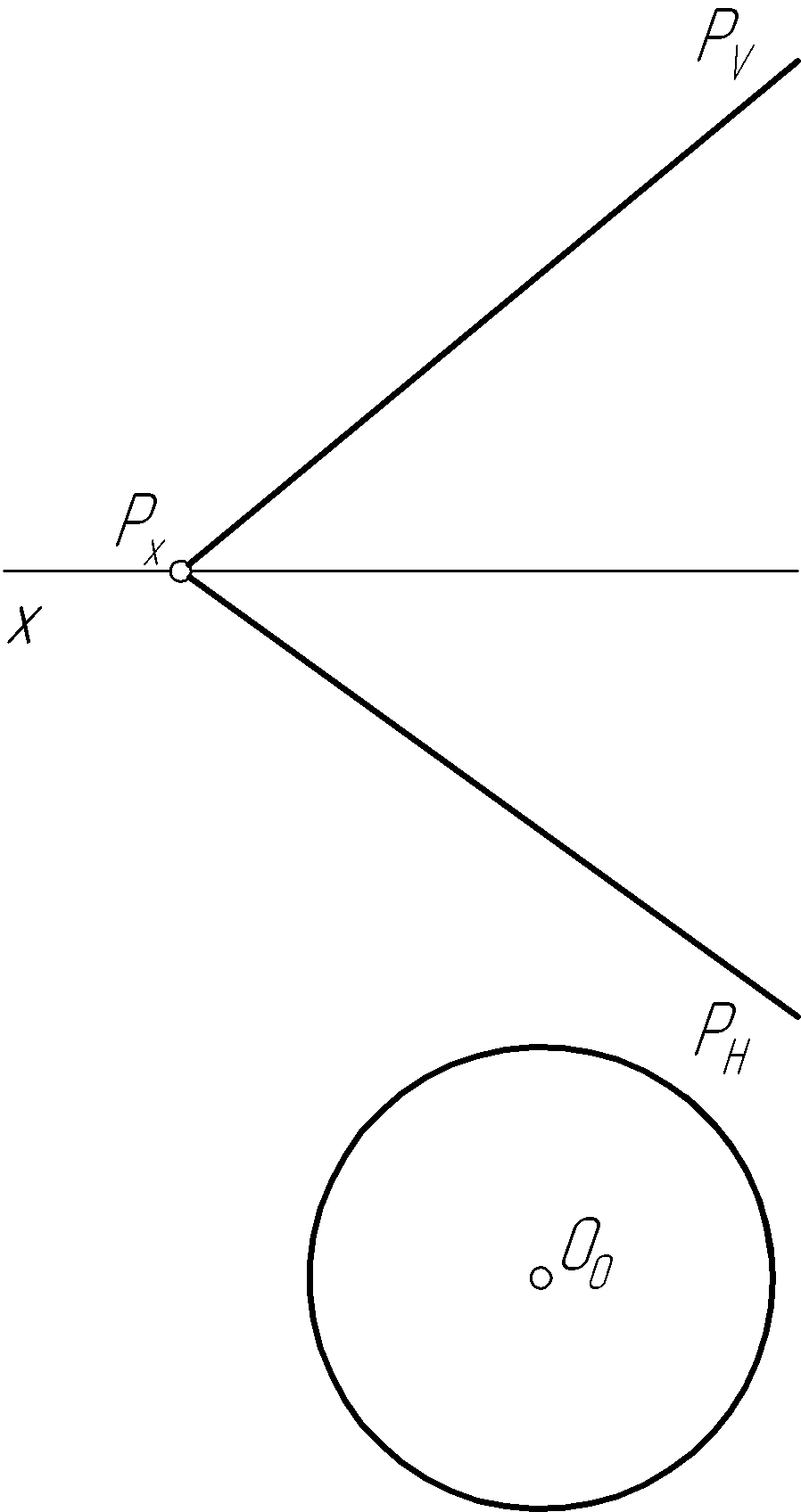
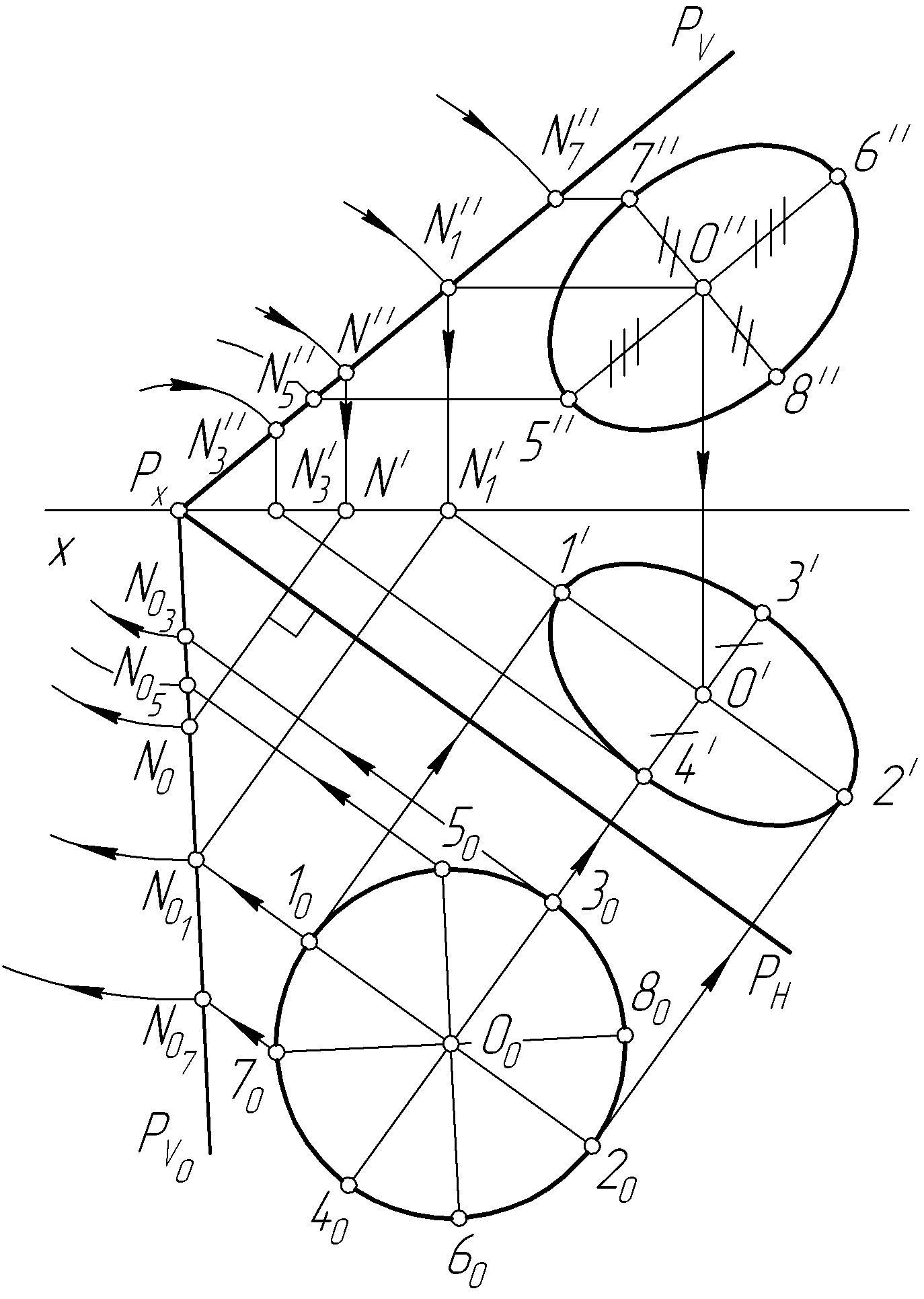
Пример 31. Построить проекции окружности, принадлежащей плоскости Р общего положения, если задано ее совмещенное положение с плоскостью проекций (рис. 61, а, в).
Решение.
Окружность,
принадлежащая плоскости общего положения,
на горизонтальную и фронтальную плоскости
проекций спроецируется в виде эллипсов
(рис. 61, б,
г). Причем
большая ось эллипса в горизонтальной
плоскости проекций параллельна
горизонтальному следу
![]() плоскостиР,
а большая ось эллипса во фронтальной
плоскости проекций параллельна
фронтальному следу
плоскостиР,
а большая ось эллипса во фронтальной
плоскости проекций параллельна
фронтальному следу
![]() плоскости. Малые оси эллипсов
перпендикулярны соответствующим большим
осям.
плоскости. Малые оси эллипсов
перпендикулярны соответствующим большим
осям.
Рассмотрим вначале
построение проекций окружности,
совмещенной с горизонтальной плоскостью
проекций (рис. 61, б).
Вначале в совмещенном положении
окружности строим диаметры, позволяющие
найти большие и малые оси эллипсов:
1020║![]() ,3040
,3040
![]()
![]() ,5060║
,5060║![]() и7080
и7080![]()
![]() .
Затем через точки
.
Затем через точки![]() и10
– 80
проводим
совмещенные горизонтали, определяем
их проекции в плоскости P
и строим на них соответствующие проекции
точек 1 (
и10
– 80
проводим
совмещенные горизонтали, определяем
их проекции в плоскости P
и строим на них соответствующие проекции
точек 1 (![]() ,
,![]() )
–8 (
)
–8 (![]() ,
,![]() ).
Соединяем плавной линией одноименные
проекции точек1 (
).
Соединяем плавной линией одноименные
проекции точек1 (![]() ,
,![]() )
–8 (
)
–8 (![]() ,
,![]() )
и получаем проекции окружности,
принадлежащей плоскостиP.
)
и получаем проекции окружности,
принадлежащей плоскостиP.
Построение проекций окружности, совмещенной с фронтальной плоскостью проекций, показано на рис. 61, г.
|
|
|
|
а) |
б) |
|
|
|
|
в) |
г) |
|
Рис. 61 | |
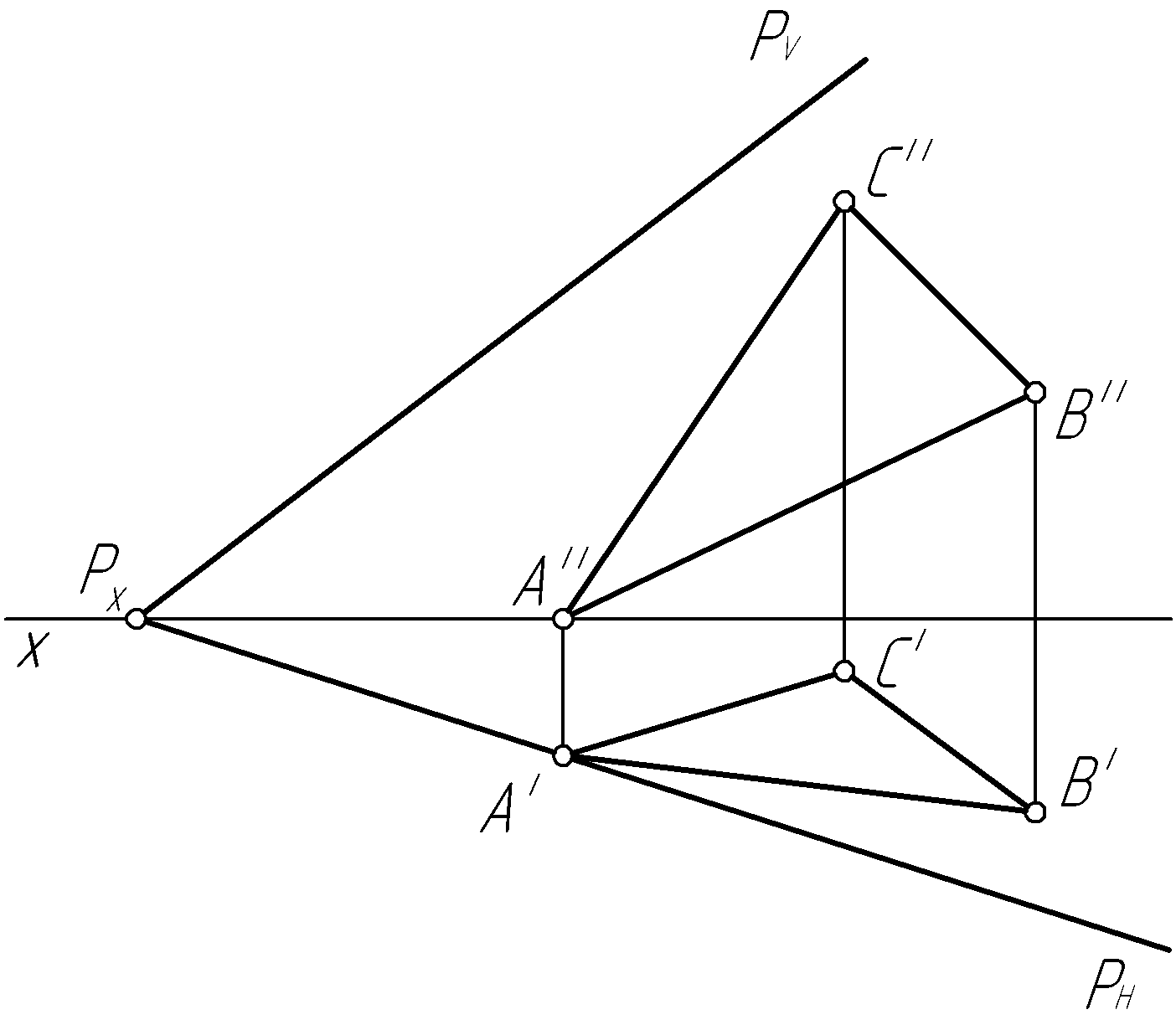
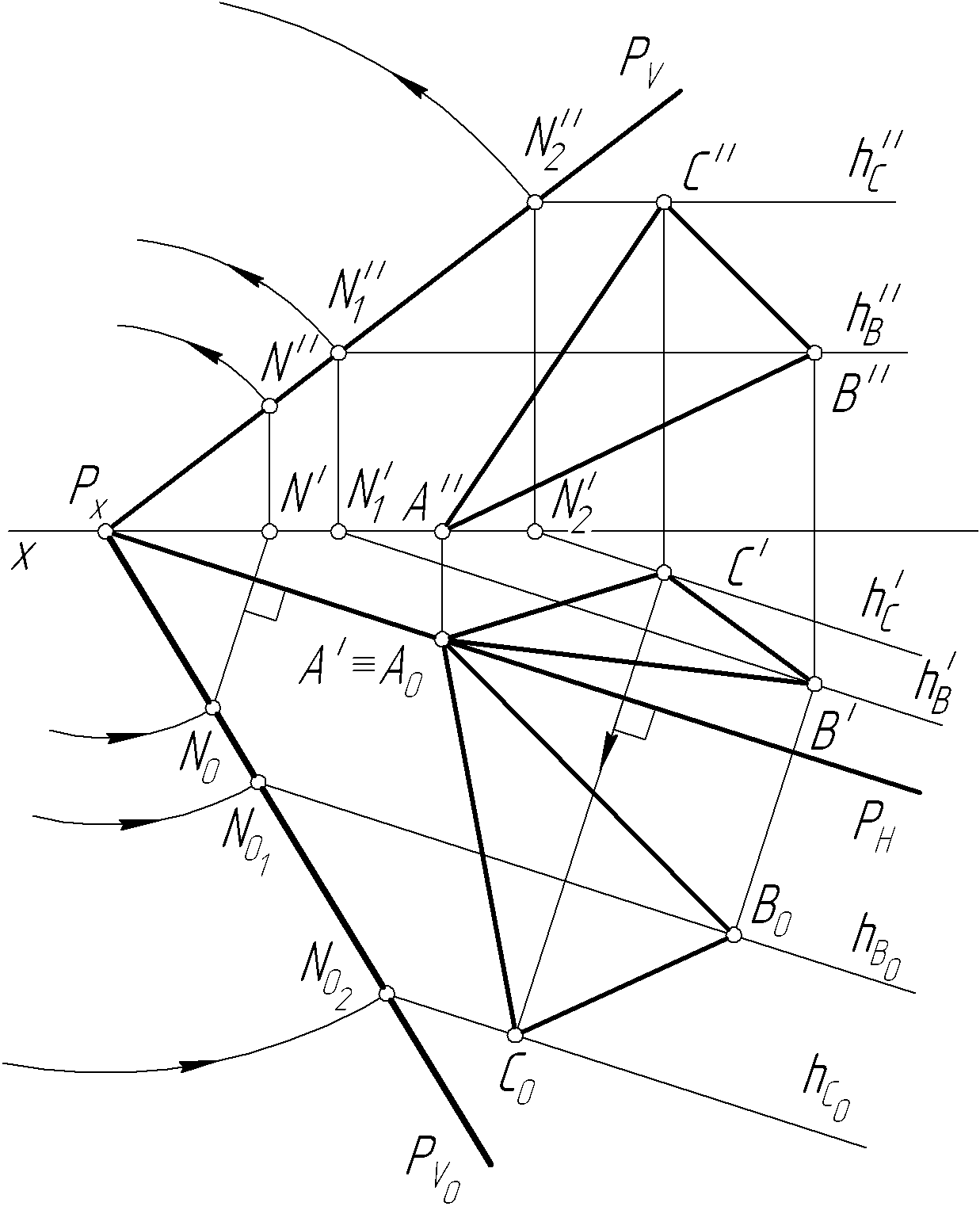
Пример 32. Определить натуральную величину треугольника ABC, принадлежащего плоскости Р общего положения, заданной следами (рис. 62, а).
а)
б)
Рис. 62
Решение.
Для
решения
задачи (рис. 62, б)
воспользуемся способом совмещения.
Проведем
через вершины треугольника горизонтали
![]() (
(![]() ,
,![]() )
и
)
и![]() (
(![]() ,
,![]() )
и совместим плоскостьР
с горизонтальной плоскостью проекций
(см. примеры 27 и 28). Используя фронтальные
следы
)
и совместим плоскостьР
с горизонтальной плоскостью проекций
(см. примеры 27 и 28). Используя фронтальные
следы
![]() и
и![]() горизонталей, строим совмещенное
положение
горизонталей, строим совмещенное
положение![]() заданного треугольника с горизонтальной
плоскостью проекций, которое и определяет
его натуральную величину.
заданного треугольника с горизонтальной
плоскостью проекций, которое и определяет
его натуральную величину.
Способ перемены плоскостей проекций (способ введения дополнительных плоскостей проекций). Этот способ преобразования проекций предполагает, что объекты проецирования сохраняют свое положение относительно плоскостей проекций неизменным. При этом вводятся новые плоскости проекций таким образом, чтобы геометрические объекты оказались в частном относительно них положении. При решении задач этим способом необходимо помнить следующее:
1) плоскости проекций всегда должны быть взаимно перпендикулярными;
2) линии, соединяющие проекции точек (линии связи), должны быть всегда перпендикулярны осям проекций;
3) расстояние от точки до плоскости проекций, не изменяющей своего положения в пространстве, остается постоянным.
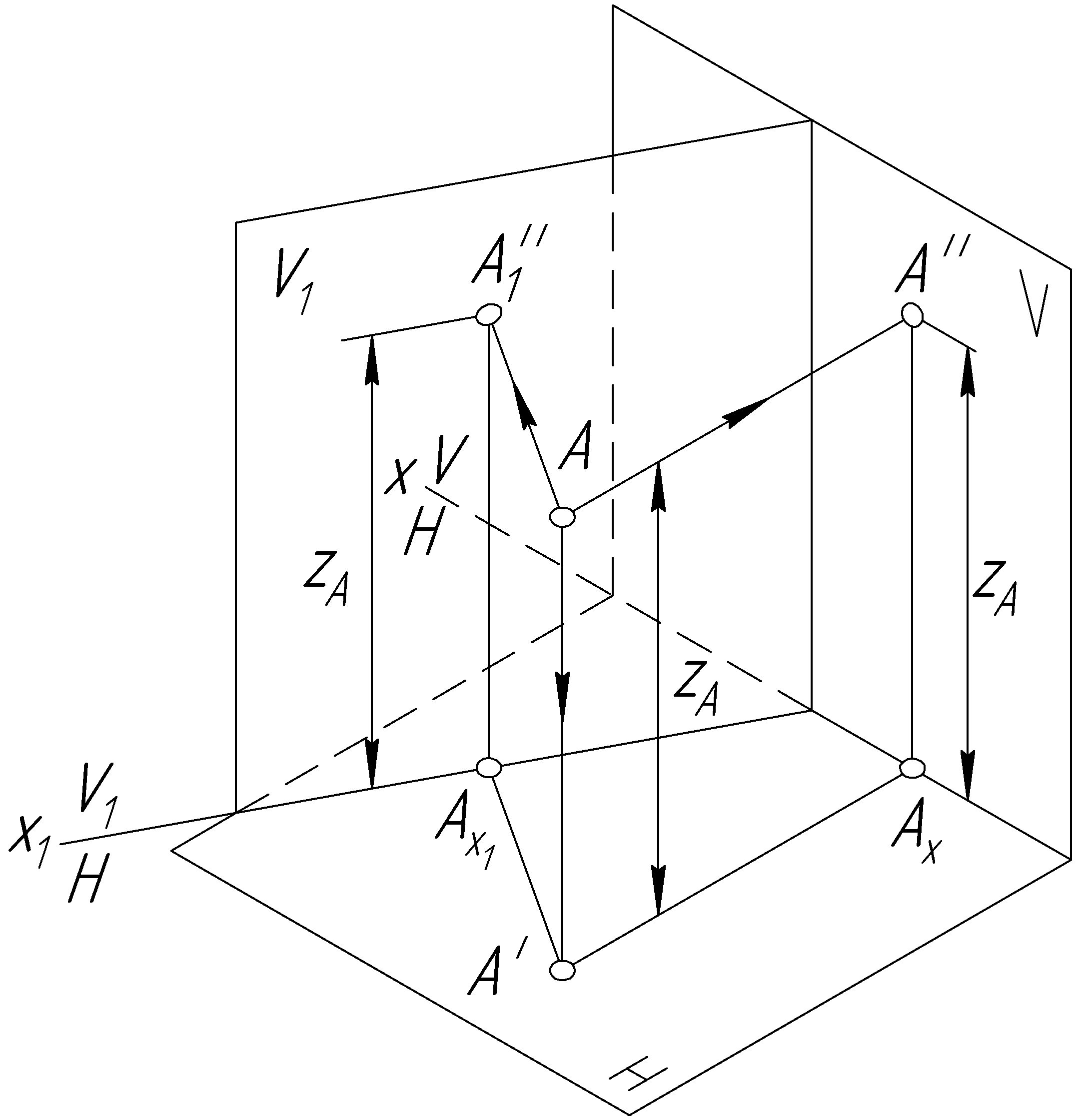
На рис. 63 показан принцип замены плоскостей проекций. Новая фронтальная плоскость V1 расположена перпендикулярно плоскости проекций Н. Линия пересечения х1 плоскостей проекций V1 и Н называется новой осью проекций.
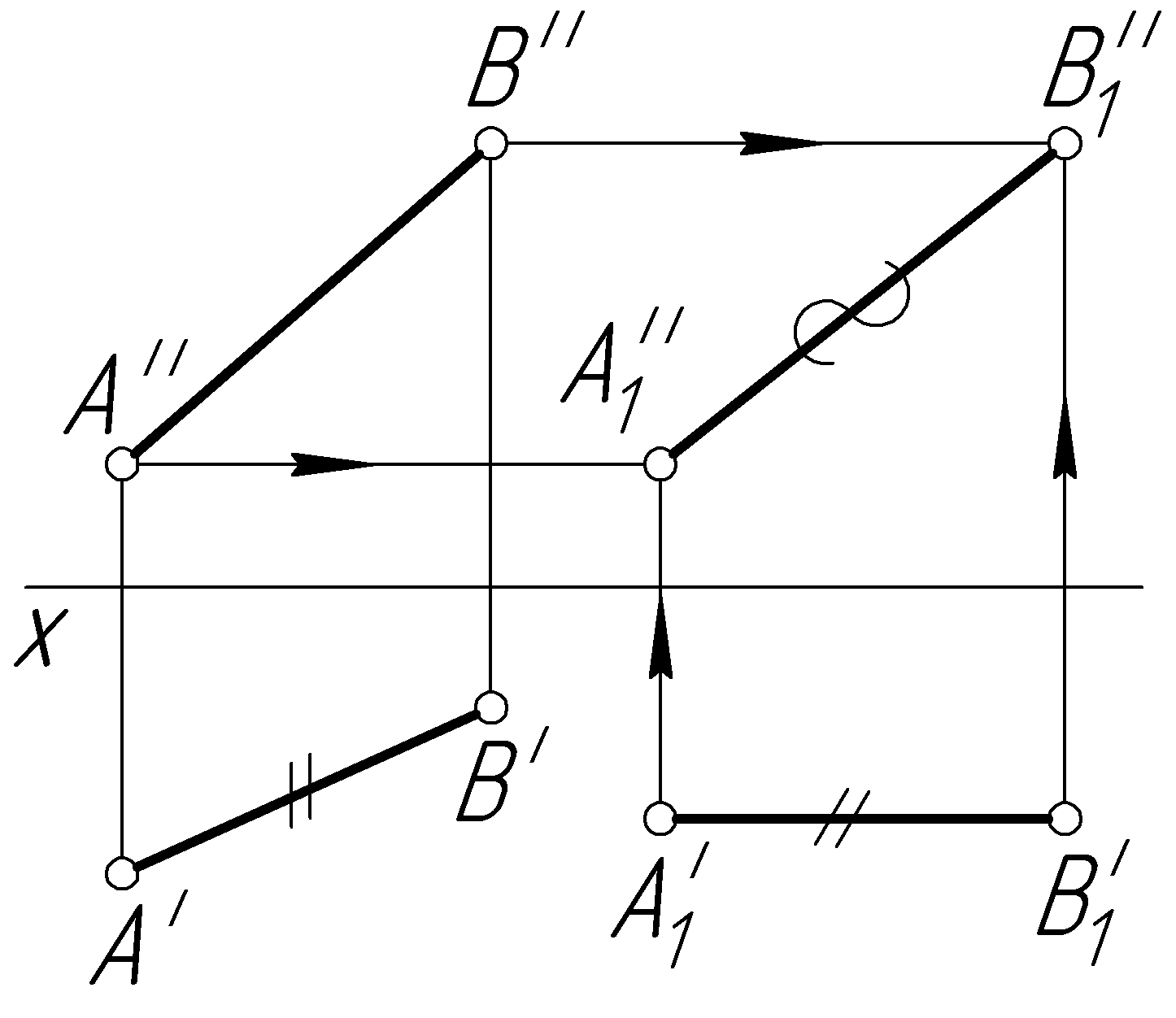
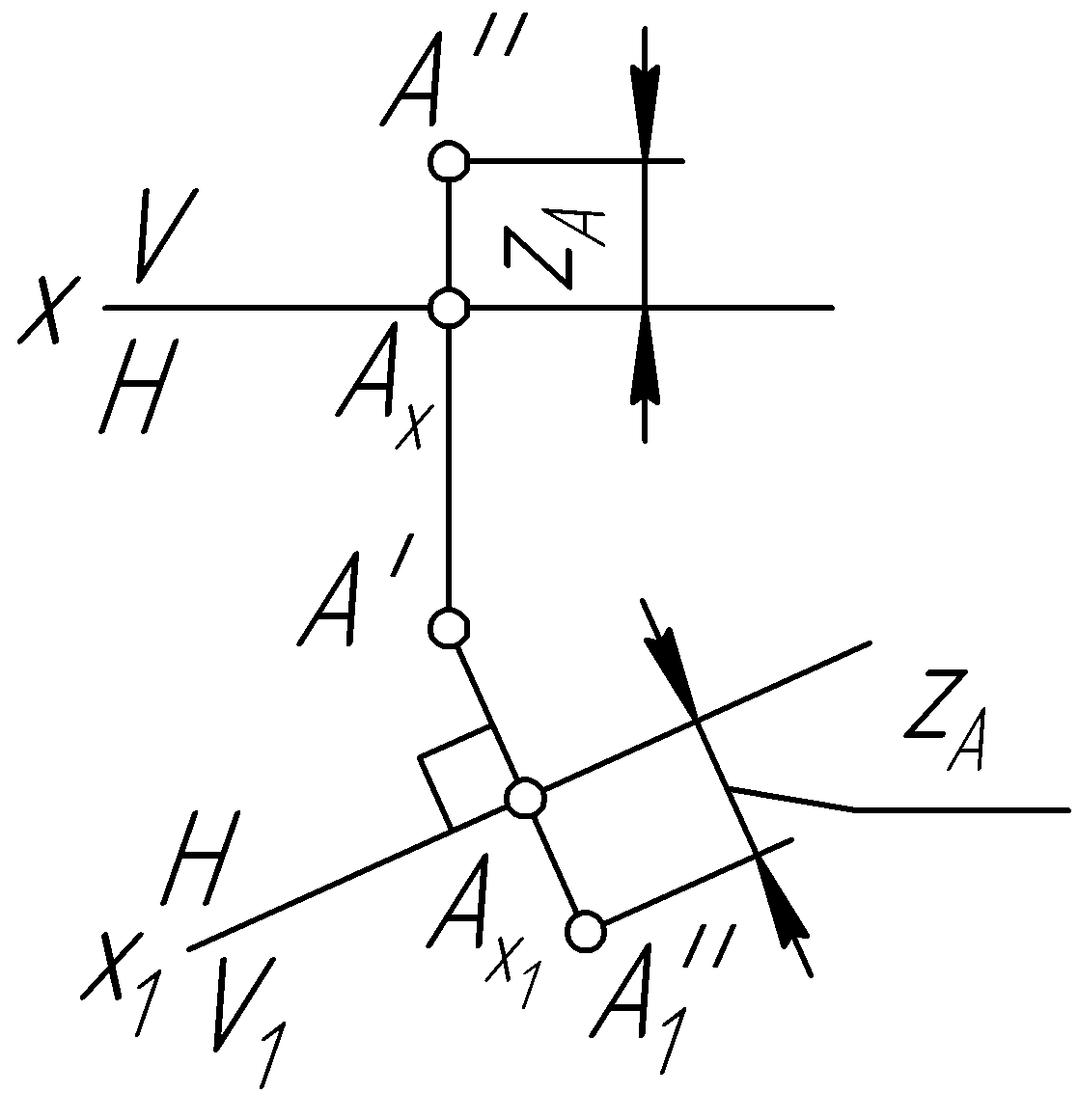
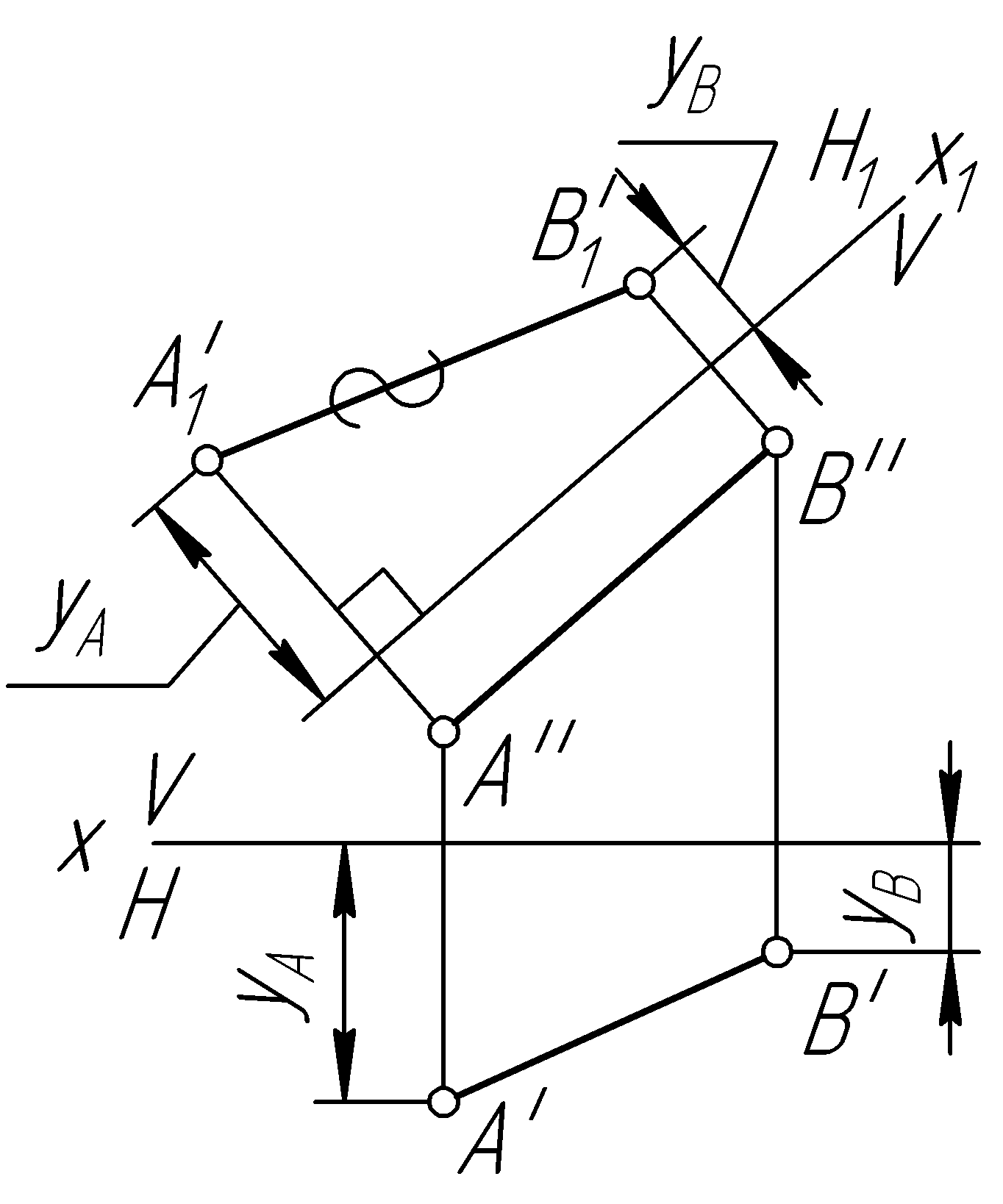
Пример 33. Определить натуральную величину отрезка АВ общего положения (рис. 64, а).
Решение.
Заменим плоскость проекций V
на плоскость
![]() ,
расположив ее параллельно отрезкуАВ
(А'В',
А''В'')
(рис. 64, б).
В новой системе плоскостей проекций
,
расположив ее параллельно отрезкуАВ
(А'В',
А''В'')
(рис. 64, б).
В новой системе плоскостей проекций
![]() отрезокАВ
будет занимать
положение, параллельное плоскости V1,
и
его горизонтальная проекция должна
быть параллельна оси проекций. Поэтому
ось х1
в новой системе плоскостей проекций
отрезокАВ
будет занимать
положение, параллельное плоскости V1,
и
его горизонтальная проекция должна
быть параллельна оси проекций. Поэтому
ось х1
в новой системе плоскостей проекций
![]() строим
параллельно
А'В'.
Откладываем от оси х1
аппликаты
строим
параллельно
А'В'.
Откладываем от оси х1
аппликаты
![]() и
и![]() соответствующих концов отрезка вдоль
линий связи и получаем проекции
соответствующих концов отрезка вдоль
линий связи и получаем проекции![]() и
и![]() .
Соединяем эти точки отрезком прямой и
получаем натуральную величину отрезкаАВ
(А'В',
А''В'').
.
Соединяем эти точки отрезком прямой и
получаем натуральную величину отрезкаАВ
(А'В',
А''В'').
Эту же задачу можно решить, выполнив замену горизонтальной плоскости проекций (рис. 64, в).
|
|
|
Рис. 63
|
|
|
|
а) |
б) |
в)
Рис. 64
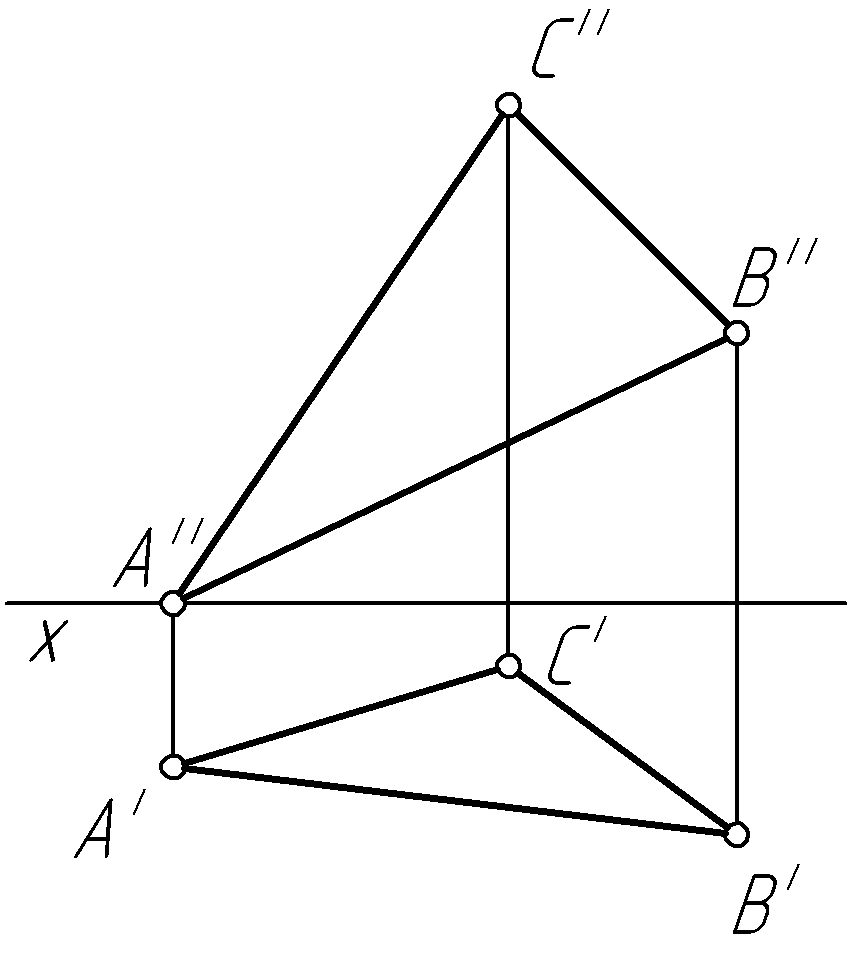
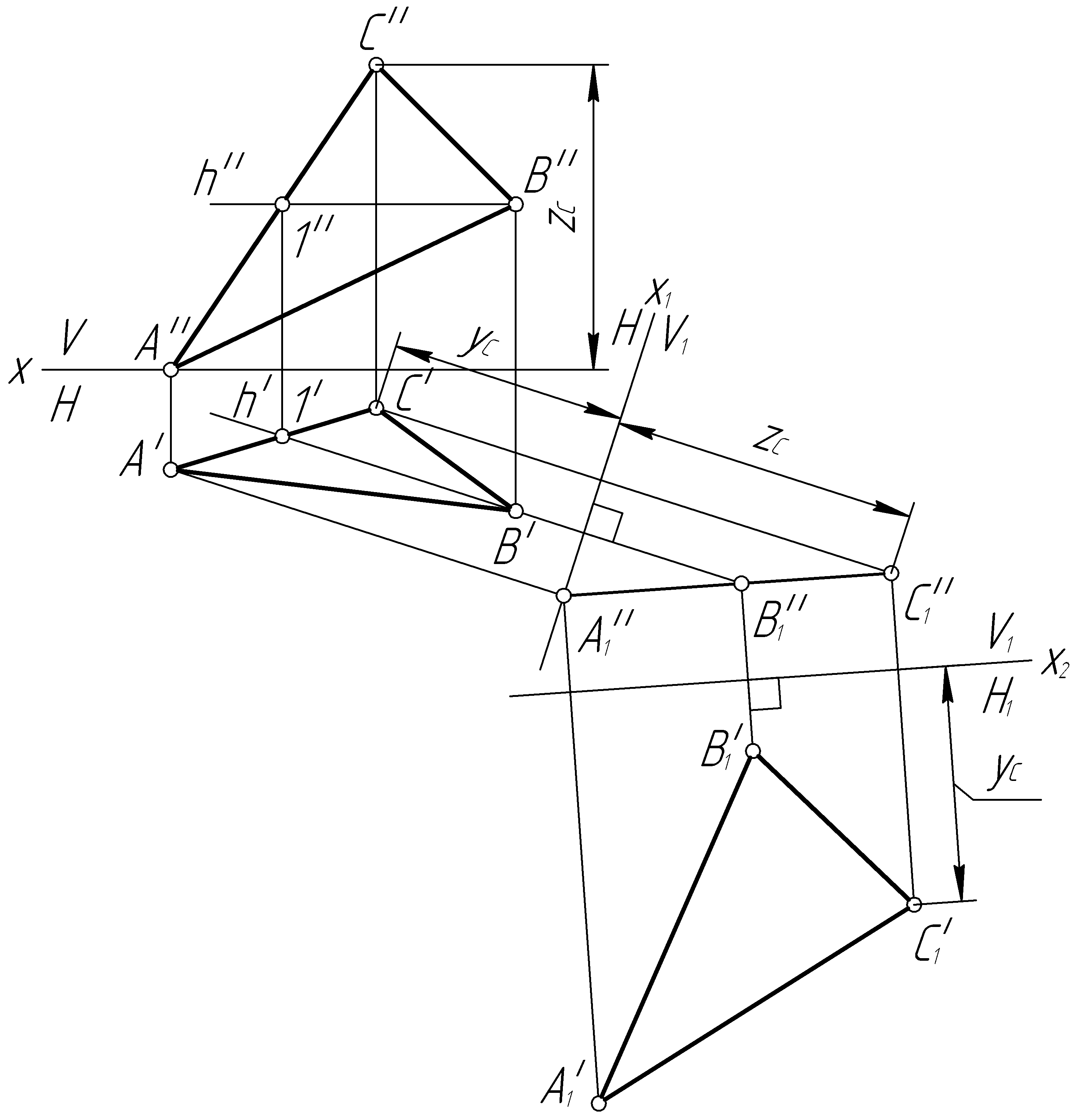
Пример 34. Переменой плоскостей проекций определить натуральную величину треугольника ABC (рис. 65, а).
Решение. Преобразуем систему плоскостей проекций так, чтобы треугольник ABC стал расположен параллельно одной из них (рис. 65, б).
Проведем в
плоскости треугольника горизонталь
h
(![]() ,
,![]() )
и заменим плоскость проекцийV
плоскостью
)
и заменим плоскость проекцийV
плоскостью
![]() ,
перпендикулярной горизонталиh
(х1
,
перпендикулярной горизонталиh
(х1
![]()
![]() ),
а следовательно, и треугольникуABC.
При этом сохраняются аппликаты точек
А,
В
и С.
Новая фронтальная проекция треугольника
преобразуется в прямую линию
),
а следовательно, и треугольникуABC.
При этом сохраняются аппликаты точек
А,
В
и С.
Новая фронтальная проекция треугольника
преобразуется в прямую линию
![]() .
.
Затем введем
параллельно плоскости треугольника и
перпендикулярно
![]() новую горизонтальную плоскость проекций
новую горизонтальную плоскость проекций![]() (строимх2
║
(строимх2
║![]() ),
на которой получим новую горизонтальную
проекцию
),
на которой получим новую горизонтальную
проекцию![]() ,
представляющую собой натуральную
величину треугольникаABC.
При этом остаются неизменными ординаты
точек системы х1
,
представляющую собой натуральную
величину треугольникаABC.
При этом остаются неизменными ординаты
точек системы х1
![]() .
.
|
|
|
а) |
б)
Рис. 65