Тема 1. Общие сведения по геодезии

Лекция 1:

1.1. Предмет и задачи геодезии

Геодезия - это наука, изучающая фигуру и размеры Земли, ее внешнее гравитационное поле, расположение объектов земной поверхности, формы ее рельефа и занимающаяся измерениями в натуре, необходимыми для решения различных инженерных, экономических и др. задач.

Для проведения различных работ, связанных со строительством сооружений необходимо более полное изучение земной поверхности и прежде всего производства измерений на ней, их обработки и составлении карт, планов и профилей, служащих основной геодезической продукцией и дающих представление о форме и размерах всей Земли или отдельных ее частей.

Поэтому в задачу геодезии входит изучение методов:

1) измерения линий и углов на земной поверхности, под землей (в шахтах, тоннелях), над землей (при аэрофотосъемке, при использовании искусственных спутников Земли и космических ракет);

2) математической обработки результатов полевых измерений;

3) графических построений и оформления карт, планов и профилей;

4) использования результатов измерений и графических построений при решении задач промышленного, гражданского, сельскохозяйственного, транспортного, культурного строительства, научных исследований и т.д.

Задачи геодезии решаются путем специальных измерений, называемых геодезическими измерениями, которые выполняются с помощью геодезических инструментов. Геодезические измерения и последующая математическая и графическая обработка их результатов составляют метод решения задачи геодезии.

2. Понятие форме и размерах Земли

При решении многих геодезических задач требуется знать форму и размеры Земли, которая не является правильным геометрическим телом. Предположение о том, что Земля имеет форму шара была высказана древнегреческим ученым Пифагором (VI век до н.э.). Египетский математик и географ Эратосфен (III веке до н.э.) доказал, что Земля имеет сферическую форму, и определил ее радиус.

Е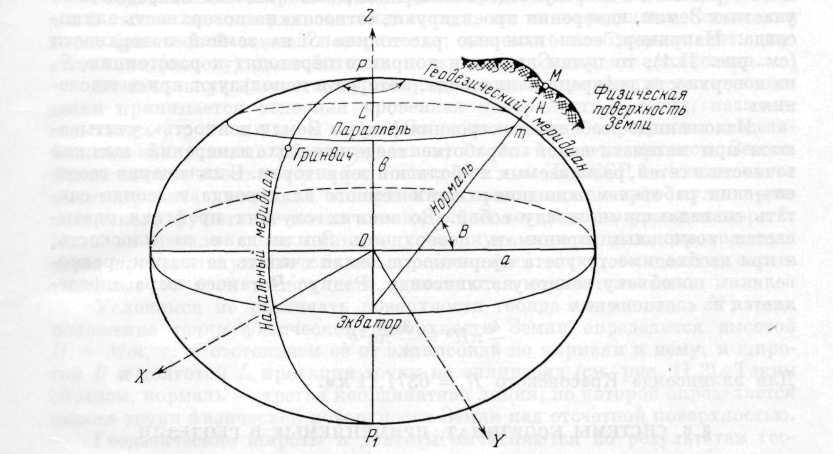сли бы Земля была неподвижным однородным телом и подверженатолько действию внутренних сил тяготения, она имела бы форму шара. Под действием центробежной силы, вызванной вращением вокруг оси с постоянной скоростью, такая Земля приобрела бы форму, сплюснутую по направлению полюсов, т.е. форму сфероида, или эллипсоида вращения.

Рис. 1.1. Земной эллипсоид, геодезические координаты

Поэтому в геодезии за общую фигуру Земли принимается поверхность морей и океанов в спокойном и уравновешенном состоянии, мысленно продолженная под сушей, коротая получила называние уровенной поверхности или геоида. Нетрудно сделать вывод, что правильной математической фигурой, наиболее приближающейся к геоиду, является эллипсоид вращения. Размеры эллипсоида и его форма характеризуются большой а и малой b полуосями (рис. 1.1) или большой полуосью а и полярным сжатием , получаемым из выражения .

Размеры земного эллипсоида неоднократно определялись по результатам геодезических измерений. Значительный вклад в определении размеров эллипсоида был сделан выдающимся русским геодезистом Ф.Н. Красовским (1878—1948 г.), которые были утверждены для геодезических и картографических работ в нашей стране. Эллипсоид Красовского имеет параметры: большая полуось а = 6 378 245 м, малая полуось b = 6 356 863 м, полярное сжатие .

Для того чтобы земной эллипсоид соответствовал геоиду, его надо определенным образом соориентировать в теле Земли. Такой эллипсоид с определенными размерами и определенным образом расположенный в теле Земли получил называние референц-эллипсоида.

С точки зрения инженерно-геодезических работ поверхности земного эллипсоида и геоида можно считать совпадающими между собой. В практических целях оказалось возможным принимать поверхность Земли на ограниченных участках за плоскость, а при необходимости учета сферичности Земли считать ее шаром, равновеликим по объему земному эллипсоиду. Радиус R такого шара для эллипсоида Красовского R = 6371,11 км определяется из соотношения

.