
мет указ числ. ряд
.doc
Федеральное агентство по образованию
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Национальный исследовательский ядерный университет «МИФИ»
Волгодонский инженерно-технический институт - филиал НИЯУ МИФИ
Методические указания к выполнению ИДЗ по теме «Числовые ряды»
ЧИСЛОВОЙ РЯД. СХОДИМОСТЬ ЧИСЛОВОГО РЯДА
Выражение вида
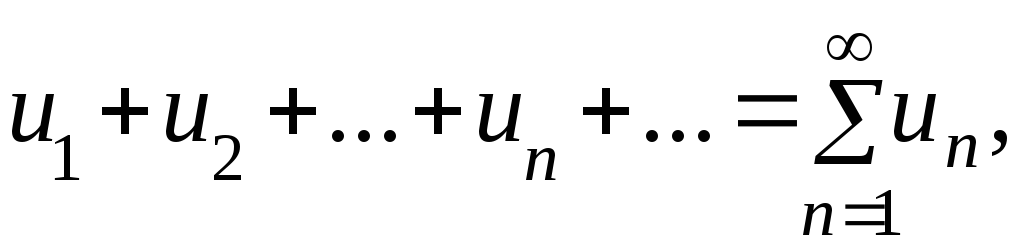 (1)
(1)
где
![]() ─ числа, называется числовым рядом.
─ числа, называется числовым рядом.
Числа
![]() ;
;
![]() ;…;
;…;![]() ;
… ― члены ряда; число
;
… ― члены ряда; число
![]() ― общий член ряда.
― общий член ряда.
Последовательность
![]() ;
;
![]() ;…;
;…;
![]() называется последовательностью частичных
сумм, а
называется последовательностью частичных
сумм, а
![]() ― п-й
частичной суммой ряда.
― п-й
частичной суммой ряда.
Если
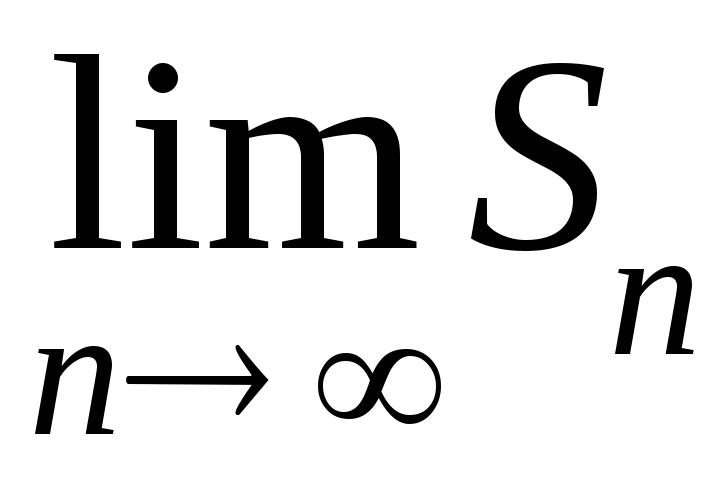 существует и равен числу S,
т.е.
существует и равен числу S,
т.е.
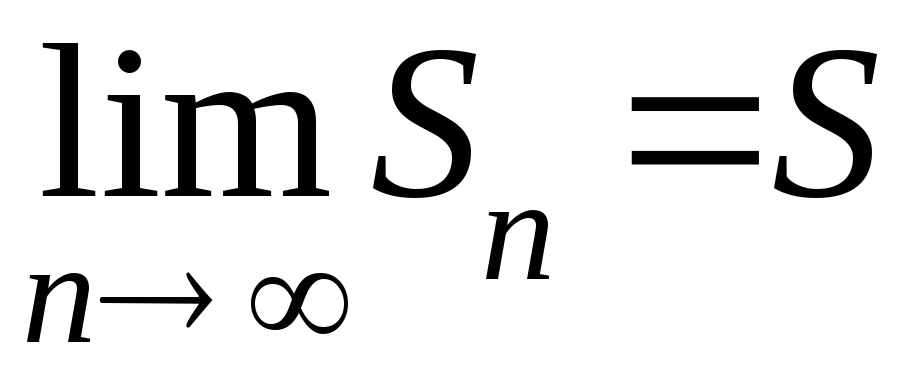 ,
то ряд (1) называется сходящимся, а S
– его суммой. Если
,
то ряд (1) называется сходящимся, а S
– его суммой. Если
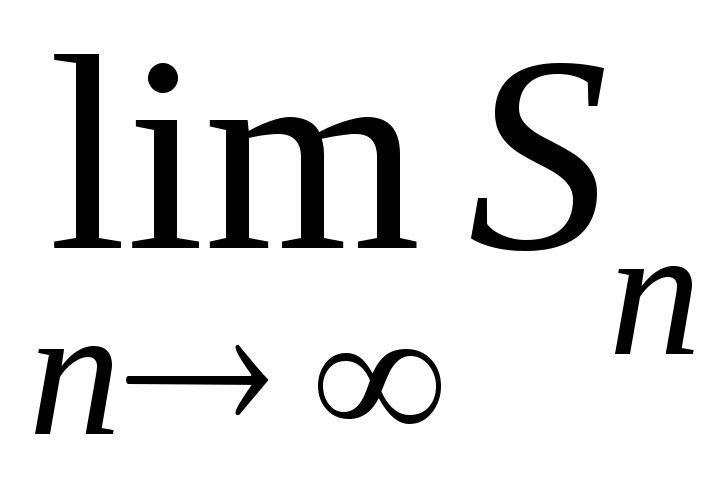 не существует или бесконечен, то ряд
(1) называется расходящимся и суммы не
имеет.
не существует или бесконечен, то ряд
(1) называется расходящимся и суммы не
имеет.
Пример
1. Дан ряд
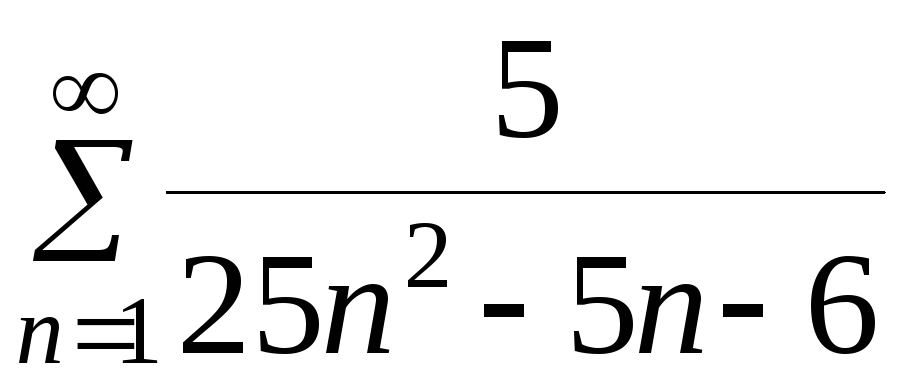 .
Установить сходимость этого ряда и
найти его сумму.
.
Установить сходимость этого ряда и
найти его сумму.
Решение.
Представим общий член ряда
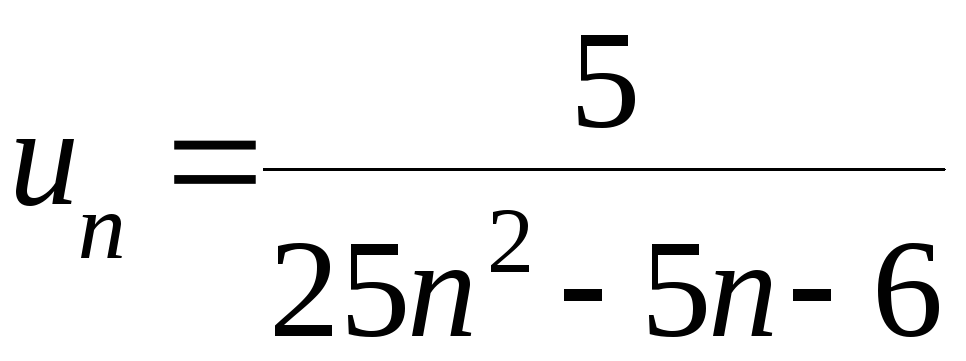 в виде суммы простых дробей методом
неопределённых коэффициентов.
в виде суммы простых дробей методом
неопределённых коэффициентов.
Корни квадратного
трёхчлена
![]() :
:
 ,
,
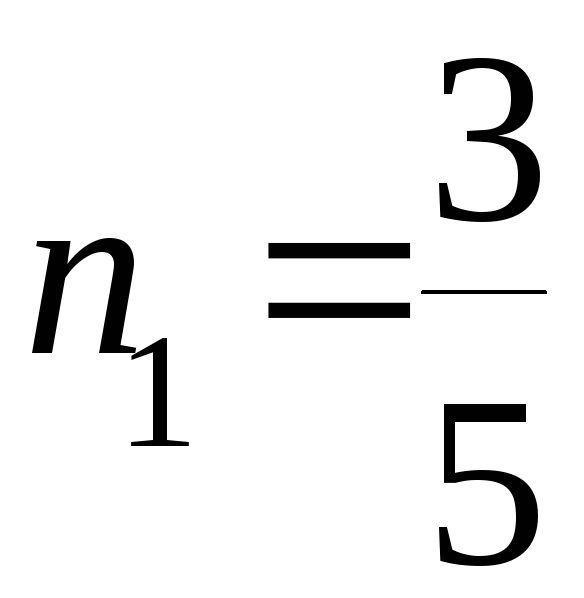 ,
,
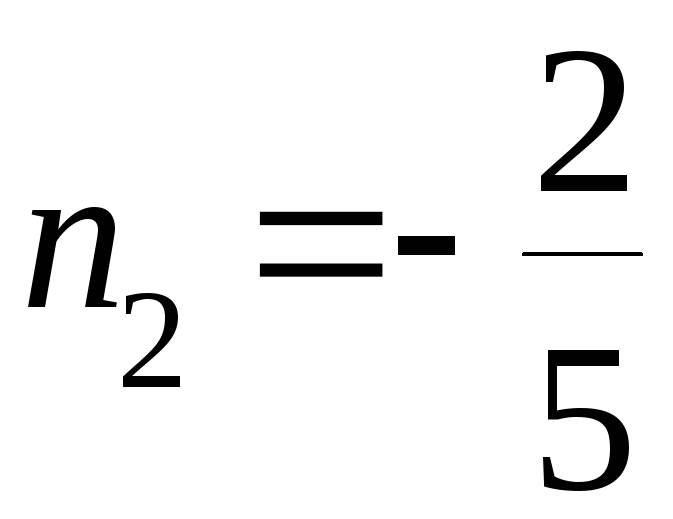 ,
,
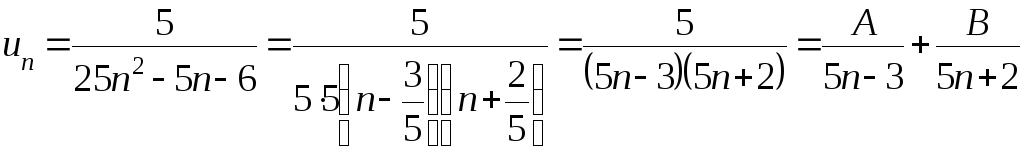 ;
;
![]() ,
,
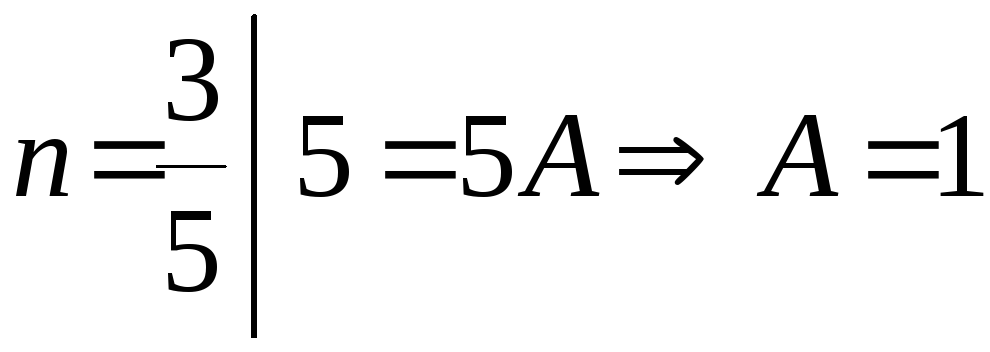 ;
;
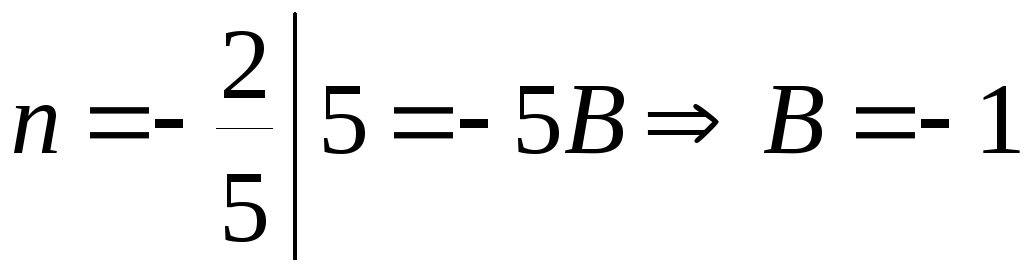 .
.
Следовательно,
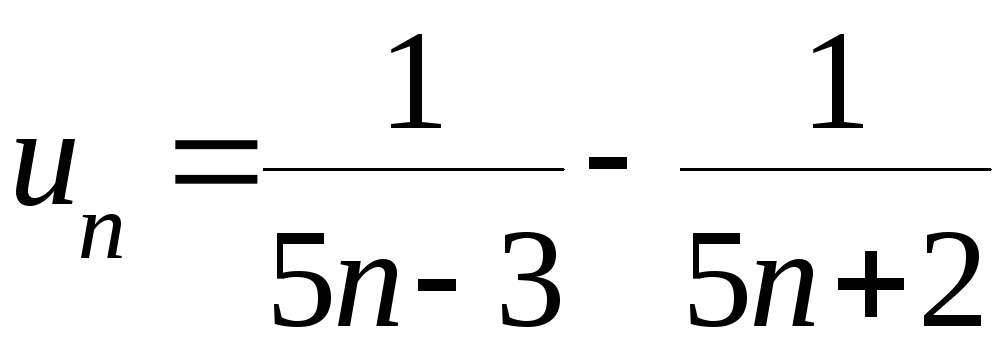 .
.
Запишем п-ю частичную сумму ряда и преобразуем её:
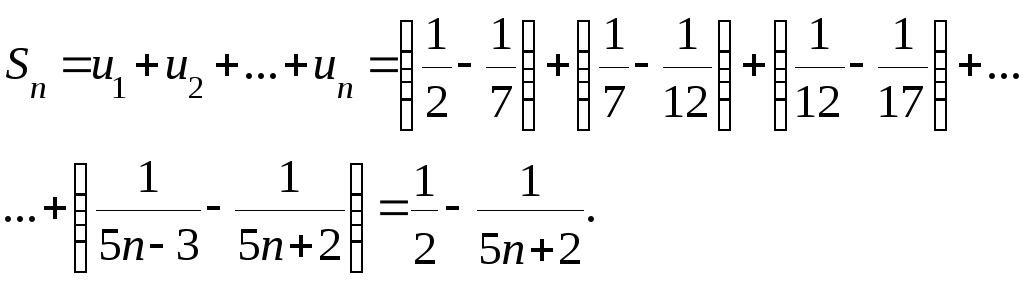
Поскольку

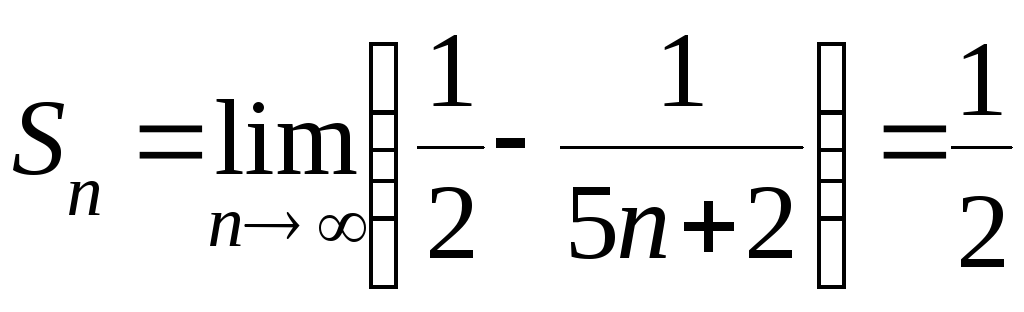 ,
то данный ряд сходится и его сумма S=
,
то данный ряд сходится и его сумма S=![]() .
.
Ответ:
сходится; S=![]() .
.
Необходимый признак сходимости ряда
Если числовой
ряд
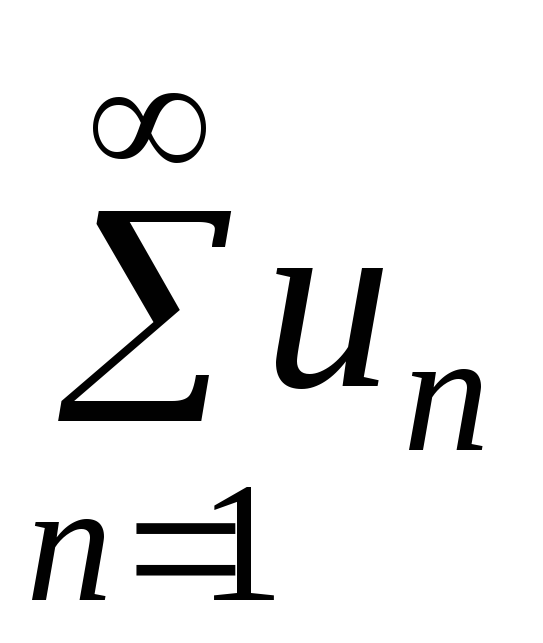 сходится, то
сходится, то
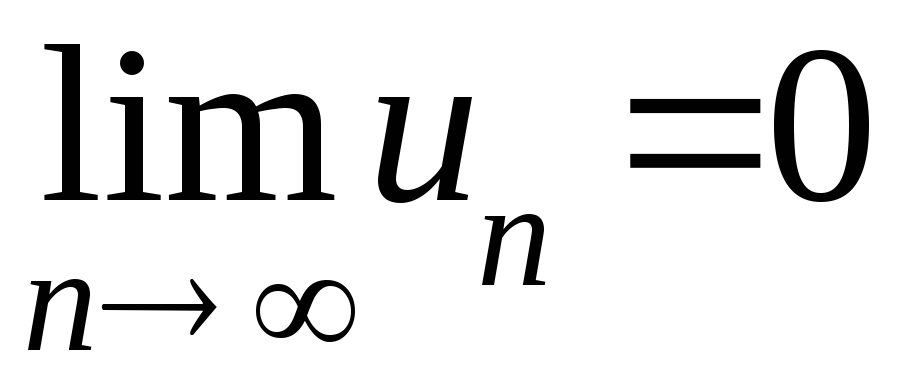 .
.
Замечание. Обратное утверждение не верно.
Достаточный признак расходимости ряда
Если
 ,
то числовой ряд
,
то числовой ряд
![]() расходится.
расходится.
Пример 2. Исследовать ряды на сходимость:
а)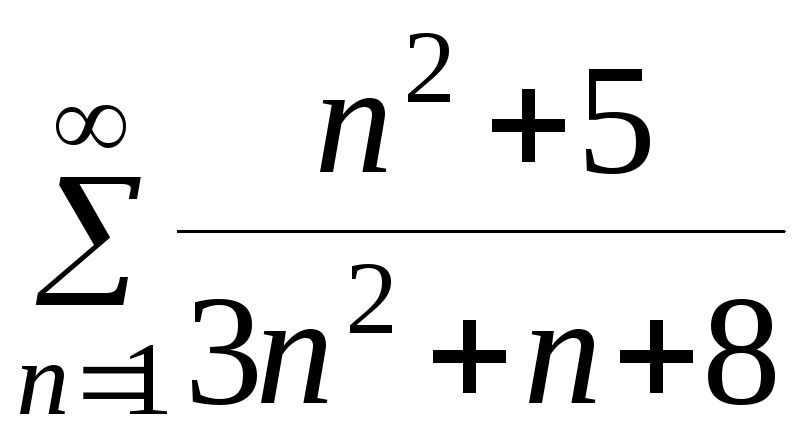 .
.
Решение.
Общий член ряда
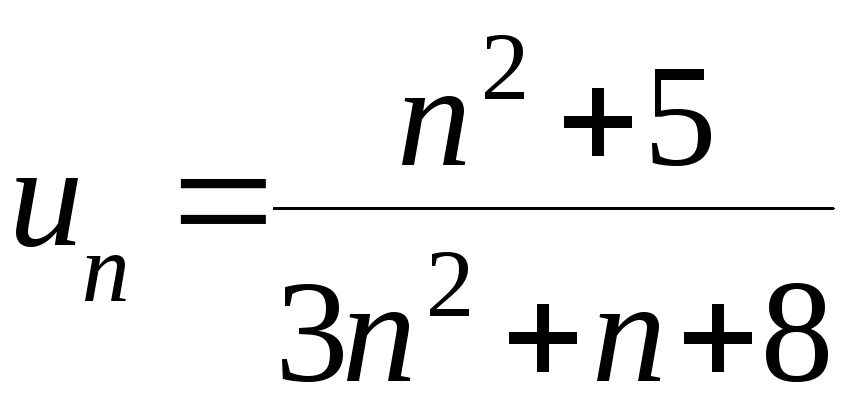 .
Так как
.
Так как
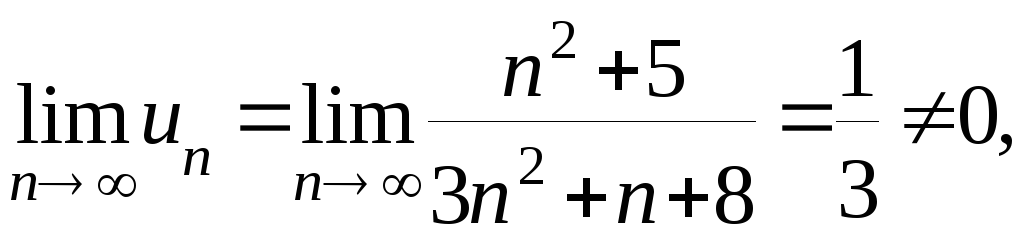 то ряд расходится по достаточному
признаку расходимости.
то ряд расходится по достаточному
признаку расходимости.
Ответ: расходится.
б)
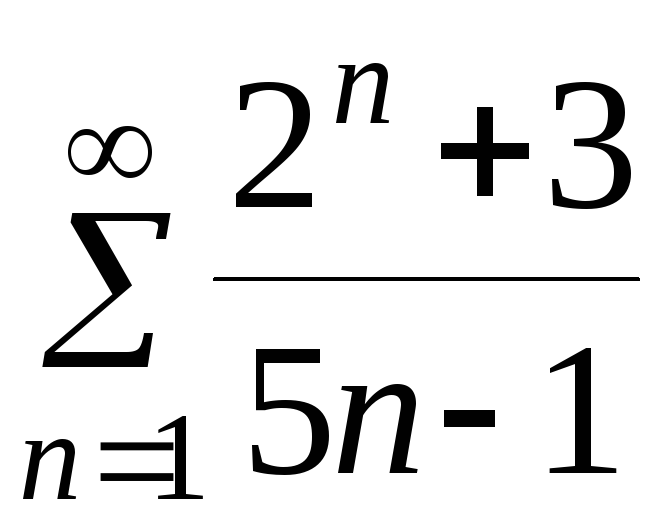 .
.
Решение. Общий
член ряда
 .
.
Так как
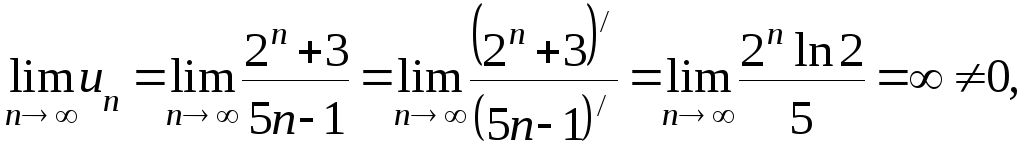 то данный ряд расходится по достаточному
признаку расходимости.
то данный ряд расходится по достаточному
признаку расходимости.
Ответ: расходится.
ПРИЗНАКИ СХОДИМОСТИ ЧИСЛОВЫХ РЯДОВ
С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ
Первый признак сравнения
Даны два ряда
с положительными членами
![]() (1) и
(1) и
![]() (2) и, начиная с некоторого номера
(2) и, начиная с некоторого номера
![]() ,
выполняется неравенство
,
выполняется неравенство
![]() .
Тогда из сходимости ряда (2) следует
сходимость ряда (1); из расходимости ряда
(1) следует расходимость ряда (2).
.
Тогда из сходимости ряда (2) следует
сходимость ряда (1); из расходимости ряда
(1) следует расходимость ряда (2).
Второй признак сравнения (предельный)
Даны два ряда
с положительными членами
![]() (1) и
(1) и
![]() (2) и существует конечный
(2) и существует конечный ,
равный числу А (
,
равный числу А (![]() 0),
тогда ряды (1) и (2) сходятся или расходятся
одновременно.
0),
тогда ряды (1) и (2) сходятся или расходятся
одновременно.
В качестве рядов для сравнения целесообразно выбирать:
1) ряд из членов
геометрической прогрессии
![]() ,
который сходится при
,
который сходится при
![]() и расходится при
и расходится при
![]() .
.
2) обобщенный
гармонический ряд
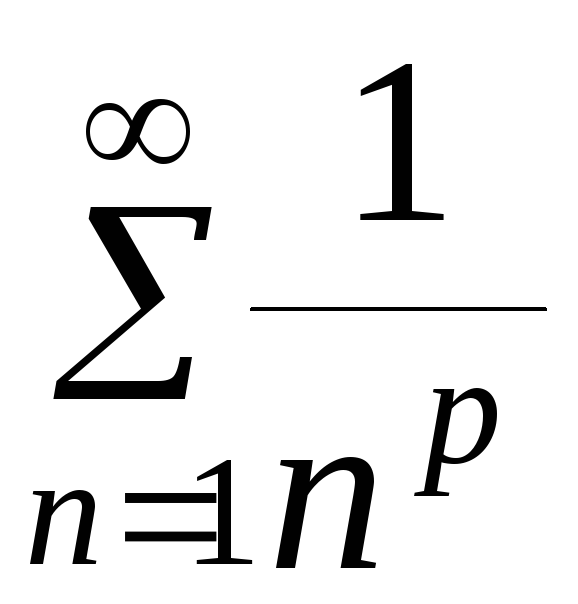 ,
где p>0,
который сходится при
,
где p>0,
который сходится при
![]() и
расходится при
и
расходится при
![]() .
.
Пример 3. Исследовать ряды на сходимость:
а)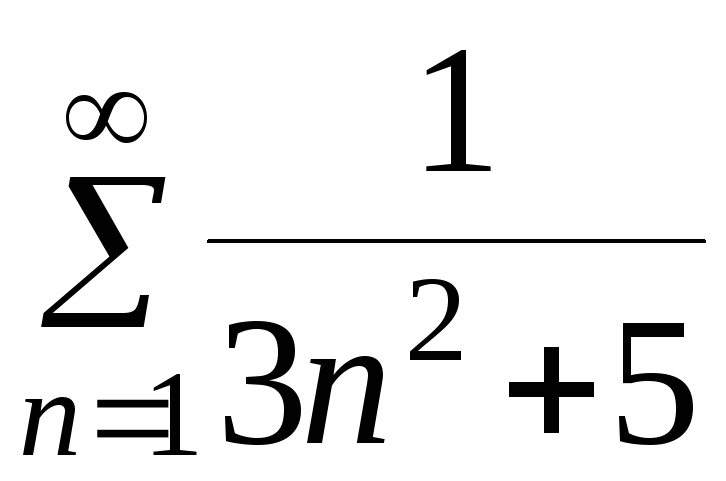 .
.
Решение.
Так как
![]() >
>![]() ,
то, перейдя к обратным выражениям,
получим
,
то, перейдя к обратным выражениям,
получим
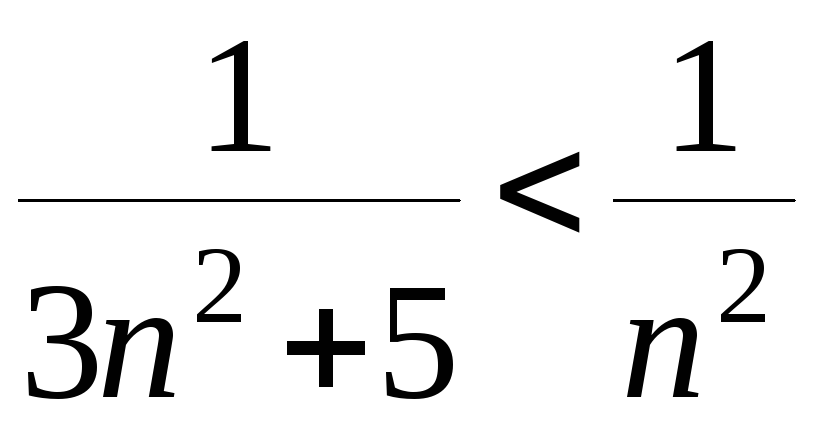 .
Для сравнения возьмем сходящийся
обобщенный гармонический ряд
.
Для сравнения возьмем сходящийся
обобщенный гармонический ряд
![]() .
.
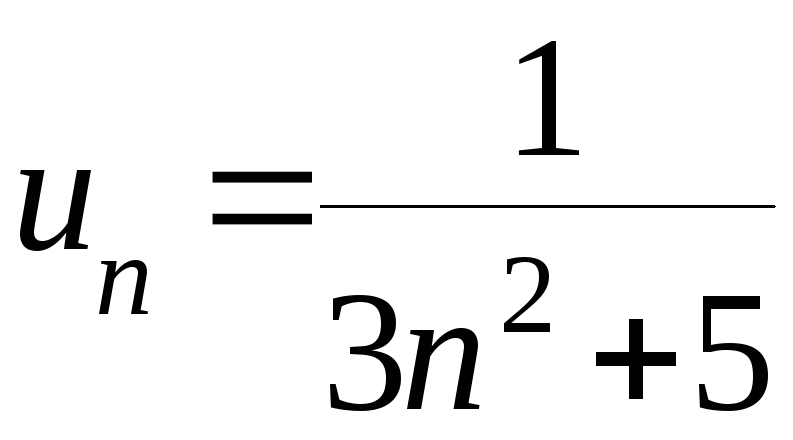 ;
;
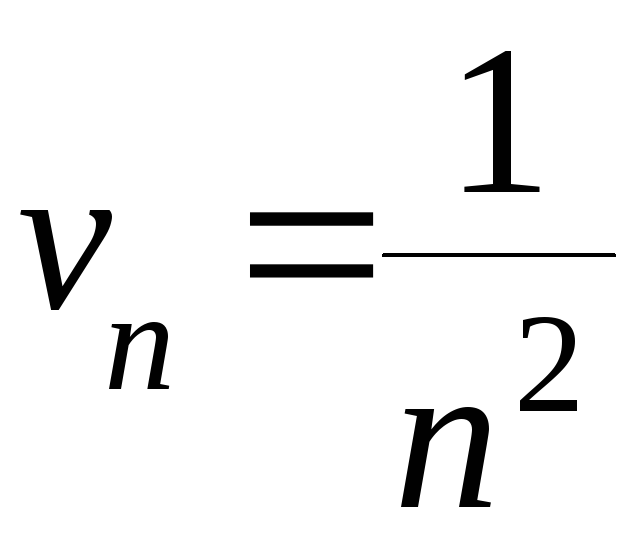 .
Так как
.
Так как
![]() ,
то по первому признаку сравнения из
сходимости
,
то по первому признаку сравнения из
сходимости
![]() следует сходимость ряда
следует сходимость ряда
![]() .
Итак, исходный ряд сходится (его члены
меньше членов сходящегося ряда).
.
Итак, исходный ряд сходится (его члены
меньше членов сходящегося ряда).
Ответ: сходится.
б)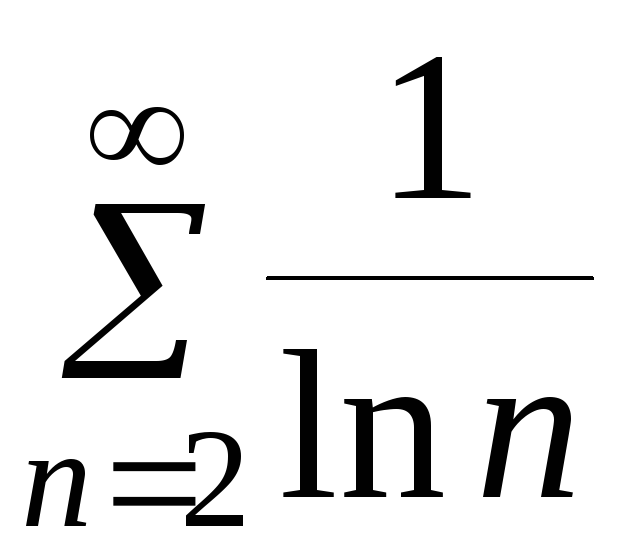 .
.
Решение.
Так как
![]() ,
то, перейдя к обратным выражениям,
получим
,
то, перейдя к обратным выражениям,
получим
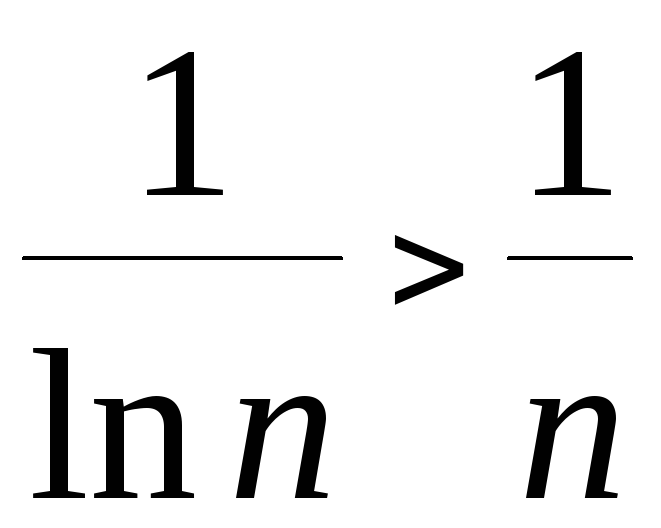 .
Для сравнения возьмем расходящийся
обобщенный гармонический ряд
.
Для сравнения возьмем расходящийся
обобщенный гармонический ряд

![]() .
.
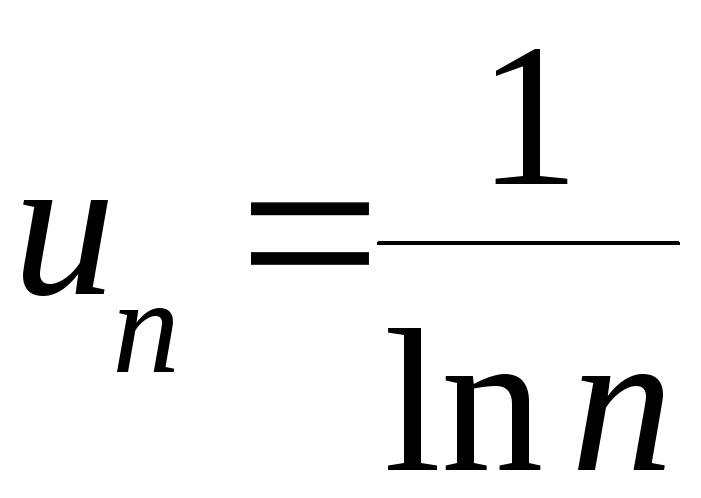 ;
;
 .
.
Так как
![]() ,
то по первому признаку сравнения из
расходимости
,
то по первому признаку сравнения из
расходимости
![]() следует расходимость ряда
следует расходимость ряда
![]() .
Итак, исходный ряд расходится (его члены
больше членов расходящегося ряда).
.
Итак, исходный ряд расходится (его члены
больше членов расходящегося ряда).
Ответ: расходится.
в)
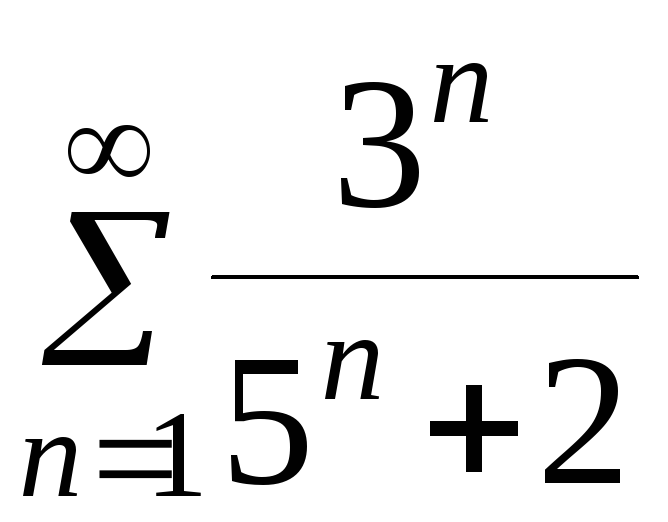 .
.
Решение. Так
как
![]() ,
то, перейдя к обратным выражениям и
домножив обе части неравенства на
,
то, перейдя к обратным выражениям и
домножив обе части неравенства на
![]() ,
получим
,
получим
 .
Для сравнения возьмём сходящийся ряд
из членов геометрической прогрессии
.
Для сравнения возьмём сходящийся ряд
из членов геометрической прогрессии
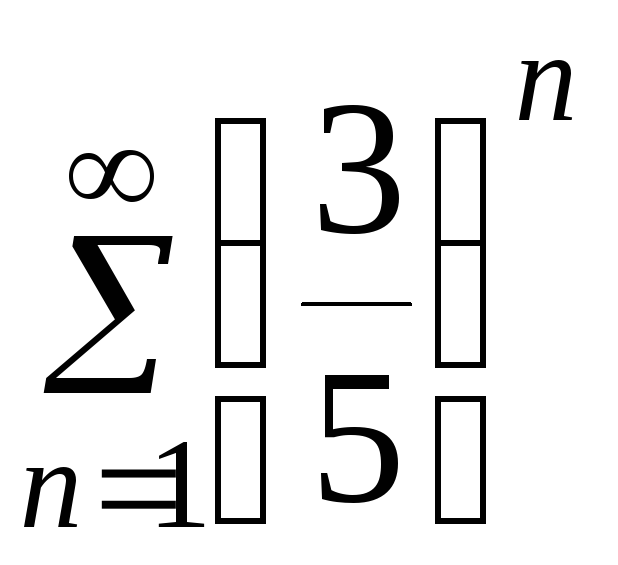 ,
,
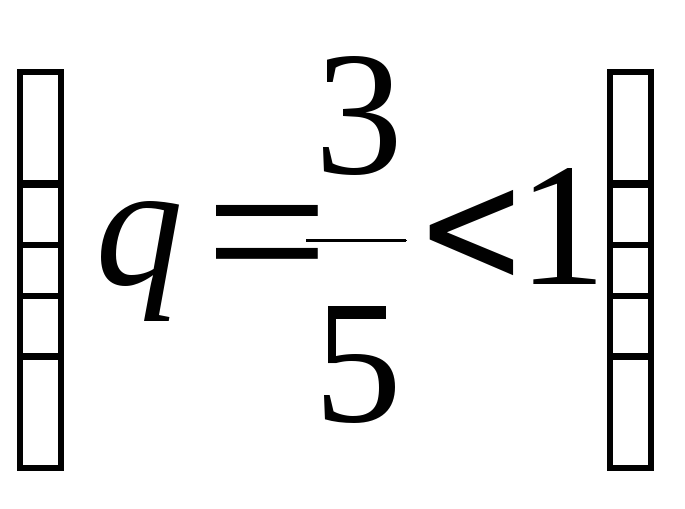 :
:
 ;
;
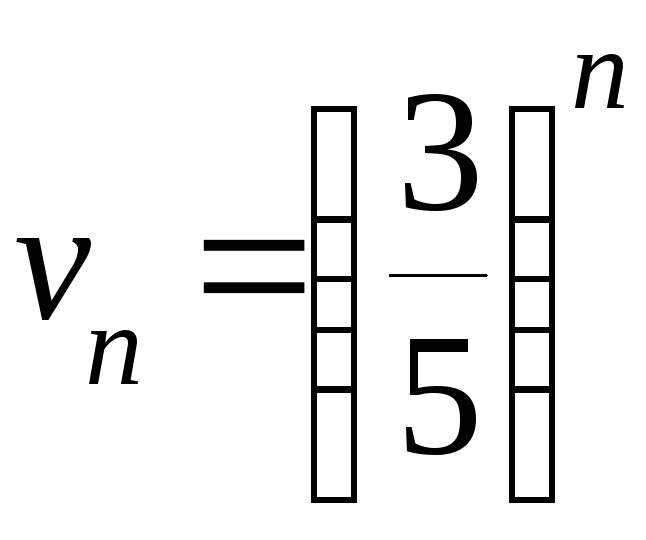 .
.
Так как
![]() ,
то по первому признаку сравнения из
сходимости
,
то по первому признаку сравнения из
сходимости
![]() следует сходимость
следует сходимость
![]() .
.
Исходный ряд сходится (его члены меньше членов сходящегося ряда).
Ответ: сходится.
Пример 4. Исследовать ряды на сходимость:
а)
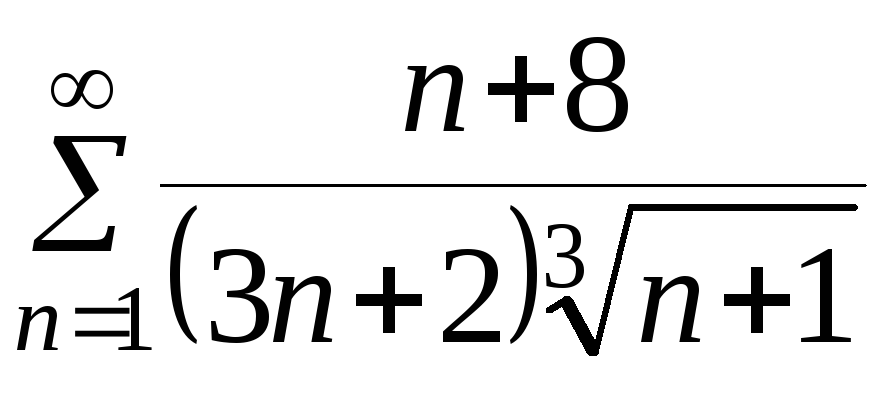 .
.
Решение. Общий
член ряда
 .
.
Для сравнения
возьмём расходящийся обобщенный
гармонический ряд
 (
( )
с общим членом
)
с общим членом
 .
.
Вычислим

Так как этот предел
– число (![]() 0),
то оба ряда расходятся одновременно по
второму признаку сравнения.
0),
то оба ряда расходятся одновременно по
второму признаку сравнения.
Ответ: расходится.
б) .
.
Решение. Общий
член ряда
![]()
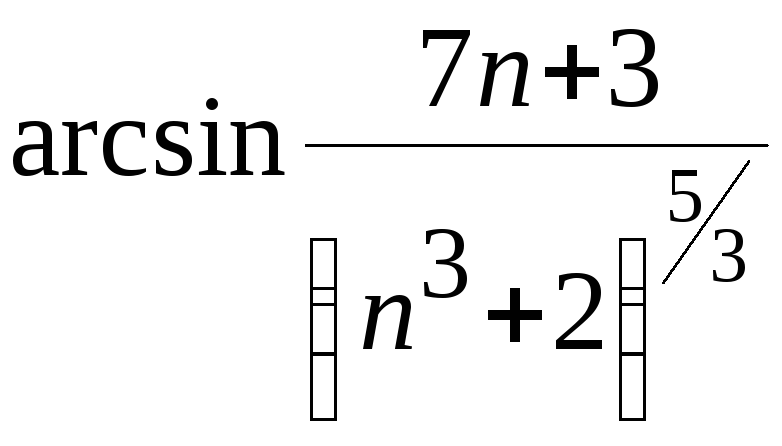 .
.
Сравним ряд со
сходящимся обобщенным гармоническим
рядом с общим членом
с общим членом
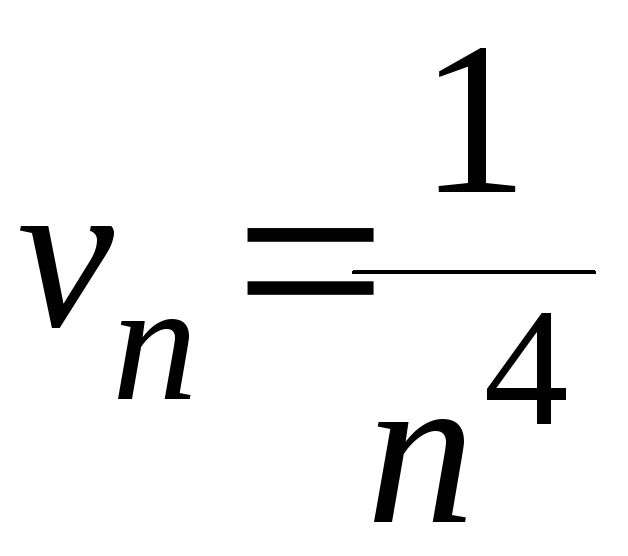 .
.
Вычислим
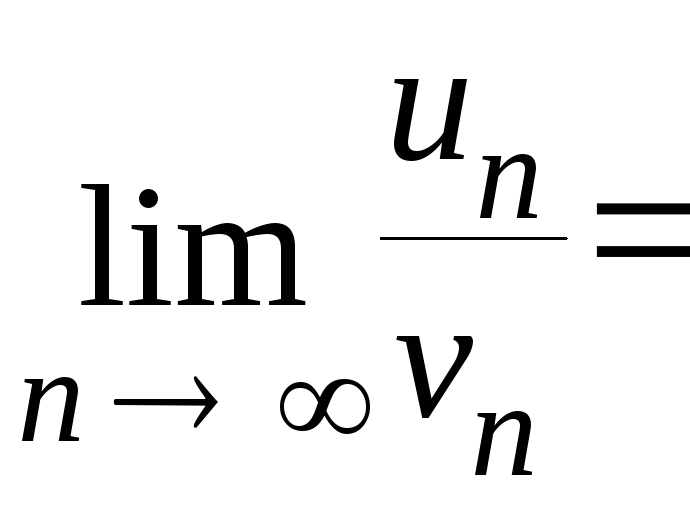
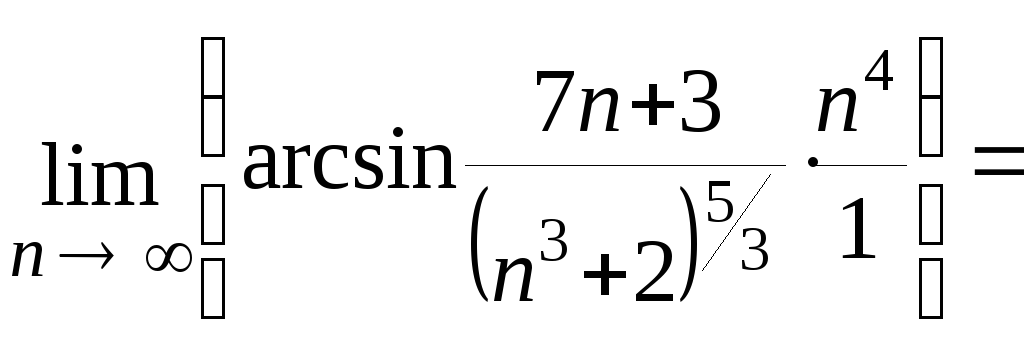
=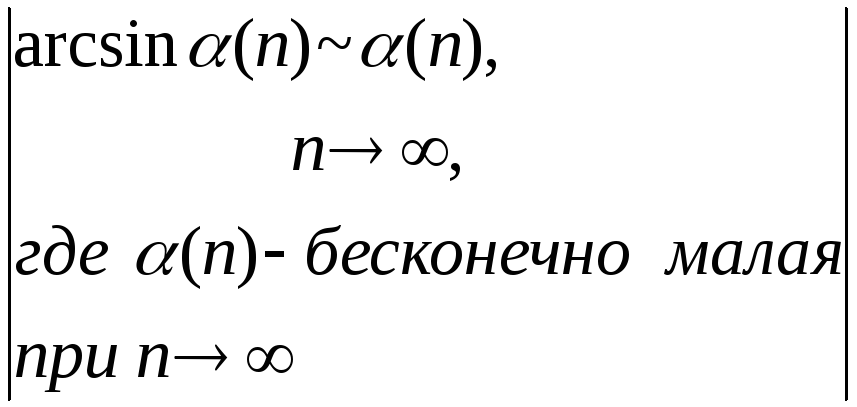 =
=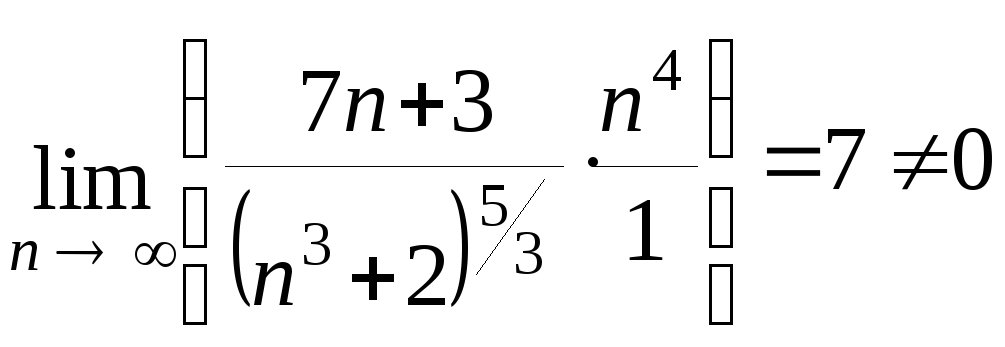 .
.
Так как этот предел
– число (![]() 0), то по второму признаку сравнения оба
ряда сходятся одновременно.
0), то по второму признаку сравнения оба
ряда сходятся одновременно.
Ответ: сходится.
в)
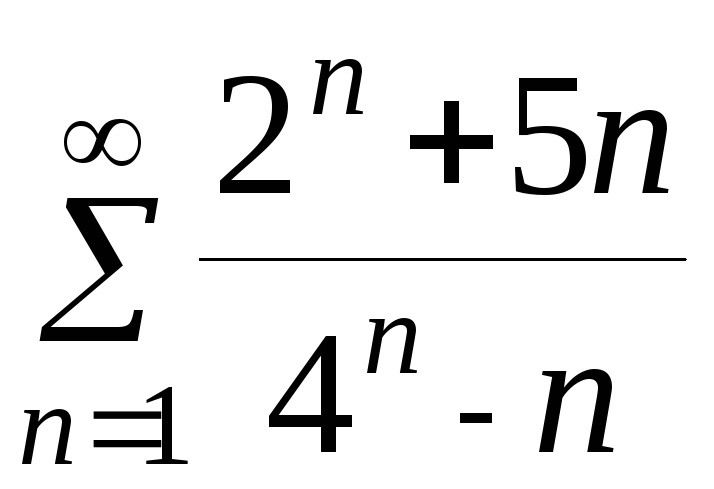 .
.
Решение. Общий
член ряда
 .
.
Сравним этот ряд
со сходящимся рядом из членов геометрической
прогрессии

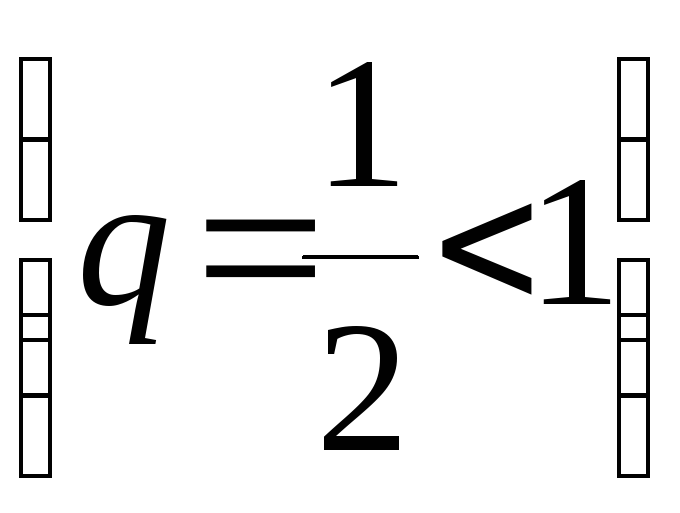 с общим членом
с общим членом
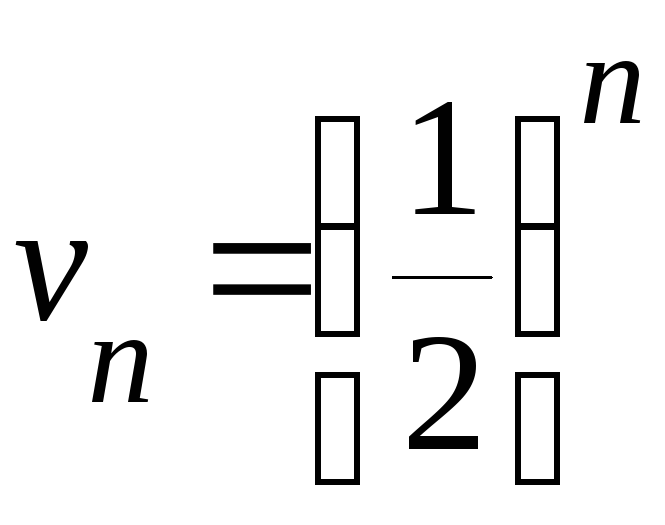 .
.
Вычислим
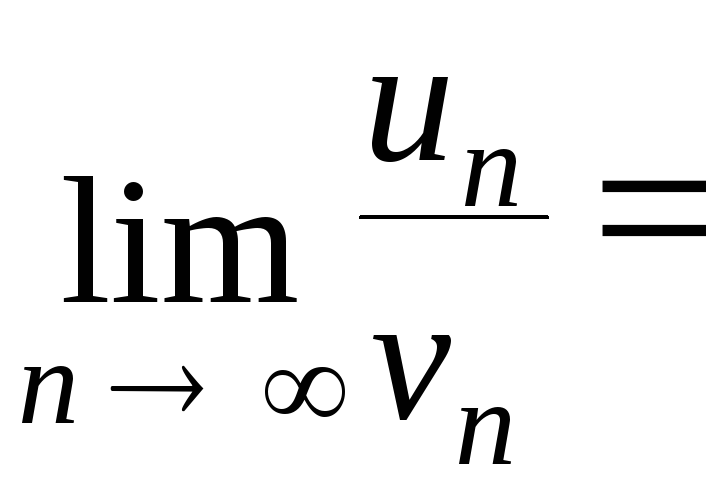

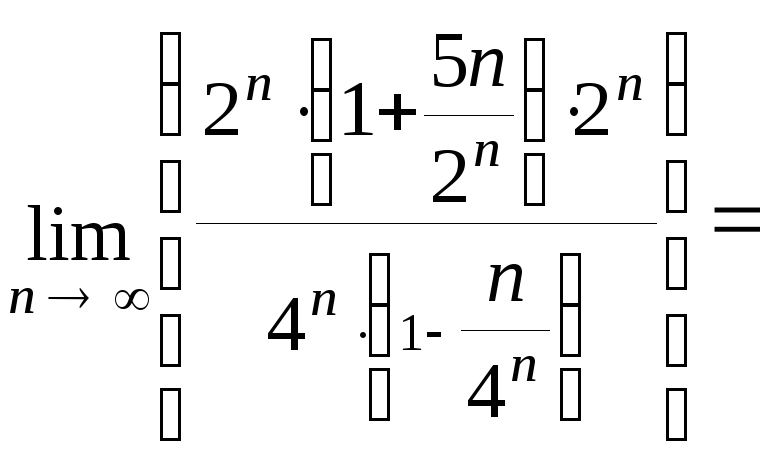
![]()
![]() 0.
0.
Так как этот предел
– число (![]() 0), то по второму признаку сравнения оба
ряда сходятся одновременно.
0), то по второму признаку сравнения оба
ряда сходятся одновременно.
Ответ: сходится.
Признак Даламбера
Пусть дан ряд
с положительными членами
![]() и существует предел
и существует предел
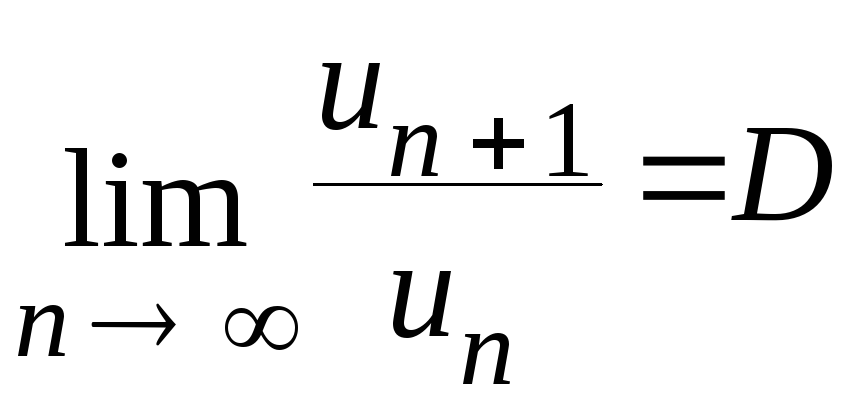 .
.
Тогда: 1) при D < 1 ряд сходится;
2) при D > 1 ряд расходится
( при D = 1 признак Даламбера не дает ответа о сходимости ряда).
Пример 5. Исследовать ряды на сходимость:
а)
 .
.
Решение.
 ;
;
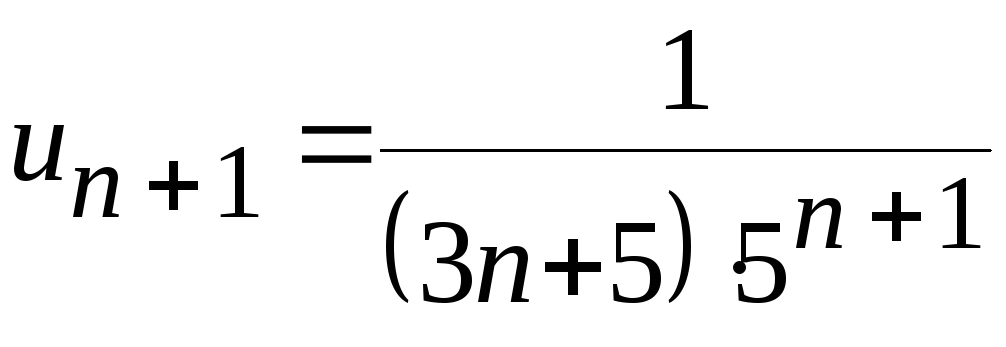 .
.
Вычислим
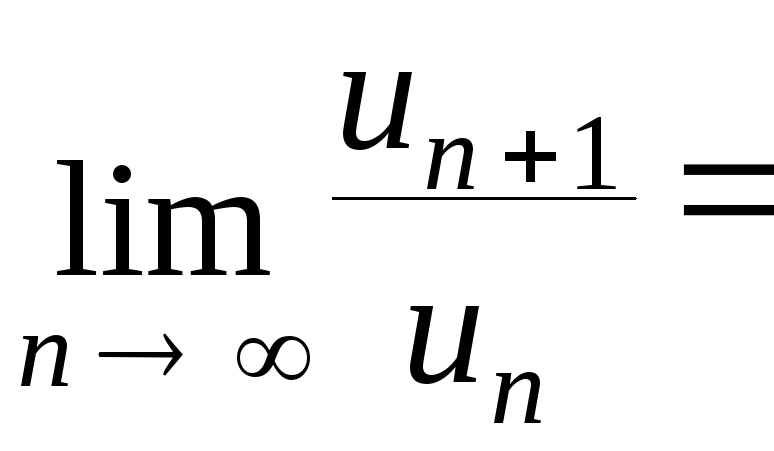
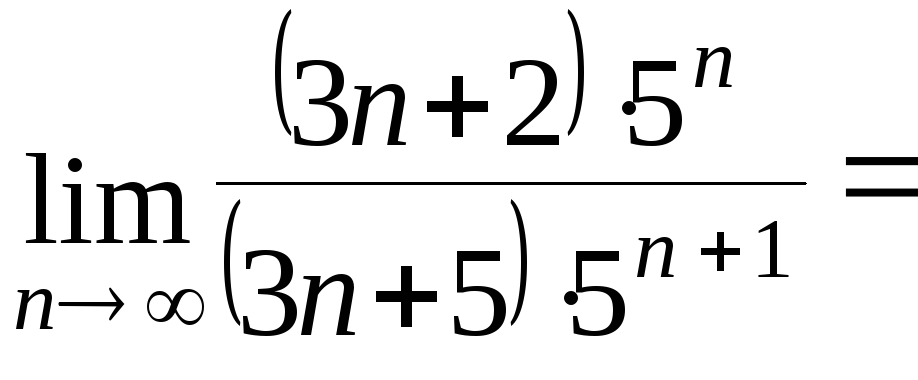
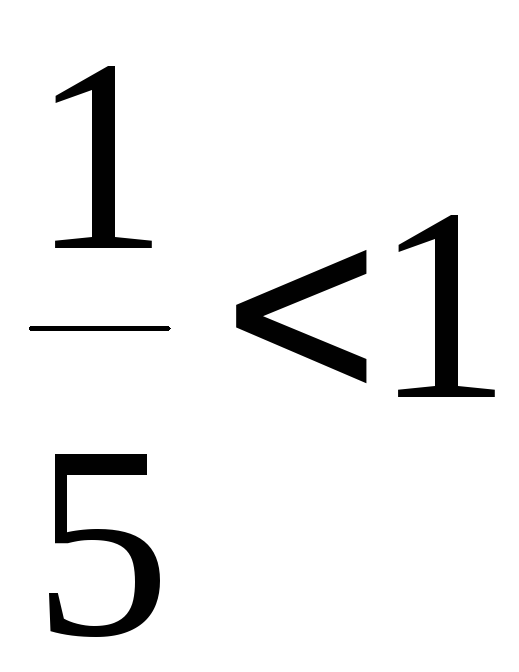 .
.
Следовательно, ряд сходится по признаку Даламбера.
Ответ: сходится.
б)
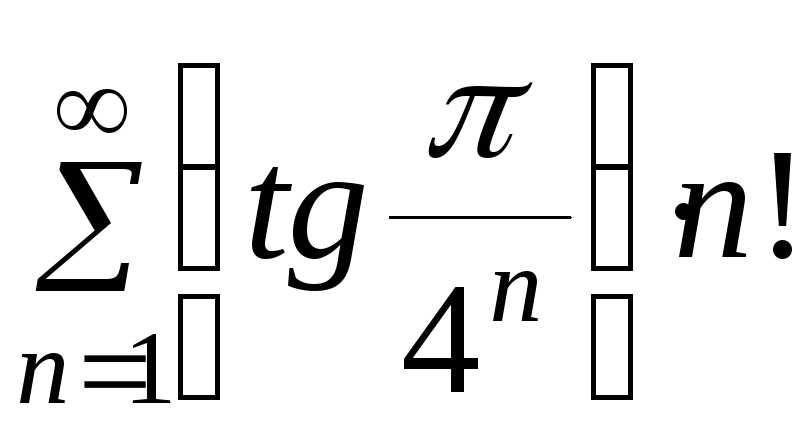 .
.
Решение.
![]()
![]() ;
;
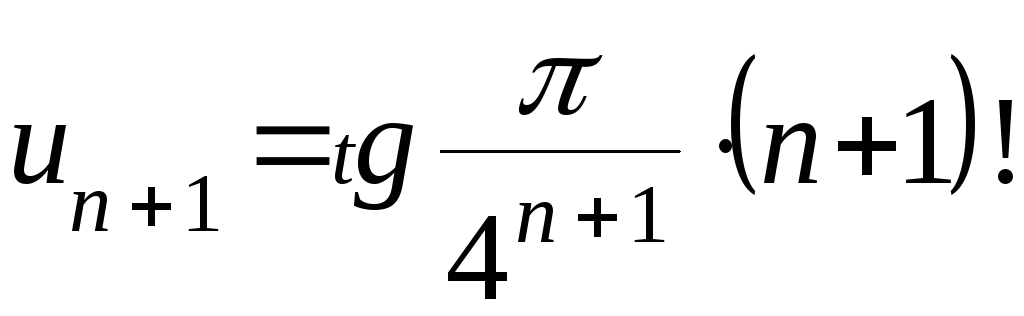 .
.
Вычислим
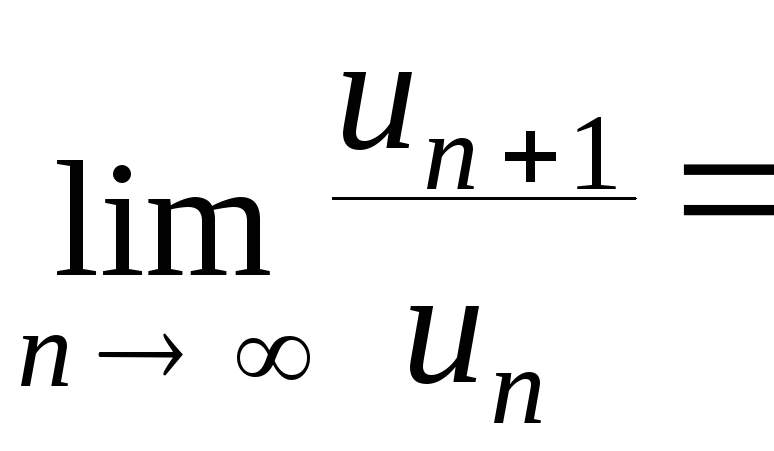
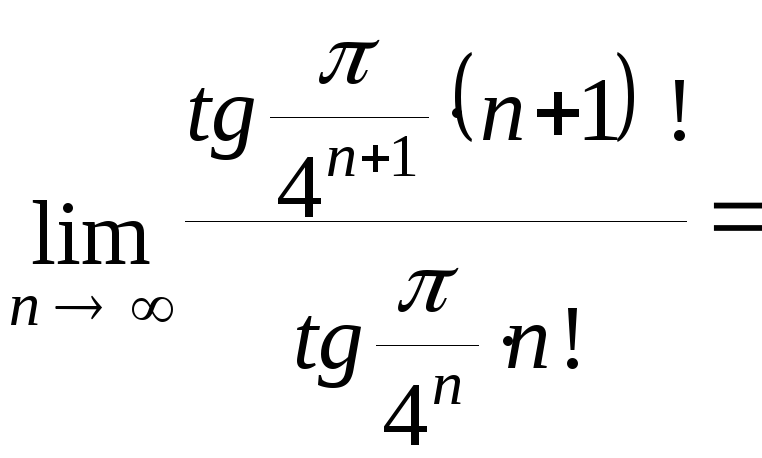
![]()
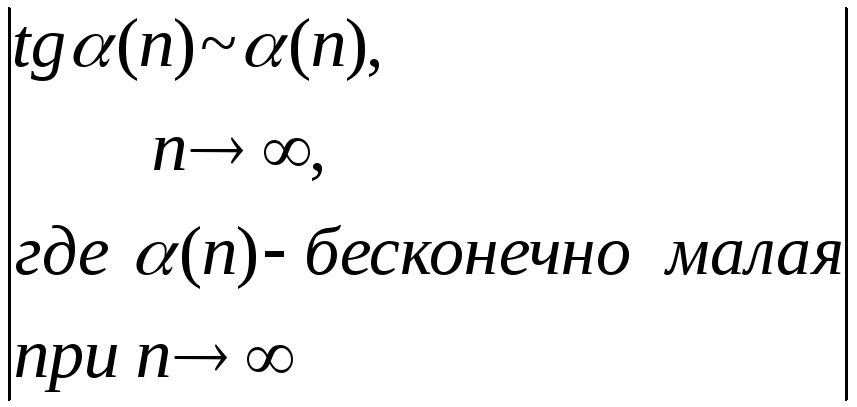
![]()

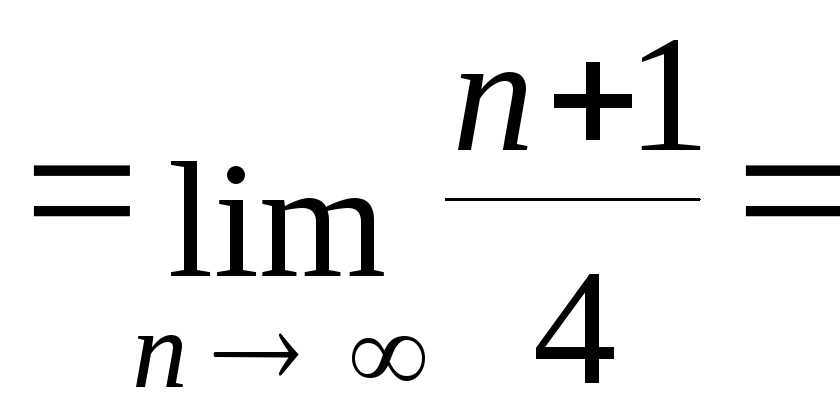
![]() >1.
>1.
Следовательно, ряд расходится по признаку Даламбера.
Ответ: расходится.
в)
 .
.
Решение.
![]()
 ;
;
![]()
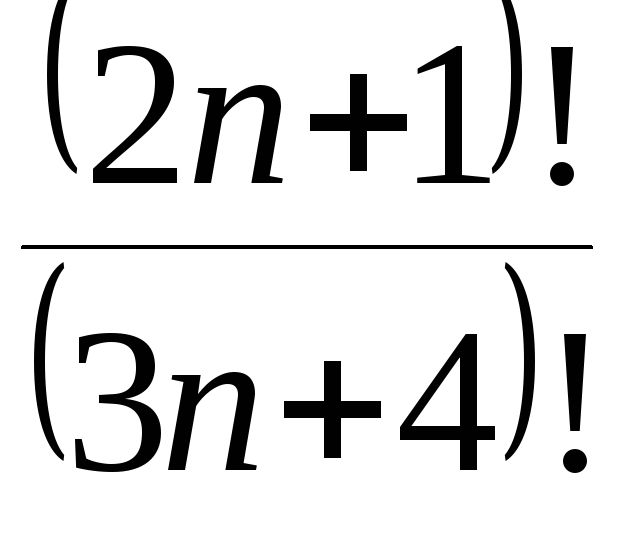 .
.
Вычислим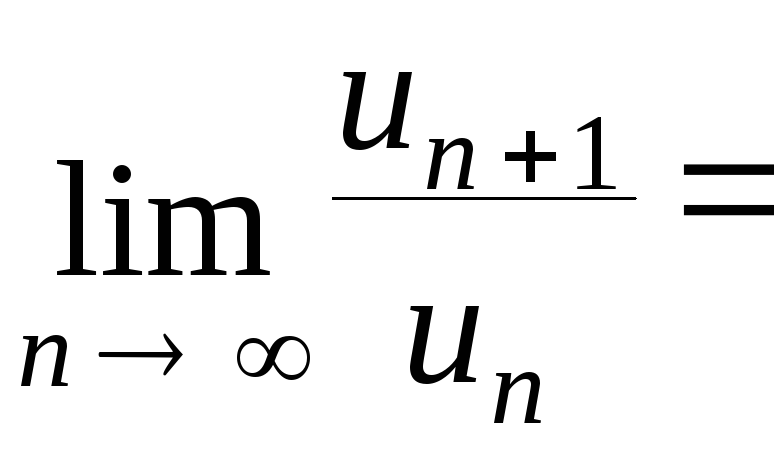

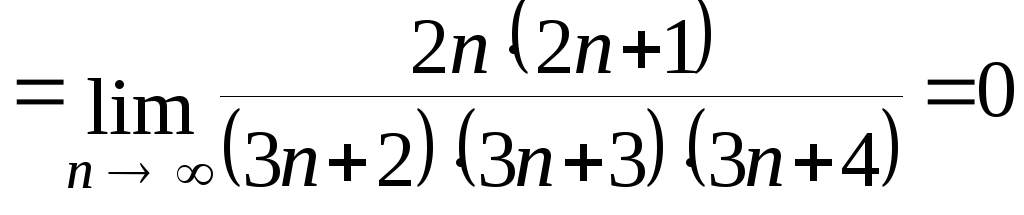
![]() .
.
Следовательно, ряд сходится по признаку Даламбера.
Ответ: сходится.
Радикальный признак Коши
Пусть дан ряд с
положительными членами
![]() и существует предел
и существует предел
![]() .
.
Тогда: 1) при С < 1 ряд сходится;
2) при С > 1 ряд расходится
( при С = 1 признак не дает ответа о сходимости ряда).
Пример 6. Исследовать ряды на сходимость:
а)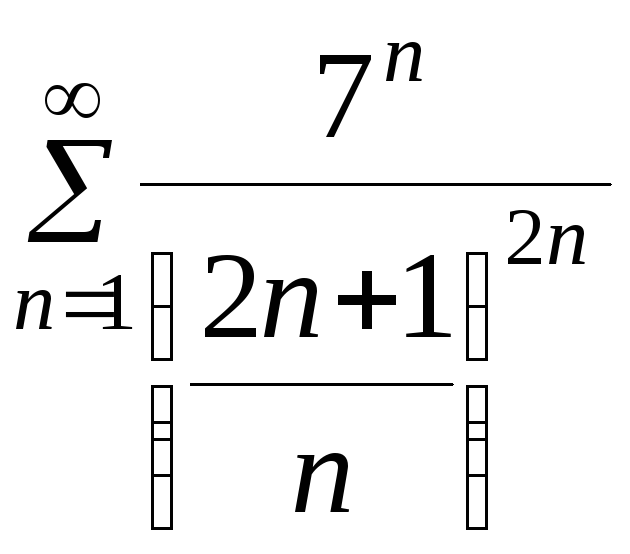 .
.
Решение. Общий
член ряда
![]()
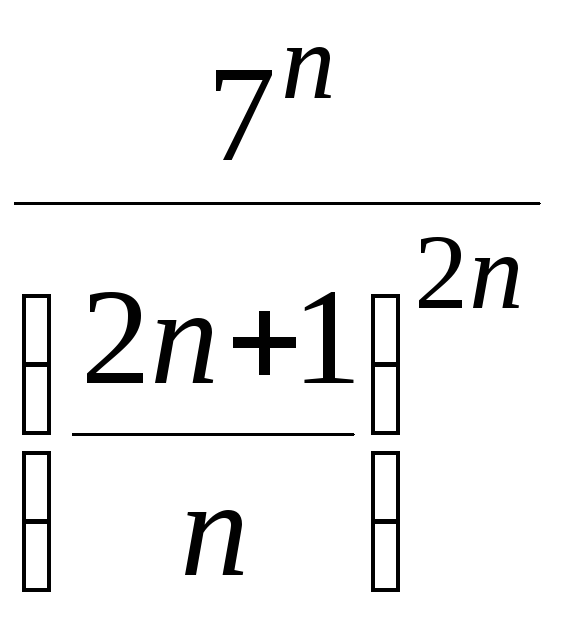
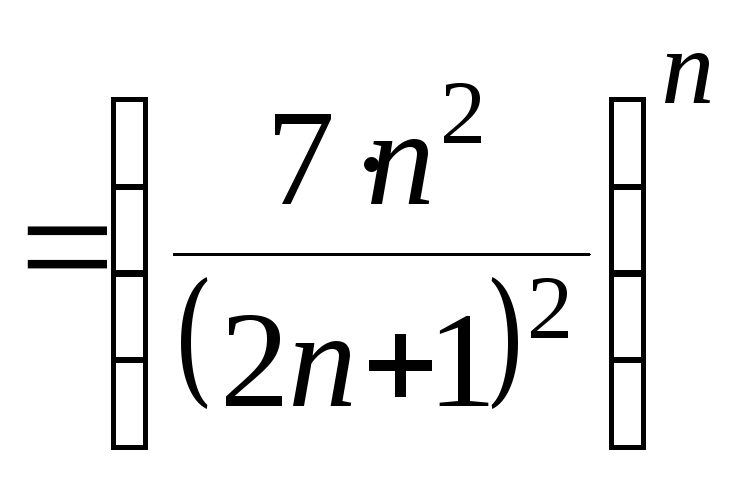 .
.
Вычислим
![]()

![]() >
>![]() .
.
Следовательно, ряд расходится по радикальному признаку Коши.
Ответ: расходится.
б)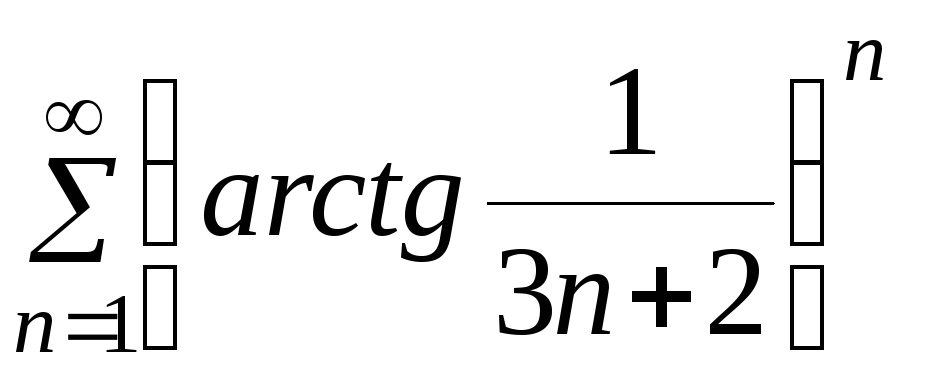 .
.
Решение. Общий
член ряда
![]()
 .
.
Вычислим
![]()
![]()

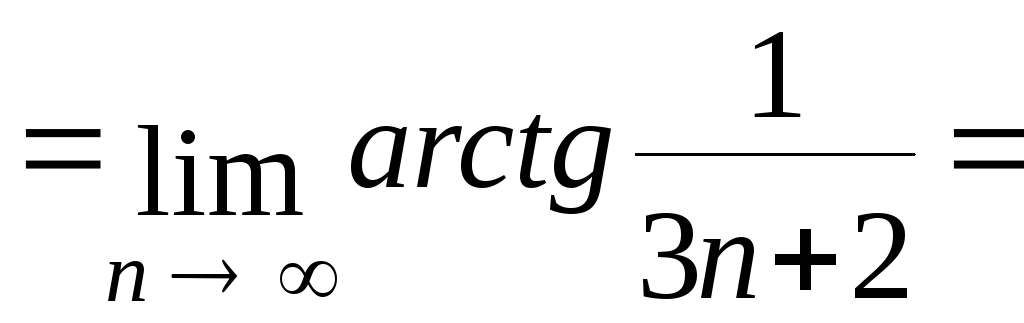
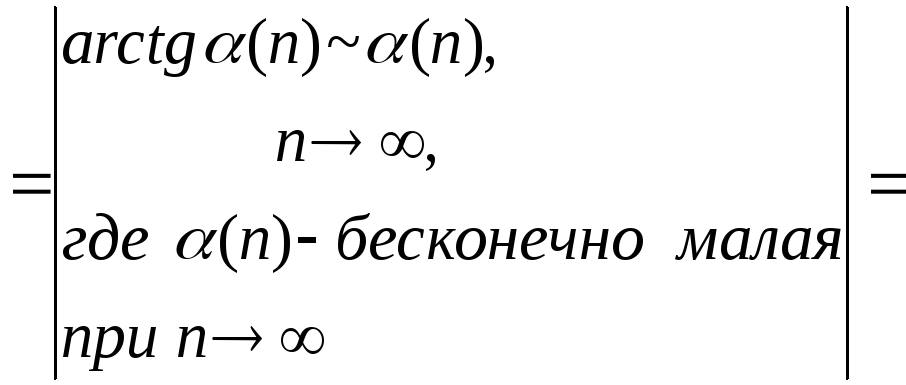
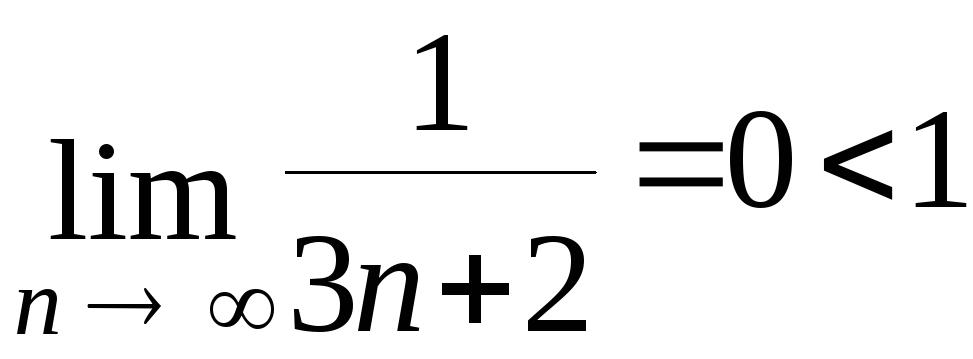 .
.
Следовательно, ряд сходится по радикальному признаку Коши.
Ответ: сходится.
в) .
.
Решение.
Общий член ряда
![]()
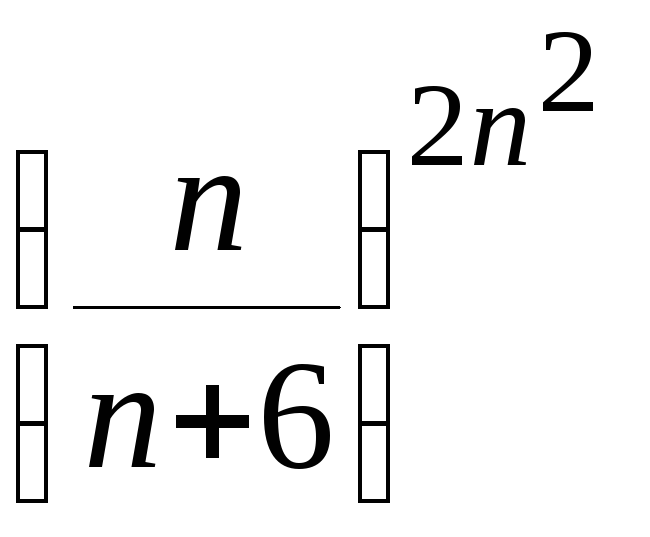
 .
.
Вычислим
![]()
![]()

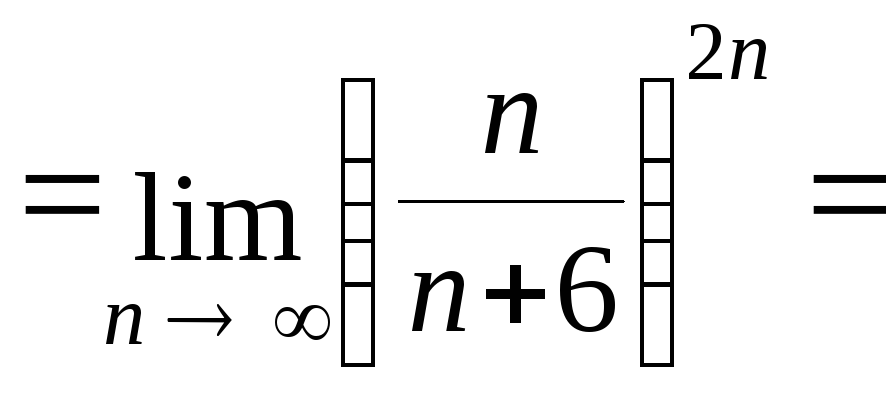
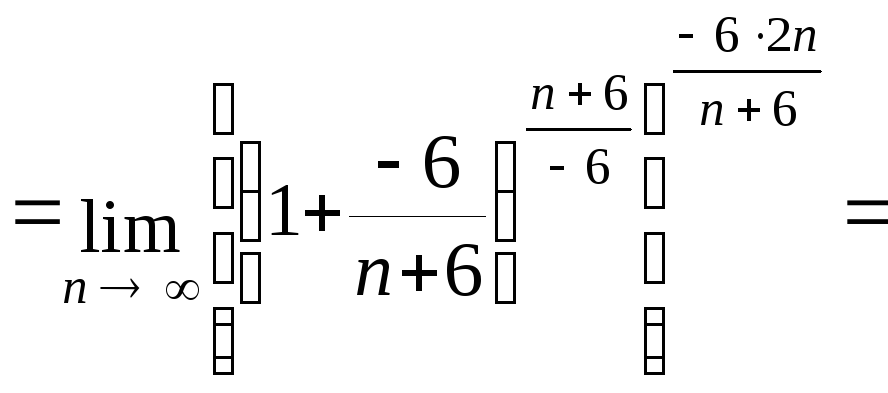
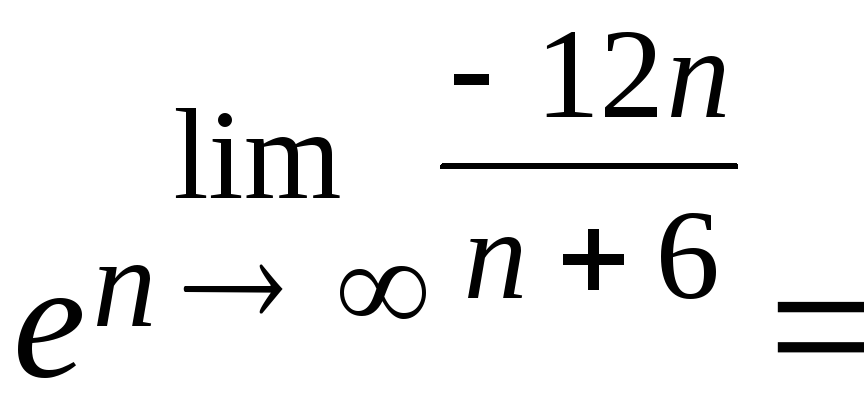
![]()
![]() .
.
Следовательно, ряд сходится по радикальному признаку Коши.
Ответ: сходится.
Интегральный признак Коши
Пусть дан ряд
с положительными членами
![]() такой, что члены ряда монотонно убывают
такой, что члены ряда монотонно убывают
![]() и функция
и функция
![]() ,
непрерывная при
,
непрерывная при
![]() такая, что
такая, что
![]() .
.
Тогда
 и несобственный интеграл
и несобственный интеграл
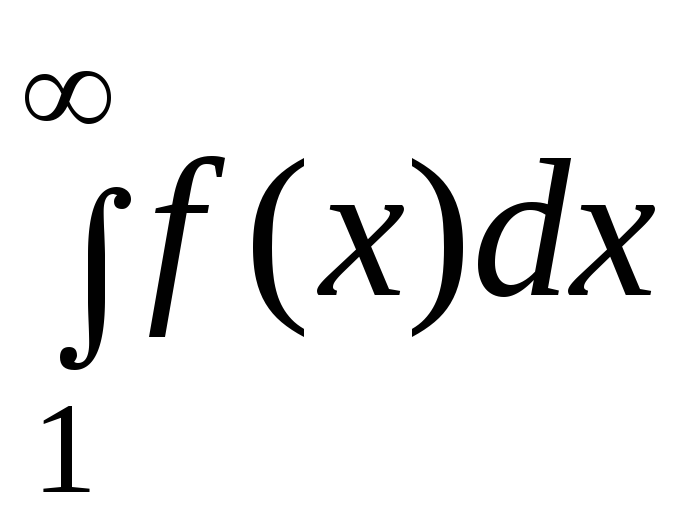 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Пример 7. Исследовать ряды на сходимость:
а)
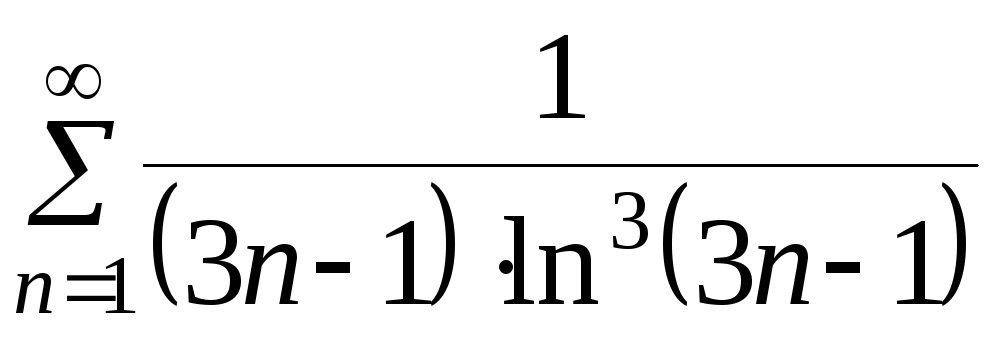 .
.
Решение.
Положим
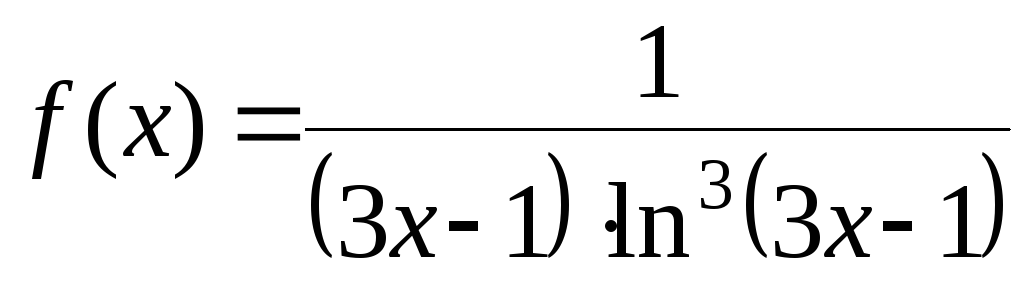 .
Эта функция удовлетворяет всем требованиям
интегрального признака Коши.
.
Эта функция удовлетворяет всем требованиям
интегрального признака Коши.
Рассмотрим несобственный интеграл.
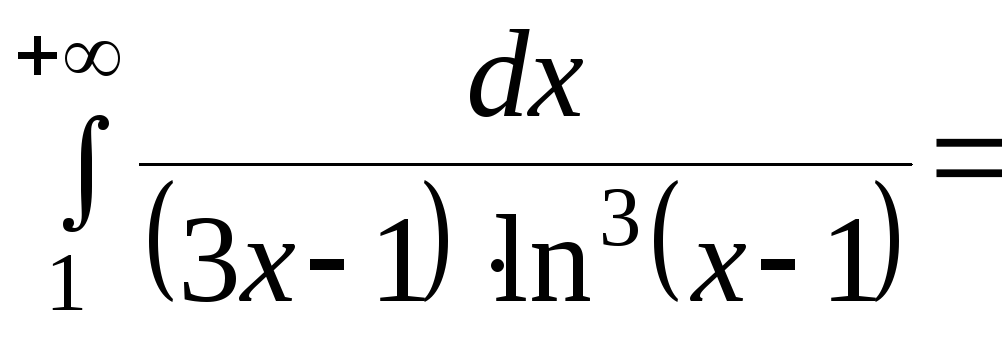



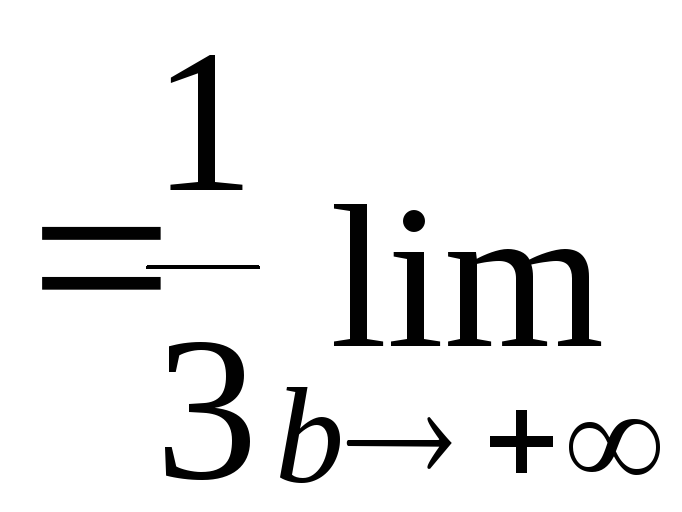
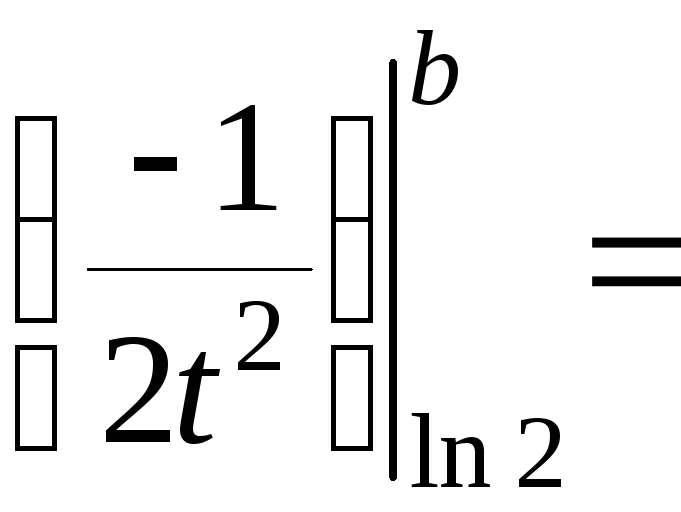

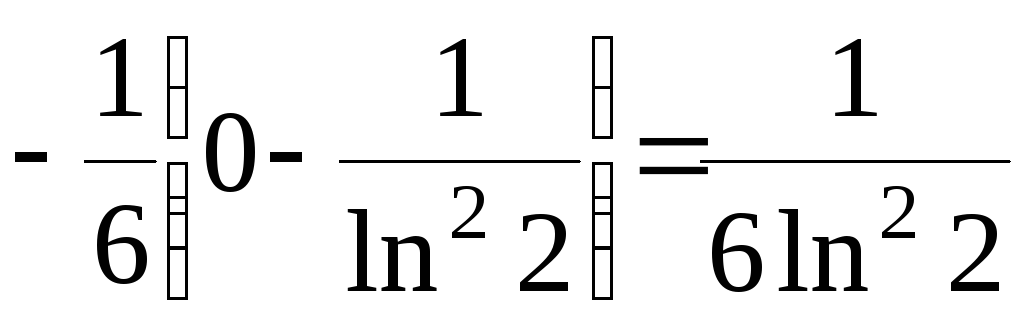 ― число.
― число.
Tак как несобственный интеграл сходится, то и исходный ряд сходится по интегральному признаку Коши.
Ответ: сходится.
б)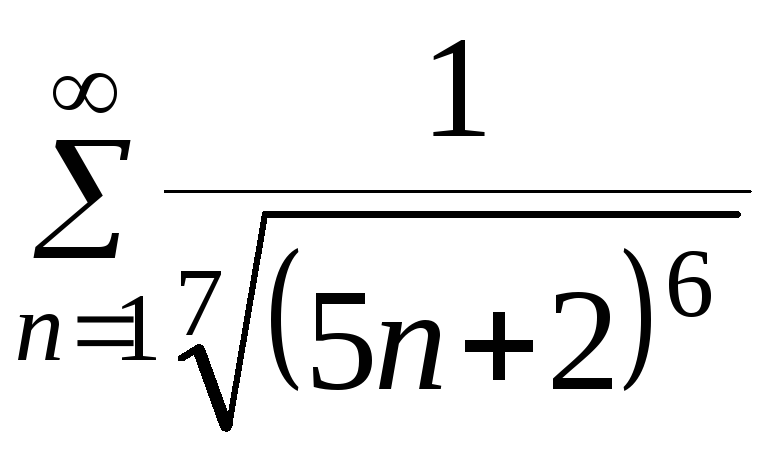 .
.
Решение.
Положим
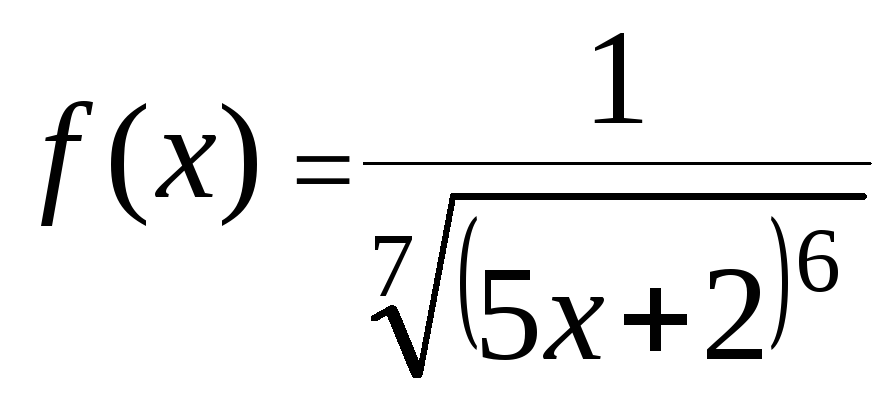 .
Эта функция удовлетворяет всем
требованиям интегрального признака
Коши.
.
Эта функция удовлетворяет всем
требованиям интегрального признака
Коши.
Рассмотрим несобственный интеграл
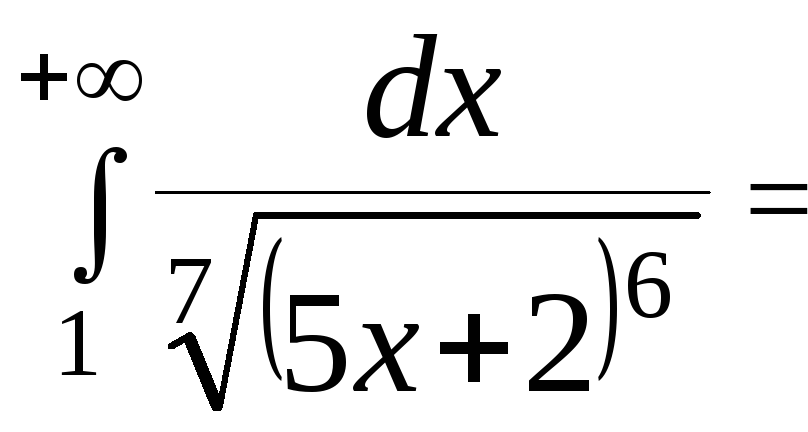
![]()
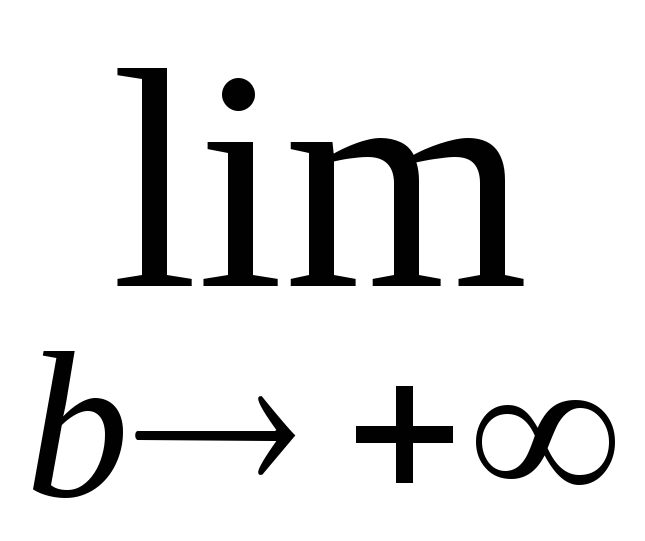
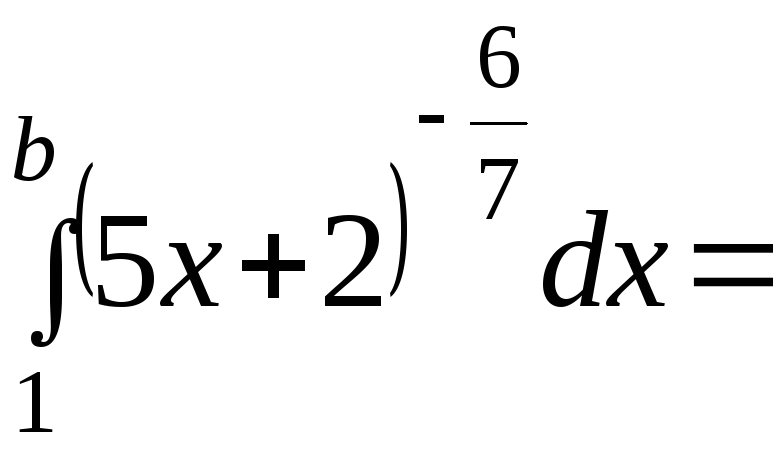

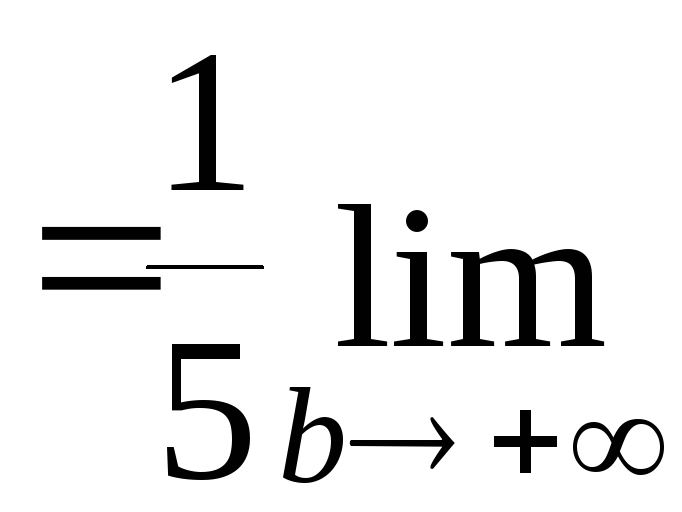
![]()
![]() .
.
Следовательно, несобственный интеграл расходится, тогда и ряд
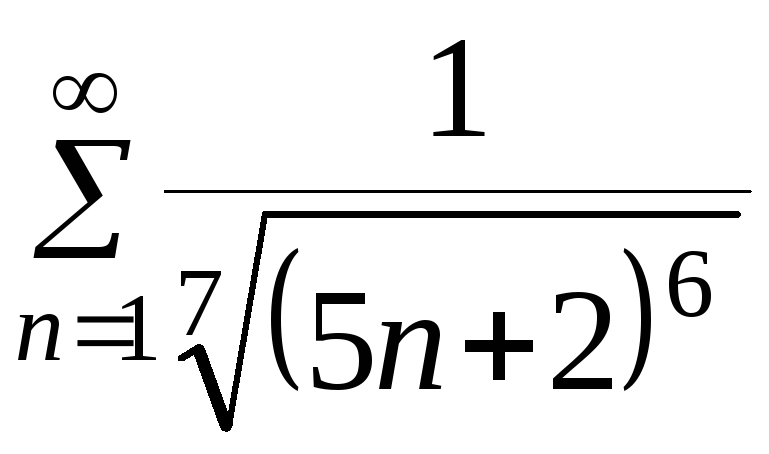 расходится по
интегральному признаку Коши.
расходится по
интегральному признаку Коши.
Ответ: расходится.
ЗНАКОЧЕРЕДУЮЩИЕСЯ ЧИСЛОВЫЕ РЯДЫ
Ряд
вида
![]() ,
где
,
где
![]() ,
называется знакочередующимся рядом.
Для знакочередующегося ряда справедлива
теорема Лейбница.
,
называется знакочередующимся рядом.
Для знакочередующегося ряда справедлива
теорема Лейбница.
Теорема Лейбница
Если
для знакочередующегося ряда
![]() выполняется 1)
выполняется 1)
![]() ;
2)
;
2)
 ,
то ряд сходится и его сумма S
удовлетворяет условию
,
то ряд сходится и его сумма S
удовлетворяет условию
![]() .
.
Наряду
со знакочередующимся рядом
![]() рассмотрим ряд из абсолютных величин
рассмотрим ряд из абсолютных величин
![]() ,
члены которого – положительные числа.
Если ряд из абсолютных величин
,
члены которого – положительные числа.
Если ряд из абсолютных величин
![]() сходится, то знакочередующийся ряд
сходится, то знакочередующийся ряд
![]() тоже сходится и
тоже сходится и
![]() называется абсолютно сходящимся. Если
ряд из абсолютных величин
называется абсолютно сходящимся. Если
ряд из абсолютных величин
![]() расходится, а знакочередующийся ряд
расходится, а знакочередующийся ряд
![]() сходится (по теореме Лейбница), то
сходится (по теореме Лейбница), то
![]() называется условно сходящимся.
называется условно сходящимся.
Исследовать
знакочередующиеся ряды
![]() на абсолютную и условную сходимость
можно по следующей схеме:
на абсолютную и условную сходимость
можно по следующей схеме:
1.
Вычислить .
Если
.
Если
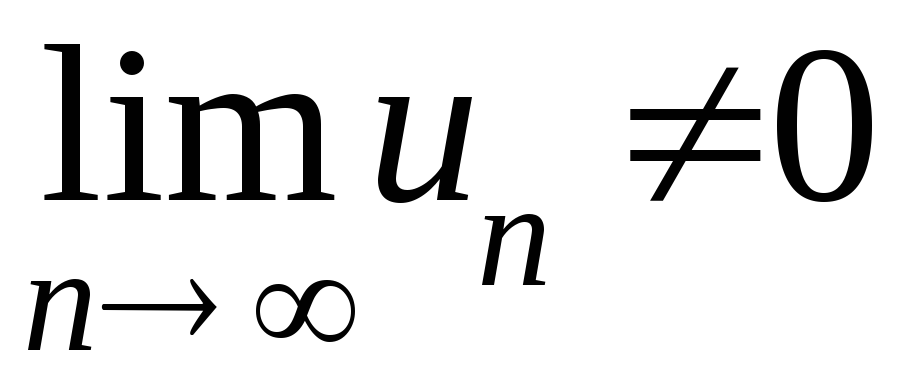 ,
то ряд расходится по достаточному
признаку расходимости и исследование
этого ряда закончено.
,
то ряд расходится по достаточному
признаку расходимости и исследование
этого ряда закончено.
2.
Составить ряд из модулей
![]() ― знакоположительный числовой ряд.
Используя признаки сходимости рядов с
положительными членами, исследовать
его на сходимость. Если ряд из модулей
― знакоположительный числовой ряд.
Используя признаки сходимости рядов с
положительными членами, исследовать
его на сходимость. Если ряд из модулей
![]() сходится, то исходный знакочередующийся
ряд
сходится, то исходный знакочередующийся
ряд
![]() сходится абсолютно и исследование этого
ряда закончено.
сходится абсолютно и исследование этого
ряда закончено.
3.
Проверить выполнение условий теоремы
Лейбница для знакочередующихся рядов.
Если условия выполнены, то знакочередующийся
ряд
![]() сходится условно, если нет – то расходится.
сходится условно, если нет – то расходится.
Пример 8. Исследовать знакочередующиеся ряды на абсолютную и условную сходимость.
а)
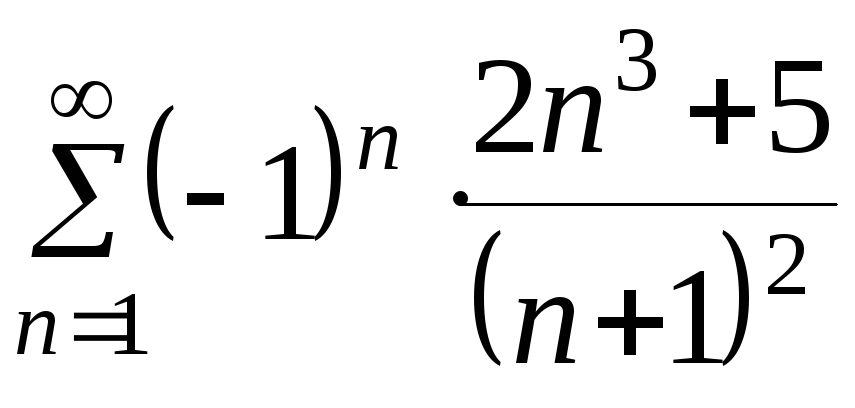 .
.
Решение.
Общий
член ряда
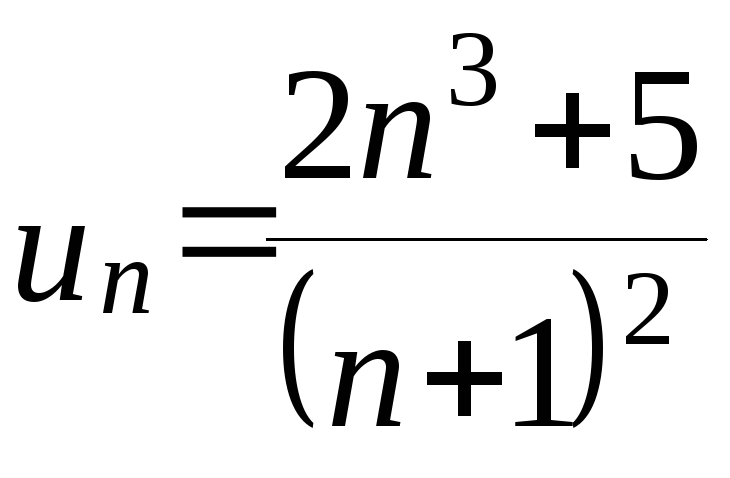 .
.
1.
Проверим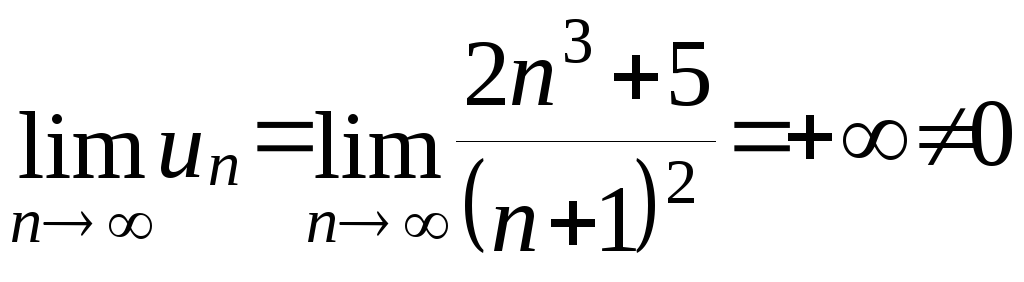 .
Следовательно, исходный ряд расходится
по достаточному признаку расходимости.
.
Следовательно, исходный ряд расходится
по достаточному признаку расходимости.
Ответ: расходится.
б)
 .
.
Решение.
Общий член ряда
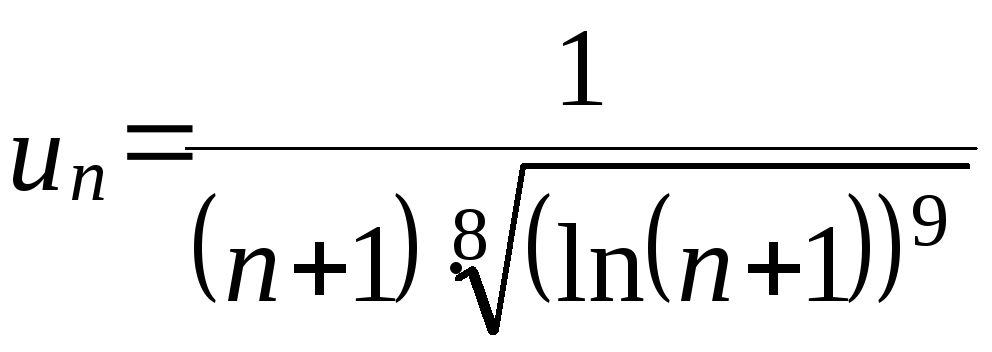 .
.
1.
Проверим
 .
.
2.
Составим ряд из модулей
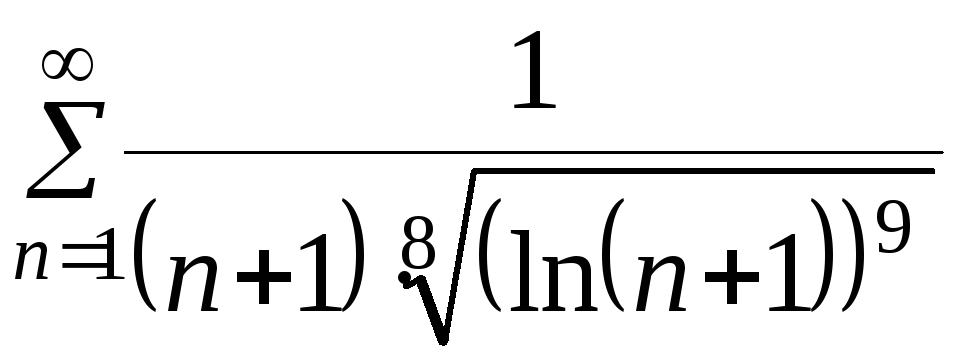 ― знакоположительный числовой ряд, и
применим к нему интегральный признак
Коши. Положим
― знакоположительный числовой ряд, и
применим к нему интегральный признак
Коши. Положим
 .
Эта функция удовлетворяет требованиям
интегрального признака Коши. Рассмотрим
несобственный интеграл
.
Эта функция удовлетворяет требованиям
интегрального признака Коши. Рассмотрим
несобственный интеграл

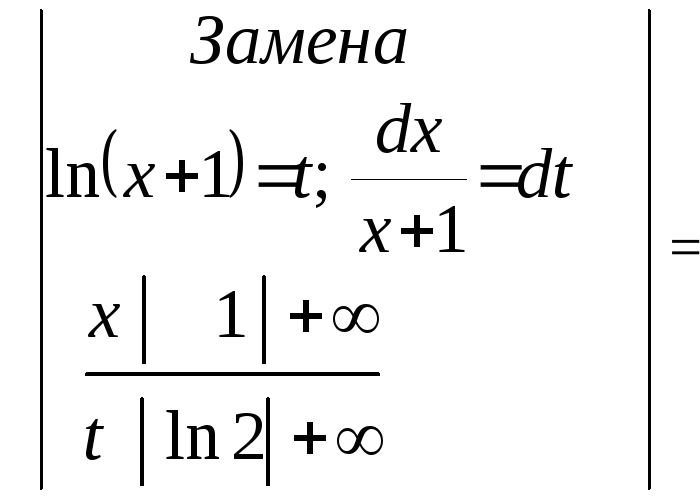

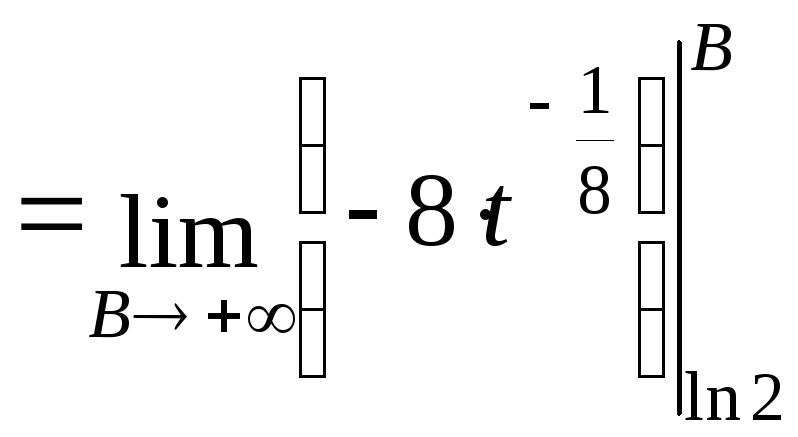 =
=
=
 число.
число.
Следовательно, несобственный интеграл и ряд из модулей сходятся одновременно по интегральному признаку Коши. Поэтому исходный знакочередующийся ряд сходится абсолютно.
Ответ:
сходится абсолютно.
![]()
в)
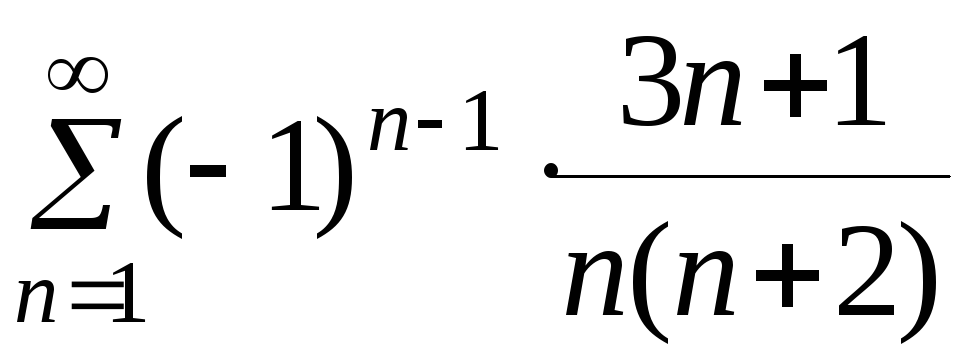 .
.
Решение.
Общий член ряда
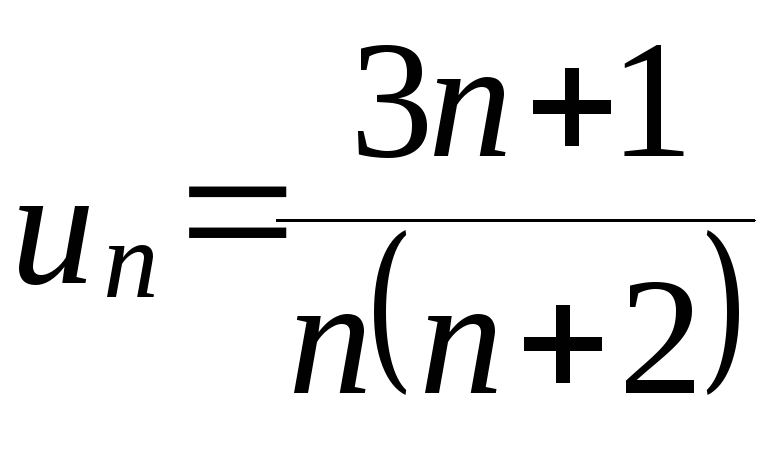 .
.
1.
Проверим
![]()
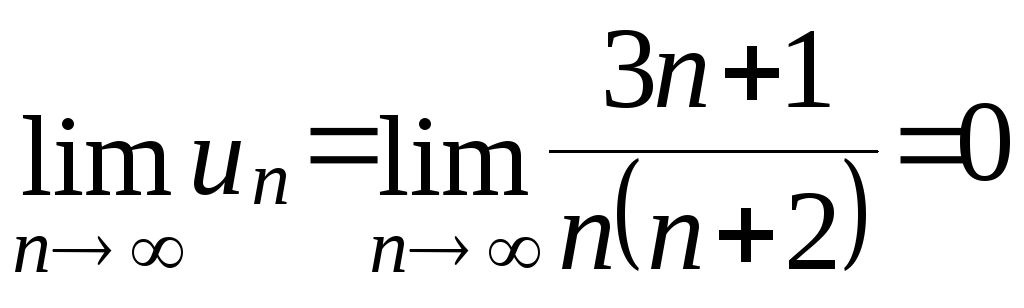 .
.
2.
Составим ряд из модулей,
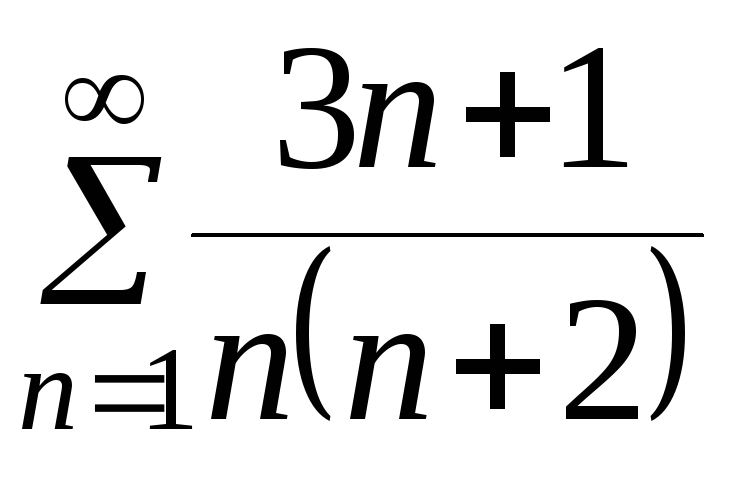 ― знакоположительный ряд, и применим
к нему второй признак сравнения. Для
сравнения возьмём расходящийся обобщённый
гармонический ряд
― знакоположительный ряд, и применим
к нему второй признак сравнения. Для
сравнения возьмём расходящийся обобщённый
гармонический ряд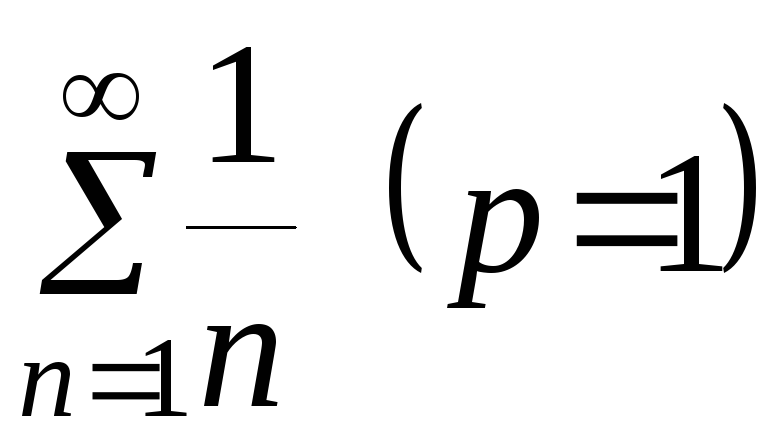 с общим членом
с общим членом
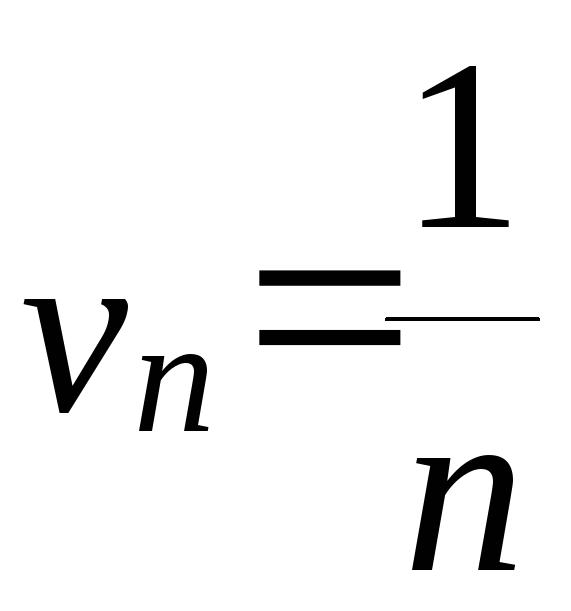 .
.
