4.1.3 Циклы паротурбинных установок

43. Рассчитать цикл Карно, который осуществляется насыщенным водяным паром. Установка работает по схеме рис. 28: сухой насыщенный пар при давлении p₁ = 2 МПа поступает в цилиндр паровой машины, где изоэнтропно расширяется до 0,1 МПа, после чего поступает в теплообменник; там влажный пар частично конденсируется до тех пор, пока его энтропия не становится равной энтропии жидкости в состоянии насыщения при р₂ = 2 МПа. Пароводяная смесь изоэнтропно сжимается компрессором до p₄ = p₁ и кипящая вода подается в котел, где она превращается снова в сухой насыщенный пар.

Определить параметры во всех точках цикла, термический КПД цикла, полезную работу, теплоту q₁, подведенную в цикле, и q₂, отведенную к нижнему источнику.

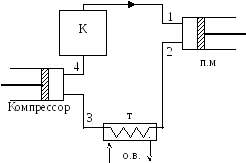
Рис. 28. Схема и цикл паровой машины

44. В установке, описанной в задаче 43, теплообменник Т (рис. 29) заменен конденсатором, в котором отработанный в цилиндре паровой машины пар полностью конденсируется до состояния 5, после чего конденсат сжимается поставленным взамен компрессора водяным насосом до давления р₄ и подается в котел, где подогревается до температуры насыщения, а затем превращается в сухой насыщенный пар. Иными словами, цикл Карно заменяется на цикл Ренкина. Каков термический КПД этого цикла; насколько он уменьшился по отношению к ? Начальное и конечное давление теже, что и в цикле задачи 43.

45. Паротурбинная установка работает по циклу Ренкина при следующих параметрах пара: перед турбиной р₁ = 9 МПа и t₁ = 535°С, давление в конденсаторе р₂ = 40 кПа (рис. 29). Определить работу турбины и питательного насоса, а также термический КПД цикла с учетом и без учета работы насоса и относительную разность этих КПД.

Рис. 29. Паротурбинная установка, работающая по циклу Ренкина

46. Паротурбинная установка работает по циклу Ренкина с начальными параметрами p₁ = 10 МПа и t₁ = 530°С. Давление в конденсаторе p₂ = 40 кПа. Определить термический КПД цикла Ренкина и сравните его с термическим КПД цикла Карно в том же интервале температур.

47. При одинаковой начальной температуре t₁ = 500°С построить кривую зависимости цикла паротурбинной установки отначального давления p_1, приняв его равным 5,0; 10,0; 15,0 и 20,0 МПа. Давление в конденсаторе одинаково, р_г = 40 кПа. Учесть работу питательного насоса. Представить циклы в Т,s − диаграмме.

48. При одинаковом начальном давлении р₁ =10 МПа построить кривую зависимости цикла паротурбинной установки от начальной температуры t₁, приняв ее равной 450, 500, 550 и 600°С. Давление в конденсаторе одинаково, р₂ = 50 кПа. Учесть работу питательного насоса. Представить

циклы в T,s − диаграмме.

49. Паротурбинная установка работает при параметрах пара перед турбиной р₁ = 9 МПа и t₁ = 535°С. Построить кривую зависимости термического КПД цикла от давления в конденсаторе р₂, которое принять равным 20, 40, 60, 80 кПа.

50. Определить зависимость термического КПД паротурбинной установки от начальных параметров пара, если при начальных и конечных давлениях соответственно р₁ = 3,0 МПа и р₂ = 40 кПа, пар перед турбиной:

1) имеет сухость x = 0,9; 2) сухой насыщенный; 3) перегретый до температуры 450°С.

51. Определить состояние пара за турбиной и подсчитать внутренний КПД (рис.30) паротурбинной установки, если начальные параметры р₁ = 13 МПа и t₁ = 565°С, давление в конденсаторе p₂ = 40 кПа, внутренние относительные КПД турбины и питательного насоса соответственно 0,85 и 0,87.

52. Определить внутренний относительный КПД турбины, если внутренние потери вследствие необратимости процесса расширения пара в турбине 138 кДж/кг. Состояние пара перед турбиной р₁ = 10 МПа, t₁ = 500°С, давление в конденсаторе р₂ = 40 кПа.

Рис. 30. Цикл паротурбинной установки в T,s − и h,s − диаграммах

53. Определить параметры пара перед конденсатором, где давление p₂ = 40 кПа, если параметры пара перед турбиной р₁ = 9 МПа и t₁ = 510°С, а внутренний относительный КПД турбины 0,87. Построить процесс в h,s − и Т,s −диаграммах. Задачу решать, пользуясь таблицами.

54. Определить параметры, определяющие состояние пара за турбиной и подсчитать внутренний КПД установки, если p₁ = 11 МПа, t₁ = 550°С, р₂= 40 кПа и внутренний относительный КПД турбины 0,85. Работу насоса не учитывать. Задачу решать, пользуясь h,s − диаграммой.

55. Сравнить внутренние КПД двух паротурбинных установок с атомными реакторами. Обе установки работают по двухконтурной схеме (рис. 31). В первом контуре (атомного реактора) теплоносителем является вода. В установке, выполненной по первому варианту, вода из первого контура направляется в парогенератор, во втором контуре которого образуется сухой насыщенный пар с давлением р₁ = 4 МПа. Этот пар и подается в турбину. В установке по второму варианту в парогенераторе образуется перегретый пар с параметрами р₁ = 1,6 МПа и t₁ = 250°С. Давление в конденсаторе р₂ одинаково для обеих установок и равно 40 кПа, а внутренний относительный КПД турбин 0,80. Циклы, по которым работают установки, изображены на рис. 31.

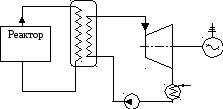
Рис. 31. Схема и цикл паротурбинной установки

56. К соплам паровой турбины поступает пар с параметрами р₁ = 17 МПа и t₁ = 550°С. После изоэнтропного расширения до t_b = 350°С он направляется в промежуточный пароперегреватель, где его температура повышается до t_a = 520°С. Затем пар расширяется в последующих ступенях турбины до давления в конденсаторе р₂ = 40 кПа (рис. 32).

Определить: 1) термический КПД цикла со вторичным перегревом; 2) насколько уменьшается влажность пара на выходе из турбины и насколько увеличивается термический КПД цикла в результате введения вторичного перегрева; 3) каковы средние интегральные температуры подвода теплоты в циклах с промежуточным перегревом и без него? Учесть работу насоса.

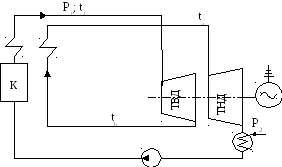
Рис. 32. Схема и цикл паротурбинной установки к задаче 56

57. В паровую турбину (рис. 33) поступает пар с параметрами р₁ = 9,0 МПа и t₁ = 540°С. Турбина имеет два регенеративных отбора в подогреватели поверхностного типа с каскадным сбросом конденсата греющего пара. Давление отборов р₁^◦ = 0,6 МПа и p₂^◦= 0,12 МПа. Давление в конденсаторе р_к = 40 кПа.

Определить термический КПД регенеративного цикла и удельный расход пара на 1 МДж и на 1 кВт∙ч выработанной энергии. Сравнить эти показатели с такими же показателями для цикла без регенерации. Вычислить величину экономии от введения регенеративного подогрева. Во всех задачах на регенеративные циклы считается, что в подогревателях вода нагревается до температуры конденсата греющего пара. Работа насосов не учитывается.

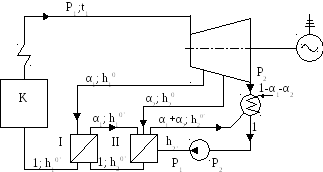
Рис. 33. Схема паротурбинной установки к задаче 57

58. В установке, описанной в задаче 57, поверхностные подогреватели заменены на смешивающие. Определить термический КПД регенеративного цикла, экономию за счет введения регенеративного подогрева и. часовой расход топлива, если мощность турбины N = 50 МВт, КПД парогенератора 0,90, теплота сгорания топлива Q^p_н = 28 МДж/кг, остальные условия те же, что и в задаче 57.

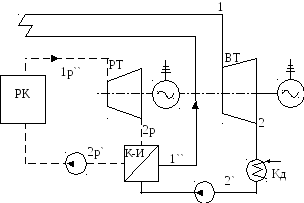
59. Бинарная ртутно − водяная установка работает по схеме, показанной на рис. 34. Ртутный котел вырабатывает сухой насыщенный пар при температуре t_1p’= 500°С, который направляется в ртутную турбину. Отработанный пар с температурой t_2p = 230°С идет в конденсатор − испаритель, где отдает теплоту конденсации воде, подаваемой насосом из конденсатора пароводяной турбины. При этом вода превращается также в сухой насыщенный пар, который перегревается в пароперегревателе, установленном в газоходах ртутного котла, и направляется в пароводяную турбину. Параметры водяного пара: р₁ = 2,4 МПа, t₁ = 520°С; давление в конденсаторе р₂ = 40 кПа.

Определить термический КПД бинарного цикла (рис. 34) и его отношение к термическому КПД цикла Карно, осуществляемого в тех же пределах максимальной и минимальной температур.

T

1

1p`

1p``

2p`

2p

m кг

Hg

1`

1’’

1 кг

H₂O

2`

2

S

Рис. 34. Схема и цикл бинарной ртутно-водяной установки

60. Парогазовая установка работает по следующей схеме (рис. 35): воздух из атмосферы (состояние 1) сжимается компрессором (состояние 2) и подается в топочное устройство высоконапорного парогенератора ВПГ, где сгорает топливо. Продукты сгорания сначала отдают часть своей теплоты нагретой до температуры кипения воде и водяному пару, циркулирующим в особом контуре, а затем направляются в газовую турбину ГТ (состояние 3), в которой, изоэнтропно расширяясь, совершают полезную работу. Отработавшие газы (состояние 4) идут в газовый подогреватель ГП и нагревают в нем конденсат водяного пара до температуры кипения (состояние 9), после чего выбрасываются в атмосферу (состояние 1). Кипящая вода из подогревателя ГП направляется в парогенератор ВПГ, где испаряется и перегревается (состояние 5). Перегретый пар, отработав в турбине высокого давления ТВД (состояние 6)_, снова перегревается за счет теплоты топочных газов ВПГ (состояние 7), затем работает в турбине низкого давления ТНД (состояние 8) и конденсируется в конденсаторе Кр. Водяной цикл, таким образом, замыкается. Идеальный бинарный цикл этой установки изображен на рис. 36.

Рассчитать термический КПД идеального бинарного парогазового цикла, если известны следующие параметры. Газ: р₁ = 0,1 МПа; t₁ = 20°С; t₃ = 800°С; t’₁ = 120^оС; =р₂/р₁= 8. Вода и водяной пар: р₅ = 1,3 МПа; t₅ = 565^оС; р₆ = p₇ = 3,0 МПа; t₇ = 565°С; p₈ = 30 кПа.

Найти отношение этого КПД и КПД цикла Карно для максимальной и минимальной температур бинарного цикла. Газ считать обладающим свойствами воздуха, теплоемкость газа с_Р считать постоянной. Работой водяных насосов пренебречь.

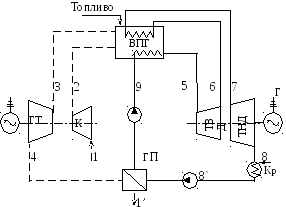
Г

Рис. 35. Схема парогазовой установки

Рис. 36. Идеальный бинарный цикл парогазовой установки

Рис. 37. Реальный бинарный цикл парогазовой установки

61. Парогазовая установка осуществлена по схеме рис. 35 с рабочими телами, имеющими те же параметры в основных точках цикла, что и в задаче 60.

Рассчитать внутренний КПД действительного цикла ПГУ (рис. 37), если дополнительно известны: внутренние относительные КПД компрессора и газовой турбины соответственно 0,85 и 0,87, внутренний относительный КПД пароводяных турбин 0,85. Известно также, что в газовом подогревателе ГП вода нагревается до t₁₀ = 300^оС, а газ охлаждается до t_1’ = 120°С.

62. В северных районах в холодное время года целесообразна работа бинарных паротурбинных установок, в которых нижний цикл осуществляется насыщенным паром низкокипящего вещества.

Определить термический КПД бинарного цикла вода — фреон-12. Схема установки и цикл изображены на рис. 38. Исходные данные для воды; р₁ = 16,0 МПа; t₁ = 540°С; p₂ = 0,12 МПа; для фреона-12: t’’_1ф = 95°С; t_2ф = 10°С. Сравнить полученный _бин с термическим КПД простого цикла Ренкина с рабочим веществом — водой, для которого максимальные параметры такие же, как и в бинарном цикле, а давление в конденсаторе р₂ = 40 кПа.

Дополнительные данные к прил. 2 для фреона-12 таковы:

при температуре насыщения t_S = 95°С энтальпии h' и h" соответственно равны 522,1 и 599,2 кДж/К, а энтропии s' и s" составляют 4,5020 и 4,7115 кДж/(кг∙К).

1'ф

Рис. 38. Схема и цикл бинарной паротурбинной установки

63. В паротурбинной установке вода и пар работают, осуществляя необратимый цикл, в котором состояние рабочего тела меняется в следующей последовательности (рис. 39): конденсат в состоянии 2' адиабатно сжимается насосом до состояния 3д и поступает в паровой

котел, в котором нагревается до кипения, испаряется и перегревается. Находясь в состоянии 1" пар направляется к турбине, попутно излучая часть своей энергии в окружающую среду и теряя давление из-за сопротивления трению. В состоянии 1' перед турбиной пар адиабатно дросселируется в регулировочном клапане до давления р₁. Далее пар так же адиабатно расширяется в турбине до давления р_{2 =} р_2д и в состояний 2д входит в конденсатор, где и конденсируется при помощи охлаждающей воды. Цикл, таким образом, замыкается точкой 2'. Известны следующие параметры: р"₁ = 12 МПа, t"₁ = 540°С; р’₁ = 11 МПа; t'₁ = 540°С; р₁ = 9 МПа; р₂ = 30 кПа. Коэффициент полезного действия: относительный внутренний турбины =0,85, насоса= 0,90, механический= 0,96, электрогенератора=0,97. Теплота сгорания топлива Q^р_н = 30 000 кДж/кг. Коэффициент полезного действия парового котла = 0,92. Составить для этой установки баланс энергии и найти КПД установки на клеммах электрогенератора.

Рис. 39. Паротурбинный цикл

64. Составить эксергетический баланс для установки, описанной в задаче 63, определив изменения эксергии в каждом из характерных узлов. Подсчитать эксергетические КПД тех же узлов и установки в целом. В качестве параметров окружающей среды принять параметры воды: T₀ =2 90 К и р₀ = 1000 кПа. Воспользоваться таблицей параметров к задаче 63.

65. Определить эксергетические потери в каждом из узлов установки, описанной в задаче 63. Найти для этих узлов и для всей установки коэффициенты эксергетических потерь, а также эффективный КПД установки. Использовать результаты решений задач 63 и 64.