Решение:
а)
из условия
тогда
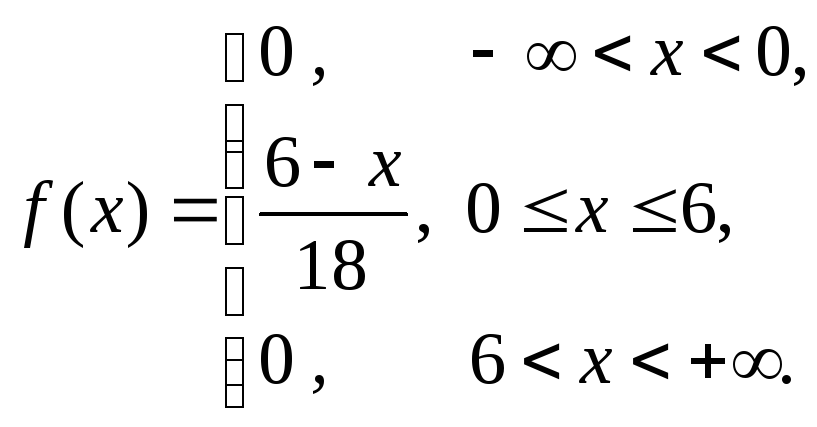
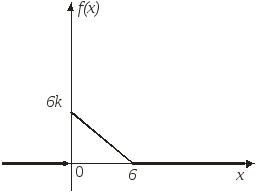
б)
При
построении
воспользуемся свойством
.
|
При
|
|
|
при
|
|
|
при
|
|
.
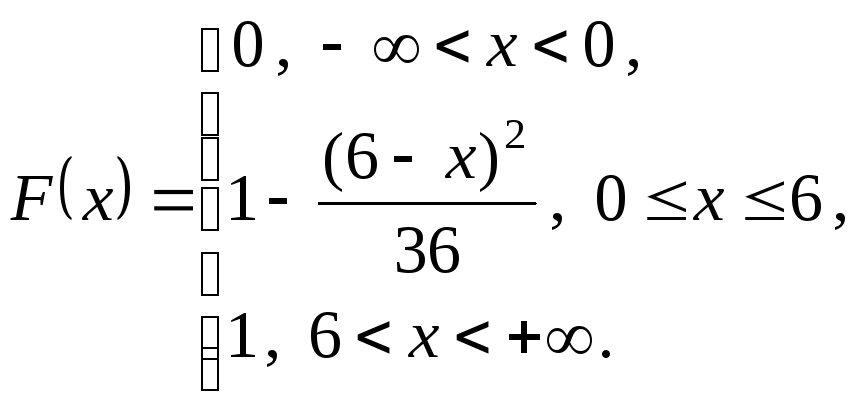
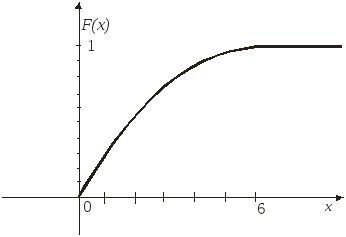
в)
.
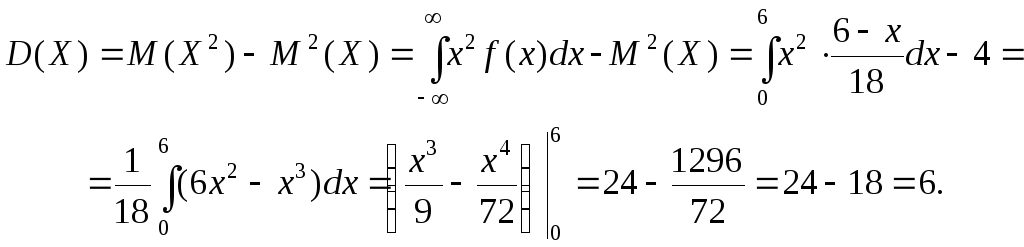
г)
.
9. На запуск двигателя тратится в среднем 2.5 попытки. Считая, что вероятность запуска в каждой попытке одинакова, найти вероятность запуска двигателя не более, чем за 3 попытки.
Здесь
имеет место геометрическое распределение
случайной величины Х
равной числу
попыток до запуска двигателя, причем
.
Тогда из
и
.
10.
Случайная величина Х
имеет биномиальное распределение
(распределение Бернулли) с математическим
ожиданием
и дисперсией
.
Найти вероятность события
.
Для
биномиального распределения
,
получим систему уравнений:
,
тогда
и
.
Искомую
вероятность
находим с помощью формулы Бернулли.
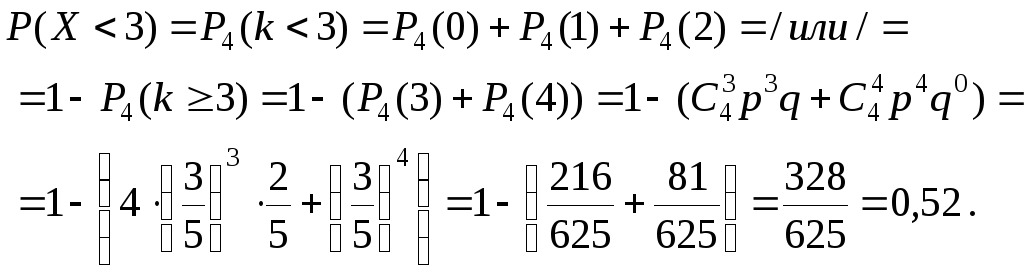
11.
Для случайной величины Х,
имеющей распределение Пуассона
вероятность события
равна 0.4. Найти вероятность события
.
Из
формулы
для
,
Тогда
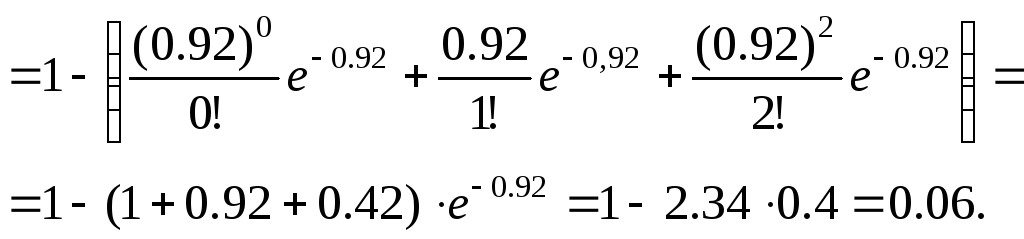
12.
Случайная величина Х
имеет равномерное распределение в
интервале
,
причем
и
.
Найти вероятность события
.
Для
равномерного распределения
,
.
По
условию
.
Для
и
интегральная функция имеет вид:
13.
Случайная величина Х
имеет показательное распределение и
при этом численно
.
Найти вероятность события
.
Из
формул
,
или
.
Тогда
и интегральная функция будет:
14.
Методами математической статистики
установлено, что для данного региона
роста призывников в ряды вооруженных
сил имеют нормальное распределение с
параметрами
.
Найти ожидаемое число призывников 3-го
роста из 1000 человек.
Отметим, что третий рост соответствует интервалу (167, 173).
По
формуле
получим
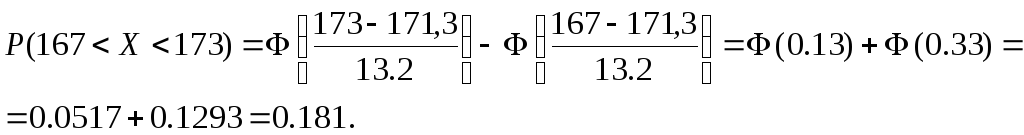
Тогда ожидаемое число призывников третьего роста
человек.
Примечание:
значения
и
взяты из таблицы значений функции
Лапласа
.
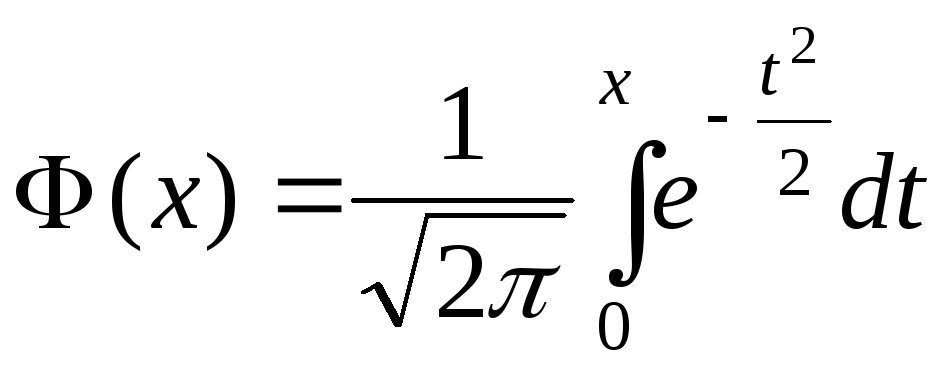ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Для получения своих личных данных надо подставить α и β в задания и посчитать соответствующие им выражения.
α – предпоследняя, а β – последняя цифра шифра студента.
Например, если шифр студента 1004-206, то α=0, β=6.
1 Из урны, в которой находятся (12-β) белых, (2+α) черных и 3 синих шара наудачу, без возвращения в урну извлекаются:
1) 5 шаров. Найти вероятность того, что среди этих шаров окажется ровно два белых.
2) 2 шара. Найти вероятность того что:
а) эти шары будут разного цвета;
б) эти шары будут одного цвета;
в) взятый из них наудачу один шар окажется белым.
3) 3 шара. Найти вероятность того, что:
а) эти шары будут разного цвета;
б) эти шары буду одного цвета;
в) среди этих шаров будет хотя бы один белый.
4) 2 шара, и они оказались разного цвета. Найти вероятность того, что это белый и черный шары.
2 В урне находятся (5+β) белых и (15-β) черных шаров. Наудачу, шар извлекается и возвращается в урну 3 раза. Найти вероятность того, что белый шар появится:
а) ровно 2 раза;
б) не менее одного раза.
3 В урне находятся (12-β) белых и (12-α) черных шаров. Наудачу извлекаются без возвращения в урну 3 шара. Построить ряд распределения и найти математическое ожидание случайной величины, равной числу белых шаров среди извлеченных трех шаров.
4 Дискретная случайная величина Х с математическим ожиданием М(Х)=6+0,1α-0,3β задана рядом распределения
|
xi |
α-10 |
0 |
10-β |
20 |
|
pi |
p1 |
0,4 |
p3 |
0,2 |
а) Найти р1 и р3;
б) построить многоугольник распределения;
в) построить интегральную функцию распределения F(x) и её график;
г) вычислить дисперсию D(x).
5 Плотность распределения непрерывной случайной величины X имеет вид
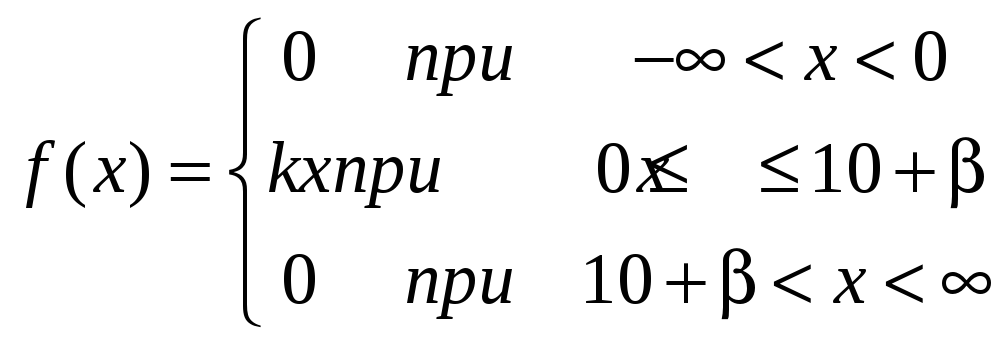
Найти: а) параметр k;
б) математическое ожидание М(х);
в) интегральную функцию распределения F(x) и её график;
г) вероятность события X >10-α.
6
Случайная величина имеет биноминальное
распределение с математическим ожиданием
M(x)=
и дисперсией D(x)=
.
Найти вероятность события X
2.
7
Случайная величина имеет нормальное
распределение с математическим ожиданием
M(x)=
и дисперсией D(x)=
.
Найти вероятность события X
>0.
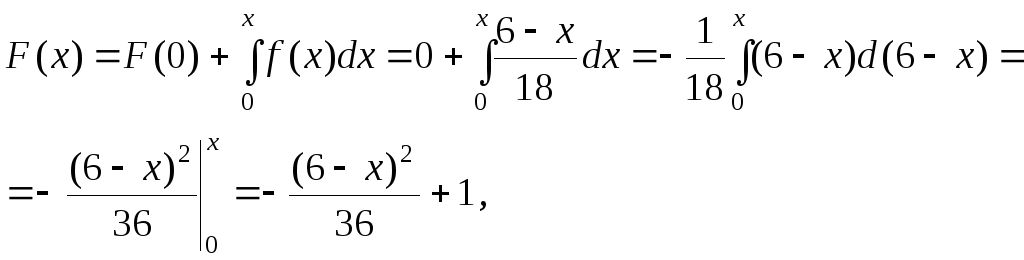
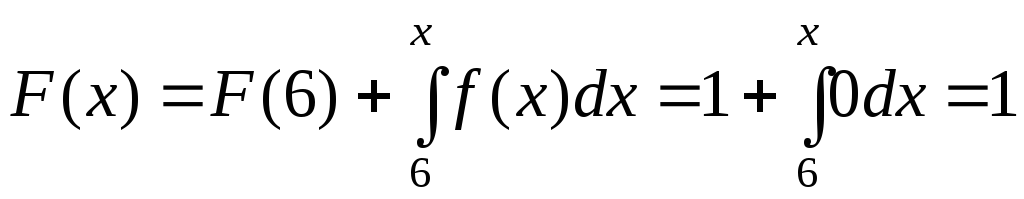