7.7. Резонанс в цепи с двумя параллельными ветвями

На рис. 7.12 а (показана схема параллельного соединения двух ветвей R₁, L и R₂, С. В такой схеме возможен резонанс токов. На рис. 7.12 б показана векторная диаграмма данной схемы в режиме резонанса токов. На диаграмме отмечено, что вектор общего тока совпадает по направлению с вектором приложенного напряжения, т. е. эти векторы совпадают по фазе, что и свойственно режиму резонанса. Входная комплексная проводимость

.

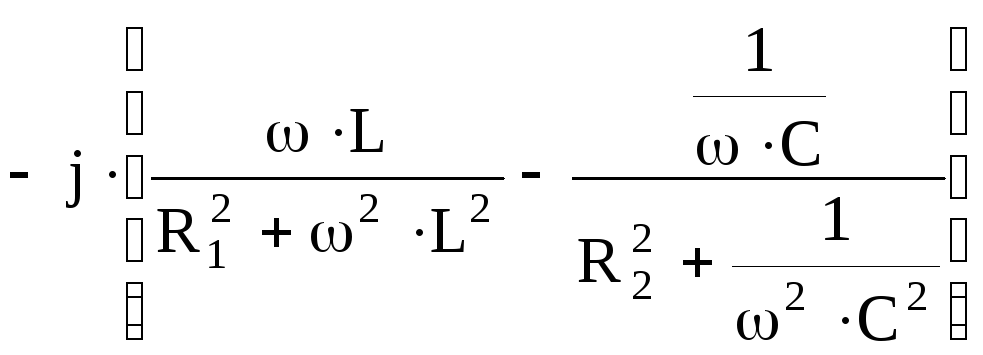При резонансе токов b = 0, т. е. .

Как видно из последней формулы, резонанс может быть достигнут изменением одной из величин ,L, С, R₁, R₂. Однако этот режим не всегда может быть получен, а именно, когда значение изменяемой величины (при заданных остальные четырех величинах) получается при решении последнего уравнения мнимым или комплексным. Для L и С могут быть получены и по два вещественных значения. В таком случае могут быть получены два резонансных режима.

Решая последнее уравнение относительно а, найдем следующее значение для резонансной частоты

Для получения вещественного значения необходимо, чтобы сопротивленияR₁ и R₂ были оба или меньше или оба больше, чем .

Если R₁ = R₂ = 0, то (идеальный контур).

Если , то резонанс будет иметь место при любой частоте, так как в этом случае получается неопределённость.

7.8. Резонансные кривые параллельного контура

Для идеального параллельного контура (когда R₁ = R₂ = 0) резонансная кривая показана на рис. 7.13. При этом и резонансная частота.

Входное сопротивление идеального параллельного контура при резонансе равно бесконечности, , поэтому при резонансной частоте общий ток равен нулю. Однако токи в ветвяхисуществуют, они одинаковые по модулю и противоположны по фазе (см. рис. 7.12б).

На рис. 7.14 приведена резонансная кривая реального контура. Эта кривая может быть рассчитала по формуле

А.

Пример 7.1. Для последовательного контура рис. 7.6 а найти: 1) резонансную частоту,

2) -значение тока при резонансе, 3) частоту , при которой будет ,

4) частоту , при которой будет , 5) значение , 6) значение ,

7) добротность контура - Q, 8) полосу пропускания .

Дано: R = 100 Ом, L = 0,2 Гн, C = 1 мкФ, U = 100 мВ.

Решение

Используем результаты § 7.3.

1. .

2. .

3. .

4. .

Находим максимальные значения напряжений на конденсаторе и катушке при частотах

и соответственно.

5.

В.

6.

В.

7. По определению добротность контура: .

8. Полосу пропускания найдем, если решим систему

После подстановки численных данных

Подставим это в предыдущее уравнение.

Откуда .

Получим .

Полоса пропускания

Пример 7.2. Для параллельного контура рис. 7.12 а дано:

R₁ = 100 Ом; R₂ = 200 Ом; L = 0,2 мГн; С = 1 мкФ; Е = 100 В.

Найти: 1) резонансную частоту; 2) реактивные сопротивления x_L и x_С;

3) токи в ветвях и общий ток при резонансной частоте.

Решение

В начале рассчитаем частоту резонанса по результатам

.

Реактивные сопротивления Ом;Ом

Полные сопротивления ветвей Ом;

Ом.

Токи ветвей А;

А.

Общий ток .

Реактивная составляющая общего тока при резонансе равна нулю.

Пример 7.3. Последовательно-параллельная схема рис. 7.15 находится в режиме резонанса напряжения. Известно, что входное сопротивление цепи на постоянном токе равно 200 Ом. Входное сопротивление цепи при резонансе равно 100 Ом.

1. Найти реактивные сопротивления х_L и х_C для резонансного режима.

2. Рассчитать комплексные значения всех токов при Е = 200 В.