Пособие по ТОЭ-2ч / Глава 13

Глава тринадцатая. КРУГОВЫЕ ДИАГРAMMЫ

13.1. Общие и методические замечания

При расчете сложных линейных электрических цепей воз­никает задача определения токов и напряжений в зависимо­сти от изменения одного из параметров цепи. Использование аналитических методов расчета цепей (законы Кирхгофа, методы контурных токов, узловых потенциалов, эквивалент­ного генератора и других) представляет трудоемкую задачу, ввиду того, что расчет необходимо проводить многократно при различных значениях изменяющегося параметра.

Графический метод расчета заключается в том, что ис­следуемые комплексные выражения представляются на комплексной плоскости векторами, геометрические места кон­цов которых изображаются различными кривыми; такие кри­вые называются годографами, они наглядно показывают изменения модулей и фаз электрических величин или их соотношении в зависимости от изменения того или иного параметра. Такие годографы могут иметь сложную форму. Переменными параметрами могут быть величина и фаза ЭДС или тока источника, частота , активное сопротивле­ние r , индуктивность L, взаимная индуктивность М, емкость С, а также реактивная составляющая сопротивления или проводимости любого элемента.

Простейшие диаграммы представляют собой прямые ли­нии или дуги окружностей, называются соответственно ли­нейными и круговыми диаграммами и имеют наибольшее практическое применение при исследовании линейных элект­рических цепей.

13.2. Круговые диаграммы для неразветвленной электрической цепи

Сложную линейную электрическую цепь относительно из­меняющегося сопротивления нагрузки , согласно методу активного двухполюсника (гл. 2, § 2.5) можно представить эквивалентным источником с напряжением на зажимах двух-

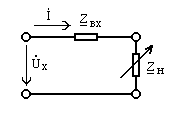
Рис. 13.1

полюсника в режиме холостого хода и входным сопротив­лением , (рис. 13.1).

Пусть с неизменным аргументом

, и модулем , изменяющимся от нуля до бесконечности, пусть . Построим

годограф вектора тока при изменении .

Ток в цепи равен

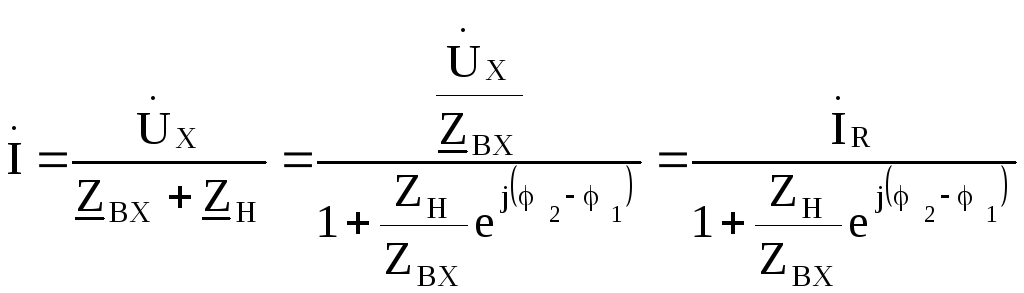
или

(13.1)

где ток короткого замыкания при =0. Урав­нение (13.1) .представляет уравнение окружности на комп-

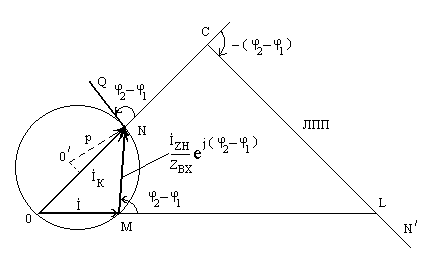
Рис. 13.2

лексной плоскости, а геометрическим местом конца вектора при изменении является дуга окружности.

Действительно, при любых значениях сумма двух изменяющихся векторов и

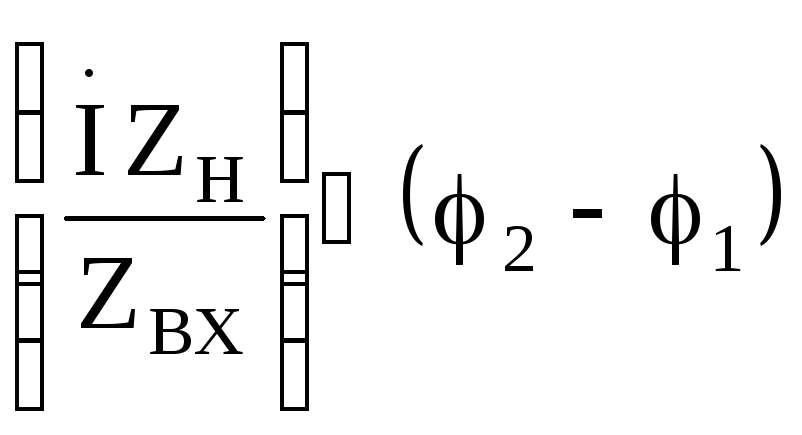pавна не­изменному (рис. 13.2). Имеем треугольник, одна сторона

которого вектор , другая-вектор , по­вернутый относительнона yroл ,

третья – =const. Таким образом, имеем треугольник с постоянным основанием постоянным

углом при вершине . Геометрическим местом вершин такого треугольника являет­ся

окружность, а геометрическое место концов вектора - дуга окружности OMN, для которой

вектор – xорда. Ес­ли вектор , скользя по дуге окружности OMN, совпадает с вектором

(рис. 13.2), то угол при вершине = const становится углом между касательной к

окружности NQ в точке N и продолжением вектора . Центр окружности определим

следующим образом. На комплексной плоскости откладываем вектор , под углом

к продолжению проводим прямую NQ, которая является касательной к окружности.

Восстановив перпендикуляр к середине хорды ON и перпендикуляр к касательной NQ в точке N,

найдём точку их пересечения О', которая является центром окружности. Радиус

окружности

Покажем, как найти вектор для любого значения изменяющегося параметра . По направлению вектора от­ложим из точки О отрезок ОС, равный в произвольном мас­штабе величине . Из точки С под углом – к вектору проведем прямую CN' до пересечения с продолже­нием ОМ. Треугольники OMN и OLC .подобны по двум уг­лам, поэтому

Таким образом, если отрезок ОС соответствует , то отрезок CL в том же масштабе соответствует изменяющейся величине . Линия СN^/ называется линией переменного пара-метра (ЛПП), на которой откладываются отрезки, соответствующие различным значениям .

В результате, построение диаграммы сводится к следующему:

1. Проводим вектор соответствующий хорде окружности.

2. Определяем центр окружности и радиусом ρ проводим ее.

3. Из точки О по направлению вектора в произвольном масштабе откладываем отрезок

ОС, соответствующий .

4. Под углом - к вектору из точки С прово­дим ЛПП CN', на которой в

масштабе величины откла­дываем отрезок CL, соответствующий .

5. Соединяем прямой точки О и L, точка пересечения этой прямой с окружностью определяет положение вектора на окружности при заданном.

Точка N соответствует =0, точка О – =, так как ЛПП параллельна касательной в точке О. Дуга OMN соответствует положительным значениям . Следует отметить, что дуга окружности, по которой перемещается точка М, расположена относительно хорды ON со стороны ЛПП.

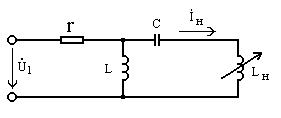
Рис. 13.3

Пример 13.1. В цепи рис. 13.3 . Индуктивность изменяется от нуля до бесконечности. Построить геометрическое место концов вектора при изменении .Определить, при каком сопротивлении ток максимален.

Решение

Рассматриваемая электрическая цепь относительно соп­ротивления нагрузки может быть заменена эквивалентной с параметрами и (рис. 13.1). Напряжение опреде­лим как напряжение на нагрузке при :

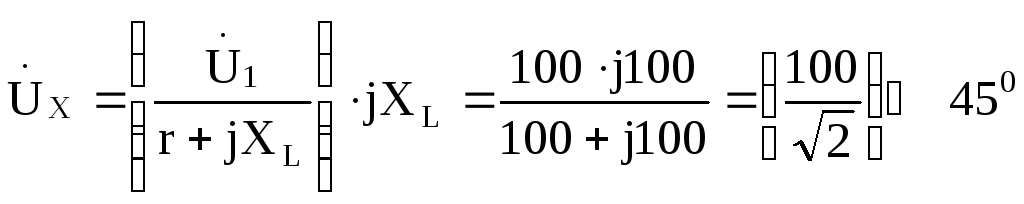
Conpотивление входное сопротивление относительно нагрузки

Ток короткого замыкания (при )

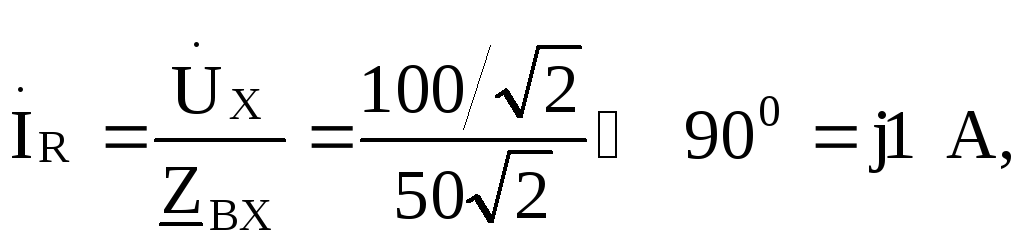
Таким образом, уравнение (13.1) для рассматриваемой за­дачи примет вид

Круговая диаграмма тока приведена на рис. 13.4 ( см. также рис. 7.18).

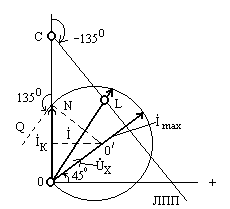
Рис. 13.4

1. Выбираем масштаб тока m₁ = 0,2 А/см и проводим век­тор , откладываем напряжение .

2. Определяем центр окружности; под углом 135⁰ к век­тору из точки N проводим прямую NQ,

восставим перендикуляр к середине хорды ON и перпендикуляр к NQ в точ­ке N, точка их

пересечения есть центр окружности. Радиус окружности

=0,707 А.

3. В направлении из точки О откладываем отрезок, со­ответствующий модулю

сопротивления Ом в произвольном масштабе; пусть m_R=10 Ом/см.

4. Из точки С под углом –135⁰ к проводим ЛПП, на которой в масштабе m_R = 10 Ом/см

откладываем отрезки, соответствующие изменяющемуся сопротивлению нагрузки

(при =30 Ом, точка L).

5. Точка пересечения прямой OL с окружностью определяет искомый ток, из диаграммы

имеем .

Максимальное значение тока наблюдается npи сов­падении и (режим резонанса

напряжения), поэто­му из диаграммы имеем

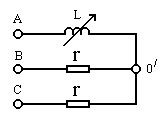
Рис. 13.5

Пример 13.2. В схеме фазоуказателя (рис. 13.5) трехфаз­ный источник симметричный, соединенный звездой U_Ф=220 В, нагрузки в фазах r = 150 Oм = const, L изменяется от нуля до бесконечности. Построить годограф напряжения смещения нейтрали и определить напряжения на фазах нагрузки.

Решение

Напряжение относительно изменяющегося сопротивления равно

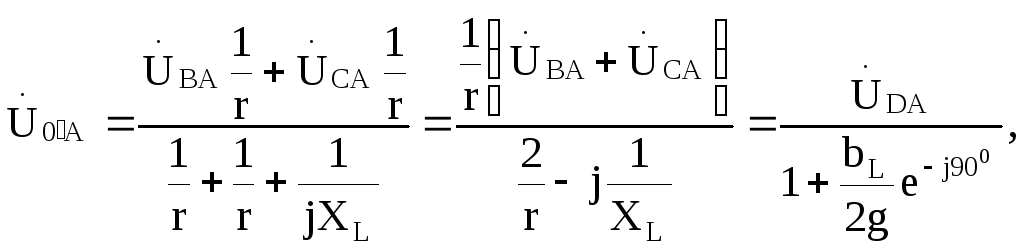(13.2)

где – реактивная и активная проводимо­сти, причем g = const, b_L -изменяющаяся

величина, -линейные

напряжения. Уравнение (13.2) соответствует уравнению (13.1), поэтому годографописывает

круговую диаграмму (рис. 13.6).

Рис. 13.6

Вектор , имеет начало в точке А, конец в D,

причем точка D, лежит на середине линейного напряжения . Отрезок AD является хордой.

Из точки A в направлении AD в масштабе m,от­кладываем проводимость

.(AN).Из точки N под углом -(-90°) = 90° по отношению к вектору про­

водим линию переменного параметра, на которой в том же масштабе m_g откладываем реактивную

проводимость . Центром окружности является середина хорды DA, которая является

диаметром. Из диаграммы следует что точка A соответствует режиму , точка

D- . Напряжения и на нагрузках в фа­зах В и С различны, причем

ВО' меньше СО', следовательно, если вместо резисторов r включить одинаковые лампы нака­

ливания, то яркость их будет различной, причем в фазе С ярче, чем в фазе В. Поэтому можно

сделать вывод что та лампа, которая горит ярче, включена в фазу С.

Задачи для самостоятельного решения (к главе 13)

1. В электрической цепи (рис. 13.3) индуктивное сопротивление нагрузки 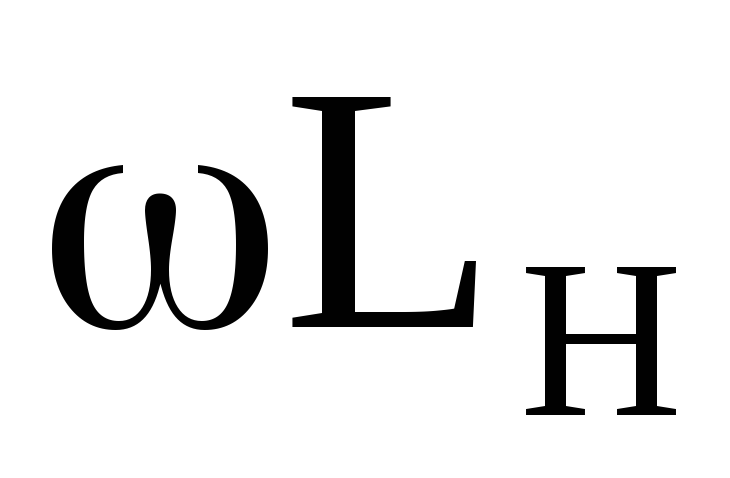заменено

активным conpотивлением r_н. Построить годограф вектора тока при изменении r_н от нуля до

бесконечности. По диаграмме найти при r_н = 50 0м.

Ответ: .

2. В схеме рис. 13.5 катушка индуктивности заменена кон­денсатором, величина емкости

которого изменяется от нуля до бесконечности. Построить годограф изменения потенциа­ла и найти напряжения на фазах приемника.

Ответ: .

ЛИТЕРАТУРА

1. Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники.Т.1.Л. Энергоатомиздат, 1981.534с.,

2. Основы теории цепей. Г. В. Зевеке, П. А.Ионкин, А. В. Нетушил, С. В. Страхов.

М.: Энергия, 1975. 752 с.

3. Теоретические основы электротехники/Под ред. П. Л. Ионкина. М.; Высшая школа, 1976.

Т. 1. 383 с.

4. Бессонов Л. А. Теоретические основы электротехники. М.: Высшая школа, 1978. 231 с.