9.3. Расчет трехфазных цепей с симметричной нагрузкой

Исходными данными являются:

— схема трехфазной цепи,

— фазные ЭДС генератора,

— сопротивления фаз нагрузки.

Искомыми величинами являются токи.

Рис. 9.9

1. Обмотки генератора и сопротивления нагрузки соединены в звездy, как показано нaрис. 9.9

(без нулевого провода).

По условию:

Заданные фазные ЭДС генератора в комплексной форме можно записать так

если , то

,

Напряжение между нейтральными точками нагрузки и генератора находим по методу двух узлов

Так как для симметричной нагрузки и, то, учитывая

соотношение (9.2),найдем

Вывод , который необходимо запомнить: у симметричной нагрузки, соединенной звездой,

потенциал нейтральной точ­ки равен потенциалу нейтральной точки генератора. Отсюда

следует, что эти точки можно соединить между со­бой проводником и тогда становится ясным,

что =,=,=и токи в фазах нагрузки будут

Из схемы очевидно, что фазный ток нагрузки является ли­нейным током и он же есть ток в фазе

генератора.

Покажем, что напряжение между любыми двумя линейными проводами, называемое -

линейным напряжением, в раз больше фазного напряжения, т. е..

Для этого найдем, например, разность комплексных по­тенциалов точек А и В

Таким образом, линейное напряжение в раз больше фазного и на 30°

опережает его. Аналогично можно

Рис. 9.10

получить, что линейное напряжение опережает фазное напряжениена 30°и враз больше его и линейное напряжениеопережает фазное напряжение на 30°

uвраз больше, его. Приведенные соотношения проще всего запомнить с помощью построения топографической диаграммы для фазных и линейных напряжений, приведен­ной на рис. 9.10.Векторы фазных напряжений,, и этой диаграммы относятся ках к фазным напряжениям ге­нератора, так и к фазным напряжениям нагрузки, т. е. топо­графические диаграммы фазных напряжений генератора и нагрузки совпадают. Векторная диаграмма токов для схемы рис. 9.9показана на рис. 9.10пунктирными линиями.

Следует отметить, что расчет токов и напряжений на от­дельных участках трехфазной цепи с симметричной нагруз­кой можно и нужно проводить на одну фазу, например, на фазу А, тогда соответствующие величины в фазе Вбудут отличаться только аргументом (углом) величиной

-120°,а в фазеС.– аргументом величиной +120°.

Пример 9.1.В цепи рис. 9.11. рассчитать токи и построить векторно-топографическую диаграмму приr==10 Ом и фазном напряжении генератора =220В.

Рис. 9.11

Решение

Так как точки 0и 0'имеют одинаковые потенциалы, то для фазы А=.

Принимаем

==220В, тог­да .

Токи в фа­зах ВиСотличаются от токатолько своими аргумента­ми, т.е.

Рис. 9.12

Построение векторно-топографической диаграммы прове­дем в следующей последовательности. Отложим по действительной оси вектор фазного напряжения фазы А генератора .

Затем в выбранном масштабе для напряжения под углами —120°и +120°по отношению к этому вектору из точки 0,потенциал которой принят равным нулю, отложим соответственно векторы

и, как показано на рис. 9.I 2.Далее под углом —45°по отношению к вектору

откладываем в маштабе для тока вектор токаВекторы токовистроим

соответственно, под углами —120°и+120°по отношению к вектору тока. Затем для каждой

из фаз нагрузки определяем комплексные потенциалы точек 1, 2 и 3 по отношеную к потенциалу

точки 0',равному так-же нулю:

Найденные комплексные потенциалы откладываем от точки О' по направлениям соответствующих токов в масштабе для напряжения.

Далее определяем потенциалы точек А, В, Спо отноше­нию к потенциалу точки О':

Отметим, что напряжения на индуктивностях нагрузки можно было бы найти графически,

используя соотношения:

;;

При этом для получения .напряжения надо на диаграм­ме соединить точкиАи 1прямой и указать направление этой прямой к первому индексу, т.е. к точкеА.Аналогично . получают напряжения;

2.Обмотки генератора и сопротивления нагрузки соеди­нены в треугольник, как показано на рис. 9.13.

Из схемы рис .9.13непосредственно следует, что фазные напряжения генератора, именуемые теперь как,,,

Рис. 9.13

линейные напряжения между соответствующими парами проводов и фазные напряжения

нагрузки ,,,-соответственно равны друг другу. Другими словами, при

соединений треугольником линейные напряжения равны соответствующим фазным

напряжениям. Поэтому фазные токи нагрузки определяются через заданные фазные ЭДС и

сопротивления нагрузки по соотношениям:

Линейные токи ,,определяются через фазные по первому закону Кирхгофа:

,,

Покажем, что при симметричной нагрузке линейный ток в раз больше фазного,

т. е.

Таким образом, линейный ток враз больше фаз­ногои на 30°отстает от него.

Рис. 9.14

Аналогично можно получить, что линейный ток илиотстает соответственно от фазного

токаилии враз больше последнего.

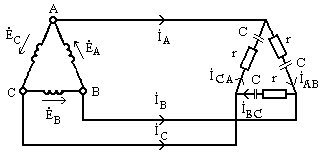
Рис. 9.15

Эти соотношения проще запомнить, если построить векторно-топографическую диаграмму, показанную на рис 9.14.Следует отметить, что фазные токи генератора, если их

положительное направление выбрать совпадающим с положительным направлением ЭДС, будут равны фазным тикам нагрузки одноименных фаз.

Пример 9.2. Вцепи рис. 9.15определить фазные и линейные токи, если r =25Ом, С = 100мкФ

и e_A(f)=141sin(400е+30°)В.

Решение

Запишем действующее значение ЭДС фазы Агенератора в комплексной форме

В. Вычислим емкостное сопротивление

Ом

Так как , то

A

Токбудет отставать от токана 120^й, а ток будет опережать токна 120°,поэтому

A

A

Линейные токи найдем на основании первого закона Кирхгофа:

По результатам вычислений построена векторно-топографическая диаграмма,

показанная на рис. 9.16.

3.Обмотки генератора соединены в звезду, а сопротивле­ния нагрузки соединены в треугольник, 'как показано на рис. 9.17. .

Рис. 9.16 Рис. 9.17

Если принять, что фазная ЭДС фазы Агенератора име­ет нулевую начальную

,то

Фазные токи в фазах нагрузки найдем .по закону Ома:

Линейные токи найдем по первому закону Кирхгофа:

Найденные величины иллюстрируются векторно-топографической диаграммой, приведенной на рис. 9.18,где ось ве­щественных чисел направлена по вертикали.

Рис. 9.18Рис. 9.19

Пример 9.3.В цепи рис. 9.19определить фазные и линей­ные токи при Х_L=22 Ом и фазном напряжении генератора.