fisika_samrab

НЕКОТОРЫЕ ПОЛЕЗНЫЕ СВЕДЕНИЯ

ФИЗИЧЕСКИЕ КОНСТАНТЫ

ПРИСТАВКИ И МНОЖИТЕЛИ для образования десятичных кратных и дольных единиц

50

Введение

В физике и других естественных науках весьма часто приходится производить измерения различных величин (например, длины, массы, времени, температуры, электрического сопротивления и т.д.). Измерить величину – значит сравнить ее с однородной величиной, принятой за единицу измерения (эталон).

Конечно, на самом деле при измерениях мы никогда не применяем эталоны единиц физических величин. Обычно мы пользуемся измерительной аппаратурой, которая проградуирована по эталонам.

Все измерения можно разбить на два типа: прямые измерения и косвенные. Прямыми измерениями называются такие, при которых интересующая нас физическая величина измеряется непосредственно. Примером прямых измерений служат измерения длины, массы, интервалов времени, температуры. Косвенными измерениями называют такие, в результате которых определяемая физическая величина вычисляется по результатам прямых измерений других величин, связанных с искомой некоторой формулой. Например, необходимо измерить плотность тела, имеющего форму цилиндра. Пользуясь зависимостью между плотностью ( ), массой (m) и объемом цилиндра, получим:

где D – диаметр цилиндра, h – высота цилиндра,

m, D, h – результаты прямых измерений.

К косвенным измерениям прибегают в том случае, когда интересующая нас величина не может быть измерена непосредственно (например, момент инерции тела, коэффициент внутреннего трения) или когда прямые измерения дают недостаточно надежные результаты.

Общей чертой любых измерений является то, что ни одно из измерений невозможно произвести абсолютно точно, т.е. результат измерения всегда содержит какую-то ошибку (погрешность).

Погрешности, допускаемые при измерениях, могут быть систематические и случайные.

Систематическими называются погрешности, обусловленные одной и той же причиной, которая чаще всего известна заранее. Обычно при многократных измерениях физической величины систематическая ошибка имеет одно и тоже значение, т.е. систематически повторяется. Например, шкала измерительной линейки неравномерная, стрелка амперметра при отсутствии тока через него не стоит на нуле и т.д. Систематические ошибки можно устранить, либо учитывая их в виде поправок к показаниям приборов, либо проверив данные приборов по эталонам. Систематических ошибок можно избежать лишь при внимательном и критическом отношении к методам исследования.

3

Случайными называются ошибки, вызванные весьма большим числом отдельных причин, действующих в каждом отдельном измерении различным образом. Органы чувств человека несовершенны. Любой измерительный прибор изготовлен с некоторой ограниченной точностью, определяемой уровнем приборостроительной техники, существовавшей в период изготовления прибора. Градуировка и проверка измерительной аппаратуры так же, как и любой другой измерительный процесс, не могут быть проведены абсолютно точно. Во время проведения измерения и измерительная аппаратура, и измеряемая величина подвергаются огромному количеству разнообразных воздействий извне (изменение температуры, давления, влажности, порывы ветра, сотрясения здания, вызванные движением транспорта и т.д.). Случайные ошибки устранить нельзя, но можно свести их к минимуму. В дальнейшем мы будем считать систематические ошибки устраненными и рассматривать только случайные ошибки.

Третий тип ошибок, с которыми приходится иметь дело, – грубые ошибки, или промахи. Под промахом понимается ошибка, сделанная вследствие неверной записи показаний прибора, неправильно прочитанного отсчета и т.д. Источником таких ошибок является недостаток внимания экспериментатора. При всяком опыте промахи должны быть исключены, основной способ их устранения – величайшая тщательность и внимание во время работы.

ОШИБКИ ПРЯМЫХ ИЗМЕРЕНИЙ

Пусть проделано n измерений какой-либо величины, истинное значение которой равно X; x1, x2, x3, … xn – результаты отдельных измерений. Среднее арифметическое из этих результатов, т.е.

является наиболее близким к истинному значению X.

Разности х1, х2, х3, …, хn между средним значением хср измеряемой величины и значениями x1, x2, x3, …, xn , полученными при отдельных измерениях, т.е.

хср – х1 = х1, хср – х2 = х2,

хср – х3 = х3,

……………..,

хср – х n = х n,

называются абсолютными ошибками или погрешностями отдельных измерений и могут быть положительными или отрицательными.

4

Среднюю абсолютную ошибку измерений определяют как среднее арифметическое абсолютных значений (модулей) отдельных ошибок т.е.

Она показывает, какую часть измеряемой величины составляет средняя абсолютная ошибка.

Относительные ошибки являются величинами безразмерными. Истинное значение

Х = хср хср.

Такая запись показывает, что истинное значение измеряемой

величины находится в интервале от хср – хср до хср + хср.

Если точность прибора недостаточна и при любом числе измерений получается одно и тоже число или измерения выполнены один раз, то среднюю абсолютную ошибку считают равной половине цены наименьшего деления прибора. Так же поступают, если средняя абсолютная ошибка меньше половины цены деления прибора.

Если значения какой-то величины измерены заранее, то абсолютная ошибка этой величины равна половине единицы наименьшего разряда, представленного в числе.

Например, если дана масса тела m = 932 г, то m = 0,5 г.

ОШИБКИ КОСВЕННЫХ ИЗМЕРЕНИЙ

Пусть для нахождения искомой величины Х пришлось измерить

какие-то величины x1, x2, x3, … xn. Величины Х, x1, x2, x3, … xn связаны функциональной зависимостью

Х = f (x1, x2, x3, … xn).

Как скажутся ошибки прямых измерений x1, x2, x3, … xn на конечном результате? Средняя абсолютная ошибка находится по правилам дифференцирования, если заменить значок дифференциала d значком ошибки , выбрать знаки таким образом, чтобы величина ошибки была максимальной.

5

Таким образом, для нахождения средней абсолютной ошибки надо:

1)продифференцировать расчетную формулу;

2)заменить значок дифференциала d значком ошибки ;

3)заменить все знаки «–», стоящие перед выражениями, содержащими абсолютные ошибки, на знак «+».

ПРИМЕР 1

х = а + b.

Измерив величины а и в, вычислим их средние значения и средние абсолютные ошибки а и b.

Продифференцируем выражение

d x = d a + d b.

Заменим знаки d на

x = a + b.

Абсолютная ошибка суммы равна сумме абсолютных ошибок слагаемых.

Абсолютная ошибка разности равна сумме абсолютных ошибок уменьшаемого и вычитаемого.

ПРИМЕР 3

x = 3 a b – 4 c3;

dx = 3 a db + 3 b da – 12 c2 dc;x = 3 a b + 3 b a + 12 c2 c;

Для нахождения относительной ошибки результата необходимо:

1)прологарифмировать функцию, определяющую зависимость искомой величины от измеряемых величин;

6

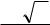
2)взять полный дифференциал от полученного выражения по всем переменным (переменными считать те величины, которые были измерены в ходе лабораторной работы);

3)заменить значки дифференциала d значками ошибки , все частные ошибки взять со знаками «+».

ПРИМЕР 4 8a b x c3 .

Воспользуемся правилом нахождения относительной ошибки. Прологарифмируем расчетную формулу

n x n 8 n a 12 n b 3 n c.

Продифференцируем полученное выражение

Заменим знак дифференциала d знаком ошибки и знак «–» на знак «+», получим

Теперь можно найти абсолютную ошибкух = х х.

ПРИМЕР 5

x = 2 a (b 2 – c 2).

Находим относительную ошибку

n x n 2 n a n (b2 c2 );

Найдем абсолютную ошибку выражения (b 2 – c 2) по правилам нахождения абсолютной ошибки

(b 2 – c 2) = 2 b b + 2 c c.

7

q = q q.

ПРИМЕР 7

V = R2 H;

n V n π 2 n R n H;

dVV 2 dRR dHH ;

γV VV 2 RR HH ;V = V V.

ПРИМЕР 8

x 2a b (3c2 2f); 5f

n x n 2 n a n b n (3c2 2f) n 5 n f;

х = х х.

Если исходное выражение представляет собой алгебраическую сумму нескольких слагаемых, то легче находить сначала абсолютную ошибку, а потом относительную. Если же исходная формула – произведение нескольких сомножителей, то лучше найти сначала относительную ошибку, а затем уже абсолютную.

Как видно из этих примеров, относительная ошибка произведения равна сумме относительных ошибок отдельных сомножителей, причем каждая из этих ошибок умножается на модуль показателя степени соответствующего сомножителя.

8