4 Силовой анализ механизма

4.1 Силовой анализ механизма по группам Ассура

Задачей силового анализа является определение уравновешивающей силы и реакций действующих в кинематических парах.

Для начала силового анализа необходимо определить значения всех сил действующих на механизм.

Сила полезного сопротивления:

Силы инерции:

Силы тяжести:

Моменты инерции:

Силовой анализ выполняется начиная с крайне группы.

Разделим механизм на группы Ассура:

Первая группа 5-4.

Перерисуем отдельно группу 5-4 в масштабе 1:10. В соответствующих точках обозначим силы действующие на группу.

Сила полезного сопротивления направлена навстречу скорости ползуна 5. Главные векторы сил инерции звеньев 4-5 направляем согласно плану ускорений в сторону, противоположным соответствующим ускорениям. Моменты инерции направлены противоположно соответствующим угловым ускорениям. Перпендикулярно направляющим ползуна изображаем реакцию стойки на ползун , также на 4 звено действует сила со стороны 3 звена .

Составим уравнение равновесия относительно точки С, найдем реакцию :

Неизвестную силу находим из многоугольника сил, который составляем согласно векторному уравнению:

Для построения плана сил группы 5-4 выбираем масштабный коэффициент:

Определим длины соответствующих векторов:

Для того чтобы найти значение реакции соединяем начало многоугольника с его концом т.к. сумма всех сил должна равняться нулю по условию равновесия . Замерим получившийся отрезок и умножим его на масштабный коэффициент сил:

Аналогичным образом проведем силовой анализ группы 3-2.

Масштаб группы 1:10.

На 3 звено со стороны звена 4 будет действовать сила равная по модулю силе , но противоположна ей по направлению. В опоре коромысла О₁ присутствует реакция опоры которую разложим на составляющие , где направлена вдоль звена, а перпендикулярно звену. На звено 2 действует сила со стороны вещего звена 1 которую также разложим на составляющие , где направлена вдоль звена, а , перпендикулярно звену.

Составим уравнение равновесия для 3 звена относительно точки В:

Составим уравнение равновесия для 2 звена относительно точки В:

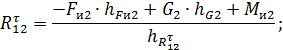
Составим векторное уравнение для многоугольника сил группы 3-2:

Определим длины соответствующих отрезков:

Построив многоугольник сил группы 3-2 определим значения сил , и :

Рассмотрим ведущее звено:

Масштаб звена 1:10.

На первое звено действует сила равная по значению силе и противоположна ей по направлению. Уравновешивающая сила, приложенная к ведущему звену, направлена в сторону вращения 1 звена.

Составим уравнение равновесия и определим уравновешивающую силу:

4.2 Метод жесткого рычага Жуковского

Метод заключается в том, что план скоростей поворачиваем на 90⁰. В соответствующих точках прикладываем действующие силы и составляем уравнения равновесия относительно полюса. Из которого определяем уравновешивающую силу. Моменты инерции необходимо заменить эквивалентными парами сил.

Приведение моментов инерции к эквивалентной паре сил:

Уравнение равновесия относительно полюса:

Проверка на сколько процентов отличаются полученные двумя методами значения:

Отклонения является допустимым.

Определим уравновешивающий момент: