
3
.pdfданныханализаиразработкидлярешетокТеория КузнецовС.О. решеткииПолурешетки3.Тема
1p.3ÄÀÒ
ПуВерстьхняя(P, ≤грань) - частичноподмно-упоржестваядоченное множество и A P . |
|
|
A P есть множество |
Точная (или наименьшая){b верхняяP | a Aграньb ≥ aподмножества}. |
|
элементнаименьший |
|
1. |
b верхней грани A (если он существует): |
A P
åñòü
2.
a A b ≥ a,
Точнаяx верхняя(P a граньxмножества≥ a) x ≥ b. |
|
.точнойsup(A)поДвойственнообознадмночаетсжествадля |
(наибольшей)A называетснижнейя такжграние супремумinf(A) |
A
è
A P
такжназываетсякоторая,
имумин
A.
2p.3ÄÀÒ
Верхняя грань подмножества A P есть множество |
|
Точная (или наименьшая){b верхняяP | a Aграньb ≥ aподмножества}. |
|
элементнаименьший |
|
1. |
b верхней грани A (если он существует). |
A P
åñòü
2.
a A
x P
b ≥ a,
( a A
x ≥ a) x ≥ b
.
3p.3ÄÀÒ
полурешеткЧастично-упоройядоченное,еслидлямнолюбойжествопары(SL,элементов≤) азываетсмножяестваверхней |
|
supсупремумсуществуют |
x, y SL |
инДвойственноимума: для нижней{x,полурешеткиy}. |
относительноопределяемой, |
полурешеткЧастично-упоройядоченное,еслидлямнолюбойжествопары(SL,элементов≤) азываетсмножяестванижней |
|
infимуминсуществуют |
x, y SL |
|
{x, y}. |
4p.3ÄÀÒ
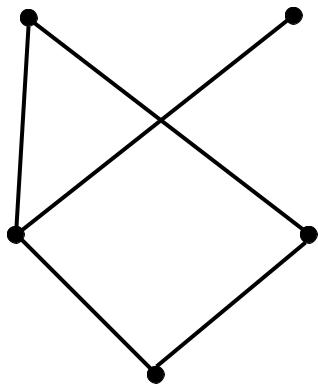
полурешетканижняя
5p.3ÄÀÒ
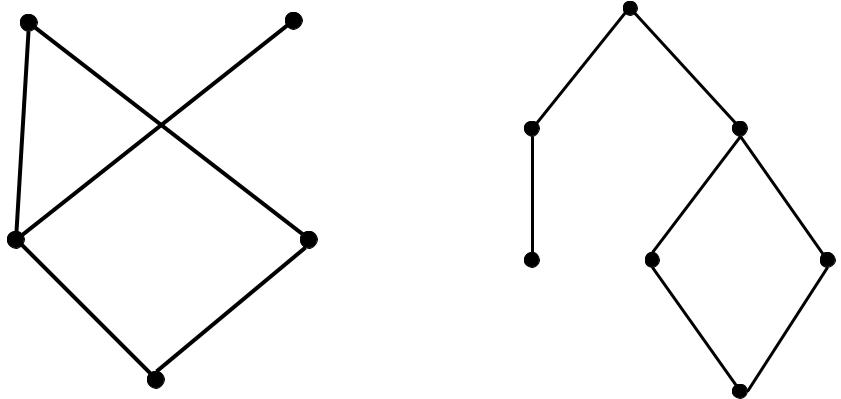
полурешетканижняя |
полурешеткаверхняя |
6p.3ÄÀÒ
любойЧастичнопары-упорэлементовядоченное множество (L, ≤) |
|
inf |
x, y L существуют |
|
{x, y}. |
называется решеткой, если для супремум sup{x, y} è èí èìóì
7p.3ÄÀÒ
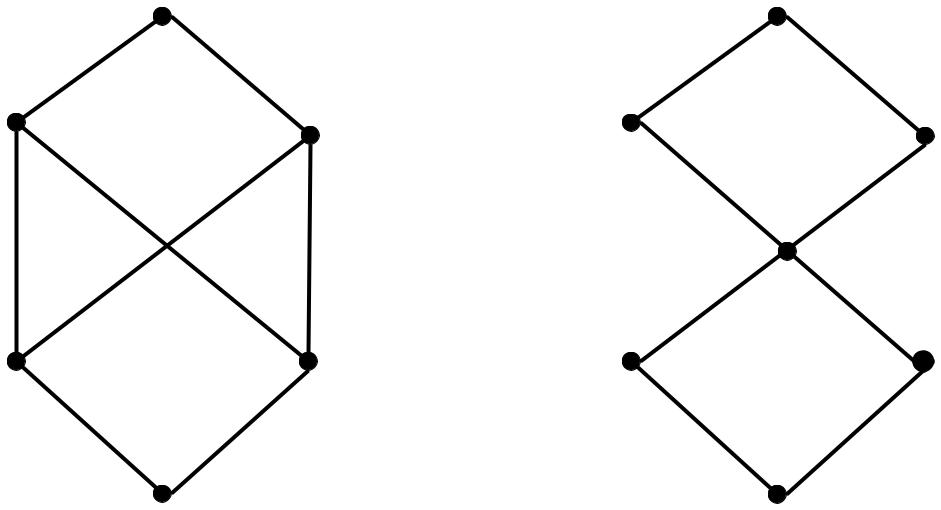
нижнейнеявляетсянепорядок |
частичный |
порядок |
полурешеткойверхнейнечастичный |
решеткойявляющийся |
|
8p.3ÄÀÒ
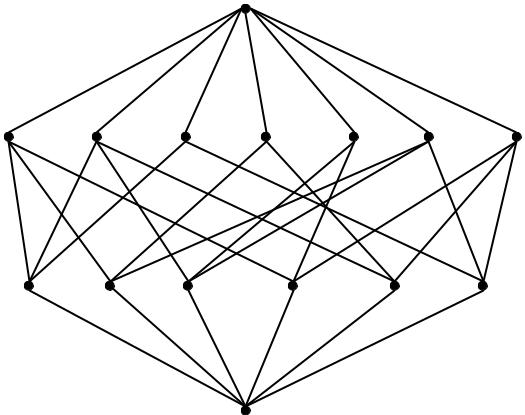
A = {1, 2, 3, 4}
1234
123|4 |
124|3 |
13|24 |
14|23 |
234|1 |
|
12|34 |
|||
|
134|2 |
|||
|
|
|
|
12|3|4 |
13|2|4 |
14|2|3 |
23|1|4 |
24|1|3 |
34|1|2 |
|
|
|
1|2|3|4
9p.3ÄÀÒ
Теореманекдвеоторогооперации. ПроизвольноечастчногопормноядкжаествотогдаLиявляетстолькоятогрешеткдаогойдаотносительнонанемзаданы
и , удовлетворяющие следующим свойствам для любых
x,L1y, z L:
L2 L3 L4
x x = x, |
x x = x (идемпотентность) |
|||
x = x (x y) = x (x y) |
(поглощение) |
|||
x y = y x, |
x y = y x |
(коммутативность) |
||
x (y z) = (x y) z, |
x y z = (x y) z |
|||
(ассоциативность)
10p.3ÄÀÒ
