Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный физико-технический университет (МФТИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лекции

.pdf

Скачиваний:

Добавлен:

03.06.2015

Размер:

1.71 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 109 10 > Следующая >>>

k 2	2		( ) .
	c 2	0

Это уравнение определяет только модуль волнового вектора, что значит, что закон дисперсии не зависит от направления распространения волны, как и должно быть в изотропной среде.

9.3.2. Одноосный кристалл

Важный случай анизотропных сред дают одноосные кристаллы. В таких средах тензор диэлектрической проницаемости может быть записан в следующем диагональном виде

0		0	0

0		0	0

	0	0	e

где 0 e . Если 0 e , то говорят, что это отрицательный одноосный кристалл, в случае 0 e - это положительный одноосный кристалл.

Ось, вдоль которой диэлектрическая проницаемость	равна	e , называется
оптической осью. Если ввести орт оптической оси e , то	вектор	электрической
индукции можно представить как
D 0 ( , k )E e ( , k ) 0 ( , k ) (e E )e .		(11)

Заметить можно, что если вектор электрического поля направлен нормально к оптической оси (лежит в плоскости, нормальной к оптической оси), то (e E ) 0 и для такой волны

D 0 ( , k )E .

Следовательно, волна распространяется как в изотропной среде. Эти волны (так поляризованные, если понимать поляризацию как направление вектора электрического поля) называют обыкновенными волнами. Если вектор электрического поля направлен параллельно оптической оси, то есть, E (e E )e E e , то из (11) следует, что

D 0 ( , k )(e E )e e ( , k ) 0 ( , k ) (e E )e e ( , k )(e E )e e ( , k )E .

Так поляризованная волна распространяется как бы в изотропной среде, но с другой диэлектрической проницаемостью, которая равна e .

Во всех этих рассуждениях о поляризации волн не использовался вектор, задающий направление распространения n .

Подставить надо D из (11) в уравнение (5) что приведет к уравнению

0 E e 0 (e E )e n 2 E n (n E ) .

Это однородная система линейных уравнений относительно трех компонент вектора E , ненулевым решения которой возможны, если соответствующий определитель будет

(e E ) 0 , чтобы систему уравнений (12)

e n 2

равен нулю. Так можно получить частный случай уравнения Френеля. Немного проще можно поступить.

Умножив это уравнение на n , получим

	0	(n E )	e	0	(e E )( n e ) n 2	(n E ) (n n )( n E ) .
Или
			0 (n E ) e 0 (n e)(e E ) 0 .				(12.1)

Умножив это уравнение на e , получим

0 (e E ) e 0 (e E ) n 2 (e E ) (n e )( n E ) ,

или

(

n 2 )( e E ) (n e )( n E ) 0 .

(12.2)

Система уравнений (12) есть система однородных линейных уравнений относительно двух неизвестных (n E ) и (e E ) .Ненулевые решения существуют, если определитель этой системы равен нулю:

det

(n e)e 0

(n e)		0 .

0

Или,

	0	(	e	n 2 )	e		0	(n e ) 2	0 .	(13)
	0		e		e		0

Можно ввести угол, под которым волна (фазовый фронт волны) распространяется по

отношению к оптической оси ,

так что (n e )

n cos . Тогда ряд преобразований

(

n 2 )

n 2

cos 2

n 2

n 2 cos 2

2 cos 2

n 2 (1 cos 2 )

n 2 cos 2

n 2 sin

n 2

cos 2

0 .

Разделить надо это уравнение на

n 2 , что даст

sin 2

cos 2

(14)

n 2

Это дисперсионное соотношение для волны, с ненулевыми проекциями (n E )

и (e E )

электрического поля, которое показывает, что «показатель преломления» или волновое число зависят от направления распространения волны в одноосном кристалле. Волна, отвечающая такому дисперсионному соотношению, называется необыкновенной волной.

Для обыкновенной волны, для которой не приводила бы к противоречию, должно выполняться условие поперечности волны (n E ) 0 , тогда из выражения

0 E e 0 (e E )e n 2 E n (n E ) ,

следует

0 E n 2 E ,

идисперсионное соотношение для обыкновенной волны будет иметь вид

0 ( , k ) n 2 .

Следовательно, обыкновенная волна поперечная и распространяется как в изотропной среде с диэлектрической проницаемостью 0 ( , k ) .

Упражнение 1. Получить дисперсионное уравнение типа (6) для магнитного диэлектрика, когда ( , k ) не сводится к единичному тензору, умноженному на скаляр.

Упражнение 2. Используя принцип Гюйгенса, надо построить ход лучей при их преломлении в положительном и отрицательном одноосном кристалле.

Упражнение 3. Доказать формулу (11)

D 0 ( , k )E e ( , k ) 0 ( , k ) (e E )e .

Упражнение 4. Исходя из уравнения

0 E e 0 (e E )e n 2 E n (n E ) .

получить уравнение Френеля для одноосного кристалла.

Упражнение 5. Исходя из уравнения

det s 2 ij si s j 1 ij 0 ,

найти направления потока энергии в одноосном кристалле.

Упражнение 6. Показать, что s n 1 .

Дополнение (к Упражнению)

Лекция 10. (19.11.2010)

Первые 30 минут посвящены были выводу дисперсионного уравнения для необыкновенной волны в одноосном кристалле. Этот вывод на прошлой лекции не успел рассказать.

Волны в волноводных структурах надо обсудить. Волну можно направлять вдоль границы раздела двух сред. Что уже рассмотрено было. Известны волноводы в виде металлической трубки цилиндрического или прямоугольного сечения. Внутри таких металлических трубок может существовать стоячая в поперечном направлении волна, но распространяющаяся вдоль оси трубки. СВЧ-техника использует такого рода волноводы. Для освещения закрытого помещения можно использовать (металлический или пластиковый) короб с зеркальными внутренними поверхностями.

Диэлектрический стержень в окружении диэлектрической же среды при определенных условиях может быть волноводом. Весьма качественно можно говорить об отражении волны (лучей, если волновод достаточно большого диаметра или поперечного размера) от границы раздела двух диэлектрических сред, так чтобы в поперечном направлении образовалась стоячая волна.

Прообразом тонкопленочных волноводов является пластина диэлектрика, на диэлектрической подложке и накрытая диэлектриком. Воображаемая модель такого волновода это пластина неизменной толщины, бесконечно протяженная в двух направлениях – планарный волновод. Для учебных целей полезно планарный волновод подробно рассмотреть.

10.1. Планарный волновод.

Распределение диэлектрической проницаемости вдоль оси Х задается кусочнонепрерывной функцией

3		,	x h
	2 ,
( x )			0 x h
	1	,	x 0

	Рис.1.
				3
Распределение		диэлектрической		h
Распределение		диэлектрической
проницаемости	в	случае	планарного	2
волновода. Волноводный слой (2) на				2	Z
волновода. Волноводный слой (2) на					Z
подложке (1) с покровным слоем (3).
				1

Рассматриваться будет ТЕ волна. Как пример. Волновое уравнение имеет вид:

2 E y	2 E y	k 2	x E		0,	(1)
				y
z 2	x 2	0

где k0 = /c . Компоненты вектора напряженности магнитного поля для этой волны связаны с Ey соотношениями:

H x	i	E y	, H z		i	E y	.

	k 0	z			k 0	x

На границе раздела x 0 непрерывны Ey, Hx				и Hz . Краевые условия, отбирающие из

всех решений (1) только те, которые соответствуют поверхностным волнам, имеют вид:

lim E y ( ,x, z ) 0,	lim E y	/ x 0.	(2)
\|x\|	\|x\|
В силу трансляционной симметрии вдоль оси z	E y ( , x , z ) следует выбрать в форме

E y ( ,x , z ) ( x ) exp{ i ( ) z},

где ( ) постоянная распространения. Отсюда и из (1) следует уравнение для ( x ) поперечного профиля электрического поля:

		,	xx	[ k 2	( ,x ) 2 ] 0,		(3)
			xx	0
при этом ( x )	и , x ( x )	непрерывны при x 0				и обращаются в нуль при x.

Принимая во внимание вид функции ( x ) , можно рассматривать (3) в каждом однородном слое и затем сшить найденные решения на границах раздела используя (2).

Пусть x 0 , тогда (3) переписывается как

, xx (k 02 1 2 ) 0 .

Чтобы решение этого уравнения второго порядка с постоянными коэффициентами

удовлетворяло бы краевому условию при x , надо потребовать					q 2 ( 2 k 2	1	) 0
					0	1
и записать решение как
	(1) ( x ) A exp( qx ),						(4)
				1
где и ради определенности выбрано				q > 0 (второе фундаментально решение
отброшено, поскольку оно отвечает экспоненциально растущей функции).
При x h уравнение (3) записывается как
,	xx	(k 2	3	2 ) 0 .
	xx	0	3

Для того, чтобы удовлетворить краевым условиям на бесконечном удалении от волновода, надо положить p 2 ( 2 k 02 3 ) 0 и выбрать затухающее решение, так что

( 3) ( x ) A	3	exp( px ) .	(5)
	3

Здесь p > 0. Внутри волноводного слоя уравнение (3) записывается как

, xx (k 02 2 2 ) 0 .

Тут нет условия, которое определяет знак постоянного коэффициента (k 02 2 2 ) .

Можно выбрать знак плюс и, решив задачу полностью, найти, что дисперсионное соотношение существует. Можно выбрать знак минус и убедиться в конце решения задачи, что полученное при этом дисперсионное соотношение не имеет решений. Но можно и не решая задачи сразу понять, что отрицательное значение коэффициента

(k 02 2 2 ) отвечает паре поверхностных волн, каждая из которых локализована около

границе при x 0 и x h . В одной из предыдущих лекций было установлено, что поверхностных волн ТЕ типа на границе обычных диэлектриков нет. Следовательно, и пары поверхностных волн не может быть. По этой причине никто и не рассматривает

этот случай. Остается положить (k 2	2	2 ) 0 , или иначе,			k 2	2	2	2	0	. Решение
0	2				0	2
уравнения (3) в области 0 x h является функция ( 2 ) ( x )
( 2 ) ( x ) A	2	exp( i x ) B	2	exp( i x ) .						(6)
	2		2

Условия непрерывности приводят к системе уравнений:

( x ) и , x ( x ) на границах раздела x 0 и x h

A1 A2 B 2 ,	pA1 i ( A2 B 2 ),
A3 A2 exp( i h ) B 2 exp( i h ),		(7)
qA3 i [ A2	exp( i h ) B 2 exp( i h )].

Из первых двух уравнений следует, что

	1			p			1			p
A2		A1	1		,	B 2		A1	1		.

	2			i			2			i

Из двух последних уравнений можно выразить A3 двумя способами. А именно,

i h

A1 1

а из последнего уравнения системы (7) следует, что

i h

Следовательно,

i h

Если ищется волна с ненулевой амплитудой, то A1 не равно нулю и можно разделить полученное выражение на A1 . В результате будет получено дисперсионное соотношение для ТЕ волны, локализованной в волноводном слое.

i h

0 .

Собрав подобные члены, можно переписать это выражение как

i h

Или,

i 2 h

0 .

Коэффициенты в скобках стоящие в нуль не обращаются, потому можно, не опасаясь потерять что-либо, разделить первое слагаемое на второе, что приводит к выражению

	1 p / i		1 i / q
e i 2 h				1	0 .	(8)

	1
		p / i	1 i / q

В это выражение параметры q и p входят не симметрично. Но выбор направления оси Х произволен, и выбор обозначений для q и p произволен. Так что было бы изящно иметь первое слагаемое в виде

	1 p / i		1 q / i
e i 2 h				.

	1
		p / i	1 q / i

Этой симметрии выражения (8) можно достичь, если умножить (8) и разделить одновременно на q / i . Тогда (8) переписывается как

	1 p / i		1 q / i
e i 2 h				1 .	(9)

	1
		p / i	1 q / i

Стоит заметить, что каждый множитель в скобках ест комплексное число по модулю равному единице. Следовательно, можно вести вещественные фазы

1 p / i

p ,

1 q / i

q .

p / i

1 q / i

Тогда выражение (9) представляется как

e	i 2 h	e	i p	e	i q	e	i 2 h i p i q	1 e	2 im	,

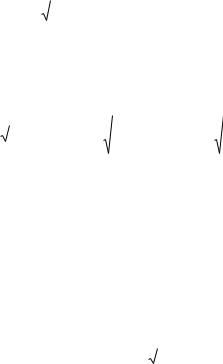
где m - целое (положительное) число или нуль. Следовательно, дисперсионное соотношение представляется как

2 h p q

2 m .

(10)

Если бы волновод был пустой с металлическими поверхностями, то условие образования стоячей волны внутри такого волновода выражалось бы уравнением

2 h 2 m .

Но, поскольку волновод диэлектрический, то появляются дополнительные фазовые сдвиги (эффект Гуса-Хенгена), обусловленные полным внутренним отражением волны на границах раздела диэлектрических сред.

Дисперсионное соотношение (9) иногда переписывают как

tan( h )	( p q )	.	(11)

	2 pq
Из (10) как и из (11) можно получить еще одно представление для
дисперсионного соотношения. Из определения фаз можно найти, что
tan( p / 2 ) p / ,	tan( q / 2 ) q / ,		(12)

Известно, что в линейной интегральной оптике дисперсионное соотношение для ТЕмод можно записать в универсальной форме, если ввести эффективный показатель

преломления e	/ k 0 и параметры
						, b	e 1			a	1 3	.
	V k	0	h	2	1				,

							2	1			2 1

В рассмотренном здесь случае универсальное выражение для дисперсионного соотношения имеет вид

b a

m .

(14)

V 1 b arctan

arctan

1 b

В координатах (V , b ) дисперсионные соотношения представляются ветвями функции b (V , m ) - для каждого целого числа m своя кривая.

Надо нарисовать эти кривые

Рассказ далее про моды волновода, частоты отсечки и количество мод в волноводе в зависимости от его параметров.

b (V ( m ) , m ) 0 ,

это уравнение, определяет частоты отсечки. Из (14) тогда следует, что

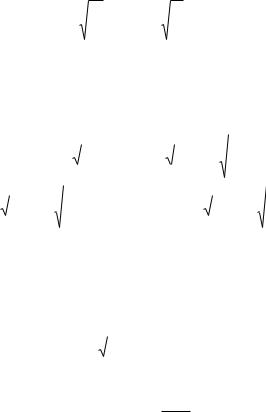
V ( m ) arctan			m .
		a

Упражнение 1. Найти дисперсионное соотношение для ТМ воны в планарном волноводе с диэлектрической проницаемости заданной кусочнонепрерывной функцией.

Упражнение 2. Найти дисперсионное соотношение для волновода с диэлектрической проницаемости заданной кусочнонепрерывной функцией следующего вида

1 ,				x 0,
( x )	3	( 2	3 ) exp( x / h ),	x 0.

Упражнение 3. Найти дисперсионное соотношение для симметричного волновода с диэлектрической проницаемости заданной кусочнонепрерывной функцией следующего вида


		3	( 2	3 ) exp( x / h ),	x 0,
( x )	3		( 2	3 ) exp( x / h ),	x 0.
	3		( 2	3 ) exp( x / h ),	x 0.

Дополнение (Вывод нормированного дисперсионного соотношения)

Уравнение (10) с учетом (12) можно переписать как

					h arctan									p	arctan						q	m .											(10*)
					h arctan										arctan							m .											(10*)

Из	определения 2				k			2		2	2			и	эффективной											диэлектрической проницаемости
								0		2
e	/ k 0	следует, что h							можно записать как

																												2 e			=
						h k						0	h	2		e	k	0	h			2			1			2 e
						h k							h				k		h
																												2	1
																												2	1

													2 1 1 e																	1		e 1		.
		k	0	h			2				1		2 1 1 e							k			0	h			2		1			e 1
		k		h																k				h
														2	1																	2	1
														2	1																	2	1

В этом выражении присутствуют параметры подожки и волноводного слоя, и величина, показывающая как меняется эффективная диэлектрическая проницаемость по отношению к окружающим волновод средам. Так вводятся два параметра

						b	e 1	,
V k	0	h	2	1	,		e 1
V k		h			,
							2 1
							2 1

спомощью которых набег фазы в поперечном направлении есть

h V 1 b .

Надо заметить, что параметр b меняется от нуля до единицы. Далее, можно записать

p	e	1	.
			.
	2	e

Числитель легко выражается через параметр b : e 1 b ( 2 1 ) . Тогда

	p				b (				2 1 )											b ( 2 1 )														b ( 2 1 )

						2			e									( 2		1 ) 1 e												( 2		1 ) ( e					1 )
									b ( 2						1 )															b								b		.
				(		2				1		) (					e			1	)		1 (			e				1	)(		2		1	) 1	1 b			.
						2				1							e			1						e				1			2		1
Аналогично,
		q						e 3									e 1 1 3											b ( 2 1 ) ( 1 3 )

							2 e												2 e											( 2 1 ) 1 e
			b (				2				1		) (				1			3	)		b (				1			3	)(		2		1	) 1		b a
							2				1						1			3							1			3			2		1						.
					(			2				1		)		1			e				1 (			1				e	)(		2		1	) 1		1 b			.
								2				1				1			e							1				e			2		1
где введен параметр
																						a		1	3				.
																						a							.
																								2	1

Подстановка полученных выражений в (10*) дает (14).

Дополнение (к Упражнению)

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 109 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
03.06.2015845.46 Кб53Лебедев, Колоколов. ИГМФ.pdf
#
03.06.2015933.51 Кб9Лекции - Раздел 1.pdf
#
01.03.2025208.38 Кб0Лекции ОИ.doc
#
03.06.201514.11 Mб13Лекции по физкинетике.PDF
#
03.06.2015386.05 Кб39Лекции по философии (Семенов) 2006-2007.doc
#
03.06.20151.71 Mб22Лекции.pdf
#
03.06.201583.97 Кб42Лекция Потребности и мотивы.doc
#
03.06.20151.29 Mб29Лекция 1 - конспект.pdf
#
03.06.20151.87 Mб58Лекция 10 - Неметаллические материалы.pdf
#
03.06.2015910.58 Кб8Лекция 10.pdf
#
03.06.20152.45 Mб49Лекция 12 - Наноматериалы и УНТ.pdf