Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный физико-технический университет (МФТИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лекции

.pdf

Скачиваний:

Добавлен:

03.06.2015

Размер:

1.71 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 107 8 9 10 > Следующая >>>

могут быть переписаны как

i			H x		y E z z E y z E y ,
	c		H x		y E z z E y z E y ,
	c
				i			H y z E x x E z ,
							H y z E x x E z ,
				c
	i		H z				x E y y E x x E y ,
			H z				x E y y E x x E y ,
	c
i		~					y H z z H y z H y ,
		E x
	c	E x
	c
				i		~
							E y z H x x H z ,
				c			E y z H x x H z ,
				c
	i ~						x H y y H x x H y .
			E z
	c		E z
	c

Можно увидеть, что эти уравнения распадаются на две группы:

 Для волн с напряженность полей E y ,

H x

и H z :

E y ,

i ~

H x x H z .

H x z

E y

H z

E y z

 Для волн с напряженность полей H y

, E x

и E z

i ~

E x z H y

E z x H y ,

H y

z E x

x E z .

(ТЕ)

(ТМ)

Уравнения (ТЕ) описывают волну, у которой вектор электрического поля перпендикулярен направлению распространения, и эта волна называется поперечной электрической волной или ТЕ-волной. Уравнения (ТМ) описывают волну, у которой вектор магнитного поля перпендикулярен направлению распространения, и эта волна называется поперечной магнитной волной или ТМ-волной. Существуют другие термины для этих типов волн. Так можно встретить для ТЕ-волны название s-волна или Н-волна. Для ТМ волны иногда используется название р-волна или Е-волна.

Из уравнений (ТЕ) и (ТМ) можно получить волновые уравнения. Так из (ТЕ)

2 ~

0 ,

(ТЕ.в)

( x z

) E y

E y

H x

z E y ,

H z

x E y .

Решив уравнение (ТЕ.в) напряженности магнитных полей можно определить с помощью двух оставшихся уравнений. Из (ТМ) следуют

1					1
z		z H y		x
z	~	z H y		x		~

E x			ic	z H y		,

			~

x				2		H y 0 ,	(ТМ.в)
	H y
				c 2

E z		ic			x H y .

			~

Поскольку комплексная диэлектрическая проницаемость есть функция (нормальной к границе раздела) координаты, в волновом уравнении для ТМ волны появляется производная от диэлектрической проницаемости.

Если среды могут быть магнитными, то учет магнитных проницаемостей надо сделать. В случае, если граница раздела резкая, то результат тривиально смотрится.

7.3. Поверхностные волны. Граница диэлектрик-проводник.

			~	1 ( ) ,
Пусть одна из сред (например, при x 0 ) чисто диэлектрическая, то есть 1 ( )
а вторя среда – проводящая, то есть при x 0	~	( ) / c . В высокочастотном
	2 ( ) i 4
пределе ( 1 ), проводимость чисто	мнимая	и	~	Будут
			2 ( ) 4 / c .

рассматриваться волны, локализованные около границы раздела, то есть к волновому уравнению надо добавить граничные условия, отвечающие исчезновению полей на бесконечности.

Рассматривается ТЕ волна. В области x 0 волновое уравнение принимает

вид

( 2 2 ) E

0 .

c 2

Граничные условия записываются как

при x ,

E y ( x , z , ) 0 и

H z

x E y

0 ,

следовательно, x E y

А при x 0 касательные компоненты полей непрерывны. То есть, непрерывными являются величины E y ( x , z , ) и x E y ( x , z , ) .

Поскольку вдоль оси Z среда однородная, решение этого уравнения надо искать в форме

E y ( x , z , ) ( x ) exp( i z ) ,

Так что амплитуды этой волны определяется уравнением

	, xx	( k 2	1	2 ) 0	.	(ПП.1)
	, xx	0	1
Функция ( x ) и ее производная непрерывны в точке					x 0 , и исчезает при удалении от

границы раздела сред. Решение с такими свойствами будет существовать, если

(k 02 1 2 ) 0

Обозначить можно ( 2

k 2

) q 2

и пусть q 0 . Затухающее на минус бесконечности

решение уравнения (ПП.1) записывается как

( x ) Ae qx .

(ПП.2)

В области x 0

волновое уравнение принимает вид

(

) E

0 ,

c 2

или

(

2 ) E

k 2

Из-за однородности среды вдоль оси Z решение этого уравнения надо опять искать в форме

E y ( x , z , ) ( x ) exp( i z ) ,

Так что амплитуды этой волны определяется уравнением

				, xx		( k 2	2 ) .	(ПП.3)
				, xx		p
Обозначить	( k 2	2 ) p 2	и положить		p 0		(а что будет, если	p 0 выбрать?) надо.
	p

Так что решение удовлетворяющее граничному условию на плюс бесконечности, записывается как

( x ) Be px . (ПП.2)

Непрерывность касательных компонент полей означает выполнение следующих условий

A B , qA pB .

Отсюда следует, что

( q p ) A 0 .

Это есть дисперсионное уравнение, оно показывает, как постоянная распространения

зависит от частоты . Но полученное уравнение решения не имеет. Следовательно, поверхностной волны ТЕ типа нет.

Картинку нарисовать и показать, что бы надо было «испортить», чтобы поверхностная волна появилась.

Рассматривается ТМ волна. В однородной					среде при x 0 волновое уравнение
(ТМ.в) переписывается как
( 2	2 ) H			2			H		0 .
( 2	2 ) H	y				1	H	y	0 .
x	z	y		c 2		1		y
				c 2
			63

Совпадение с уравнение для ТЕ волны. Рассуждая также, как и в случае ТЕ волны, решение этого уравнения записывается как

H y ( x , z , ) h ( x ) exp( i z ) ,

где

h ( x ) Ae qx , q 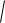2 k 02 1 .

Компоненты электрических полей

Ae qx i z ,

iqc

Ae qx i z .

В области x 0 волновое уравнение принимает вид

			2
( 2	2 ) H		p	H		0	,
		y			y
x	z		c 2

И его решение, удовлетворяющее граничному условию на плюс бесконечности есть

H	y	( x , z , ) Be px i z ,	p	k 2	2 .
	y			p

Компоненты электрических полей

c 2

ipc

E x

z H y

Be px i z ,

E z

x H y

Be px i z .

Непрерывность касательных компонент магнитного поля дает

A B .

Непрерывность касательных компонент электрического поля приводит к соотношению

iqc

ipc

B .

Следовательно

Это дисперсионное решение может иметь решение. Но не всегда.

Упражнение 1. Выразить вещественную и мнимую части постоянной распространения через проницаемости и проводимость.

В низкочастотном переделе проводимость вещественная величина ( ) 0 . Если определить

2	2		( ) ( )a 2 k 2 a 2 ,						2		2	( ) ( )b 2 k 2						b 2	,
	c 2				0						c 2						0
	c 2										c 2
то выше приведенные уравнения
			2 2	2	( ) ( ) ,								2		( )		.
			2 2		( ) ( ) ,										( )	0	.
				c 2										c 2		0
				c 2										c 2
переписываются как
			a 2 b 2 1 ,				ab (2						0	/ ) .
													0
Отсюда, a 4 a 2 2		0 и решение этого уравнения есть
						1		1
				a 2		1		1		1 4 2 .
				a 2						1 4 2 .
					2		2

Таким образом, можно для вещественной и мнимой части постоянной распространения записать

2	k 2	4		2			2	k 2	4	0	2
	0	1	0		1	,		0	1	0		1 .
		1			1	,			1			1 .
	2							2

Упражнение 2. Вывести волновые уравнения для ТЕ и ТМ волн с учетом намагниченности сред.

Упражнение 3. Вывести дисперсионное соотношение поверхностной волны ТМ типа для случая границы раздела диэлектрика и проводника, характеризуемого проницаемостью

~			4			2p
	( )	( )		( )	( )
	( )	( )		( )	( )	2
						2

Лекция 8. (29.10.2010)

Теперь надо рассмотреть преломление и отражение волны на границе раздела диэлектрических сред. Но лучше рассмотреть эту задачу в общем виде, когда возможно отрицательное преломление.

8.1. Преломление волн на границе раздела однородных сред.

Рассматривается граница раздела двух линейных изотропных однородных сред, такая, что при x 0 среда характеризуется диэлектрической проницаемостью 1 ( ) , магнитной проницаемостью 1 ( ) , а при x 0 среда характеризуется диэлектрической проницаемостью 2 ( ) , магнитной проницаемостью 2 ( ) . Уравнения Максвелла

rot E ( )

( ) H ( ) ,

rot H

( )E ( ) .

Распадаются на две системы уравнений

 Для волн с напряженность полей E y ,

H x

и H z

(это ТЕ волны):

E y ,

i ~

H z .

(ТЕ)

H x z E y

H z

E y z H x x

 Для волн с напряженность полей H y

, E x

и E z

(это ТМ волны):

i ~

E x z H y ,

E z x H y ,

H y z E x x E z .

(ТМ)

Надо условия непрерывности на границе раздела правильно записать. Из общих курсов физики (но можно все самому проверить или показать), что касательные компоненты полей непрерывны и нормальные компоненты электрической и магнитной индукции тоже непрерывны (если нет поверхностных токов проводимости или токов смещения).

 Для ТЕ волны условия сшивки при x 0	будут записывать как
E y (0 ) E y (0 ) ,	H z (0 ) H z (0 ) ,
1 H x (0 ) 2 H x (0 ) .			(8.1.1)
 Для ТМ волны условия сшивки при x 0		будут записывать как
H y (0 ) H y (0 ) ,		E z (0 ) E z (0 ) ,
1 E x (0 )		2 E x (0 ) .	(8.1.2)

Используя уравнения Максвелла (ТЕ) и (ТМ) можно условия сшивки переписать через одно из полей, то есть, как

 Для ТЕ волны условия сшивки при x 0 будут записывать как

E y (0 ) E y (0 ) ,

z E y (0 ) z E y (0 )

x E y (0 )

x E y (0 ) ,

(8.1.3).

 Для ТМ волны условия сшивки при x 0 будут записывать как

H y (0 ) H y (0 ) ,

z H y (0 ) z H y (0 )

x H y (0 )

x H y (0 ) ,

(8.1.4).

Сами волновые уравнения, учитывая однородность сред по обе стороны

границы раздела можно записать обычным образом

 Для ТЕ волны

( 2

2 ) E

0 .

(8.1.5)

c 2

 Для ТМ волны

( 2

2 ) H

0 .

(8.1.6)

Решения этих уравнений будут описывать распространение (гармонической) волны в том случае, если j j 0 . Случай, когда как диэлектрическая, так и магнитная

проницаемости положительные, обычно рассматривается в традиционных курсах. Здесь будет рассматриваться случай, когда 1 ( ) 0 , 1 ( ) 0 , но 2 ( ) 0 , 2 ( ) 0

. Для простоты предполагается, что все эти величины вещественные.

Преломление ТЕ-волн

Поскольку вдоль оси Z среды однородны, решение (8.1.5) можно искать в форме

E y ( x , z , ) ( x , ) exp{ iz ( )} ,

(8)

что дает для амплитуды уравнение второго порядка с кусочно-постоянными коэффициентами

		2			2
		2			2
							( ) ( ) 2 ( )			0 .			(9)
							( ) ( ) 2 ( )			0 .			(9)
	x		2	c	2
	x			c
Если определить
q 2 ( / c ) 2 n 2								2 ,	p 2 ( / c ) 2 n 2		2	,	(10)
						1				2

то решения уравнения (9), удовлетворяющее краевому условию, отвечающему падению волны с минус бесконечности и уход ее на плюс бесконечность (преломление на границе сред) записывается как

x 0 :

(1) ( x ) A exp( iqx ) B exp( iqx ) ,

x 0 :

( 2 ) ( x ) C exp( ipx ) .

(11)

Показатель преломления в (10) определяется формулой n 2 .

Здесь следует заметить, что знак параметра q можно выбрать как угодно. Конкретный выбор знака сказывается на интерпретации констант А и В которую из них считать амплитудой падающей волны, тогда другая константа есть амплитуда отраженной волны. Пусть здесь q 0 . В то же время, знак параметра p не определен,

пока не вычислено направление потока энергии. В данном случае согласно выбранному краевому условию, поток энергии должен быть направлено в положительном направлении оси Х.

Условия сшивки (8.1.3) в терминах				амплитуды ( x ) выражаются			двумя
равенствами:
(1)	( 2 ) ,	1	(1)	1	( 2 )	при x 0 .	(12)
(1)	( 2 ) ,	1	x	2	x	при x 0 .	(12)
		1	x	2	x

Подстановка в эти соотношения выражений (11) дает связь между постоянными интегрирования А, В и С:

	C		p	1			C		p
A		1		1	,	B		1		1	.
A		1			,	B		1			.
	2		q 2				2		q 2
	2		q 2				2		q 2

Полагая, что A E in есть амплитуда падающей на границу раздела волны, можно

записать соотношения Френеля в данном примере границы раздела диэлектрических сред:

2 q 2

q 2

p 1

(13)

q 2 p 1

ref

q 2

p 1

Коэффициент отражения может быть определен как

E ref

(14)

R |

Надо помнить, что знак параметра p не определен, так что ожидать сингулярность в (13) или в (14) нет оснований.

Вернувшись к выражениям для напряженностей электрических и магнитных

полей при x 0 :

E y(1)

Ein

exp(

i t iqx i z ) E ref exp(

i t iqx i z ) c.c. ,

(18.1)

(1)

exp( i t iqx i z ) E

exp( i t iqx i z ) c.c. ,

(18.2)

ref

H (1)

exp( i t iqx i z ) E

exp( i t iqx i z ) c.c. ,

(18.3)

ref

и при x 0

( 2 ) E

exp( i t ipx i z ) c.c. ,

(18.4)

H ( 2 )		cp	E			exp( i t ipx i z ) c.c. ,		(18.5)
					tr

z	2
	2
H ( 2 )		c		E			exp( i t ipx i z ) c.c. ,	(18.6)
H ( 2 )				E		tr	exp( i t ipx i z ) c.c. ,	(18.6)
x						tr
			2

Чтобы определить направление распространения энергия волны, следует рассмотреть вектор Пойнтинга

S4 (E H )

иусреднить его по быстро меняющимся колебаниям электромагнитного поля. В рассматриваемом случае ТЕ-волн имеем

S x (c / 4 ) E y H z ,

S z (c / 4 ) E y H x .

Используя выражения (18), после усреднения по быстрым пространственным колебаниям можно найти следующие выражения

при x 0 : S

qc 2

| E

c 2

| E

|2 | E

(20.1)

ref

при x 0 : S

pc 2

| E

, S

c 2

| E

|2 .

(20.2)

Выражения (20.1) показывают, что вектор Пойнтинга при

x 0

складывается из двух

векторов, отвечающих падающей и отраженной волне. При x 0 , поскольку там 2 0 , z-компонента вектора Пойнтинга оказывается отрицательной. Так как принято, что

энергия распространяется вдоль оси Х в положительном направлении, то S x				должна
быть положительной. Следовательно, надо выбрать p 0 .
Соотношения (10) можно переписать как
q 2 2 ( / c ) 2 n 2 ,	p 2 2	( / c ) 2 n 2	,	(10*)
1		2

так, что полученные здесь компоненты волновых векторов можно параметризовать углами падения и преломления

( / c )n1 sin	in	( / c )n2 sin tr	,	(15.1)
q ( / c )n1 cos in	,	p ( / c )n2 cos tr .		(15.2)
Поскольку p 0 следует в (15.2) считать		n2 0 . Таким	образом,	отрицательный

показатель преломления является следствием предположения о направлении переноса энергии преломленной волной. Параметр должно быть положительным, поскольку в

правой части (15.1) стоит положительная величина. Следовательно, формула Снеллиуса принимает следующий вид

n1 sin in | n2 | sin( tr ) . (16)

Это означает, что преломленный луч лежит в той же плоскости, что и падающий

(Рис.1).

Используя параметризацию (15) можно переписать соотношения Френеля как

n1 2

cos in

n2 1

cos tr

| 2

| cos in | n2

| 1

cos tr

(17.1)

ref

n1 2

cos in

n2 1

cos tr

| 2

| cos in | n2

| 1

cos tr

E tr

2 n1 2

cos in

E in

2 n1 | 2 | cos in

E in .

(17.2)

| 2

| cos in | n2

| 1

n1 2 cos in n2 1 cos tr

cos tr

Отсюда видно, что направление векторов напряженности электрического поля не меняется при прохождении границы раздела и отражении от оной. Но поскольку выражения для магнитных полей (7) содержат как коэффициент магнитную проницаемость, знаки компонент вектора напряженности магнитного поля преломленной волны меняется на противоположный. Направление распространения, вектора напряженности электрического и магнитного полей теперь образуют ''левую тройку ортогональных векторов'', что послужило основанием называть такую среду

средой левой руки, левыми средами (Left handed material). Или средами с отрицательным преломлением.

				X
		Etr
Рис. 1		Str		Vtr
				Vtr
Ход лучей при преломлении,
направление фазовых
скоростей и векторы				Vref	Z
Пойнтинга по разные стороны		Sin		Vref	Z
Пойнтинга по разные стороны		Sin			ErefE
границы раздела.	Ein	V	in	Sref	ErefE
	Ein		in	Sref	ref

Можно найти выражения для фазовых скоростей. Рассматривается падающая волна. Уравнение поверхности постоянных фаз при x 0 есть

t qx z const ,

Что в терминах проекций фазовой скорости смотрится как

	q
t		x	z	t

x	z	const

v x
	v z

Для отраженной волны аналогично получается

q
	x	z	t

x	z	const

v x
	v z

<<< < Предыдущая 1 2 3 4 5 67 / 107 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
03.06.2015933.51 Кб9Лекции - Раздел 1.pdf
#
01.03.2025208.38 Кб0Лекции ОИ.doc
#
01.05.20251.12 Mб0Лекции по окр. миру.doc
#
03.06.201514.11 Mб13Лекции по физкинетике.PDF
#
03.06.2015386.05 Кб39Лекции по философии (Семенов) 2006-2007.doc
#
03.06.20151.71 Mб21Лекции.pdf
#
03.06.201583.97 Кб42Лекция Потребности и мотивы.doc
#
03.06.20151.29 Mб29Лекция 1 - конспект.pdf
#
03.06.20151.87 Mб58Лекция 10 - Неметаллические материалы.pdf
#
03.06.2015910.58 Кб8Лекция 10.pdf
#
03.06.20152.45 Mб48Лекция 12 - Наноматериалы и УНТ.pdf