Файловый архив студентов. Файловый архив студентов.
1304 вуза, 5161 предмета.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Московский государственный физико-технический университет (МФТИ)
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

МФТИ 2012 Умнов АЕ АГ+ЛА Стр001-544

.pdf
Скачиваний:
42
Добавлен:
03.06.2015
Размер:
6.64 Mб
Скачать
☆

 

Прил. 1 . Свойства линий второго порядка на плоскости

459

 

 

 

Приложение 1.4. Парабола и ее свойства

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Определение

Линия, уравнение которой в некоторой ортонорми-

 

 

 

Прил. 1.4.1.

рованной системе координат имеет вид

 

 

 

 

 

 

 

 

 

 

 

y 2 = 2 px ; p > 0 ,

 

 

 

 

 

называется параболой.

 

 

 

 

 

 

 

p

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Определение

Точка

 

2

 

 

называется фокусом параболы.

 

 

 

 

Прил. 1.4.2.

 

0

 

 

 

 

 

 

 

 

 

 

 

 

p

 

 

 

 

 

 

Прямая

 

x = −

называется директрисой парабо-

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

лы.

 

 

 

 

 

 

 

 

 

 

 

 

Число

p называется фокальным параметром пара-

 

 

 

 

болы.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Свойства параболы иллюстрирует рис. Прил. 1.4.1, на котором че- рез α обозначим угол между касательной и фокальным радиусом, а

через b – угол между касательной и положительным направлением

оси абсцисс.

Свойства параболы

1°. Парабола – неограниченная кривая, существующая "x³ 0;

2°. Парабола L обладает осевой симметрией относительно оси Ox , что вытекает из отношения

x

L

x

L,

y

 

− y

 

очевидного для канонического уравнения параболы.

460

Аналитическая геометрия и линейная алгебра

Рис. Прил. 1.4.1

3°. Для параболы имеет место монотонное возрастание абсо- лютной величины ординаты при возрастании абсциссы, причем в нуле касательная к параболе вертикальна.

Теорема

Пусть A =

x

есть точка, принадлежащая пара-

Прил. 1.4.1.

 

y

 

боле L , заданной каноническим уравнением, тогда имеют место следующие соотношения:

1°.

2°.

3°.

r = x + p ;

2

ρ( A, F ) =

1;

ρ( A, D)

ρ(M , F ) = 1 M , M L ; ρ(M , D)

→

5°. Ða = Ðb .

4°. | FB | = p ;

 

Прил. 1 . Свойства линий второго порядка на плоскости

461

 

Доказательство.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1°.

Имеем r =

(x -

 

p

)2 + y 2 , используя каноническое

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

уравнение, получаем

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

r = x 2 - px +

p 2

 

 

+ 2 px = | x +

p

| ,

 

 

 

 

 

 

 

 

 

 

 

 

4

 

2

 

 

 

 

но поскольку

x ³ -

p

,

приходим сразу к справедли-

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

вости утверждений 1° и 2°.

 

 

Справедливость 3° докажите самостоятельно.

 

 

 

 

→

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4°.

 

 

 

 

 

 

 

 

p

 

 

 

 

 

 

 

Наконец, |FB |= 2 p

 

= p.

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

5°. Доказательство приводится после доказательства тео- ремы Прил. 1.4.2.

Теорема доказана.

Замечания о свойствах параболы

Каноническое уравнение параболы вида y = ax 2 , изучаемой в

курсе элементарной математики, получается путем взаимного пере- именования координатных переменных.

Из теоремы Прил. 1.4.1 следует возможность альтернативных формулировок свойств параболы.

Директориальное свойство параболы: парабола есть геометри-

ческое место точек, отношение расстояния от которых до дан- ной точки (фокуса) к расстоянию до данной прямой (директри- сы) постоянно и равно единице.

462 Аналитическая геометрия и линейная алгебра

Оптическое свойство параболы: касательная в любой точке гиперболы образует равные углы с фокальным радиусом точки касания и положительным направлением оси абсцисс. (Каждый луч света, выходящий из фокуса параболы, после отражения от параболы распространяется параллельно ее оси.)

Проведение касательных к параболе

Теорема

Прил.1.4.2

.

Пусть A =

x0

есть точка, принадлежащая пара-

y0

 

 

боле, заданной каноническим уравнением, тогда уравнение касательной к этой параболе, проходящей через точку A , имеет вид

yy0 = p(x + x0 ) .

Доказательство.

Уравнение касательной в точке A имеет вид

 

 

 

′

 

y - y0 = y (x0 )(x - x0 ) .

Для параболы из канонического уравнения получаем

2 yy′ = 2 p , то есть

y¢(x0 ) =

p

, y0 ¹ 0 .

y0

 

 

 

 

 

Но тогда y - y0 =

 

p

(x - x0 ) , и принимая во внимание,

 

 

 

 

y0

 

что y02 = 2 px0 , окончательно получим

 

 

yy0 = p(x + x0 ) .

Наконец, непосредственно проверяем утверждение теоремы для точки y0 = 0 , где уравнение касательной x = 0 .

Теорема доказана.

 

 

Прил. 1 . Свойства линий второго порядка на плоскости

463

 

 

 

Доказательство свойства 5° теоремы Прил.1.4.1.

 

 

 

A есть

 

 

 

 

 

 

 

 

 

Направляющий вектор касательной к параболе в точке

 

 

 

 

y0

 

 

 

, а вектор фокального радиуса –

 

x0 −

p

 

 

. Поэтому

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

p

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y0 (x0

−

p

) + py0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y0

 

 

 

 

 

 

 

 

 

 

 

cos α =

 

 

 

 

2

 

 

 

 

 

=

 

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

p

 

 

 

 

 

 

 

 

y02 + p 2

 

 

 

2

 

2

 

 

 

 

 

 

2

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y0

+ p

 

 

 

(x0 −

2

)

 

+ y0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Но, с другой стороны, косинус угла β между векторами

 

y0

 

 

 

и

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

p

 

 

 

 

1

0

выражается той же формулой. Поскольку углы α и β

острые, то они равны.

Теорема доказана.

Уравнение параболы в полярной системе координат

Поместим полюс полярной системы координат в фокус параболы, а полярную ось на- правим по линии, перпендику- лярной директрисе и проходя- щей через ее фокус (рис. Прил. 1.4.2). Для произвольной точки A , лежащей на параболе,

ρ = x + p =

Рис. Прил.1.4.2

2

464 Аналитическая геометрия и линейная алгебра

= p + ρ cos α + p = p + ρ cos ϕ .

2 2

Откуда ρ(1 − cos ϕ) = p и окончательно

ρ =

p

 

.

1 −cos ϕ

(Сравните эти формулы с выкладками в § 4.6.)

Прил. 2 . Свойства поверхностей второго порядка

465

Приложение 2

СВОЙСТВА ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА

В теореме 4.5.1 были перечислены конкретные типы поверхностей второго порядка, различие между которыми сохраняется при переходе из одной декартовой системы координат в другую. В данном прило- жении будут рассмотрены основные свойства поверхностей этих ти- пов.

Приложение 2.1. Вырожденные поверхности второго порядка

К вырожденным поверхностям второго порядка относятся типы, указанные в первой части таблицы формулировки теоремы 4.5.1.

В первых двух столбцах этой таблицы перечислены типы пустых множеств, а также объекты точечно-линейного типа, исследование которых полностью аналогично случаям, рассмотренным в приложе- нии 1, в ортонормированной, канонической системе координат

→→ →

{O, e1 , e2 , e3 } .

Первые три типа поверхностей, содержащиеся в третьей колонке таблицы, являются частными случаями цилиндрической поверхности,

x = 0,

образующая которых параллельна прямой а направляющими

y = 0,

служат плоские кривые – эллипс, гипербола и парабола, соответст- венно расположенные в плоскости Oxy .

466

Аналитическая геометрия и линейная алгебра

Описание свойств невырожденных поверхностей второго порядка будет также выполнено в ортонормированной системе координат

→→ →

{O, e1 , e2 , e3 } .

В общем случае можно показать, что в сечении поверхности вто- рого порядка плоскостью получается кривая второго порядка. Однако для описания основных свойств невырожденных поверхностей второ- го порядка достаточно рассмотреть сечения, параллельные коорди- натным плоскостям.

Приложение 2.2. Эллипсоид

Определение

Поверхность, задаваемая в некоторой ортонормиро-

Прил. 2.2.1.

ванной системе координат уравнением вида

x 2

+

y 2

+

z 2

= 1 , a > 0, b > 0, c > 0,

a 2

b2

c 2

 

 

 

называется эллипсоидом.

Свойства эллипсоида

1°. Эллипсоид – ограниченная поверхность, поскольку из его кано- нического уравнения следует, что | x |≤ a ; | y |≤ b ; | z |≤ c .

2°. Эллипсоид обладает:

-центральной симметрией относительно начала коорди- нат;

-осевой симметрией относительно координатных осей;

-плоскостной симметрией относительно координатных плоскостей.

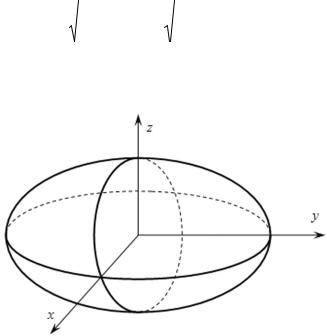
3°. В сечении эллипсоида плоскостью, ортогональной любой из осей координат, получается эллипс. Например, рассматривая секущую

Прил. 2 . Свойства поверхностей второго порядка

467

плоскость z = z0 ,

где

 

 

z0

 

 

< c , получаем следующее уравнение

 

 

 

линии сечения:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x 2

 

 

 

 

 

 

+

 

y 2

 

 

= 1,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

z

2

 

 

 

 

 

2

 

 

 

 

 

(a 1

−

0

 

) 2

 

 

 

(b 1 −

z0

) 2

 

 

c 2

 

 

 

c 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

z = z0 ,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

являющейся эллипсом. (Рис. Прил. 2.2.1.)

Рис. Прил. 2.2.1

Приложение 2.3. Эллиптический параболоид

Определение

Поверхность, задаваемая в некоторой ортонормиро-

Прил. 2.3.1.

ванной системе координат уравнением вида

 

 

468 Аналитическая геометрия и линейная алгебра

 

 

 

x 2

+

y 2

= 2z , a > 0, b > 0,

 

 

 

 

a 2

b2

 

 

 

 

 

называется эллиптическим параболоидом.

Свойства эллиптического параболоида

1°. Эллиптический параболоид – неограниченная поверхность, по- скольку из его канонического уравнения следует, что z ³ 0 и

принимает сколь угодно большие значения.

Рис. Прил. 2.3.1

2°. Эллиптический параболоид обладает

-осевой симметрией относительно оси Oz ;

-плоскостной симметрией относительно координатных плоскостей Oxz и Oyz .

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности