
2012-2013 уч. год, № 2, 9 кл. Физика. Кинематика
мощью теоремы Пифагора: v = |
vx |
2 + vy |
2 . В соответствии с системой |
|||
уравнений |
(19) в этот |
момент (при |
t =τ ) имеем: vx = v0 cosα, |
|||
vy = v0sinα − gτ = −v0sinα. |
Следовательно, |
|||||
v = v |
2cos2α + v 2sin2α = v |
0 |
(так как cos2 α +sin2 α =1 ). |
|||
0 |
0 |
|
|
|
|
|
Направление скорости тела в момент падения составляет угол α с направлением оси Ox. Этот угол отсчитывается по часовой стрелке от направления оси Ox.
Пусть при t =τ1 |
тело достигло максимальной |
высоты. |
В этот |
мо- |
|||||
мент vy =0, y = H. |
Соответствующие уравнения систем (19) и (20) |
||||||||
дают: |
|
|
|
|
gτ12 |
|
|
||
0 = v0 sinα − gτ1 , H =(v0 sinα)τ1 − |
|
|
|||||||
|
2 |
. |
|
|
|||||
Отсюда последовательно находим: τ1 = |
v |
0 |
sinα |
, H = |
v 2 sin2 α |
. |
|||
|
|
|
0 |
||||||
|
|
g |
|
2g |
|||||
|
|
|
|
|
|
|
|
||
Видим, что τ = 2τ1.
Уравнение траектории получим, исключив из системы (20) время t :
y(x) = − |
|
g |
x2 + tgα x. График траектории тела представляет |
|
2v0 |
2 cos2 α |
|||
|
|
собой участок параболы, ветви которой направлены вниз.
§7. Примеры решения задач
Задача 1. Два маленьких стальных шарика брошены одновременно из одной и той же точки с поверхности земли с начальными скоростями
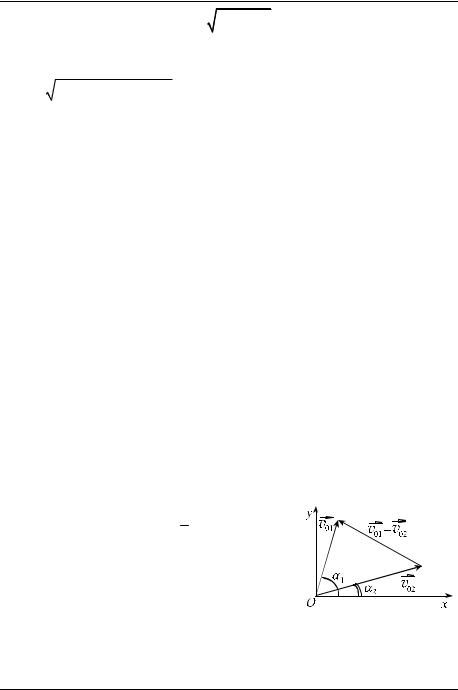
v01 =5 м/c и v02 =8 м/c, направленными под углами α1 =80o и α2 = 20o к горизонту соответственно. Чему равно расстояние между
шариками, спустя время t = 13 c после броска?
Траектории шариков лежат в одной вертикальной плоскости. Сопротивлением воздуха
пренебречь. Решение. Шарики движутся в поле тя-
жести Земли с постоянным ускорением |
g |
(сопротивлением воздуха пренебрегаем). |
Рис. 20 |
Выберем систему координат так, как показано на рис. 20, начало отсчёта поместим в точку бросания. Для радиус-векторов шариков r1 (t) и
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
21

2012-2013 уч. год, № 2, 9 кл. Физика. Кинематика
r |
|
r |
|
|
r |
|
|
r |
|
|
|
r |
|
|
|
|
|
r |
|
r |
|
|
r |
|
|
|
r |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
gt2 |
|
|
|
|
|
|
|
|
|
|
|
gt |
2 |
|
||||||||||||||||||
r (t) имеем: |
|
r (t) = r |
|
+ v |
+ |
|
|
, |
|
|
|
r (t) |
= r |
+ v |
02 |
+ |
|
|
|
. |
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
2 |
|
|
1 |
|
|
01 |
|
01 |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
02 |
|
|
|
|
|
2 |
|
|
|
||||||||
Искомое |
|
расстояние l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
равно модулю |
|
|
разности радиус-векторов |
|||||||||||||||||||||||||||||||||||
шариков в |
момент времени t = |
|
1 |
|
c. Так как шарики были брошены из |
|||||||||||||||||||||||||||||||||||
3 |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
одной и той же точки, то r01 = r02 , следовательно: |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
l = |
|
|
rr1(t) −rr2(t) |
|
= |
|
vr01−vr02 |
|
t. |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
(Остальные слагаемые при вычитании радиус-векторов уничтожились.) |
||||||||||||||||||||||||||||||||||||||||
В свою очередь по теореме косинусов (см. рис. 20): |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
vr |
|
−vr |
|
= |
|
|
|
v |
2 |
+ v |
2 |
−2v |
01 |
v |
02 |
cos(α |
1 |
−α |
2 |
). |
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
01 |
|
02 |
|
|
01 |
|
|
02 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Подставляя |
в это |
равенство числовые значения входящих в него ве- |
||||||||||||||||||||||||||||||||||||||
личин, получим |
|
vr01 −vr02 |
|
|
|
=7 м/c. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Тогда искомое |
|
расстояние между |
шариками |
|
в |
|
|
момент времени |
||||||||||||||||||||||||||||||||
t = |
1 |
c будет равно l =7 |
|
м |
|
|
1 |
c = |
7 |
м ≈ 2,3м. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
c |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Задача 2. |
Два тела брошены вертикально вверх с поверхности |
|||||||||||||||||||||||||||||||||||||||
земли из одной точки вслед друг за другомr с интервалом времени τ, с одинаковыми начальными скоростями v0 . Пренебрегая сопротивлением воздуха, определить через сколько времени они «встретятся»? Про-
комментируйте решение для v0 < g τ2 .
Решение. Направим ось Oy вертикально вверх, начало отсчёта по-
местим в точку бросания. Отсчёт времени будем вести, начиная с момента бросания первого тела. Начальные условия движения тел:
1) t0 =0, y01 =0, vy01 = v0 ; 2) t0 =τ, y02 =0, vy02 = v0 . Проекции ускорений тел при отсутствии сопротивления воздуха равны: ay1= ay 2 = −g. Урав-
нения движения тел в проекциях на ось Oy с учётом начальных условий имеют вид:
y1 (t) = v0t − gt22 , y2 (t) = v0 (t −τ) − g(t −2 τ)2 . (Заметим, что y2 =0 при 0 <t ≤τ. )
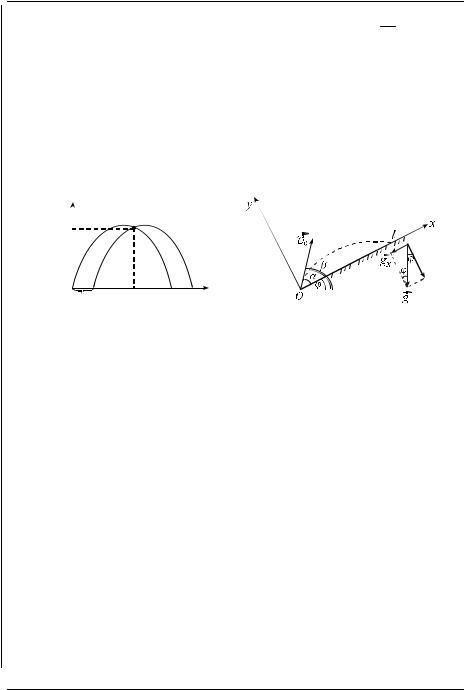
Для наглядности изобразим графики этих функций на одном чертеже (рис. 21). Из чертежа видно, что «встреча» произойдёт в некоторый
момент времени tx в точке A, |
где пересекаются графики y1(t) и |
|||||||
y2 (t). Таким образом, условие «встречи»: |
|
y1 (tx ) = y2 (tx ), то есть |
||||||
v0tx − |
gt |
2 |
= v0 (tx |
−τ) − |
g(t |
x |
−τ)2 |
. |
2 |
|
|
|
2 |
||||
|
|
|
|
|
|
|
||
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
22
2012-2013 уч. год, № 2, 9 кл. Физика. Кинематика
Решая это уравнение относительно tx , находим: tx = vg0 +τ2 . Про-
анализируем полученное выражение при v0 < gτ / 2. Известно (см.
Пример 7), что время полёта тела, брошенного вертикально, равно
2v0 / g. Поэтому, если v0 < gτ / 2, то τ > 2v0 / g. Это означает, что сна-
чала упадёт на землю первое тело, а только затем будет брошено вверх второе. Иными словами, тела «встретятся» в точке бросания.
y |
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
y (t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y1(t) |
|
y2(t) |
|
|
|
|
|||
|
|
|
|
|
||||||||
O |
|
τ |
zx |
2 v0 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
Рис. 21 |
|
|
|
|
Рис. 22 |
||||
Задача 3. Мальчик, находясь на плоском склоне горы с углом наклона ϕ =30o , бросает камень в сторону подъёма горы, сообщив ему
начальную скорость v0 , направленную под углом β =60o к горизон-
ту. На каком расстоянии от мальчика упадёт камень? Сопротивлением воздуха пренебречь.
Решение. Выберем систему отсчёта так, как показано на рис. 22, поместив начало отсчёта O в точку бросания. В этой системе отсчё-
та начальная скорость камня составляет с осью Ox угол α =β −ϕ =30o. Начальные условия: x0 =0, y0 =0, v0x = v0 cosα, v0y = v0 sinα. Проекции ускорения камня в отсутствие сопротивления воздуха равны (см. рис. 22): ax = −g sinϕ, ay = −g cosϕ. Здесь мы учли, что угол между
вектором g и перпендикуляром к поверхности горы равен углу наклона горы ϕ =30o (почему?), кроме того, по условию задачиϕ =α.
Запишем уравнения системы (14) с учётом начальных условий:
x(t) =(v0 |
cosα)t −(g sinϕ) |
t2 |
, |
y(t) =(v0 sinα)t −(g cosϕ) |
t2 |
. |
|
|
|||||
|
2 |
|
2 |
|
||
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
23
2012-2013 уч. год, № 2, 9 кл. Физика. Кинематика |
|
|
|
||||
|
Время полёта τ камня найдём из последнего уравнения, зная, что |
||||||
|
|
y(τ) =0, cosϕ = |
3 , |
sinα = 1 . |
|
||
|
|
|
|
2 |
2 |
|
|
А именно τ = 2 v0 . (Значение τ =0 мы отбросили, т. к. оно не связа- |
|||||||
|
|
3 g |
|
|
|
|
|
но с вопросом задачи). |
|
в уравнение для x(t), |
|
||||
|
Подставляя найденное значение τ |
определим |
|||||
искомое расстояние (иными словами, дальность полёта): |
|
||||||
|
|
|
l = x(τ) = |
2 v 2 |
. |
|
|
|
|
|
0 |
|
|||
|
|
|
|
3 g |
|
|
|
uur |
Задача 4. Массивная платформа движется с постоянной скоростью |
||||||
V0 |
по горизонтальному полу. С заднего края платформы производится |
||||||
удар по мячу. Модуль начальной скорости мяча относительно плат- |
|||||||
формы равен u = 2V , причём вектор |
u составляет угол α =60o с гори- |
||||||
|
|
0 |
|
|
|
|
|
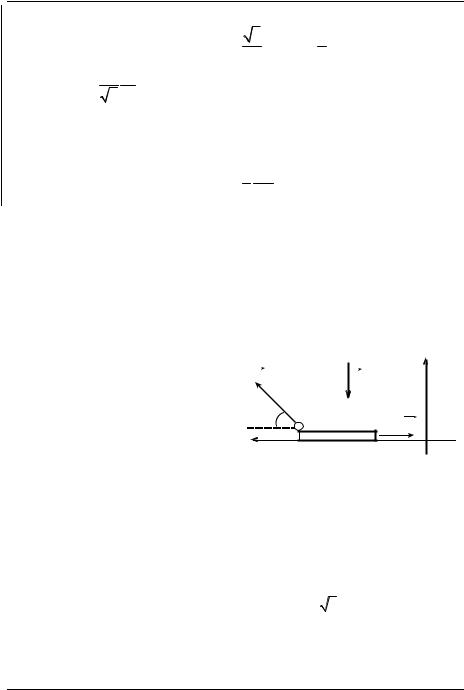
зонтом (рис. 23). На какую максимальную высоту над полом поднимет- |
|||||||
ся мяч? На каком расстоянии от края платформы будет находиться мяч |
|||||||
в момент приземления. Высотой платформы и сопротивлением воздуха |
|||||||
пренебречь. Все скорости лежат в |
|
|
y |
||||
одной |
вертикальной |
плоскости. |
u |
g |
|||
|
|||||||
(ФЗФТШ при МФТИ, 2009.) |
|
|
|
||||
|
Решение. Для описания движе- |
α |
|
||||
ния мяча и платформы введём сис- |
V0 |
||||||
тему отсчёта, связанную с полом. |
|
|
|||||
/ / / / / / / / / / / / / / / / / / / / / |
|||||||
Ось Ox направим горизонтально в |
x |
|
O |
||||
направлении удара, а ось Oy − вер- |
|
Рис. 23 |
|
||||
тикально вверх (рис. 23). |
|
|
|
|
|||
Движение мяча происходит с постоянным ускорением a, причём ax = 0, ay = −g, где g − величина ускорения свободного падения.
Проекции начальной скорости v0 мяча на оси Ox и Oy равны: v0,x =V0,x +ux = −V0 +2V0 cos60o = −V0 +V0 =0,
v |
=V |
+u |
y |
=0 + 2V sin 60o = |
3V . |
0,y |
0, y |
|
0 |
0 |
Равенство нулю горизонтальной скорости мяча означает, что его движение происходит только по вертикали, и он упадёт в точке удара.
Максимальную высоту подъёма (ymax ) и время полёта мяча найдём
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
24
