Vse_bomby_s_dokazatelstvami

7. Теорема о равномерной непрерывности функции непр на компакте. Теорема (Кантор). Пусть - компакт , и функция f непрерывна на E. Тогда f равномерно непрервына на E.

Доказательство. Предположим, что теорема не верна, т.е. что существует функция f, непрерывная, но не равномерно непрерывная на E. Тогда .

Будем брать в качестве и соответствующую пару точек x,yобозначать через x(m),y(m).Тогда имеем

,

Выделим из последовательности{x(m)}сходящуюся подпоследовательность , , что возможно в силу ограниченности {x(m)} по теореме

Больцано-Вейерштрасса. Тогда из следует,

что . Точка , так как Eзамкнуто. В силу непрерывности f в точке x(0) по множеству E имеем при а это противоречит тому, что Теорема доказана

8. Достаточные условия дифференцируемости функции нескольких переменных.

Теорема. Пусть в точке x(0) непрерывны все частные производные

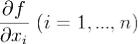функции f. Тогда f дифференцируема в точке x(0). Доказательство ради простоты записи проведем для случая функции двух переменных (n = 2). Непревность частных производных функции в

точке 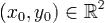включает предположение об их существовании в некоторой окрестности Uδ((x0,y0)).

Считая (Δx)2 + (Δy)2 < δ2, рассмотрим приращение функции

. Правая часть представляет собой сумму приращений функции по одной переменной при фиксированной другой. Применяя по соответствующей переменной теорему Лагранжа о конечных приращениях, имеем

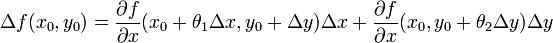. Но производные непрерывны в точке (x0,y0). Поэтому

где при . Подставляя полученные выражения в Δf(x0,y0) имеем

.

Справедливо

Следовательно функция f дифференцируема в точке (x0,y0).

9. Теорема о неявной функции нескольких переменных.

Пусть функция F двух переменных удовлетворяет следующим условиям: 1. F непрерывна в некоторой окрестности U(x0,y0) точки (x0,y0);

2 F(x0,y0) = 0;3 , F'y непрерывна в точке (x0,y0). Тогда существует прямоугольная окрестность точки

такая, что на ней,где функциянепрервна на Qδ(x0),f(x0) = y0.

10. Экстремумы функций нескольких переменных. Необходимые условия, достаточные условия.

Определение. Пусть функция f определена на некоторой окрестности точки x(0). Точка x(0) называется точкой минимума функции f, если

Необходимые условия экстремума. Пусть функция f имеет в точке

экстремума x(0) частную производную. Тогда . Доказательство. Пусть для определенности i = 1. Рассмотрим функцию

одной переменной x1 . Она имеет экстремум в точке . Тогда по теореме Ферма

.

Определение. Точка x(0) называется стационарной точкой функции f, если f дифференцируема в точкеx(0) и .

Лемма: Пусть квадратичная форма 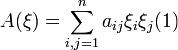положительно определенна. Тогда при некотором μ > 0

Доказательство. При | ξ | = 0 (2) - очевидно. При | ξ | > 0, деля обе части (2)

на | ξ | 2 и пологая , сводим доказательство (2) к доказательству неравенства

Последнее вытекает из теоремы Вейерштрасса, утверждающей, что непрерывная функция (A(η)) на компакте достигает своего наименьшего значения в некоторой точке η *

Достаточные условия строгого экстремума. Пусть функция f дважды непрерывно дифференцируема в некоторой окрестности стационарной точки .

Пусть второй дифференциал d2f(x(0)) функции f в точке x(0)

является положительно определенной (отрицательно) квадратичной формой. Тогда x(0) - точка строгого минимума (максимума) функции f. Если же квадратичная форма d2f(x(0)) является неопределенной, то в точке x(0) нет экстремума.

Доказательство.Напишем разложение функции f по формуле Тейлора в окрестности стационарной точки x(0) с остаточным членом в форме Пеано:

Члены с первыми производными отсутствуют, так как x(0) - стационарная точка. Запишем последнюю формулу в виде

Пусть сначала d2f(x(0)) (3) - положительно определенная форма. Тогда из (4)

и (2) следует, что Поскольку, то

Последнее значит, что x(0) - точка строгого минимума функции f. Аналогично для отрицательно определенной формы.

Пусть теперь d2f(x(0)) (3) - неопределенная квадратичная форма.

Значит такие, что A(ξ') < 0,A(ξ'') > 0. Полагая 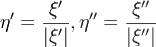, получаем, чтоα = A(η') < 0,β = A(η'') > 0, | η' | = 1 | η'' | = 1

Пусть . Тогда из (4)

при всех достаточно малых . Если же взять , то

Видно, что при любой сколь угодно малой

окрестности U(x(0)) разность , принимает как отрицательные, так и положительные значения. Следовательно, точка x(0) не является точкой экстремума функции f.

11. Свойства интеграла с переменным верхним пределом (непрерывность, дифференцируемость). Формула Ньютона-Лейбница.

Пусть f интегрируема на [a,b]. Тогда на [a,b] определена функция

называемя интегралом с переменным верхним пределом.

Теорема 1. Пусть f интегрируема на [a,b]. Тогда F непрерывна на [a,b].

Доказательство. Пусть . Тогда

Функция f ограничена на [a,b] (поскольку она интегрируема), так что при некотором M будет .Следовательно при ,что и требовалось показать. Теорема 2. Пусть функция f интегрируема на [a,b] и непрерывна в

точке . Тогда функция F(x)имеет производную в точке x0 и

Доказательство. Вычитая из предпологаемый предел f(x0), имеем при

.

Пусть . Тогда в силу непревности f в точке , если .

Следовательно, при | Δx | < δ (и )

Но это означает, что при , чтд. Теорема 3.Пусть функция f непрерывна на (a,b). Тогда она имеет

на (a,b) первообразную, где .

Доказательство.следует из формулы (2) при 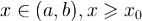, и формулы (3) при , если учесть, что в последнем случае F можно

представить в виде .

Основная теорема интегрального исчисления. Пусть функцияfнепрерывнана отрезке [a,b] и Φ - её первообразная на этом

отрезке. Тогда.Это называется формулой НьютонаЛейбница.

Доказательство. Функция является первоообразной для функции f на отрезке[a,b]. Поэтому,т.е.

.

Отсюда следует при x = a получаем 0 = Φ(a) + C. Выражая из последнего равентсва C и подставляя его в предшевствующееравентсво получаем, что

. - при x = b совпадает с (4).

12. Равномернаясх-сть функциональных последовательностей и рядов. Определение. Говорят, что функциональная последовательность сходится на множестве E равномерно к

функции , если при

При этом пишут.

Критерий Коши равномерной сходимости последовательности.Последовательность , сходится на E равномерно тогда и только тогда, когда выполняется условие Коши:

. Доказательство.Необходимость. Пусть . Тогда

при Отсюда следует, что ,

Достаточность. Пусть выполнено условие Коши. Тогда при каждом фиксированном выполнено условие

В силу критерия Коши сходимости числовой последовательности{fn(x)} сходится для . Обозначим предел

числовой последовательности{fn(x)}через f(x). Покажем, что . Перейдем для этого в оценке (2) к пределу при . Получим, что .Переходя в последнем

неравенстве к верхней грани по , видим что по опр 2. Определение. Говорят, что ряд сходится на E равномерно, если последовательность {Sn} его частичных сумм сходится на E равномерно.

Непрерывность, интегрируемость и дифференцируемость суммы равномерно сходящегося ряда.

Непрерывность. Пусть . Если все функции fn непрерывны в точке x(0) по множеству E, то и предельная функция f непрерывна в точке x0 по множеству E.

Доказательство. Пусть . Тогда.

Тогда при

.

В силу непревности функции 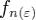в точке x(0) по множеству E

. Отсюда и из предыдущего неравенства следует, что

Следовательно, функция f непрерывна в точке x(0) по множеству E.

Для рядов достаточно положить . Интегрируемость. Пусть функции fn непрерывны на отрезке при

всех и при .Тогда при . Доказательство. Функция f(x) по теореме 1 непрерывна на отрезке [a,b] при всех и, следовательно интегрируема на [a,b]. Пусть . Тогда в силу равномерной сходимости {fn} к функции f .

Следовательно для всех

откуда и следует утверждение теоремы.

Для рядов достаточно положить . Дифференцируемость. Пусть последовательность {fn} непрерывно дифференцируемых на отрезке [a,b]функций сходится в точке 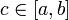, а, последовательность производных {f'n} равномерно сходится на[a,b] к некоторой функции φ. Тогда последовательность {fn} равномерно сходится на [a,b] к некоторой функции непрерывно дифференцируемой

на [a,b] функции f и f' = φ, так что на [a,b]. Доказательство. По теореме 1 функция φ непрерывна на [a,b]. В силу теоремы 2 и формулы Ньютона-Лейбница получаем, что

.

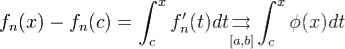Числовую сходящуюся последовтельность {fn(c)} можно считать, очевидно, функциональной последовательностью, равномерно сходящейся на [a,b]. Тогда последовательность {fn} равномерно сходиться на [a,b] к некоторой функции f.Переходя в левой части последней формулы к пределу

при , получаем, что.

Правая часть этого равенства является дифференцируемой функцией. Следовательно таковой является и левая часть, а значит и функция f. Дифференцируя равенство получаем, что 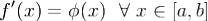. Теорема

доказана.Для рядов достаточно положить .