Vse_bilety_BEZ_dokazatelstv
.pdf1. Теорема Больцано-Вейрштрасса.
Из любой огрпосл-сти можно выделить сх-сяподпоследовательность.
Критерий Коши сходимости числовой последовательности.
Для того чтобы последовательность имела конечный предел, необходимо и достаточно, чтобы она былафундаментальной .
2.Теорема Вейерштрасса. Функция, непрерывная на отрезке, ограничена и достигает своих верхней и нижней граней.
3.Теорема о промежуточных значениях непрерывной функции.Пусть функция непрерывна на отрезке [a,b], f(a) = A, f(b) = B. Пусть C находится между A и B.Тогда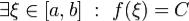
4.Теорема Ролля.Пусть функция f:
1. непрерывна на [a,b];2. дифференцируема на (a,b);3. f(a) = f(b). Тогда 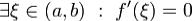 .
.
Теорема Лагранжа.Если функция f(x) непрерывна на отрезке [a,b] и дифференцируема на интервале (a,b), то в этом интервале найдется хотя бы одна точка ξ: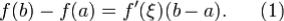
Теорема Коши.Если функции f(x) и g(x) непревны на отрезке [a,b], дифференцируемы на интервале (a,b), причем 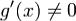 во всех точках этого
во всех точках этого
интервала, то найдется хотя бы одна точка 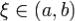 :
: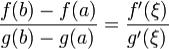 .
.
5. Остаточный член формулы Тейлора.
Пусть 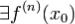 . Тогда в некоторой окрестности U(x0) можно написать
. Тогда в некоторой окрестности U(x0) можно написать
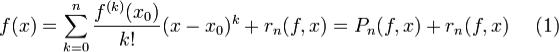 ,
,
которое называется формулой Тейлора функции f в точке x0,
где Pn(f,x) называется многочленом Тейлора, аrn(f,x) - остаточным членом Тейлора (после n-го члена).
Если существует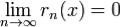 ,то согласно определению сходимости ряда (1) сходится к функции f(x) в точке x.
,то согласно определению сходимости ряда (1) сходится к функции f(x) в точке x.
ЛеммаПусть 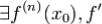 в
в 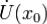 . Тогда в
. Тогда в 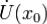 верно
верно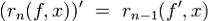
Теорема. Формула с остаточным членом в форме Лагранжа.
Пусть x > x0(x < x0), 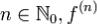 непрерывна на отрезке [x0,x]([x,x0]),
непрерывна на отрезке [x0,x]([x,x0]), 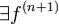 на интервале (x0,x)((x,x0)). Тогда справедлива формула (1), в которой
на интервале (x0,x)((x,x0)). Тогда справедлива формула (1), в которой
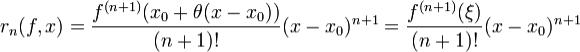 , 0 < θ < 1.
, 0 < θ < 1.
Теорема. Формула Тейлора с остаточным членом в форме Пеано.
Пусть 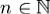 и
и 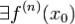 . Тогда справедлива формула (1), в которой
. Тогда справедлива формула (1), в которой 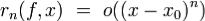 при
при 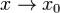 .
.
6. Исследование функций одной переменной при помощи первой и второй производных на монотонность, локальные экстремумы, выпуклость.
Теорема1Пусть f дифференцируема на (a,b). Тогда
1.условие 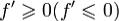 на (a,b) необходимо и достаточно для того, чтобы функция f возрастала (убывала) на (a,b);
на (a,b) необходимо и достаточно для того, чтобы функция f возрастала (убывала) на (a,b);
2.условие f' > 0(f' < 0) на (a,b) достаточно, чтобы функция f строго возрастала (строго убывала) на (a,b).
Теорема 2. Ферма.Пусть x0 - точка экстремума функции f. Тогда производная f'(x0) либо не существует, либо f'(x0) = 0.
Теорема 3.(достаточное условие строгого экстремума)
Пусть f непрерывна в точке x0 и дифференцируема на 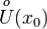 . Пусть
. Пусть 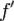 меняет знак при переходе через точку x0. Тогда x0 - точка строгого экстремума.
меняет знак при переходе через точку x0. Тогда x0 - точка строгого экстремума.
Теорема 4.Пусть 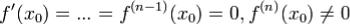 . Тогда
. Тогда
1. при четном n = 2k, x0 - точка строгого экстремума (строго минимума)
при 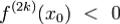 (при
(при 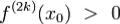 );
);
2. при нечетном n = 2k + 1, x0 - точка возрастания (точка убывания)
при 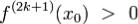 (при
(при 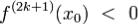 ).
).
Теорема 1 (условие выпуклости функций).
Пусть функция f имеет вторую производную f'' на (a,b). Тогда
1 условие 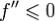 на (a,b) необходимо и достатчно для выпуклости вверх функции f на (a,b);
на (a,b) необходимо и достатчно для выпуклости вверх функции f на (a,b);
2 если f'' < 0 на (a,b), то функция f строго выпукла вверх на (a,b).
Теорема 2 (необходимые условия точки перегиба).
Пусть x0 - точка перегиба функции и f'' непрерывна в x0. Тогда f''(x0) = 0.
Теорема 3 (достаточные условия точки перегиба).Пусть 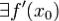 , а f'' меняет знак при переходе через точку x0.Тогда x0 - точка перегиба.
, а f'' меняет знак при переходе через точку x0.Тогда x0 - точка перегиба.
Теорема 4 (о расположении кривой относительно касательной).
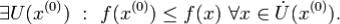
1 Если f''(x0) > 0(f''(x0) < 0), то 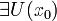 : кривая y = f(x) лежит строго выше
: кривая y = f(x) лежит строго выше
(строго ниже) касательной y = f(x0) +f'(x0)(x •| x0) при 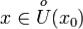 .
.
2 Если 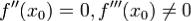 , то
, то 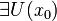 : кривая y = f(x) переходит через
: кривая y = f(x) переходит через
касательную, т.е. при x< x0 и 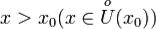 лежит строго по разные стороны от касательной.
лежит строго по разные стороны от касательной.
7.Теорема о равномерной непрерывности функции непр на компакте.
Теорема (Кантор). Пусть 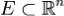 - компакт , и функция f непрерывна на E. Тогда f равномерно непрервына на E.
- компакт , и функция f непрерывна на E. Тогда f равномерно непрервына на E.
8.Достаточные условия дифференцируемости функции нескольких
переменных.
Теорема. Пусть в точке x(0) непрерывны все частные производные
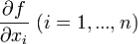 функции f. Тогда f дифференцируема в точке x(0).
функции f. Тогда f дифференцируема в точке x(0).
9. Теорема о неявной функции нескольких переменных.
Пусть функция F двух переменных удовлетворяет следующим условиям: 1. F непрерывна в некоторой окрестности U(x0,y0) точки (x0,y0);
2 F(x0,y0) = 0;3 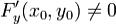 , F'y непрерывна в точке (x0,y0).
, F'y непрерывна в точке (x0,y0).
Тогда существует прямоугольная окрестность точки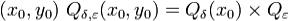 такая, что на
такая, что на
ней ,где функция
,где функция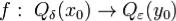 непрервна на Qδ(x0),f(x0) = y0.
непрервна на Qδ(x0),f(x0) = y0.
10. Экстремумы функций нескольких переменных. Необходимые условия, достаточные условия.
Определение. Пусть функция f определена на некоторой окрестности точки x(0). Точка x(0) называется точкой минимума функции f, если
Необходимые условия экстремума. Пусть функция f имеет в точке
экстремума x(0) частную производную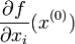 . Тогда
. Тогда 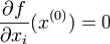 . Определение. Точка x(0) называется стационарной точкой функции f,
. Определение. Точка x(0) называется стационарной точкой функции f,
если f дифференцируема в точкеx(0) и 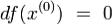 .
.
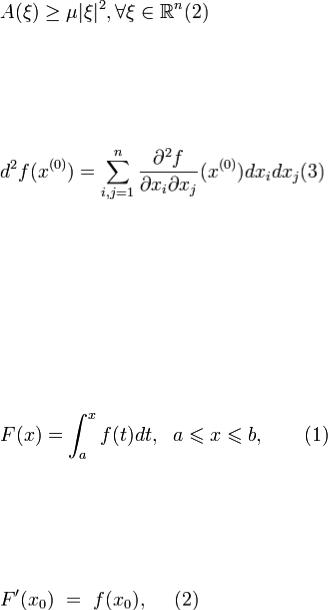
Лемма: Пусть квадратичная форма 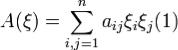 положительно определенна. Тогда при некотором μ > 0
положительно определенна. Тогда при некотором μ > 0
Достаточные условия строгого экстремума. Пусть функция f дважды непрерывно дифференцируема в некоторой окрестности стационарной точки 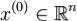 .
.
Пусть второй дифференциал d2f(x(0)) функции f в точке x(0)
является положительно определенной (отрицательно) квадратичной формой. Тогда x(0) - точка строгого минимума (максимума) функции f. Если же квадратичная форма d2f(x(0)) является неопределенной, то в точке x(0) нет экстремума.
11. Свойства интеграла с переменным верхним пределом (непрерывность, дифференцируемость). Формула Ньютона-Лейбница.
Пусть f интегрируема на [a,b]. Тогда на [a,b] определена функция
называемя интегралом с переменным верхним пределом.
Теорема 1. Пусть f интегрируема на [a,b]. Тогда F непрерывна на [a,b]. Теорема 2. Пусть функция f интегрируема на [a,b] и непрерывна в точке 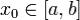 . Тогда функция F(x)имеет производную в точке x0 и
. Тогда функция F(x)имеет производную в точке x0 и
Теорема 3.Пусть функция f непрерывна на (a,b). Тогда она имеет
на (a,b) первообразную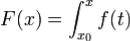 , где
, где 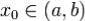 .
.
Основная теорема интегрального исчисления. Пусть функцияfнепрерывнана отрезке [a,b] и Φ - её первообразная на этом
отрезке. Тогда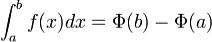 .Это называется формулой НьютонаЛейбница.
.Это называется формулой НьютонаЛейбница.
12. Равномернаясх-сть функциональных последовательностей и рядов.
Определение. Говорят, что функциональная последовательность
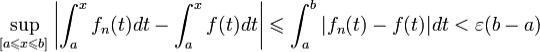
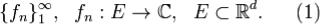 сходится на множестве E равномерно к функции
сходится на множестве E равномерно к функции 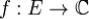 , если
, если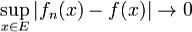 при
при 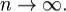
При этом пишут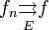 .
.
Критерий Коши равномерной сходимости последовательности.Последовательность 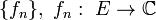 , сходится на E равномерно тогда и только тогда, когда выполняется условие Коши:
, сходится на E равномерно тогда и только тогда, когда выполняется условие Коши:
 .
.
Определение. Говорят, что ряд сходится на E равномерно, если последовательность {Sn} его частичных сумм сходится на E равномерно.
Непрерывность, интегрируемость и дифференцируемость суммы равномерно сходящегося ряда.
Непрерывность. Пусть 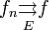 . Если все функции fn непрерывны в точке x(0) по множеству E, то и предельная функция f непрерывна в точке x0 по множеству E.
. Если все функции fn непрерывны в точке x(0) по множеству E, то и предельная функция f непрерывна в точке x0 по множеству E.
Интегрируемость. Пусть функции fn непрерывны на отрезке 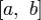 при
при
всех 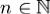 и
и 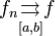 при
при 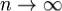 .Тогда
.Тогда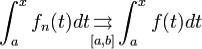 при
при 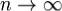 . Доказательство. Функция f(x) по теореме 1 непрерывна на отрезке [a,b] при всех
. Доказательство. Функция f(x) по теореме 1 непрерывна на отрезке [a,b] при всех 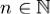 и, следовательно интегрируема на [a,b]. Пусть
и, следовательно интегрируема на [a,b]. Пусть 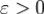 . Тогда в силу равномерной сходимости {fn} к функции f
. Тогда в силу равномерной сходимости {fn} к функции f 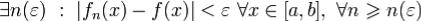 .
.
Следовательно для всех 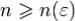
откуда и следует утверждение теоремы.
Для рядов достаточно положить 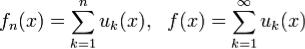 . Дифференцируемость. Пусть последовательность {fn} непрерывно дифференцируемых на отрезке [a,b]функций сходится в точке
. Дифференцируемость. Пусть последовательность {fn} непрерывно дифференцируемых на отрезке [a,b]функций сходится в точке 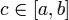 , а, последовательность производных {f'n} равномерно сходится на[a,b] к некоторой функции φ. Тогда последовательность {fn} равномерно сходится
, а, последовательность производных {f'n} равномерно сходится на[a,b] к некоторой функции φ. Тогда последовательность {fn} равномерно сходится
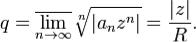
на [a,b] к некоторой функции непрерывно дифференцируемой на [a,b] функции f и f' = φ, так что 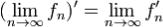 на [a,b].
на [a,b].
.Для рядов достаточно положить 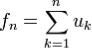 .
.
13. Степенные ряды. Радиус сходимости.
Определение. Функциональный ряд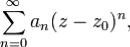
где an и z0 - комплексные числа, а z - комплексная переменная, называется степенным рядом.
Определение. Радиусом сходимости степенного ряда (1) называется число
или 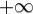 :
: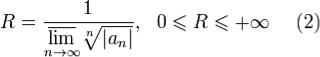 кругом сходимости ряда (1) называется круг
кругом сходимости ряда (1) называется круг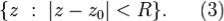
Круг сходимости является открытым множеством. При 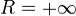 он совпадает со всей комплексной плоскостью.
он совпадает со всей комплексной плоскостью.
Формула (2) называется формулой Коши-Адамара.
Теорема. Признак Коши. Пусть в 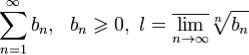 . Тогда
. Тогда
1.при l < 1 ряд сходится
2.при l > 1 ряд расходится и даже общий член не стремиться к нулю.
Теорема. Пусть R - радиус сходимости ряда. Тогда
1.при | z | < R ряд сходится и даже абсолютно.
2.при | z | > R ряд расходится и даже общий член не стремится к нулю. Теорема. Пусть R - радиус сходимости степенного ряда, 0 < r < R. Тогда в круге 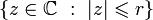 ряд сходится равномерно.
ряд сходится равномерно.
Бесконечная дифференцируемость суммы степенного ряда.
Пусть R > 0 - радиус сходимости ряда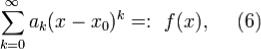
ak - вещественные числа.Тогда при | x •| x0 | < R f имеет производные всех порядков, которые находятся почленным дифференцированием;
Ряд Тейлора.
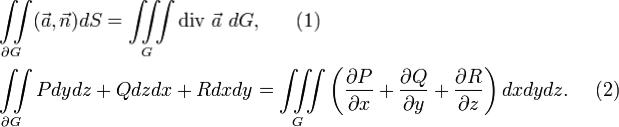
Если функция 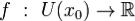 определена в некоторой окрестности точки
определена в некоторой окрестности точки 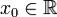 и имеет в точке x0производные всех порядков (т.е. является бесконечно дифференцируемой в точке x0), то степенной ряд
и имеет в точке x0производные всех порядков (т.е. является бесконечно дифференцируемой в точке x0), то степенной ряд
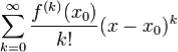 называется рядом Тейлора функции f в точке x0.
называется рядом Тейлора функции f в точке x0.
14. Формула Грина.
Пусть функции P(x,y) и Q(x,y) непрерывно дифференцируемы в односвязной области  , а простой кусочно гладкий контур
, а простой кусочно гладкий контур 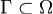 ограничивает область
ограничивает область 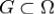 . Тогда справедлива формула
. Тогда справедлива формула
Грина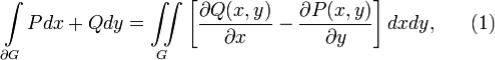 где
где 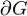 есть положительно ориентированная граница области G.
есть положительно ориентированная граница области G.
Потенциальные векторные поля на плоскости.
Векторное поле 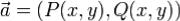 , заданное на области
, заданное на области 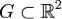 , называется потенциальным в области G, если существует непрерывно
, называется потенциальным в области G, если существует непрерывно
дифференцируемая функция 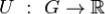 такая, что
такая, что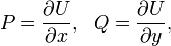 на G. Функцию U называют при этом потенциальной функцией поля
на G. Функцию U называют при этом потенциальной функцией поля 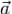 или потенциалом поля
или потенциалом поля 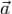 .
.
15.Формула Остроградского-Гаусса.
Пусть 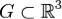 - ограниченная область, граница которой
- ограниченная область, граница которой 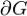 есть кусочно гладкая поверхность, ориентированная внешними нормалями.
есть кусочно гладкая поверхность, ориентированная внешними нормалями.
В 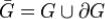 задано непрерывно дифференцируемое векторное поле
задано непрерывно дифференцируемое векторное поле 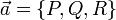 . Тогда поток векторного поля
. Тогда поток векторного поля 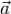 через границу области
через границу области 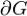 равен тройному интегралу от
равен тройному интегралу от 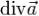 по области G, т.е.
по области G, т.е.
, или
Соленоидальные векторные поля.
Кусочно гладкую поверхность, являющуюся границей ограниченной односвязной области, в дальнейшем для краткости будем называть допустимой. Непрерывно дифференцируемое в области G поле 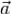 будем
будем
называть соленоидальным, если поток вектора 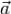 через любую допустимую поверхность
через любую допустимую поверхность 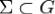 равен нулю.
равен нулю.
16.Формула Стокса для простой гладкой поверхности.
Пусть в ориентированном евклидовом пространстве задана простая поверхность Σ уравнением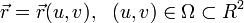 .(1)
.(1)
Здесь Ω - замкнутая область, граница которой есть положительно ориентированный гладкий (или кусочно гладкий) контур (при обходе границы 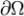 область Ω остается слева). Пусть
область Ω остается слева). Пусть 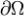 задается уравнениями
задается уравнениями
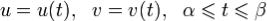 .(2)
.(2)
Образ кривой 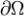 при отображении (1) мы назвали положительно ориентированным краем поверхности Σ и обозначили
при отображении (1) мы назвали положительно ориентированным краем поверхности Σ и обозначили 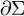 . Напомним, что ориентация поверхности Σ, создаваемаяя полем нормалей
. Напомним, что ориентация поверхности Σ, создаваемаяя полем нормалей 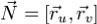 , называется согласованной с положительной
, называется согласованной с положительной
ориентацией края. Было показано, что такое согласование совпадает с известным правилом правого винта.
Пусть в окрестности поверхности Σ задано непрерывно дифференцируемое векторное поле 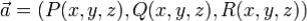 . Если γ - замкнутый
. Если γ - замкнутый
контур, то криволинейный интеграл 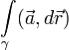 в физике называют циркуляцией векторного поля
в физике называют циркуляцией векторного поля 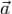 по контуру γ. Если
по контуру γ. Если 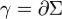 , то говорят, что поверхность Σ натянута на контур γ.
, то говорят, что поверхность Σ натянута на контур γ.
Теорема Стокса.Циркуляция векторного поля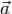 по контуру
по контуру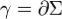 равна потоку вихря этого поля через поверхность Σ, натянутую на контур γ,
равна потоку вихря этого поля через поверхность Σ, натянутую на контур γ,
т.е.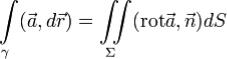 Итак, формула Стокса доказана для простой гладкой поверхности,
Итак, формула Стокса доказана для простой гладкой поверхности,
натянутой на кусочно глакий контур.
17. Теорема о сходимости ряда Фурье в точке.f - 2π периодическая,
абсолютно интегрируемая на[ •| π,π] функция.x0 ¨C еёпочти регулярная
точка f.Тогдаряд Фурье в этой точкеx0 сходится к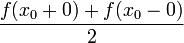 .
.
Если же при этом x0 - регулярная точка f, то ряд Фурье в точке x0 сходится к f(x0).Рассмотрим предел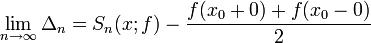

Дробь 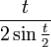 , доопределенная единицей в нуле, является непрерывной на [
, доопределенная единицей в нуле, является непрерывной на [
•| π,π] функцией.Дробь 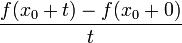 абсолютно интегрируема на [ •| π,π] функция, поскольку таковой является её числитель, и при
абсолютно интегрируема на [ •| π,π] функция, поскольку таковой является её числитель, и при 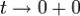 она имеет конечный предел.По теореме Римана об осцилляции, последний интеграл стремиться к нулю при
она имеет конечный предел.По теореме Римана об осцилляции, последний интеграл стремиться к нулю при  , т.е.
, т.е.
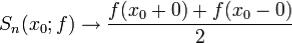 при
при 
Следствие.Пусть 2π - периодическая функция f абсолютно интегрируема на отрезке [ •| π,π], и существуетf'(x0). Тогда ряд Фурье функции f сх. в x0 к f(x0).
18. Дост. условия равномернойсх-сти тригонометрического ряда Фурье.
Пусть f - 2π периодическя и кусочно непрерывно дифференцируемая функция.Тогда ряд Фурье функции f сходится к f равномерно на 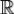 и
и
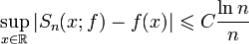 при
при 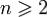 ,где C не зависит от n.
,где C не зависит от n.
19. Преобразование Фурье абсолютно интегрируемой на 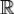 функции есть ограниченная и непрерывная на
функции есть ограниченная и непрерывная на 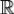 функция.
функция.
Лемма 4.Если f(x) - абсолютно интегрируемая на 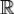 функция, то функции a(y) и b(y), определенные равенствами
функция, то функции a(y) и b(y), определенные равенствами
Преобр Фурье производной и производная преобразования Фурье.
Если непрерывная и абсолютно интегрируемая на 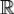 функция f(x) является кусочно гладкой на любом отрезке
функция f(x) является кусочно гладкой на любом отрезке 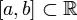 , а функция
, а функция 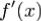 абсолютно интегрируема на
абсолютно интегрируема на 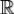 , то
, то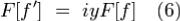 .
.
Л Если функция f(x) непрерывна на 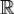 , а функции f(x) и xf(x) абсолютно интегрируемы на
, а функции f(x) и xf(x) абсолютно интегрируемы на 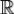 , то функция
, то функция 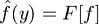 имеет на
имеет на 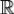 непрерывную
непрерывную
произвудную, причем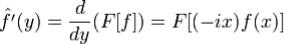 .
.
20. Углы между прямыми и плоскостями.Чтобы найти угол между двумя прямыми, следует найти их напрвляющие векторы и вычислить косинус угла между ними, используя скалярное произведение.
Для нахождения угла между прямой и плоскостью определяют угол θ между направляющим вектором прямой и нормальным вектором
плоскости. Если векторы выбрать так, чтобы 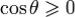 , и взять
, и взять 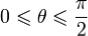 , то искомый угол дополняет θ до π / 2.
, то искомый угол дополняет θ до π / 2.
Угол между плоскостями находят как угол между их нормальными векторами.Для двух прямых на плоскости{ y = k1x + b1, y = k2x + b2 } Получаем
для угла между прямыми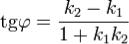 ,если знаменатель зануляется, то получаем, что прямые взаимно перпендикулярны.
,если знаменатель зануляется, то получаем, что прямые взаимно перпендикулярны.
Расстояние от точки до плоскости.
Пусть дана плоскость с уравнением 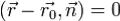 и точка M с радиус-
и точка M с радиус-
вектором R. Рассмотрим вектор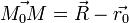 , соединяющий начальную точку плоскости с M. Расстояние от точки до плоскости равно модулю его
, соединяющий начальную точку плоскости с M. Расстояние от точки до плоскости равно модулю его
скалярной проекции на вектор 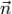 , т.е.
, т.е.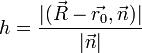 .Если в декартовой прямоугольной системе кооррдинат точка M имеет координаты (X,Y,Z), то
.Если в декартовой прямоугольной системе кооррдинат точка M имеет координаты (X,Y,Z), то
равенство перепишеться в виде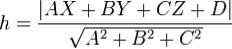
Расстояние от точки до прямой.
Если прямая задана уравнением 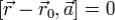 , то мы можем найти расстояние h от точки M с радиус вектором
, то мы можем найти расстояние h от точки M с радиус вектором 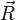 , до этой прямой, разделив площадь параллелограмма, построенного на векторах
, до этой прямой, разделив площадь параллелограмма, построенного на векторах 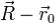 и
и 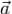 , на длину
, на длину
его основания. Результат можно записать в виде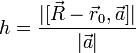
Рассмотрим прямую на плоскости, тогда получаем