
Иванов Матан
.pdf
|
для любого xУсловие2 o (x |
)Æзначение2 (0; Æ0 âf(x)ðìóопределено(1) обеспечивает. Åñëè D =òî,R |
|||||||||||||||||||||||||||
чтовместо Ж 2 (0; Ж |
UÆ 0 |
|
|
|
|
|
(1) можно писать Ж > 0. |
|
f |
||||||||||||||||||||
|
îðìó |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
. |
Òî,0 êàê |
|
|
|
|
|
|
|
|
|
|
определена ли вообще) унк- |
|||||||||
ц яЗамечаниеf точк x0 |
íå |
влияетопределенаlim f(иx). |
|
|
|
|
|
|
|||||||||||||||||||||
|
В частности, если A 2 R, x |
|
|
x!x0 |
|
|
|
|
|
|
|
||||||||||||||||||
|
0 |
|
2 R, а ункция f определена на всей |
||||||||||||||||||||||||||
числовой прямой, то |
|
() |
|
|
|
|
|
|
|
|
|
jf(x) Aj < "); |
|||||||||||||||||
|
1) |
x0 |
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 |
|
|
|
|
+1 ()0 < jx x |
|
j < Æ) ,! (f(x) > 1 ); |
|||||||||||||||||||||
|
3 |
|
lim f(x) = A |
|
|
() |
|
|
jxj > Æ) ,!0 |
(jf(x) Aj < "); |
" |
|
|||||||||||||||||
|
4) |
lim |
|
f(x) = 1 |
|
|
|
() |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
() |
|
x! 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
8" > 0 9Æ > 0 : 8x : (x < 1 ) ,! (jf(x)j > 1 ). |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Æ |
|
|
|
" |
|
. |
|
|
|
ределение в других случаяõ ра писать самосто |
|
|||||||||||||||||||||||||
|
Опpеделение. |
|
Последовательточк x 2 R Síîf1gñòü |
fxng называетсятельнопоследова- |
|||||||||||||||||||||||||
тельностью ейне |
, åñëè |
|
|
|
|
||||||||||||||||||||||||
|
|
|
lim xn = x0 |
è |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
n!1 |
|
|
8n 2 N. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1)2 xn |
=6 x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
предела по ейне. Пусть задàна ункция f : |
|||||||||||||||||||
X !ОпределениеR заданы элементы A 2 |
|
R Sf1g, x0 |
2 R Sf1g, причем |
||||||||||||||||||||||||||
9Æ0 > 0 : |
|
|
o |
(x0) X. Тогда пишут: A = lim |
|
f(x), åñëè äëÿ ëþ- |
|||||||||||||||||||||||
|
UÆ0 |
|
|||||||||||||||||||||||||||
бой последова |
|
|
|
|
|
éíå fx |
|
|
|
|
x!x0 |
|
|
|
|||||||||||||||
|
|
|
|
|
n |
g X предел |
|
|
|
|
|||||||||||||||||||
ff(x |
)g сущесòельностивуетрав |
A. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
n |
|
|
|
|
. Определения предела по Кошипоследовательностиейне эквива- |
||||||||||||||||||||||
|
Òåîpåìà |
||||||||||||||||||||||||||||
лентны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Доказательство. Пусть задана ункция f : X ! R, пусть |
||||||||||||||||||||||||||||
x |
; A 2 R |
|
S |
|
|
o |
|
(x |
|
) X. |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
f1g è U |
Æ0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
деление1) Покажем,пределачтопо изейне.определенияПусть A =пределаlim f(xпо) поКошиКоши,следут. е.т опре- 43 x!x0
|
|
|
|
|
|
|
|
|
|
|
8" > 0 9Æ 2 (0; Æ |
: |
8x 2 |
|
o |
(x |
) ,! f(x) 2 U |
(A): |
|
|
|
(2) |
||||||||||||||||||||
Пусть fx |
|
|
|
|
|
0 |
|
|
|
|
|
UÆ |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
" |
|
|
|
|
|
|
||||||||||
n |
g X про звольная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ейне в точке |
||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=6 x |
|
имеем |
|||||
0 |
. Тогда по определенèю пределапоследовательностьи силу условия x |
n |
0 |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
8Æ > 0 9N : 8n N ,! x |
n |
2 |
o |
Æ |
(x |
): |
|
|
|
|
|
(3) |
|||||||||||||||||
|
|
|
Применим (3) к Ж из (2), тогда |
|
|
|
|
|
|
U |
|
0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8" > 0 9N : 8n N ,! f(x |
n |
) 2 U |
(A); |
|
|
|
|
|
|
|
|
|||||||||||||||||
ò. å. |
|
|
lim f(xn) = A. Значит, A = |
|
lim f(x) ïî åéíå. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
n!1 |
|
|
|
|
|
|
|
|
|
x!x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
2) Методом от |
|
|
|
кажем, что из определения предела |
|||||||||||||||||||||||||||||||||||
A = |
|
lim |
|
|
f(x) по противногоейне, не ïî |
Êîøè. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
по ейне следует определение редела по Коши. Предположим, что |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x!x0 |
|
|
|
9" > 0 : 8Æ 2 (0; Æ |
9x 2 o |
|
(x |
) : f(x) 62U |
|
(A): |
|
|
|
|
||||||||||||||||||||||||
|
|
|
Тогда |
|
|
|
Æ |
" |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
Следовательно, |
|
|
0 |
o |
|
U |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
9" > 0 : 8n 2 N 9xn 2oU |
Æ0=n(x0) : f(xn) 62U"(A): |
xn = x0 è |
|||||||||||||||||||||||||||||
|
|
|
Из условия 8n 2 N ! xn |
2 UÆ0 |
=n(x0) следует, что |
|
lim |
|||||||||||||||||||||||||||||||||||
ейне fx g X акую, что f(x ) 6!A при n ! 1 противоречие. |
||||||||||||||||||||||||||||||||||||||||||
x |
|
|
=6 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n!1 |
|
|
|
|
||||||
n |
0 |
|
|
|
|
8n 2 N. Таким образом, мы получили последовательность |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Свойства пределов ункций |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
Ÿ 2. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
. Åñëè |
|
|
|
n |
|
|
|
|
|
|
|
|
|
9 |
|
lim jf(x)j = jAj. |
|
|||||||||||||
|
|
|
Òåîpåìà |
lim f(x) = A 2 R, |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x!x0 |
|
|
|
|
|
|
|
|
|
|
|
|
x!x0 |
|
|
|
|
|
åéíå â òî÷- |
||||||||
|
|
|
Доказательство. Пусть fxng последто |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
1 èìå |
|
|
|
limf1gj (xn)j = jAj. Пользуясь определениемвательностьйне, |
получаем |
|||||||||||||||||||||||||||||||||||||
ê |
|
|
x0 |
|
2 R S |
, тогда |
lim f(xn) = A. Согласно теор ме 2 Ÿ 4 г |
âû |
||||||||||||||||||||||||||||||||||
требу |
|
|
ое утверждение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Òåîpåìà |
2. Åñëè |
n!1 |
|
|
|
|
|
|
|
lim g(x) = B 2 R, òî |
|
||||||||||||||||||||||||||||
|
|
|
lim f(x) = A 2 R, |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n!1 |
|
x!x0 |
|
|
44 |
|
|
|
x!x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

|
2 |
|
|
9 xlim!x0(f(x) +gg(x(x))))==AA B+,B |
|
|
|
|
|
|
|
|
|
|
|
|
íà |
|||||||||||||||||
|
31) åñëè |
|
|
o |
|
|
|
|
|
|
|
B =6 0 то ункция f(x)=g(x) опред |
|
|
||||||||||||||||||||
в нек торойдополнительноU (x ) 9 lim (f(x)=g(x)) = A=B. |
теорем |
пределе |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
ò ëüñ î. |
|
x!x0 |
1, 2 следуют |
|||||||||||||||||||||||||
|
Докажем |
пункт |
3. ТакПунктыак lim g(x) = B =6 0, топоследовательтеореме 1 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Æ0 |
0 |
|
|
|
|
|
|
|
произведения |
|
|
|
|
|
|
|
|
|
- |
|||
суммы последова ельностей, пределе |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
ностей и определения предела ункции по ейне. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
имеем |
lim |
|
|
|
|
|
|
|
|
|
|
|
x!x0 |
|
jBj, òîã |
|
|
9Æ |
|
> 0 : |
|
8x |
|
|||||||||||
|
jg(x)j = jBj > 0. Возьмем " |
|
|
|
|
|
||||||||||||||||||||||||||||
2 |
U |
|
|
(x ) ,! g(x) =6 0 |
|
ó êö ÿ f(0x)=g(x) î |
|
|
åíà â U |
|
|
(x ). |
||||||||||||||||||||||
Пользуясь |
опредеëåíèåì |
åéíå, èç |
|
î пределе |
частного по- |
|||||||||||||||||||||||||||||
следовательностей получаем требу мое |
ждениовательно,. |
|
|
|
|
|||||||||||||||||||||||||||||
|
o |
Æ0 |
!x0 |
,! |
|
jg(x)j |
|
2 U"(jBj) = |
; 2jBj). Ñëå |
|
|
|
0 |
|
|
|
|
8 |
|
2 |
||||||||||||||
|
( |
|
0) |
|
|
|
|
|
|
|
|
|
o |
|
|
|||||||||||||||||||
|
o |
Æ0 |
|
|
0 |
|
|
|
|
(О предельном перехтеоðåóдемытвернеравенствах.) |
Æ0 |
|
0 |
|
||||||||||||||||||||
|
Ò îp ì 3. |
|
|
Åñëè |
||||||||||||||||||||||||||||||
|
ь омт льст оперех де в неравенствах для последовательностей и оïðå- |
|||||||||||||||||||||||||||||||||
lim |
|
|
f(x) = A 2 R, |
|
lim |
|
g(x) = B 2 R è 9Æ > 0 : |
|
|
|
|
o |
(x0) ,! |
|||||||||||||||||||||
|
|
|
|
|
8x 2 UÆ |
|||||||||||||||||||||||||||||
x |
x0 |
|
|
|
|
|
|
|
|
|
|
x!x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
,! f(x) |
|
g(x), òî A B. |
|
непосредственно из теоремы |
|
î |
|
|
|
|
||||||||||||||||||||||||
|
Äîê |
|
|
|
|
|
|
|
|
следует |
|
|
|
|
|
|||||||||||||||||||
äåëåíия предела ункции по ейне. |
Åñëè lim f(x) = |
|
lim h(x) = |
|||||||||||||||||||||||||||||||
|
Т оp м 4. (О трех ункциях.) |
|
||||||||||||||||||||||||||||||||
= A 2 R è 9Æ > 0 : 8x 2 |
o |
|
x!x0 |
|
|
|
|
x!x0 |
|
|
|
|
|
|||||||||||||||||||||
UÆ(x0) ,! f(x) g(x) h(x), òî |
||||||||||||||||||||||||||||||||||
9 lim |
|
g(x) = A. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x!x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
епосредственно из теоремы о трех по- |
||||||||||||||||||
|
Док т льст о следу т |
|||||||||||||||||||||||||||||||||
следовательностях |
определения предела ункции по ейне. |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
Ÿ 3. |
|
|
Критерий Коши существования прåäåëà |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ункции |
|
|
|
|
|
|
|
|
|
|
2 R Sf1g |
||||||||||||
è |
Л мм 1. Пусть задана ункция f : X ! R. Пусть x0 |
|||||||||||||||||||||||||||||||||
|
|
|
8 ïîñë. åéíå fx |
n |
g X в точке x |
0 |
9 lim f(x |
n |
) = A 2 R: |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
45 |
n!1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда этот предел не зависит от |
|
|
|
|
|
|
|
òî÷ê |
|
|
x0 |
|
|
|
|
|
åéíå: |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
9A 2 R: 8 ïîñë. åéíå fxng X |
|
|
|
|
|
|
,! A = nlim!1f(xn): |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Док т льст о. Пусть имеются две |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
x , |
|||||||||||||||||||||||||||||||||||||||
вательности ейне в точке x : |
последовательностиf g fy произвольныеg, . . lim x |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
lim y |
|
|
= x |
è 8n 2 N ,! |
x |
0 |
|
=6 x |
; |
|
|
y |
|
|
=6 x . |
Составим изпоследоних - |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n!1 |
|
n |
|
|
|
0 |
|||||||
n!1 |
n |
0 |
|
|
|
|
g: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
n |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
следовательность fz |
|
= x |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
kzk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
fz g |
|
y |
|
|
; |
|
å |
k = 2n: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
òüþ |
||||||||||||||||||||
åéíå, |
|
àê êàê |
|
|
|
|
|
|
|
n |
|
|
|
|
|
является |
|
=6 x0 |
. П эвательноому, |
|||||||||||||||||||||||||||||||||||||||
|
lim zk |
|
= x0, 8k 2 N ,! |
|
zk |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
ó |
|
овия леммы, 9 lim |
f(z ). |
àêæÒ êàê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
òè ff(x ñèëó)g |
|||||||||||||||||||||||||||||||||||
ff(y )g являются подпоследовательностпоследовательноями х дящейñя последова- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Последовательностьсостоит том, что |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
k!1 |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|||
|
|
|
|
|
|
|
|
k!1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
определена |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
â |
некоторой |
||||||||||||||||||||||||
|
|
Опp л ни . Пусть ункция |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
lim f(xn) = |
|
|
lim f(yn). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
ьности ff(zk)g, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
o |
|
|
|
|
|
|
|
|
|
|
n!1 |
|
|
|
|
|
|
|
|
|
|
|
n!1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
(x |
|
). У ловие Коши существования предела ункции в точке x |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
U |
Æ0 |
|
0 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
: |
|
8x |
|
; x |
|
|
|
2 |
|
o |
|
(x |
|
) ,! jf(x |
) f(x |
|
j < ": |
|
|
|
|||||||||||||||||||||||||||||||
|
8" > 0 9Æ 2 (0; Æ |
|
|
2 |
|
|
|
|
|
2 |
|
(1) |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
UÆ |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
выпол- |
||||||||||
|
|
Т оp м 1. (Критерий Коши.) 9 lim |
f(x) 2 R () |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x!x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
нено условие Коши существования предела ункции f в точке x0. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Док т льст о. 1) Пусть 9 lim |
|
f(x) = A 2 R, тогда |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
8" > 0 9Æ 2 (0; Æ |
: 8x 2 |
|
ox! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
UÆ |
(x ) ,! jf(x) Aj < "=2: |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
Следовательно, |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
; x |
|
|
2 |
o |
|
(x |
) ,! |
|
jf(x |
) |
||||||||||||||||||||||
|
8" > 0 9Æ 2 (0; Æ |
0 |
: |
|
|
8x |
1 |
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
f(x |
|
)j jf(x |
) Aj + jf(x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UÆ |
|
0 |
|
", ò. å. |
|
|
1 |
|
|
|
||||||||||||||||||||||||
|
|
) Aj < "=2 + "=2 |
|
|
|
выпол- |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
íåíî ó |
|
|
Êîøè (1). |
|
|
|
|
|
|
|
|
|
|
|
|
Коши (1). Возьмем произвольную |
||||||||||||||||||||||||||||||||||||||||||
|
|
2) Пусловие |
выполнено у |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
последоваòельность |
|
ейнесловиеточке |
x0 |
: xn |
! x0 |
, xn |
=6 x0 |
, тогда |
|
(2) |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
8Æ 2 (0; Æ |
|
9N : |
|
|
8n N ,! x |
n |
|
2 o |
|
(x |
|
): |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
46 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UÆ |
0 |
|
|
|
|
|
|
|
|
|
|
||||||||

Используя условие (2) для Ж из (1), получаем |
|
|
|
|
|
|
|
- |
|||||||||||||||||||
. . выполнено8" > 0 9Nó : |
|
8n е КошиN 8k существованияN ,! jf(xn) f(xk)j < "; |
|
||||||||||||||||||||||||
ельности ff(x )g.словВ èëó êðè |
|
|
Коши для последовательностей |
||||||||||||||||||||||||
существуåò |
lim f(xn) = A 2 R. |
|
|
|
|
|
|
в пределаточк x |
|
|
|
9A |
= |
||||||||||||||
|
Èòàê, 8 n!1 |
|
ват льносòерияейне fx g |
|
|
|
|||||||||||||||||||||
= |
|
|
|
|
n |
|
тогда по лемме 1 |
|
|
|
n |
|
|
|
|
0 |
|
|
|
|
|||||||
lim f(xn) 2 R, |
|
|
|
|
|
|
|
|
f(xn): |
|
|||||||||||||||||
|
9A 2 R: |
8послед. ейне fxng X в точке x0 |
,! A = lim |
|
|
||||||||||||||||||||||
|
n!1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n!1 |
|
|
|
|||
Пользуясь определением предела ункции |
|
|
|
|
|
||||||||||||||||||||||
ïî åéíå, |
|
получаем |
|||||||||||||||||||||||||
9 lim f(x) = A 2 R. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x!x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
З ч 1. Пусть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
8" > 0 9A 2 R 9Æ > 0 : 0 < jx x0j < Æ ,! jf(x) Aj < ": |
|
|||||||||||||||||||||||||
Верно ли, что 9 lim |
|
f(x) 2 R? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Ÿ 4. |
|
|
x!x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Ïð ë ïî ìíî ñò ó |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
Ýë ìåíò x |
|
2 R [ f1g называется предельн |
|
||||||||||||||||
множестваОпp Xл ниR, если x 20 X |
|
9Æ > 0 : |
|
o |
(x |
) \ X = ;. |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
. |
Точк x 2 R называется |
|
|
лир ванной точкой |
||||||||||||||||
точкой множ |
|
|
à X R, |
|
|
0 |
|
|
|
|
|
|
|
g X последова- |
|||||||||||||
|
|
. |
если существует f |
n |
|||||||||||||||||||||||
тельность ейестâ òî÷êå x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
жества X Rизолюбой точки x0 2 R |
||||||||||||||
|
Л мм 1. Для любого м |
||||||||||||||||||||||||||
следующиевы 1) x являетснесловияется |
изолированной точкой множества X. |
|
|
||||||||||||||||||||||||
|
(1)2 x |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
UÆ |
|
0 |
|
|
|
|
|
|
|
||
|
|
ó |
|
|
предельнойчк прикосновения множества X (см. Ÿ 11 гла |
||||||||||||||||||||||
|
|
|
|
|
|
|
эквивале тны: |
множества X; |
|
|
|
|
|
|
|||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
òî÷ê |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
предельная точкà ì |
|
|||||||||
|
Äîêò ëüñò î. (1) ) (2). Ïó òü x |
|
|
|
|||||||||||||||||||||||
|
|
|
0 |
|
|
|
lim xn = x0, òî |
силу критерия точки прикосíî- |
|||||||||||||||||||
точкестваx0. Так кдак |
|||||||||||||||||||||||||||
æ |
|
X. Тог существует fx |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
n |
g X последовательность ейне в |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 X, ò. å. |
||||
вения (теорема 1 Ÿ 11 главы 1) справедливо включение x0 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
n!1 |
|
|
|
|
47 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
>x0 0 9n : xn 2точкUo Ж(x0)прикосновениято 8Ж > 0 Uo Ж |
(x0) \ X =6 ;. Следовательно,. Поскольку 8Ж > |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
(2) ) (1). Пусть x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X. |
|
|
|
|
|
|
X è |
|
|
|
||||||||||||||||||||||
|
|
0 |
|
|
|
|
а прик сновения множ |
|
|
x |
|
|
||||||||||||||||||||||||||||||||||||||||
íå являетс |
|
|
|
֐ |
|
|
|
|
|
|
|
|
точкой множества X. Покажем, что |
0 |
||||||||||||||||||||||||||||||||||||||
|
предельная |
|
|
|
|
ìíîæ |
|
|
|
X. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
естваприк |
|
||||||||||||||||||||||||
|
|
àññì òðèì |
|
|
|
|
|
|
|
|
|
|
ê ãäà x |
62X. Òàê êàê x |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
множестваизолированнойслучай,X то силу теоремы 1 Ÿ |
1 главы 1 существуетосноп - |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fxng Xестваакая, что |
lim xn |
= x0 |
. Ò |
|
êàê x0 62X |
|||||||||||||||||||||||||||||||||
венияx 2 X, то |
|
|
|
|
=6 x |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
n!1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
8n 2 N. Поэтому fx g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
следовательностьПу теперь x |
|
|
|
|
2 X. Òàê êàê x |
|
не являетсяпоследовательностьизолир ванной |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
n |
|
|
òî÷ê |
|
x |
n |
|
è, |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
åéíå |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
предельная точк множества |
||||||||||||||||||||||||||||||||
точкой множества Xследовательно,то 8Ж > 0 ! |
|
|
UÆ(x0) \ X =6 ;. Следовательно, |
|||||||||||||||||||||||||||||||||||||||||||||||||
X. |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o 0 |
|
|
|
|
|
|
|
|
|
|
|
|
o |
|
|
|
|
|
|
|
||||
8n 2 N ,! |
|
|
|
(x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
(x ) \ X. |
||||||||||||||||||||
1=n |
|
) \ X =6 ;. Поэтому 8n 2 N 9x |
n |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
U |
|
0 |
|
|
fx g X является |
|
|
|
|
|
|
|
|
|
|
U1=n |
|
0 |
åéíå |
||||||||||||||||||||||||
Последовательностьточк x . |
x |
|
|
ïðå |
|
льная точкпоследовательностьства X. |
þ |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
является |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
0 |
Поэтомуло ункции f : X ! R по множеству X и писать |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
x |
|
2 R[f1g явля тся предельной |
||||||||||||||||||||||
|
|
Опp л ни . Пусть |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
точкой множества X R. |
элементБуговорить,äå 0 |
÷òî |
ýë ìåíò |
A 2 R [f1g |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
(определение |
|
|
|
|
|
|
|
|
|
|
UÆ 0 |
|
|
|
|
|
|
|
|
|
" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
lim f x) = A, åñëè |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
x!x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
Êîøè): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x2X |
|
|
|
|
|
|
|
|
|
|
|
(x ) ,! |
|
f(x) 2 U (A); |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
" > 0 9Æ > 0 : 8x 2 X \ o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
8fxng X ïîñë.åéíå): |
â òî÷ê |
x0 |
|
,! |
|
lim f(xn) = A. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
тность |
определений |
Коши и ейне доказывается так |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n!1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
же,Эквивалеакраньше ( м. доказательство теоремы 1 Ÿ 1). |
è óíêö ÿ f : |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Ç ÷ 1. Ïó |
|
|
|
|
|
заданы множества X |
|
; X |
2 |
|
R |
|||||||||||||||||||||||||||||||||||||||
X |
|
|
[ X |
|
! R. Пусть x |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
è X |
|
. |
||||||||||||||||||||
1 |
|
2 |
0 |
предельная точка множеств X |
1 |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||
Доказать, что |
|
|
|
|
|
, |
|
|
|
|
lim f(x) = A |
|
|
lim f(x) = A!. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
lim |
|
f(x) = A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
x!x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
!x |
0 |
|
|
|
|
|
|
|
|
|
!x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x2X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2X |
|
|
|
|
|
|
|
|
x2X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
[X |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Пpим p. ассмотрим ункцию Дирèõëå: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(x) = |
|
1 |
|
|
|
|
|
Q; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0;48 x 2 R n Q: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||

являетсяНепосредственнопредельнойиз определенийточкой множесследует,в Q ичтоR nлюбаяQ и |
xlimточкаx!2Q f(x)0 |
=2 |
|
1R, |
||||||||||||||||||||||||||||||||||||||||||||||
lim!x |
|
f(x) = 0 |
|
При этом для любой òî÷êè x0 |
2 R предел xlim!x |
|
f(x) |
|||||||||||||||||||||||||||||||||||||||||||
x2RnQ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
не существует. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Ÿ 5. О носторонни пр лы |
|
|
|
|
|
|
íà |
интервале |
||||||||||||||||||||||||||||||||||||||
f(xÎïp0). ë íè |
. |
Пусть |
|
|
óí öèÿ f |
|
определена |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
f â |
|
|
|
x |
|
|
0 |
|
|
|
|
|
|
|
|
|
x!x |
0 |
|
|
|
|
|
|
|
||||||||||||||||||||||
(a; x ). Предел |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
по множеству (a; |
|
|
) называют |
||||||||||||||||||||||||||||||||
пределом лева ункции f вточкê |
|
x |
|
|
|
и обозначают |
|
|
|
lim |
|
f(x) èëè |
||||||||||||||||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Используя определение преäела по множеству, получаем |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
f(x |
|
|
0) = A 2 R [ f1g |
|
|
|
îïð. Êîøè |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
() |
|
|
|
|
|
|
|
|
|
|
|
a) : 8x 2 (x |
Æ; x ,! f(x) 2 U |
(A): |
||||||||||||||||||||||||||||||||||||
|
|
8" > 0 9Æ 2 (0; x |
0 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
f(x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 îïð. |
0 åéíå |
|
|
|
|
|
|
|
" |
|
|
|
|
|
||||||||
() |
|
|
|
0) = A 2 R [ f1g |
|
|
|
|
() |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
8fxng 0 |
(a; x0) : |
|
|
lim xn |
|
= x0 ,! |
|
lim f(xn) = A : |
|
||||||||||||||||||||||||||||||||||||||||
|
Îïp ë íè . |
Пусть |
|
|
|
n!1 |
|
|
|
|
|
|
|
f |
|
|
|
|
n!1 |
|
íà |
интервале |
||||||||||||||||||||||||||||
|
|
|
ункция |
|
|
определена |
|
|
||||||||||||||||||||||||||||||||||||||||||
(x ; b). Предел |
|
|
|
|
|
|
|
f в точке x |
|
|
|
|
по множеству ( |
|
|
|
|
; b) называют |
||||||||||||||||||||||||||||||||
пределом справа ункции f в точке x |
|
|
и обозначают |
|
|
|
|
lim |
|
f(x) èëè |
||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||
f(x0 + 0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x!x +0 |
o |
|
(x |
|
), |
|||||||||||||||
|
Ë ìì 1. |
|
Пусть ункция f опрåäелена в некоторой |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
x 2 R. Тогда |
|
|
() |
|
9f(x0 0) 2 R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UÆ |
|
|
0 |
|
||||||||||||||||||||||||||
90 lim |
f(x) 2 R |
|
|
|
|
è f(x0 + 0) = f(x0 |
|
0) |
: |
|||||||||||||||||||||||||||||||||||||||||
x!x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
. Çàïèшем определение по Коши того, что 9f(x + |
|||||||||||||||||||||||||||||||||||||||||||||
Äîê |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
+ 0) |
= fò(xëüñò0) î= A 2 R: |
9Æ |
|
|
2 (0; Æ |
|
|
; Æ |
|
|
2 (0; Æ |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
8" > 0 |
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
8x 2 (x |
|
|
Æ |
|
; x |
|
|
|
|
; x |
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
(A): |
|
|
|
(1) |
|||||||||||||||
|
|
|
|
|
0 |
1 |
|
) S(x |
0 |
+ Æ |
|
) ,! f(x) 2 U |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
" |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
49 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это условие эквивалентно условию |
|
|
|
|
|
|
|
|
|
A : |
(2) |
|||||||||||||||||||||
|
8x 2 (x |
0 |
Æ; x8)"S> x0 9; xÆ 2+(0Æ;)Æ,!0 : f(x) 2 U |
" |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
0 |
äóåò |
|
|
словие |
(2), ãäå |
|
|||||||
|
|
|
|
|
|
èç |
|
условия |
|
|
|
|
|
|
|
|
|
= |
||||||||||||||
minfЖ1; Ж2g. Из условия |
|
|
|
следуåò |
словие (1), где Ж1 = Æ2 |
|||||||||||||||||||||||||||
Действительно,ìóì èí èìóì, |
Æ; x |
|
|
множества(максимумоf X): |
) |
min f(x) = min(ìàêf X), |
||||||||||||||||||||||||||
= Æ. Òàê |
àê (x |
0 |
) S(x |
; |
0 |
+ Æ) = |
o |
x |
то словие (2) экви |
|||||||||||||||||||||||
валентно |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
UÆ |
|
|
0 |
|
|
|
|
|
|
|||
|
îâèþ A = |
lim (2)f x(1). |
|
|
|
|
|
|
м, ин имумом, супре |
|||||||||||||||||||||||
Îïp ë íè. |
|
|
|
x!x |
|
|
|
ì |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2X |
|
|
|
|
||
sup f(x) = sup fсупремум)(X Минимумотак далее. |
|
|
|
|
|
|
|
|
|
|
|
|
ñè- |
|||||||||||||||||||
м) ункции |
|
f íà |
ножестве X называется минимум |
|||||||||||||||||||||||||||||
x2XНепосредственно из определений ин имума и супремума имеем |
||||||||||||||||||||||||||||||||
m = |
inf |
|
f(x) |
|
|
() |
|
|
|
|
|
x 2 X ,! m |
f(x); |
> f(x); |
|
|||||||||||||||||
|
x2X |
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 X ,! M |
|
||||||||||||||||
|
|
|
|
|
|
|
|
() |
|
|
|
|
8m |
> m 9x 2 X : m0 |
|
|||||||||||||||||
M = sup f(x) |
|
|
|
|
|
|
8M |
0 |
< M 9x 2 X : M0 |
< f(x): |
|
|||||||||||||||||||||
|
x2X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
случае конечных, но и в случае |
|||||||||||
Заметим, что это верно не только |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
. |
|
Функция f |
называется нестрого возрастающей |
|||||||||||||||||||||
бесконечных верхних |
|
|
жних граней. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
на множествеОпp л ниX |
R, |
åñëè |
|
|
|
< x |
|
,! f(x |
) f(x |
): |
|
|
||||||||||||||||||||
|
|
|
8x |
|
; x |
2 |
2 X : x |
1 |
2 |
|
|
|||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
||||
Функция f называется нестрого убывающей на множестве X |
||||||||||||||||||||||||||||||||
R, åñëè |
|
|
8x |
|
; x |
2 |
2 X : |
|
x |
1 |
< x |
2 |
,! f(x |
) f(x |
): |
|
|
|||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
||||
Если ункция |
|
|
|
|
|
я нестрого возрастающей или нестрого |
||||||||||||||||||||||||||
Функция f |
|
называетсявляетсстрого возрастающей на множестве X |
||||||||||||||||||||||||||||||
убывающей,R если |
òî îíà |
|
|
зывае |
x |
я мон тонной. |
|
|
|
): |
|
|
||||||||||||||||||||
|
8x |
|
; x |
2 |
2 X : |
|
1 |
< x |
2 |
,! f(x |
) < f(x |
|
|
|||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
|
|
|
|
||
|
Функция f называется стро о у ы ющ й на множестве X R, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
åñëè |
|
|
|
|
|
8x ; x |
2 |
2 X : |
x |
1 |
|
< x |
2 |
|
,! f(x |
) > f(x |
): |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
Ò îp ì 1. 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
), |
||||||||||||||
òî |
|
Если ункция f нестрого возрастает на (a; x |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
3) |
9f(x |
0 |
0) = |
|
|
|
sup |
|
|
f(x). |
возрастает на (x0; b), то |
|
|
|
0 |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
infa;x0) f(a;x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
2) |
|
|
|
|
|
|
|
x2 |
|
|
0) |
|
|
|
|
|
|
|
|
убывает на (a; x0), то |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
4) Если ункция f нестрого |
убывает на (x |
|
; b), òî |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
9f(x0 |
+ 0) = |
|
|
sup |
|
f(x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
x2(x0;b) |
|
|
|
1) Пусть ункция f нестрого возрастает на |
|||||||||||||||||||||||||||||||||||||||||||||
|
Äîê ò ëüñò î. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
(a; x ). Òàê êàê |
|
онечный или бесконечный супремум любого мно- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
возрастания |
ункции f следует, что 8a;x 2 |
|
|
|
|
|
|
|
, |
|
M1 |
< f(x1) |
||||||||||||||||||||||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
ет, то существует |
|
|
|
|
|
sup |
|
|
f(x) = M 2 |
|
|
f+1g. |
|
||||||||||||||||||||||||||||||||||
жества |
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
M и, кромсуществутого, 8M < M 9x 2 (a; |
|
|
|
|
: M < f(x ). Отсюда и из |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) ,! f(x) |
|
|||||||
|
Из оп ед ле ия супремума следует, что 8x 2 (a; x |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
f(x). |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
1 |
1 |
|
|
0 |
|
1 |
0 |
|
|
|
" |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
8M |
|
< M 9x |
|
2 (a; x |
|
) : 8x 2 (x |
; |
|
|
) |
|
|
M |
|
< f(x) M. |
|||||||||||||||||||||||||||||||||||||||||
|
Èò |
1 |
1 |
|
0 |
|
|
1 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Следовательно,. |
8" > 0 9x 2 (a; x ) : 8x 2 (x ; x ) ,! f(x) 2 U (M), |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
x |
|
|
> 0 : 8x 2 (x |
|
Æ;x |
|
) ,! f(x) 2 U |
(M), à |
||||||||||||||||||||||||||||||||||||||||||||
. . |
|
8" > 0 9Æ = x |
0 |
1 |
|
0 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
значитак,M = f(x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
" |
|
|
|
||||||||||||||
0). |
|
Другие случаи рассмотре ь самостоятель- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Ÿ 6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ункции в |
точке |
|
|
|
|
||||||||||||||||||
|
Опp л Непрерывностьни . 1) Пу ункция f определена в неко орой |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ж-окрестности точки x . Тог |
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ÿ í ïð ðû íîé òî÷ê |
|||||||||||||||||||||||||||||||||||
|
2) Пусть |
|
ункция |
f |
|
|
опрда |
|
|
|
|
|
называетс(a; x . Тогда f называется |
|||||||||||||||||||||||||||||||||||||||||||
x0, åñëè |
lim |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
f(x) = f(x0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
x!x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ëåíàлена[x ; b). Тогда f называется н пр - |
||||||||||||||||||||||||||||||||||||||
|
Пусть ункция f |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
н пр рыспрной в точкопредx , åñëè f(x |
|
|
+ |
0) |
= f(x ). |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
ñë â òî÷ê x |
|
|
, |
|
|
|
ñëè f(x |
|
|
|
|
|
0 |
|
|
|
|
|
). |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
0) = f(x |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
o |
|
(x |
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
3) Пусть f определена в |
|
|
|
|
). Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UÆ |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
51 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
à) åñëè 9 |
x x0 |
|
|
2 R, íî â òî÷ê x0 |
|
|
|
|
f не определена |
||||||||
|
( ), то точка x |
|
|
называетсункцияточкой устр нимо о |
|||||||||||||
ëèáî f(x ) =6 lim |
0 |
|
|||||||||||||||
ð pû;0 f(xx!x0f(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim f(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x!x0 |
|
0) 2 R, íî f(x |
|
|
x0) =6 f(x |
|
+ 0), òî x |
|
xòî÷ê |
||||||||
á) åñëè 9f(x |
0 |
0 |
0 |
||||||||||||||
ð pû ï ð î î0ðî ; |
|
|
|
|
|
|
|
|
|
|
|||||||
+ |
0) |
f(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(x0 |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
x |
в) если какой-либо из |
|
|
|
|
, f(x |
|
|
|
|
||||||||
|
f x 0 |
|
|
+ 0) не существует |
|||||||||||||
или бесконечен, то x |
0 |
точкпределовpы |
òîðî î |
ðî . |
|
|
|
||||||||||
|
|
|
|
|
|
sin(1=x0) |
|
|
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
x |
|
||
|
|
|
|
52 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1=x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
||
|
Ç ÷ 1. |
|
|
|
|
|
|
|
|
|
|
|
|
ет ли ункция |
|
: [x0; x |
|
+ Ж0) ! R, непре- |
||||||||||||||||||||||||||||||||
рывная справа |
Существуточкx и такая, что |
|
|
f(x |
) > 0; f(x |
) < 0: |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
8Æ 2 (0; Æ |
) 9x |
; x |
|
|
02 (x |
|
; x |
0 |
+ Æ) : |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
Ç ÷ 2. |
0 |
|
|
1 |
|
|
|
2 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ет ли ункция f : |
|
R ! R, непрерывная |
||||||||||||||||||||||||||||||||||||
справа в каждойСуществуточкx 2 R и такая, что |
|
) > 0; f(x |
) < 0: |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
8a; b 2 R : a < b 90x |
; x |
2 |
2 (a; b) : f(x |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
Ë ìì 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||
|
|
Пусть f определена в UЖ0 |
(x0). Следующие условия |
|||||||||||||||||||||||||||||||||||||||||||||||
эквивалентны: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
f непрерывна в x ; |
|
|
|
xn = x0 ,! |
|
|
lim f(xn) = f( |
0): |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
1)3 8fxng UÆ0 |
(x0) : |
|
0 |
lim |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
" > 0 9Æ 2 (0; Æ : 8x 2 U (x ,! jf(x) f(x )j < "; |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
Äîê |
|
|
|
|
|
. |
|
|
|
|
|
|
(1) |
|
|
|
, |
|
|
|
(2) |
|
: |
|
|
|
|
|
|
|
åò |
èç |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
n!1 |
|
|
|
|
|
Æ |
|
|
|
0 |
|
|
n!1 |
|
|
|
|
|
0 |
|
=6 x0 |
|
можно |
|||||||||||||||
lim f(x) = f(x0) по Коши; в данном случаеследусловие |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
íå |
|
|
такльсткак |
ïðèî |
x |
|
|
|
x |
|
|
выпол яется: jf(x) f(x )j = 0 < ". |
||||||||||||||||||||||||||||||||||||||
в данном случае |
|
словие x |
|
=6 x |
|
|
можно не |
|
|
|
|
|
|
òàê |
определенияри x = |
|||||||||||||||||||||||||||||||||||
x!x0 |
|
(3) : |
|
|
следует из определения |
lim |
|
f(x) = f(x0) |
|
|
åéíå; |
|||||||||||||||||||||||||||||||||||||||
|
писать,(1) |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
x!x0 |
|
|
|
|
|
0 |
|
|
|
|
|
|||||
|
Ç ÷ 3. Ïó |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
). Как связаны |
|||||||||||||||||||
|
|
|
ункция f определе |
|
писать,в U ( |
|||||||||||||||||||||||||||||||||||||||||||||
= x |
|
выполняется: f(x |
|
|
|
|
|
|
n |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|||||||||
0 |
n |
) = f(x |
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Æ0 |
|
0 |
|
|
|
|
|
|
|
||||
следующие условиясть непрерывностью уíêöèè |
|
|
|
|
? |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
в точке x |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
1) Æ |
|
" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 U" |
(x0) ,! jf(x) f(x0)j < Æ; |
0 |
|
|
|
|
|||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
: 8x : jx x j |
|
|
|
|
|
|
|
|
|
|
|
|
|
< |
"; |
|
|||||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
< |
|
|
,! jf(x) f(x )j |
|
|||||||||||||||||||||||||||||||||
|
5) 8" > 0 9Æ 2 (0; Æ ; |
|
|
9A 2 R : 8x 2 U (x ) ,! jf(x) Aj < "; |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
4 |
|
8 |
|
|
|
|
|
|
|
|
|
9x 2 |
|
o |
Æ |
(x |
) :0 |
jf(x) f(x |
)j < "; 0 |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
U |
|
|
|
0 |
|
|
|
|
|
Æ |
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
53 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
9 |
|
|
: 8x 2 U |
Æ0 |
(x |
|
) ,! jf(x) f(x |
)j < "; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
jx21 |
Ux2(jx<) Æ,!,! jjff((x1)) |
||||||||||||||||
|
86)7 8(условие" <> "0;9Ж 2Липшица)(0; Ж0 : 89xL1; x2 2R U: |
Æ08(x0); x: |
2 |
||||||||||||||||||||||||||||||||||||||||||||||
f(x |
)j |
|
Ljx |
1 |
x |
j. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
Æ0 |
|
|
0 |
|
|
|
|
|
|
1 |
|||||||||
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
f и g определены в U (x ) и |
|
||||||||||||||||||||||||||||
ð |
Т оp м 1. Пусть у |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
точке x . Тогда |
ункции f(x) g(x), f(x) g(x) |
непрерыв- |
|||||||||||||||||||||||||||||||||||||||||||
|
вныточк |
x . Å ëè |
дополнительно g(x ) =6 0, то ункция f(x)=g(x) |
||||||||||||||||||||||||||||||||||||||||||||||
íепрерывна в точке x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Æ |
|
0 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Док т льст о состоит в применении теоремы 2 Ÿ 2. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ункции |
|||
|
Опp л ни. Пусть заданы множества X; Y R |
|
|||||||||||||||||||||||||||||||||||||||||||||||
y : X ! R, f : Y ! R, причем y(X) Y . Функция ' : X ! R, '(x) = |
|||||||||||||||||||||||||||||||||||||||||||||||||
= f(y(x)) называется суперпозицией ункций y |
|
f, èëè |
сложной |
||||||||||||||||||||||||||||||||||||||||||||||
|
ункцией. |
|
|
|
|
|
|
|
|
|
|
|
|
ость сложной |
|
|
|
|
|
|
|
|
|
|
точк .) Пусть |
||||||||||||||||||||||||
|
Ò îp ì 2. (Í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
нкция y |
определенапрерывнекоторой |
U |
|
|
|
(x ) ункциинепрерыв |
|
|
òî÷ê |
x . |
|||||||||||||||||||||||||||||||||||||||
Ïóсть ункция f |
|
|
пределена |
|
|
некоторой U |
|
|
(y ) |
|
|
|
|
í |
|
|
|
|
â |
||||||||||||||||||||||||||||||
|
Äîê ò ëüñò î. Â ñèëó |
непрерывности |
ункции епрерывнаопределенаточк x |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Æ0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
||
точке y = y(x ). Тогда сложная ункция '(x) = f(y(x)) |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
в нек торой U |
|
(x ) и непрерывна |
|
òî÷ê x . |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
0 |
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Æ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(y(x |
|
|
0 |
||||
|
8 > 0 9Æ = |
( ) 2 (0; Æ |
|
: 8x 2 U |
|
(x |
|
) ,! y(x) 2 U |
|
)): |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
(1) |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
Æ |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||||
|
Определим Æ = Æ( ). Òàê àê ïðè x 2 U |
|
(x ) число y(x) при- |
||||||||||||||||||||||||||||||||||||||||||||||
|
В силу непрерыâности |
ункции f в точке y |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Æ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
надлежит множест у определения ункции f, то ункция '(x) = |
|||||||||||||||||||||||||||||||||||||||||||||||||
= f(y(x)) определена в U |
Æ1 |
(x |
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
8" > 0 9 = (") 2 (0; |
|
) : |
|
8y 2 U |
|
|
(y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(f(y |
)): |
(2) |
||||||||||||||||||||||||
|
0 |
|
|
|
|
) ,! f(y) 2 U |
|||||||||||||||||||||||||||||||||||||||||||
|
Èç (1) |
(2) получаем |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
" |
|
|
0 |
|
|
|
||||||||||||||||||
ò. . |
ункция |
'(x) = f(y(x)) непрерывна в точке x . |
|
(f(y(x |
))); |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
8" > 0 9Æ = Æ( (")) : |
|
8x 2 U |
(x |
) ,! f(y(x)) 2 U |
|
|
|||||||||||||||||||||||||||||||||||||||||
Верно ли, что 9 lim |
|
|
|
|
|
|
|
|
|
|
Æ |
|
0 |
x!x0 |
|
|
|
|
|
|
|
|
0 |
" |
|
|
|
|
0 |
|
|
||||||||||||||||||
|
f(y(x)) = A? |
|
|
|
|
|
|
|
|
|
|
y!y0 |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
Пpим p. Пусть x0; y0; A 2 R, |
|
|
lim y(x) = y0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
, lim f(y) = A. |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x!x0 |
|
|
|
|
|
|
|
|
|
54 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||

ешение. Неверно. |
|
Например,A = 0 |
|
y(x) = |
|
0 8x |
2 R, |
f(y) |
= |
||||||||||||||||||||||||||||||||||||||||
x=lim!x0 f(10y;(xy))=6=01:; |
=6 AТогда. |
íî f(y(x)) = |
|
|
1 8x 2 R |
è |
|||||||||||||||||||||||||||||||||||||||||||
Òåîpåìà 3. |
(О замене переменíûõ |
|
|
|
|
предельном переходе.) |
|||||||||||||||||||||||||||||||||||||||||||
Пусть заданы óнкции y : |
U |
|
|
(x ) |
! Rïðèf |
|
|
U |
|
|
|
|
(y ) |
! R, ïóñ ü |
|||||||||||||||||||||||||||||||||||
(a)b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
f(y )следующих= A . . ункция f непрерывнасловий:т чке y ). |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
lim y(x) = y |
2 R, |
|
|
|
|
|
|
|
|
|
|
|
Æ0 |
|
|
0 |
|
|
|
S |
f1g |
|
|
|
0 |
|
0 |
|
|
|
|
|
|||||||||||||||||
|
lim f(y) = A 2 R |
|
|
пусть выполнено хоòÿ |
|||||||||||||||||||||||||||||||||||||||||||||
x!x0 |
9Æ |
|
|
> 0 |
: |
8x 2 U |
|
(x ) ,! y(x) =6 y |
|
èëè |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
y!y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
áû îäíî èç |
|
|
|
|
|
|
o |
дополнительных у |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Òîã |
|
0 |
|
|
|
|
|
|
|
Æ0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
9 lim |
f(òy(x)) = A. |
|
|
|
|
|
|
|
|
|
|
произвольное число " > 0. Так |
|||||||||||||||||||||||||||||||||||
Докда |
|
0 |
|
|
|
|
|
. Пусть задано |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x!x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|||
как lim fзательство(y) = A, |
|
|
|
) : |
|
8y 2 |
|
o |
|
(y |
) ,! f(y) 2 U |
|
(A): |
|
|
|
(3) |
||||||||||||||||||||||||||||||||
y!y0 |
|
|
|
9 2 (0; |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
U |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
" |
|
|
|
|
|
|
|
|
||||||
По определению lim y(x) = y |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
x!x0 |
|
) : |
|
|
|
|
o |
|
(x |
) ,! y(x) 2 U |
|
|
(y |
): |
|
|
|
(4) |
||||||||||||||||||||||||
|
|
|
|
|
9Æ 2 (0; Æ |
|
|
8x 2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
Покажем, что |
|
|
|
|
0 |
|
|
o |
|
|
|
|
|
UÆ |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
8x 2 U |
Æ(x0) ,! f(y(x))o2 U" |
(A): |
|
|
|
|
|
|
|
|
|
(5)4 |
||||||||||||||||||||||||||||||
За иксируем произвольную точку x 2 |
|
U |
Ж(x0). В силу условия |
||||||||||||||||||||||||||||||||||||||||||||||
п лучаем y(x) 2 U |
|
(y |
|
). В случае y(x |
|
=6 y |
0 |
имеем y(x) 2 |
o |
(y |
) è |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
0 |
ó |
|||
согласно (3) включение f(y(x)) 2 U ( |
|
выполнено. ассмот им |
|||||||||||||||||||||||||||||||||||||||||||||||
âèå (b), à ç à÷èò, f(y x)) = f(y ) = |
A 2 U (A). Таким |
|
образом,еализод - |
||||||||||||||||||||||||||||||||||||||||||||||
÷ é y x) = y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
. В этом случае дополнительное условие (a) |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ться не может. Следовательно, реазизуется дополнительное усл |
|||||||||||||||||||||||||||||||||||||||||||||||||
êàçàíî |
соотношение (5). Итак, |
|
0 |
|
(x |
|
|
|
|
|
|
" |
|
|
|
|
|
|
|
|
|
(A): |
|
|
|
||||||||||||||||||||||||
|
|
|
|
8" > 0 9Æ > 0 : 8x 2 |
o |
Æ |
) ,! f(y(x)) 2 U |
|
|
|
|||||||||||||||||||||||||||||||||||||||
Следовательно, |
lim |
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
" |
|
|
|
|
|
|
|||||||||
|
f(y(x)) = A. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
x!x0 |
|
|
|
|
|
|
|
|
|
|
|
|
55 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ОпpеделениеŸ 7. Непрерывность. f : X !ункцииR называетсямножествеí ïð ðû íîé |
||||||||||||||||||||||||||||||||||||
òî÷ê |
|
0 |
2 X ïî ìíî ñò ó X R, åñëè |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
a) |
|
|
|
|
|
x |
|
|
Функцияпредельной точкой |
множества |
X è |
|||||||||||||||||||||||
|
|
точка |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
что соглаявляетсно лемме 1 Ÿ 4 |
|
|
|
|
à x |
|
2 X является |
|
|
|||||||||||||||||||
lim f(x) = f(x |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
) ëèáî |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
x!x |
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x2X |
|
|
|
|
|
|
x |
|
|
|
являетс |
|
|
|
|
|
|
|
точкой множ |
X. |
|
|
||||||||||||||
(b) òî÷ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
гдаЗаметим,точк x являетсизолированн |
|
|
|
òî÷êîé |
|
|
|
|
|
естваслучае,любая |
||||||||||||||||||||||||||
ункция f : X ! |
|
непрерывнаизолированнойточк |
x |
|
ïî |
множествó X. |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
либок - |
||
предельной, либо |
|
|
|
|
|
òî÷ê |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
множества X. В |
|
|
|||||||||||||||||||||||||||
Опpеделение. |
Функция f : X ! R |
|
0 |
|
|
|
|
ÿ í ïð ðû íîé í |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 X ïî |
|||
|
|
ст X R, если f непрерывна называетскаждой точке x0 |
||||||||||||||||||||||||||||||||||
ìíîæ ñòâó X. |
|
Для ункции f : X ! R следующие условия эквива- |
||||||||||||||||||||||||||||||||||
Лемма |
1. |
|
||||||||||||||||||||||||||||||||||
лентны: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
f непр рывна на множестве X; |
|
|
,! |
lim f(x ) = f(x ): |
|
||||||||||||||||||||||||||||
1)3 8x 2 X 8fx g X : |
lim x = x |
|
|
|||||||||||||||||||||||||||||||||
Доказ тельство |
аналогично доказательству леммы 1 Ÿ 6. |
j < "; |
||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
" > 0 9Æ > 0 : 8x 2 U (x ) \ X , jf(x |
|
|
||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
n |
|
|
|
n!1 |
|
n |
Æ |
|
0 |
|
|
n!1 |
|
n |
|
|
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
X; Y |
|
|
|
|
|
|
|
|
||||||
Задача 1. |
|
|
|
Пусть заданы множ |
|
|
|
|
|
|
R и ункции y : |
|||||||||||||||||||||||||
X ! R, f : Y |
|
|
|
! R, y(X) Y , пусть ункция y непрерывна на |
||||||||||||||||||||||||||||||||
множестве X, а ункция f непрерывества |
|
множестве Y . Доказать, |
||||||||||||||||||||||||||||||||||
что сложная ункция '(x) = f(y(x)) непрерывна |
íà |
|
жестве X. |
- |
||||||||||||||||||||||||||||||||
Задача 2. |
|
|
|
Пусть |
|
интервале (a; b) за |
на ункция f. Д к |
|||||||||||||||||||||||||||||
зать, что ункция f непрерывна |
íà (a; b) òîãäà |
и толькмнотогда, когда |
||||||||||||||||||||||||||||||||||
для любых чисел m; M 2 R множества |
fx 2 (a; b) : |
f(x) < Mg |
|
|||||||||||||||||||||||||||||||||
fx 2 (a; b) : |
|
f(x) > mg открыты. |
|
|
|
|
|
|
|
|
|
|
|
|
ì, å |
è èç |
||||||||||||||||||||
Напомним, что множество X R называется к |
|
|
||||||||||||||||||||||||||||||||||
любой |
|
|
|
|
|
|
|
|
|
|
|
|
|
fx g X можно выделитьомпактîäïîñëåäî- |
||||||||||||||||||||||
вательность,последовательностихдящуюсяк |
некоторому x 2 X. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Теоpема 1. Пусть f |
|
n |
|
|
|
|
|
компа те X. Тогда f(X) |
||||||||||||||||||||||||||||
|
|
|
|
|
. (Другими словами,непрерывная унêция переводит ком- |
|||||||||||||||||||||||||||||||
омпактв омпакт.) |
|
|
|
|
|
56 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||

|
|
|
|
|
|
|
ò ëüñò î. |
|
Ïó |
задана |
|
|
|
|
|
|
|
|
|
|
последователь |
|||||||||||||||||||||
ТаклитьностьДокпоакfynyg 2 f(X). тоТребуется9x 2 Xхдок:дящуюсf(азать,x произвольная) = чтоyк .некоторомуВ силуfy gкможноy0 2 fвыде(X)- |
||||||||||||||||||||||||||||||||||||||||||
fy |
|
|
0 |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
n |
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
0 |
|
|
||
|
|
g дпоследовательность,дпоследовательностьости fy |
омпактностиg, х дящая- |
|||||||||||||||||||||||||||||||||||||||
X существует |
|
|
х дящаяся |
|
|
|
|
|
|
|
|
|
|
fxnk g : lim xnk = |
||||||||||||||||||||||||||||
= x |
|
2 X. Â |
|
|
илу непрерывности f имеем |
lim f(x |
|
|
|
|
|
|
k!1 |
|
. å. |
|||||||||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k!1 |
|
|
|
k |
|
|
|
|
|
|
|
|
|||
|
З ч 3. Верно ли, что непрерывная ункция f : R ! R пере- |
|||||||||||||||||||||||||||||||||||||||||
|
k |
|
|
= f(x |
|
) 2 f(X). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|||||||||||||
ñÿ ê y |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
водит |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
ткрытое |
|
|
|
|
æ |
|
|
|
открыт |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
á |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
множество |
|
|
ограниченное; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
â |
|
|
|
|
|
|
|
|
|
|
|
|
|
множество |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
à)ã |
|
замкнутоеграниченноеограниченноезамкнутожество |
в замкнутое и ограни |
|||||||||||||||||||||||||||||||||||||
|
|
Îïp ë íè . |
Последовательность fx g |
|
X называется |
ìè |
||||||||||||||||||||||||||||||||||||
ченное? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
м ксими ирующn |
é) ïîñë î ò ëü |
|||||||||||||||||||||||||
ими ирующ й |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
ответственно |
|
|
lim(соответственноf x ) = sup f(x)). |
|
|
|
lim f(x |
|
) = |
|
inf f(x) (ñî- |
|||||||||||||||||||||||||||||||
остью ункции f на множестве X, если |
|
|
n |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n!1 |
|
|
n |
|
x2X |
|
|
|
n!1 |
|
|
|
|
|
|
|
|
x2X |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
множества X |
|
|
|
|
любой унк |
|||||||||||||||||||||
|
|
Л мм 2. Для любого непу |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
öèè f : X ! R |
|
|
|
|
|
|
|
|
минимизирующая |
|
максимизирующая |
|||||||||||||||||||||||||||||||
|
|
Докт льссуществуо. Поþттеореместогосуществовании |
|
ин имума су- |
||||||||||||||||||||||||||||||||||||||
последовательно |
|
и ункции f на множестве X. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
ществует |
|
|
|
f(x) = m 2 R. Ïî |
определениюрое а мин |
ин имума 8" > 0 9x |
||||||||||||||||||||||||||||||||||||
2 U |
|
|
(m). Таким образом, пос |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
X : |
|
|
|
2X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 X : f(x ) 2 |
||||||||||||||
|
|
f(x) 2 U (m). Следова ель о, 8n 2 N 9x |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
1=n |
|
|
infxng Аналогично строитсÿ ìàêñèìèçирующая последова- |
||||||||||||||||||||||||||||||||||||
тельность. |
|
|
|
|
|
|
" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|||||||||
|
|
|
|
|
|
(Теорема Вейерштрасса.) Если |
|
|
|
|
|
|
|
|
|
f |
непре- |
|||||||||||||||||||||||||
|
|
Ò îp ì 2. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
рывна на компакте X R, то существуют |
|
max2X |
f(x)ункцияmin f(x). |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
Äîê ò ëüñò î. |
|
Обозначим m = |
|
|
|
|
|
|
|
|
|
x2X |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
inf f(x). Â |
силу леммы |
||||||||||||||||||||||||||||||||||||
2 |
существует |
|
минимизирующая |
|
|
|
x2X |
|
|
|
|
|
|
|
|
|
fxng |
|
X: |
|||||||||||||||||||||||
|
последовательность |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
57 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ñòèn |
|
fx |
|
|
) = m. Поскольку X |
|
омпакт, то из |
последовательноfx g, х дящу |
|||||||||||||||||||||||
|
n |
g ìî |
|
|
выделить подп |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x0 2 X. Ïîñê ëüêó |
|
|
|
|
|
|
n |
|
|
|
||||||||||
являетсюс к некоторя подпжно |
|
|
|
|
|
|
|
|
|
k |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
ельностьf (fxf()xgn,kто)g |
||||||||||||||||||||||||
lim f(xn ) = m. Отсюда и из |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
||||||||||||||||
|
последовательностиункц и f следует, |
||||||||||||||||||||||||||||||
k!1 |
|
|
k |
|
|
|
Поэтомуследовательностьюòî÷ê |
стигается min f(x). Существова- |
|||||||||||||||||||||||
÷òî m = f(x ). |
|||||||||||||||||||||||||||||||
|
Îïp |
|
|
|
0 |
|
|
. Функция f : |
непрерывностиX ! R зывается о р |
|
|
|
íà |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2X |
|
|
|
|
|
|
|||
ние максимума доказывается анал гично. |
|
|
|
|
компактенич ннойX R, |
||||||||||||||||||||||||||
X, åñ |
и множество ее значений f(X) ограничено. |
||||||||||||||||||||||||||||||
|
Ñë ñò |
|
1. |
|
Åñëè |
ункция f непрерывна |
|
||||||||||||||||||||||||
in f(x) = m 2 R |
|
|
f(x) = M 2 R. По определению минимóìà |
||||||||||||||||||||||||||||
и максимума ункция f на множестве X |
ограничена |
снизу числом |
|||||||||||||||||||||||||||||
то она огранл ченани |
íà X. |
По теореме |
Вейе штрасса |
|
существ ют |
||||||||||||||||||||||||||
|
Äîê ò ëüñò î. |
|
|
|
|||||||||||||||||||||||||||
x2X |
|
|
|
|
|
|
|
|
|
|
max2X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
m |
|
ограничена сверху числом M. |
|
|
|
|
|
|
|
|
|
|
ñèëó |
||||||||||||||||||
|
Любой отрезок [a; b |
ограничен и замкнут, след вательно, |
|||||||||||||||||||||||||||||
ритерия компактности |
|
|
|
|
|
2 Ÿ 11 главы 1) |
отрезок является |
||||||||||||||||||||||||
существуют |
|
m x f(x) и (теоремаmin f x). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
êомпактом. Отсюда вытекают еще два следствия. |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
Ñë ñò è |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на отрезке [a; b , то |
|||||||||||||
|
3. Если ункция f |
|
|
|
|
|
|||||||||||||||||||||||||
Вернои.) Пусть заданы ункция f, |
непрерывнаяна [a; b , и ÷èñëî y |
|
òà |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x2[a;b |
|
|
|
|
x2[a;b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
она ограничена на [a; b . |
|
|
f |
|
|
|
|
|
|
|
|
[a; b è 8x 2 [ |
b |
|
|||||||||||||||||
|
|
|
|
|
|
|
4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
,! |
||||||||
|
Ç ÷ |
5. |
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
(a; b) è 8x 2 (a;b) |
||||||||||||
|
|
6. Пусть ункция f |
|
|
|
|
|
|
|
R è 9 lim f(x) 2 R. |
|||||||||||||||||||||
,! f(x) > 0. Верно ли, что 9" > 0 : |
|
[ b ,! f(x) "? |
|
|
|
||||||||||||||||||||||||||
8x 2 (a; b) ,! f(x) "? |
|
|
|
||||||||||||||||||||||||||||
|
|
|
ли, что ункция f ограничена |
R? |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Тоp м 3. (Теорема Больцано Коши о промежуто ном зна |
||||||||||||||||||||||||||||||
êèå, ÷òî ëèáî f(a) y |
|
|
f(b), ëèáî f(b) y |
|
|
|
x!1 |
|
|
|
|||||||||||||||||||||
|
|
|
f(a). Тогда сущче- |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
58 |
|
|
|
|
0 |
|
|
|
|
|
0 |
|
||
ствует x0 2 [a; b : f(x0) = y0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||

|
Док т льст о. Пусть, |
|
|
|
|
|
|
|
|
|
|
|
|
|
f(a) y |
0 |
f(b). Обозна- |
|||||||||||||||||||||||||||||||||||||||||||||||||
чим [a0; b0 = [a; b . Пусть определенa +b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
отрезок [ak; bk , причем f(ak) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
y |
|
|
f(b |
). Определим |
|
|
= |
|
|
|
|
k |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
0 |
|
|
|
|
|
|
например, |
|
|
|
y0 |
|
f( k) |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
k[ak+1 |
; bk+1 |
= |
k |
|
a ; |
2 ; |
|
|
|
|
|
åñëè |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
тогда f(a |
k+1 |
) y |
0 |
f(b |
|
|
|
|
[).k; bk ; |
|
|
|
|
|
|
|
|
f( k) < y0; |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; b |
|
g òà |
|
|||||||||
|
Получаем п следоâàòельность вложенных отрезков f[a |
k |
k |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ствует общая |
òî÷ê |
x0 |
|
2 |
|
T |
[ak |
; bk |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
êèõ, ÷òî 8k 2 N ,! f(ak) y0 |
|
f(bk). По теореме Кантора суще |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
тельно, a |
|
|
! x , |
àíàë |
|
2 |
|
k2N |
b |
|
|
|
!x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
Òàê êàê bk |
|
ak |
= |
|
b a |
|
! 0, òî j |
|
0 |
akj jbk |
akj ! 0, |
|
|
|
|
- |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
Òàê êàê f(a ) y |
|
|
|
fгично,(b ) то по |
|
|
|
|
|
|
|
|
|
о предельном |
|
|
следоваде в |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
 ñèëó |
непрерывности |
|
f имеем f(a ) ! f(x ), f(b ) ! f(x ). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
k |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
0 |
|
k |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
k |
|
|
|
|
|
0 |
|
||||||
неравенствах f(x ) y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
f(x ), т.теореме. y = f(x ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ò îp ì 4. |
|
|
Если ункция f |
|
непрерывна на отрезкперех[a; b , то |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
0 |
0 |
|
|
|
|
0 |
|
k |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
f([a; b ) = [m; M , ã |
|
m = |
|
|
|
|
|
|
|
|
|
f(x), M = m x f(x). |
следует, |
÷òî |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Èç |
определений |
|
|
|
|
минимума |
|
|
|
|
|
|
|
максимума |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2[a;b |
|
|
|
|
|
|
|
|
|
x2[a;b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Док т льст о. Еслиmin= M, то отрезок [m; вырождается |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
â äíó |
|
|
÷êó |
|
а ункция f |
|
|
|
|
|
|
|
|
|
константе m = |
M |
íà [a; b . Ïðè |
|||||||||||||||||||||||||||||||||||||||||||||||||
предполагàòü, |
÷òî m < M. |
òðèâнально выполняется. Поэтому будем |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ýò ì |
утверждение теоре |
û |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
÷òî |
|
|
е следует |
|
|
÷òî |
|
; |
|
|
|
|
2 f([a; b ),ленийт. . 9x ; x |
|
|
2 [a; b : f(x ) = m |
||||||||||||||||||||||||||||||||||||||||||||||||||
8x |
2 |
|
[a; b |
! m f(x) |
|
M, ò. . |
|
|
f([a; b ) [m; M . Покаж |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Следовательно,илиСл чкуст .и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ïðåäå |
|
|
|
|
|
минимума |
è |
|
максимума |
|||||||||||||||||||||||||||||||||||||
|
|
|
[m; M f([a; b ). Èç |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
f(x ) = M. Ïî |
|
|
|
|
|
|
|
|
|
|
|
|
|
Êîøè |
|
о пр межут чном значении для |
||||||||||||||||||||||||||||||||||||||||||||||||||
сакжонцамè x |
|
|
x |
|
|
|
теоремеи акая, что f(x ) |
|
= y . |
Поэтому |
y |
|
|
2 f([a; b ). |
||||||||||||||||||||||||||||||||||||||||||||||||||||
любого ч сла y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||||||||
0 |
|
2 [m; M существует точка x |
0 |
, лежащая на отрезкем, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
. |
[m; M f([a; b ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
îò åçîê |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Непрерывная ункция переводит отрезок |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Нап мним, что множес во X R называе |
|
|
ÿ |
числовым проме |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
æóòêîì, |
если X является |
|
|
|
|
|
|
|
|
|
|
ом, точкой, инòервалом, полуинтер- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
валом, лучом (открытым иотрезкзам нутым) или |
âñåé |
числовой прямой. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
59 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пустьinf Тf(оpx) ункция=мm 52. Rf, непрерывнаsup f x) = Mтеорна2числRåìà. Òîвомгдапромежуточномпромежутк значенииX и пусть.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
x2X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2X |
|
|
|
|
|
|
|
|
9x |
|
2 X : |
|
f(x |
) = y |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
8y(Обобщенная2 m; M) |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
÷è ëî |
y |
|
|
2 |
||||||
Док т льст о. Пусть |
задано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
значении существует точк x0, лежащаяпроизвольноеотрезкопределенияс к нцами x1 |
, x2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
2 (m; M). Так как m < y , то из определения ин имума сл |
|
0 |
åò: |
||||||||||||||||||||||||||||||||||||||||||||||||||
9x 2 X : f(x ) < y . Òàê êàê M > y , òî |
|
|
|
|
|
|
|
|
|
|
|
|
|
ñóïð |
äóìà |
||||||||||||||||||||||||||||||||||||||
следует: 9x |
|
|
|
|
|
|
: f(x ) > y . По теореме Коши |
|
|
|
|
межуточном |
|||||||||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
0 |
|
|
|
2 |
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2 X) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
(а значит, x |
|
|
|
àêàÿ, ÷òî f(x ) = y . |
|
|
è |
|
|
|
|
|
|
|
|
|
|
íà ëó÷å |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
9. Пусть |
ункциянепрерывнаяf |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
07 |
|
Доказать, |
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷èñ- |
||||||||||||||
a)б числоâую прямуюинтервал;чтословую |
|
ÿìóþ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
ловой промежуток |
|
числов й промежуток. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Ç ÷ |
|
8. |
Âåð î ëè, |
|
|
|
|
|
|
|
|
|
|
|
|
|
ункция переводит |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
интер ал в |
|
Пусть ункция f |
непрерывнанеограниченалуче [0; +1) |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
Ç ÷ |
|
|
10. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
[0; +1). Верно ли, что |
|
|
|
lim |
f(x) = 1? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x!+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
lim f(x) |
|
= . Верно ли, что выполнено одно из соотношений |
|||||||||||||||||||||||||||||||||||||||||||||||||||
= +1 |
èëè |
|
|
|
lim |
|
f(x) = 1? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
x!+1 |
|
Ÿ 8. |
|
|
|
|
|
|
|
|
|
|
|
x!+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
Обратная ункция |
|
|
|
|
|
|
|
|
|
|
|
. Обратная к |
||||||||||||||||||||||||||||||||||
Л мм 1. Строго монотонная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
Док т льст о. Пункциисть для определенноñòбратимаункция f : X |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
строго возрастающей |
|
|
|
|
|
|
|
|
|
|
|
являетсункциястрого |
озрастающей унк |
|
|||||||||||||||||||||||||||||||||||||||
венство x |
|
|
= x |
|
не может |
|
|
|
|
|
|
|
|
ÿ, |
|
ак ункциивведение)ак f(x = y |
6= y |
= |
|||||||||||||||||||||||||||||||||||
цией; обратная |
|
|
строго |
|
бывающей ункции |
|
рого убывает. |
|
|
|
|
. |
|||||||||||||||||||||||||||||||||||||||||
! X, |
|
|
|
братнойункцииf. Докажем, что ункция f 1 |
строго |
следует об |
|||||||||||||||||||||||||||||||||||||||||||||||
R |
строго возрастает. Из опр делений (см. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
= f(x ). Неравенство x |
|
|
< xвыполнятьссуществованиеакж не может выполняться,возрастак как |
||||||||||||||||||||||||||||||||||||||||||||||||||
ратим |
|
ñòü |
|
|
|
|
|
|
|
|
|
f, ò.å. |
|
. Обозначим x |
|
= f 1(y |
|
f |
1 |
: f(X) |
! |
||||||||||||||||||||||||||||||||
Пусть y |
; y |
2 |
|
2 f(X), y |
1 |
|
< y |
i |
i |
|
(i = |
|
; 2). |
àåò- |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
2 |
|
|
||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
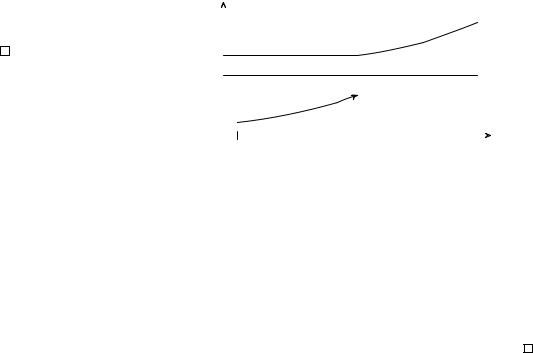
в силу строго возрастания f из условия x |
2 |
< x |
1 |
следу |
, ÷òî y |
2 |
= |
||||||||||||||||||||||||||||||||||||||||||||||
= f(x2) < f(x1) = y1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
. Поэтому выполняется |
|
|
|
|
|
|
|
|
x1 < x2. |
||||||||||||||||||||||||||||||||||||||||||||
Èòàê, 8y |
; y |
2 |
2 f(X) : |
|
|
y |
1 |
< y |
2 |
,! f 1(y |
|
) < fнеравенство1(y ) .ет. |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
f |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
строго возрастает. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
строго монотоннаункция |
|||||||||||||||||||||||||
|
|
|
Ò îp ì 1. |
|
Если ункция f |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
îò ííà è |
непрерывна |
íà [m; M |
|
гопределена,m = fопределена,(a) M = f(b) в случ е |
||||||||||||||||||||||||||||||||||||||||||||||||
|
епрерывна |
|
|
[a; b , то обратная ункция |
|
|
|
|
|
|
|
|
строго мо |
||||||||||||||||||||||||||||||||||||||||
стр го возрастания f и m = f(b), |
M = f(a) в случае |
строго |
убыва |
||||||||||||||||||||||||||||||||||||||||||||||||||
íèÿ f. |
ает. По лемме 1 обратная ункция f |
|
òàêæ |
|
возрас- |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
. |
|
Пусть для |
|
|
|
|
|
|
|
|
|
|
|
1 |
и ункция f строго |
||||||||||||||||||||||||||||
|
|
|
Äîê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
возрастает.По оремет льст4 Ÿо7 f([a; b ) = [m;определенносM , г m = |
min f(x) = f(a), |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Покажем, |
что ункция f |
|
|
|
непрерывнаопределена[m; M . |
Òíàê êàê f |
|
|||||||||||||||||||||||||||||||||||||||||||
M = m x f(x) = f(b). Ñëåä |
|
|
|
|
|
|
|
|
|
|
f |
1 |
|
|
|
|
|
x2[a;b |
|
|
[m; M . |
||||||||||||||||||||||||||||||||
строго возрастает, то по |
теоремевательно,существовании односторонних |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x2[a;b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|||||
пределов |
|
|
|
|
|
|
( |
; |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
sup |
|
|
|
1 |
|
; |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
8y 2 |
|
|
|
|
9f |
|
|
(y |
0) = |
|
|
|
|
f |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
[m; M) |
|
|
|
+ |
|
|
|
inf |
|
|
(y): |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
m y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Осталось доказать, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
! f 1(y |
|
|
|
|
|
|
y2(y0;M) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
8y 2 |
[m; |
M) |
|
|
+ 0) = f 1(y ): |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
; |
|
|
|
|
|
|
|
||||
|
|
|
Предполож м0 противное, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
8y |
Òàê êàê â |
ñèëó |
|
|
|
|
|
|
|
возрастания f |
|
|
|
|
0) = |
|
sup |
|
f 1(y |
|
|
||||||||||||||||||||||||||||||||
< y ,! |
|
f |
1 |
(y) < f |
1 |
(yнапример,) то f 1(y |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
9 |
|
0 |
|
2 (m; M : f 1(y0 |
|
0) =6 f |
1 |
(y0). |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
y2(m;y0) |
|
|
|
|
||||
|
|
|
|
|
|
Поэтомустрогоучетом нашего предположения f 1(y0 |
0) < |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
(y ). |
|||||||||||||||||||||||||||||||||||||||||||||||||||
< f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Следовательно, существует число x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
1(y0 |
0) < x |
|
< f 1(y0): |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
61 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
b = |
|
1 |
(M) |
|
|
f 1(y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1f 1(yx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
f |
|
(y0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
a = f 1(m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
||
|
Используя возрастание ункции f 1, для любого y M2 [m; y |
||||||||||||||||||||||||||||||||||||||
получаем |
|
|
|
|
|
1 |
(y1) |
|
sup |
|
f 1 |
(y) = f 1(y0 |
|
1 |
< x |
0 |
|
|
|||||||||||||||||||||
|
a = f 1(m) f |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
8y 2 [y ; M ,! x < f |
|
(m;y) f |
|
|
|
(y ) f |
|
(M0)= b: |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y2( |
|
0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
противоречие завершает доказательство. |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
2 |
|
0 |
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
|
1 |
2 |
|
|
1 |
|
|
|
|
. Поэтому |
||||||||||
Следоват |
ëüíî, a < x |
|
< b è 8y 2 [m; M ,! f |
= |
(y) =6 x |
||||||||||||||||||||||||||||||||||
x |
2 [a; b |
|
x |
62f |
1 |
([m; M ) |
= |
E |
|
1 |
|
= D |
f |
|
|
[a; b . Полученное |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
òî åñëè |
|
|
|
|
|
f |
||||||||
|
З м ч ни . Аналогично можно доказ ть, |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
ê |
|
|
|
|
строго мо отонна |
|
непр рывна на |
числ в м промежут |
|
||||||||||||||||||||||||||||||
X то обратная у кция |
опред лена, |
|
строго монîòîннаункциянепре- |
||||||||||||||||||||||||||||||||||||
определена,рывна промежутк f(X). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|||||||||||
|
Док т льстТригонометрическиео. ем на оордин тной плоскости |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
Ÿ 9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ункции |
|
|
|
|
|
|
|
|
|||||||||
|
Ë ìì 1. 8x 2 (0; =2) ,! sin x < x < tg x. |
|
|
|
|
|
|
|
|
|
окружак |
|
|||||||||||||||||||||||||||
н сть единичного радиусаНарисуцентром в начàле координат, |
|
||||||||||||||||||||||||||||||||||||||
|
чки O(0; 0), A(1; 0), B( os x; sin x), C( os x; 0) и D(1; tg x). Заметим, |
||||||||||||||||||||||||||||||||||||||
что точка B лежит на прямой (O; D). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
62 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
