
- •(И особенно на потоке в.Т.Петровой)
- •1. Ранг матрицы, определитель матрицы
- •2. Системы линейных уравнений
- •2. Линейные пространства
- •3. Линейные отображения линейных пространств
- •4. Эндоморфизмы линейных пространств
- •5. Линейные формы на линейных пространствах
- •6. Билинейные и квадратичные формы на линейных пространствах
- •7. Скалярное произведение. Евклидово линейное пространство
- •8. Линейные операторы на евклидовых линейных пространствах
- •9. Квадратичные формы на евклидовых линейных пространствах
7. Скалярное произведение. Евклидово линейное пространство
Определить, является ли скалярным произведением на трехмерном линейном пространстве функционал вида:
 где векторы
где векторы и
и заданы своими координатами
заданы своими координатами и, соответственно,
и, соответственно, относительно некоторого базиса этого
пространства.
относительно некоторого базиса этого
пространства.Определить, является ли скалярным произведением на двумерном линейном пространстве функционал вида:
 где векторы
где векторы и
и заданы своими координатами
заданы своими координатами и, соответственно,
и, соответственно, относительно некоторого базиса этого
пространства.
относительно некоторого базиса этого
пространства.Является ли билинейная форма
 на линейном пространстве всех непрерывных
на отрезке
на линейном пространстве всех непрерывных
на отрезке функций скалярным произведением?
функций скалярным произведением?*Является ли билинейная форма
 на линейном пространстве всех
интегрируемых на отрезке
на линейном пространстве всех
интегрируемых на отрезке функций скалярным произведением?
функций скалярным произведением?Пусть
 –
линейные формы на линейном пространстве
–
линейные формы на линейном пространстве .
Определим
.
Определим для любых
для любых .Может ли билинейная
форма
.Может ли билинейная
форма
 – быть скалярным произведением на
– быть скалярным произведением на ?При каких условиях?
?При каких условиях?*Определите какое-либо скалярное произведение на линейном пространстве матриц M
 .
.Определите, является ли скалярным произведением на линейном пространстве квадратных вещественных матриц одного порядка функционал вида
 ,
где
,
где – след (сумма всех диагональных
элементов) произведения матриц
– след (сумма всех диагональных
элементов) произведения матриц .
.*Определите, является ли скалярным произведением на линейном пространстве квадратных комплексных матриц одного порядка функционал вида
 ,
где
,
где – след (сумма всех диагональных
элементов) произведения матриц
– след (сумма всех диагональных
элементов) произведения матриц .
.*Определите, является ли скалярным произведением на линейном пространстве квадратных комплексных матриц одного порядка функционал
 ,
где
,
где – след (сумма всех диагональных
элементов) произведения матриц
– след (сумма всех диагональных
элементов) произведения матриц (
( –
матрица, комплексно сопряженная к
матрице
–
матрица, комплексно сопряженная к
матрице ).
).*Определите, является ли скалярным произведением на линейном пространстве квадратных комплексных матриц одного порядка функционал
 ,
где
,
где – след (сумма всех диагональных
элементов) произведения матриц
– след (сумма всех диагональных
элементов) произведения матриц ,
а
,
а –
матрица, транспонированная к матрице,
комплексно сопряженной матрице
–
матрица, транспонированная к матрице,
комплексно сопряженной матрице .
.Определите, является ли скалярным произведением отображение
 ,
заданное на линейном пространстве
,
заданное на линейном пространстве дифференцируемых и интегрируемых на
отрезке
дифференцируемых и интегрируемых на
отрезке функций формулой:
функций формулой: .
.Докажите, что любая ортогональная система векторов евклидова линейного пространства линейно независима.
Напишите неравенство Коши-Буняковского-Шварца для линейного пространства со скалярным произведением:
 .
.*Докажите, что векторы
 и
и евклидова линейного пространства
евклидова линейного пространства коллинеарны тогда и только тогда, когда
коллинеарны тогда и только тогда, когда .
.Докажите, что для любых векторов
 и
и евклидова линейного пространства
евклидова линейного пространства имеет место неравенство:
имеет место неравенство: .
.Определите, для каких векторов
 и
и евклидова линейного пространства
евклидова линейного пространства имеет место равенство:
имеет место равенство: ..
..Определите, может ли матрица
 быть матрицей скалярного произведения
на трехмерном пространстве?
быть матрицей скалярного произведения
на трехмерном пространстве?Определите, может ли матрица
 быть матрицей скалярного произведения
на трехмерном пространстве?
быть матрицей скалярного произведения
на трехмерном пространстве?Определите, может ли матрица
 быть матрицей скалярного произведения
на трехмерном пространстве?
быть матрицей скалярного произведения
на трехмерном пространстве?Определите, может ли матрица
 быть матрицей скалярного произведения
на трехмерном пространстве?
быть матрицей скалярного произведения
на трехмерном пространстве?*Определите, может ли матрица
 быть матрицей скалярного произведения
на четырехмерном пространстве?
быть матрицей скалярного произведения
на четырехмерном пространстве?Определите, может ли
 быть первой строкой матрицы скалярного
произведения на трехмерном пространстве
относительно его некоторого базиса?
быть первой строкой матрицы скалярного
произведения на трехмерном пространстве
относительно его некоторого базиса?Определите, может ли
 быть второй строкой матрицы скалярного
произведения на трехмерном пространстве
относительно его некоторого базиса?
быть второй строкой матрицы скалярного
произведения на трехмерном пространстве
относительно его некоторого базиса?Определите, может ли
 быть второй строкой матрицы скалярного
произведения на трехмерном пространстве
относительно его некоторого базиса?
быть второй строкой матрицы скалярного
произведения на трехмерном пространстве
относительно его некоторого базиса?Определите, может ли
 быть третьей строкой матрицы скалярного
произведения на трехмерном пространстве
относительно его некоторого базиса?
быть третьей строкой матрицы скалярного
произведения на трехмерном пространстве
относительно его некоторого базиса?Определите, может ли
 быть второй строкой матрицы скалярного
произведения на трехмерном пространстве
относительно его некоторого базиса?
быть второй строкой матрицы скалярного
произведения на трехмерном пространстве
относительно его некоторого базиса?Определите, может ли
 быть второй строкой матрицы скалярного
произведения на трехмерном пространстве
относительно его некоторого базиса?
быть второй строкой матрицы скалярного
произведения на трехмерном пространстве
относительно его некоторого базиса?Определите, может ли
 быть второй строкой матрицы скалярного
произведения на трехмерном пространстве
относительно его некоторого базиса?
быть второй строкой матрицы скалярного
произведения на трехмерном пространстве
относительно его некоторого базиса?*Докажите, что система векторов
 евклидова линейного пространства
линейно независима тогда и только
тогда, когда определитель ее матрицы
Грама положителен.
евклидова линейного пространства
линейно независима тогда и только
тогда, когда определитель ее матрицы
Грама положителен.**Пусть
 и
и – две системы векторов в
– две системы векторов в -мерном
евклидовом линейном пространстве
-мерном
евклидовом линейном пространстве ,
причем система
,
причем система линейно
зависима. Найдите определитель матрицы
линейно
зависима. Найдите определитель матрицы
 ,
где
,
где .
.**Пусть
 и
и – две системы векторов в
– две системы векторов в -мерном
евклидовом линейном пространстве
-мерном
евклидовом линейном пространстве ,
причем система векторов
,
причем система векторов линейно зависима,
а матрица
линейно зависима,
а матрица  ,где
,где  ,
вырожденная. Верно ли, что система
векторов
,
вырожденная. Верно ли, что система
векторов
 линейно зависимая?
линейно зависимая?**Пусть
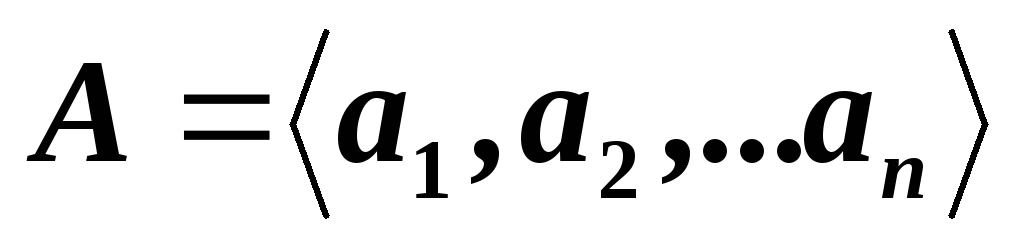 и
и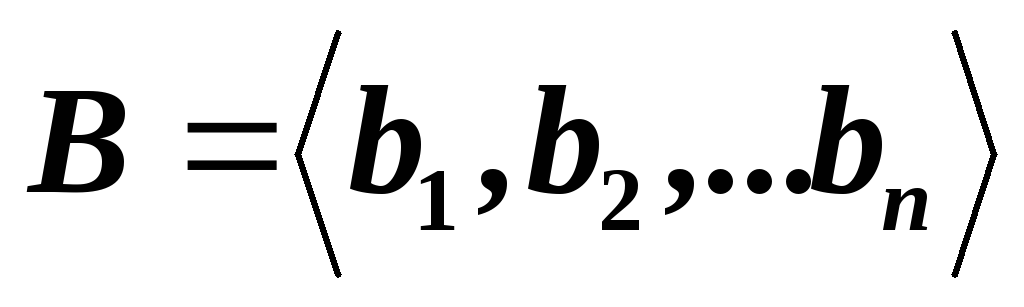 – две системы векторов в
– две системы векторов в -мерном
евклидовом линейном пространстве
-мерном
евклидовом линейном пространстве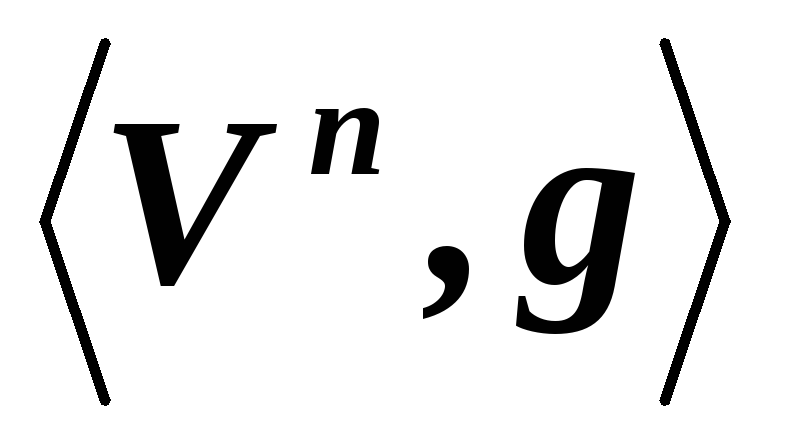 ,
причем система векторов
,
причем система векторов линейно
зависима. Верно ли, что матрица
линейно
зависима. Верно ли, что матрица  ,где
,где  ,
вырождена тогда и только тогда, когда
одна из систем векторов
,
вырождена тогда и только тогда, когда
одна из систем векторов
 или
или линейно зависима?
линейно зависима?**Пусть
 и
и – две системы векторов в
– две системы векторов в -мерном
евклидовом линейном пространстве
-мерном
евклидовом линейном пространстве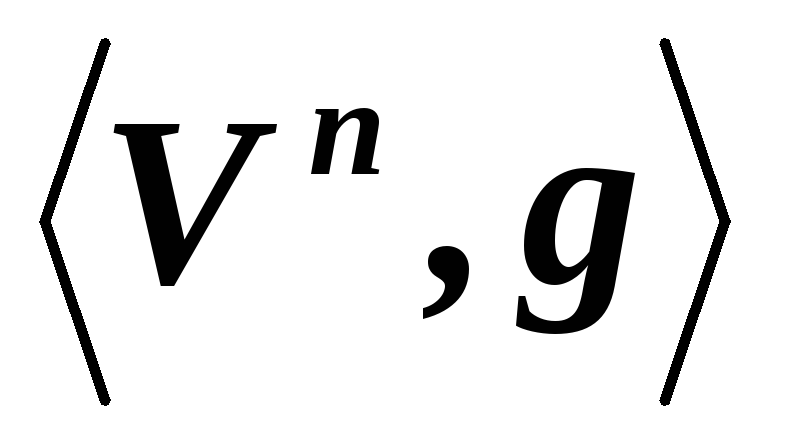 ,
причем система векторов
,
причем система векторов линейно
зависима. Матрица
линейно
зависима. Матрица  ,где
,где  и
и ,
вырожденная. Верно ли, что одна из систем
векторов
,
вырожденная. Верно ли, что одна из систем
векторов
 или
или линейно зависимая?
линейно зависимая?Докажите, что ортогональное дополнение любого непустого подмножества евклидова линейного пространства
 есть подпространство
есть подпространство .
.*Докажите, что, если два подпространства евклидова линейного пространства ортогональны, то их пересечение состоит только из нулевого вектора.
Верно ли, что, если пересечение двух подпространств евклидова линейного пространства состоит только из нулевого вектора, то эти подпространства ортогональны?
*Пусть
 и
и –
подпространства евклидова линейного
пространства
–
подпространства евклидова линейного
пространства
 ,
а
,
а и
и –
их ортогональные дополнения,
соответственно. Можно ли и как через
них выразить
–
их ортогональные дополнения,
соответственно. Можно ли и как через
них выразить  –ортогональное
дополнение к подпространству
–ортогональное
дополнение к подпространству  ?
?*Пусть
 и
и –
подпространства евклидова линейного
пространства
–
подпространства евклидова линейного
пространства
 ,
а
,
а и
и –
их ортогональные дополнения,
соответственно. Можно ли и как через
них выразить
–
их ортогональные дополнения,
соответственно. Можно ли и как через
них выразить  –ортогональное
дополнение к подпространству
–ортогональное
дополнение к подпространству  ?
?Каким должен быть базис евклидова линейного пространства
 ,
чтобы скалярное произведение на нем
имело стандартный вид?
,
чтобы скалярное произведение на нем
имело стандартный вид?Существует ли ортогональная матрица с нулевым определителем? С отрицательным определителем?
Существует ли ортогональная матрица, отличная от единичной, чтобы все ее элементы были бы неотрицательны?
Сумма квадратов элементов строки матрицы равна
 .
Может ли эта строка быть строкой
ортогональной матрицы?
.
Может ли эта строка быть строкой
ортогональной матрицы?Может ли нулевая строка быть строкой ортогональной матрицы?
**Существует ли ортогональная матрица, все элементы которой были бы равны по модулю? В случае положительного ответа приведите пример такой матрицы и укажите, чему равно это число для матрицы порядка
 .
. и
и
 – ортогональные матрицы. Будут ли
ортогональными матрицы
– ортогональные матрицы. Будут ли
ортогональными матрицы и
и ?
?Ортогональна ли матрица
 ,
если
,
если ортогональна, т.е.
ортогональна, т.е. O
O ?
?*Образует ли множество всех ортогональных матриц одного порядка O
 группу относительно операции их
умножения?
группу относительно операции их
умножения?Образует ли множество всех ортогональных матриц одного порядка с положительным определителем SO
 группу относительно операции умножения
(подгруппу O
группу относительно операции умножения
(подгруппу O )?
)?Образует ли множество всех ортогональных матриц одного порядка с отрицательным определителем группу относительно операции умножения (подгруппу O
 )?
)?Образует ли множество всех унитарных матриц одного порядка U
 группу относительно операции их
умножения?
группу относительно операции их
умножения?
