5. Линейные формы на линейных пространствах

335. Линейное пространство четырехмерно, какова размерность его сопряженного (двойственного) пространства?

336. Пусть – линейное пространство многочленов от одной переменной степени не выше , а– его сопряженное пространство, . Отображениесопоставляет каждому многочлену его значение в точке . Линейно ли это отображение?

337. *Пусть – попарно различные точки вещественной прямой, – линейное пространство многочленов от одной переменной степени не выше , а– его сопряженное линейное пространство. ,, причем для любого многочлена, по определению,. Образуют ли линейные формыбазис в пространстве?

338. *Докажите, что для фиксированного (свободного) вектора Vи такого, что отображение V, если, где–скалярное произведение. Найдите матрицу этого отображения относительно ортонормированного базиса, если в этом базисе векторимеет координаты

339. *В координатном линейном пространстве KMзадан базис. Найдите двойственный ему базис в сопряженном пространствеK.

340. **В координатном линейном пространстве KMзадан базис. Найдите двойственный ему базис в сопряженном пространствеK.

341. **Пусть и– базисы линейного пространства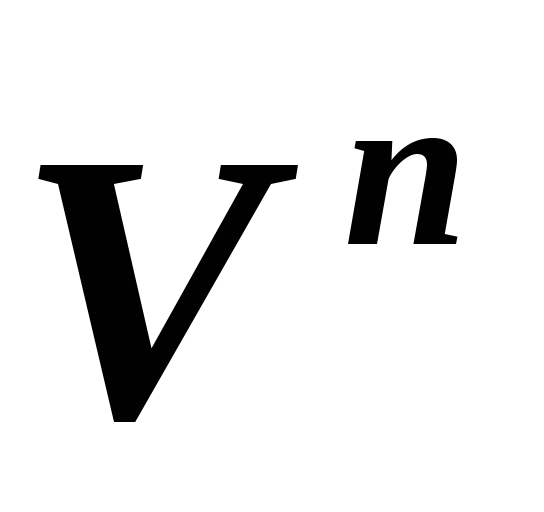с матрицей перехода, аи– двойственные им базисы сопряженного пространства. Найдите матрицу перехода.

342. **Линейная форма задана натак, что , разложите линейную формув линейную комбинацию форм, где, где.

6. Билинейные и квадратичные формы на линейных пространствах

343. Является ли билинейной формой отображение такое, что, где– множество всех непрерывных функций на отрезке?

344. Является ли билинейной формой отображение такое, что, где– множество всех функций, интегрируемых на отрезке?

345. Билинейная форма задана на линейном пространстве. Определите, является ли подпространством этого линейного пространства множество его векторов.

346. Билинейная форма задана на линейном пространстве. Определите, является ли подпространством этого линейного пространства множество его векторов.

347. *Билинейная форма задана на линейном пространстве. Определите наибольшую размерность подпространстваэтого линейного пространства.

348. Может ли одна и та же квадратичная форма порождаться разными билинейными формами?

349. Может ли одна и та же квадратичная форма порождаться разнымисимметрическими билинейными формами?

350. Можно ли по квадратичной форме восстановить порождающую ее билинейную форму? Восстановить порождающую ее симметрическую билинейную форму?

351. Докажите, что билинейную форму на конечномерном линейном пространстве можно привести к диагональному виду, если она симметричная.

352. *Докажите, что билинейную форму на конечномерном линейном пространстве нельзя привести к диагональному виду, если она несимметричная.

353. Верно ли, что квадратичная форма положительно определена на конечномерном линейном пространстве тогда и только тогда, когда ее значения на базисных векторах любого базиса этого пространства положительны?

354. Пусть – линейные формы на линейном пространстве. Определимдля любых.Докажите, что – билинейная форма на.

355. Пусть – линейные формы на линейном пространстве.Определим для любых.Определите условия, при которых эта билинейная форма симметрична.

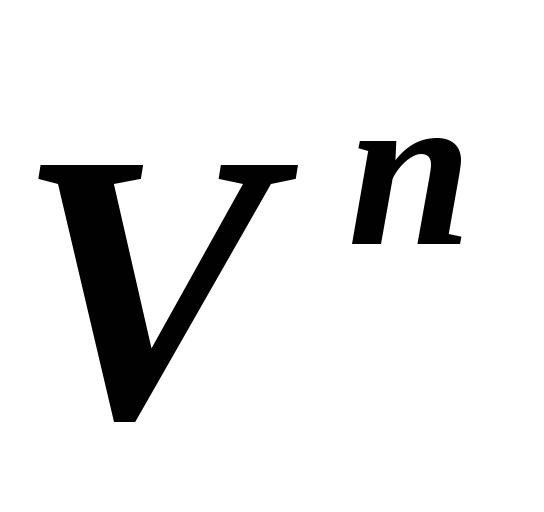356. *Пусть – линейные формы на линейном пространствес матрицамии, соответственно,относительно некоторого базиса в.Относительно этого же базиса найдите матрицу билинейной формы, гдедля любых.

357. Пусть – линейные формы на линейном пространствес матрицамии, соответственно,. некоторого базиса в.Определите условия, при которых билинейная форма где симметрична. для любых.

358. *Определим сумму билинейных форм и произведение скаляра на билинейную форму, положив для любых ,,и. Является ли множество всех билинейных формB на линейном пространстве с такими операциями линейным пространством?

359. *Каждой билинейной форме на линейном пространствесопоставляется ее матрица относительно некоторого базиса. Таким образом определено отображение B M. Докажите, что это отображение биективно.

360. *Каждой билинейной форме на конечномерном линейном пространствесопоставляется ее матрица относительно базиса, и таким образом определено отображение B M. Является ли отображениеизоморфизмом линейных пространствB и M?

361. *Матрица билинейной формына некотором линейном пространствесимметрическая в некотором базисе. Будет ли она обладать таким же свойством в другом базисе этого линейного пространства?

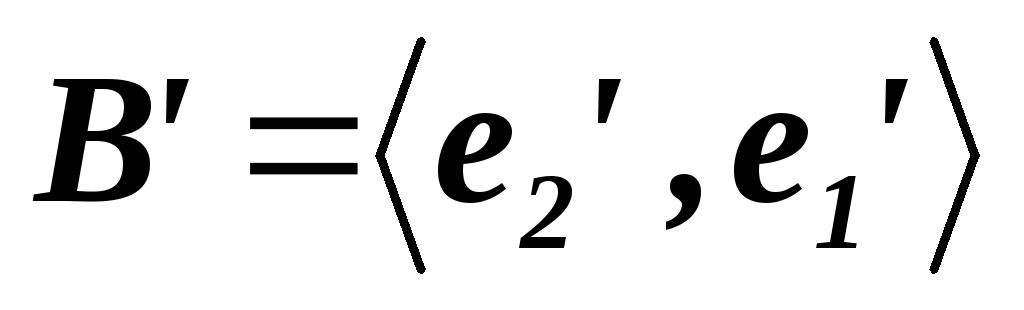362. Изменится ли матрица билинейной формы на двумерном линейном пространстве, если от базиса этого пространства перейти к другому его базисус матрицей перехода?

363. Изменится ли и каким образом матрица билинейной формы , определенной на трехмерном линейном пространстве, если в его базисепоменять местами первых два вектора?

364. Изменится ли и каким образом матрица билинейной формы , определенной на трехмерном линейном пространстве, если в его базисепоменять местами первый и последний векторы?

365. Изменится ли и каким образом матрица билинейной формы , определенной на трехмерном линейном пространстве, если в его базисепервый вектор умножить на 2?

366. Как изменяется матрица билинейной формы, определенной на конечномерном линейном пространстве, если от его базиса перейти к другому его базисус матрицей перехода?

367. Изменяется ли и как именно ранг билинейной формы при замене базиса линейного пространства, на котором она определена?

368. *Как изменится матрица билинейной формы , определенной на конечномерном линейном пространстве, если в его базисе сделать циклическую перестановку векторов?

369. *Как изменится матрица билинейной формы , определенной на конечномерном линейном пространстве, если все векторы его базиса умножить на число?

370. Билинейная форма на конечномерном линейном пространстве имеет в некотором базисе своей матрицейдиагональную матрицу. Верно ли, что в любом другом базисе ее матрица также диагональная?

371. Билинейная форма на конечномерном линейном пространстве имеет в некотором базисе своей матрицейдиагональную матрицу. Верно ли, что в любом другом базисе ее матрица симметрическая?

372. Билинейная форма на конечномерном линейном пространстве такова, что в некотором базисе ее матрица диагональная и все ее элементы положительные. Является ли эта квадратичная форма положительно определенной на этом пространстве?

373. Билинейная форма на конечномерном линейном пространстве такова, что в некотором базисе ее матрица диагональная и все ее элементы неотрицательные. Является ли эта квадратичная форма положительно определенной на этом пространстве?

374. Билинейная форма на конечномерном линейном пространстве такова, что в некотором базисе ее матрица диагональная и все ее элементы отрицательные. Является ли эта квадратичная форма отрицательно определенной на этом пространстве?

375. Изменится ли и каким образом матрица квадратичной формы , определенной на трехмерном линейном пространстве, если в его базисе поменять местами первый и последний векторы?

376. Как изменяется матрица квадратичной формы, определенной на конечномерном линейном пространстве, если от его базиса а перейти к другому его базисус матрицей перехода?

377. Как изменится матрица квадратичной формы , определенной на конечномерном линейном пространстве, если в его базисе сделать циклическую перестановку векторов?

378. Определите положительный индекс инерции квадратичной формы: ?

379. Определите положительный индекс инерции квадратичной формы: ?

380. Определите, является ли положительно определенной на линейном пространстве квадратичная форма?

381. Определите, является ли положительно определенной на линейном пространстве квадратичная форма?

382. Определите, является ли положительно определенной на линейном пространстве квадратичная форма?

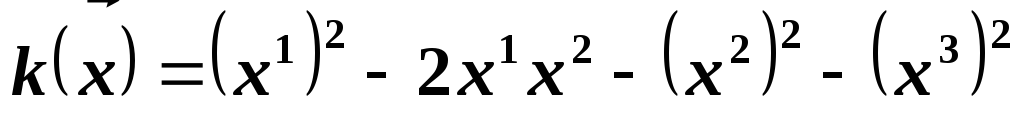383. Определите, является ли отрицательно определенной на трехмерном линейном пространстве квадратичная форма ?

384. Определите, является ли отрицательно определенной на линейном пространстве квадратичная форма?

385. Определите, является ли отрицательно определенной на линейном пространстве квадратичная форма?

386. *Квадратичная форма на конечномерном вещественном -мерном линейном пространстве задана в нормальном виде:, причем. Определите наибольшую размерность подпространства, на которомтождественно равна.

387. **Квадратичная форма на линейном пространствеположительно определена и относительно некоторого базисаимеет матрицей матрицу. Верно ли, что квадратичная формас матрицейотносительно этого же базиса тоже положительно определена?

388. **Докажите, что квадратичная форма на конечномерном линейном пространствеположительно определена тогда и только тогда, когда найдется невырожденная верхняя треугольная матрицатакая, что.

389. *Матрица квадратичной формы на линейном пространствеотносительно некоторого базиса имеет все главные миноры нулевыми. Означает ли это, что данная квадратичная форма вырожденная? Нулевая?

390. Матрица невырожденной квадратичной формы на конечномерном линейном пространстве имеет определитель, равный 1. Может ли она в другом базисе иметь отрицательный определитель?

391. Квадратичная форма на конечномерном линейном пространстве отрицательно определена и имеет определитель, равный . Может ли при переходе к другому базису в качестве матрицы данной квадратичной формы получить матрицу с положительным определителем?

392. Матрица квадратичной формы на конечномерном линейном пространстве имеет главный минор порядка равный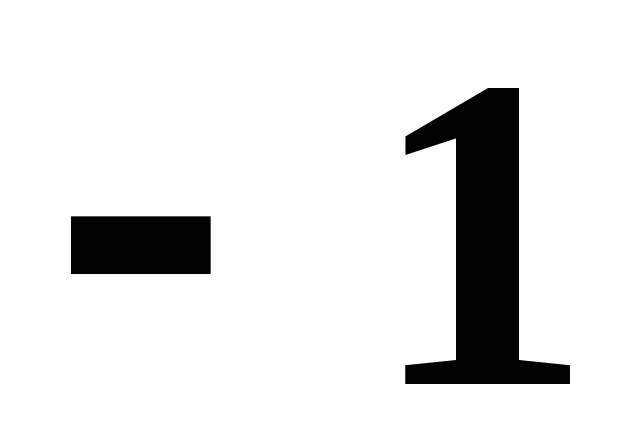. Можно ли в другом базисе этого линейного пространства получить матрицу данной квадратичной формы с положительным главным минором порядка?

393. Квадратичная форма на конечномерном линейном пространстве отрицательно определена, может ли в некотором базисе ее матрица иметь все главные миноры отрицательными?

394. Квадратичная форма отрицательно определена на конечномерном линейном пространстве и имеет канонический вид. Может ли ее матрица в каноническом базисе иметь положительные диагональные элементы?

395. Квадратичная форма положительно определена на конечномерном линейном пространстве и приведена к каноническому виду. Может ли ее матрица в каноническом базисе иметь отрицательные диагональные элементы?

396. Сколько канонических базисов может иметь квадратичная форма, определенная на трехмерном линейном пространстве (базисов, в которых квадратичная форма имеет канонический вид)?

397. *Сколько нормальных базисов может иметь квадратичная форма, определенная на трехмерном линейном пространстве (базисов, в которых квадратичная форма имеет нормальный вид)?

398. Квадратичная форма задана на вещественном линейном пространстве. Определите условия (необходимые и достаточные), при которых найдется ненулевой вектортакой, что.

399. Можно ли для произвольной квадратичной формы на конечномерном вещественном линейном пространстве выбрать базис, в котором ее матрицабыла бы диагональной?

400. Изменяется ли и как именно ранг квадратичной формы при замене базиса линейного пространства, на котором она определена?

401. Квадратичная форма определена на линейном пространстве . Является ли подпространствоммножествовсех векторов, на котором квадратичная форма принимает нулевое значение?

402. Квадратичная форма определена на линейном пространстве . Является ли подпространствоммножествовсех векторов, на котором квадратичная форма принимает неотрицательные значения?

403. Квадратичная форма на -мерном линейном пространстве отрицательно определена. Укажите ее положительный и отрицательный индексы, ранг и сигнатуру.

404. Квадратичная форма на -мерном линейном пространстве положительно определена. Укажите ее положительный и отрицательный индексы, ранг и сигнатуру.