
- •(И особенно на потоке в.Т.Петровой)
- •1. Ранг матрицы, определитель матрицы
- •2. Системы линейных уравнений
- •2. Линейные пространства
- •3. Линейные отображения линейных пространств
- •4. Эндоморфизмы линейных пространств
- •5. Линейные формы на линейных пространствах
- •6. Билинейные и квадратичные формы на линейных пространствах
- •7. Скалярное произведение. Евклидово линейное пространство
- •8. Линейные операторы на евклидовых линейных пространствах
- •9. Квадратичные формы на евклидовых линейных пространствах
4. Эндоморфизмы линейных пространств
Докажите, что если отображения
 ,
то
,
то .
.**Докажите, что
 является линейной алгеброй относительно
естественных операций сложения
эндоморфизмов, умножения их на скаляр
и умножения эндоморфизмов.
является линейной алгеброй относительно
естественных операций сложения
эндоморфизмов, умножения их на скаляр
и умножения эндоморфизмов.Докажите, что для фиксированного (свободного) вектора
 V
V и такого, что
и такого, что отображение
отображение
 ,
если ,
,
если , ,
где
,
где –векторное
произведение. Найдите ядро и образ
–векторное
произведение. Найдите ядро и образ
 .
Определите, сюръективно ли это
отображение? Инъективно? Является ли
.
Определите, сюръективно ли это
отображение? Инъективно? Является ли автоморфизмомV
автоморфизмомV ?
?*Является ли дифференцирование эндоморфизмом линейного пространства всех дифференцируемых функций на отрезке
 ?
В случае положительного ответа укажите
его ядро и образ.
?
В случае положительного ответа укажите
его ядро и образ.*Является ли дифференцирование эндоморфизмом линейного пространства всех многочленов? В случае положительного ответа укажите его ядро и образ.
*Является ли дифференцирование
 эндоморфизмом линейного пространства
линейного пространства
эндоморфизмом линейного пространства
линейного пространства дифференцируемых функций на отрезке
дифференцируемых функций на отрезке ?
В случае положительного ответа укажите
его ядро и образ.
?
В случае положительного ответа укажите
его ядро и образ.Является ли интегрирование эндоморфизмом линейного пространства всех многочленов? В случае положительного ответа укажите его ядро и образ.
Является ли интегрирование эндоморфизмом линейного пространства всех многочленов степени не выше
 ?
В случае положительного ответа укажите
его ядро и образ.
?
В случае положительного ответа укажите
его ядро и образ.*Является ли интегрирование
 эндоморфизмом линейного пространства
эндоморфизмом линейного пространства интегрируемых по Риману функций на
отрезке
интегрируемых по Риману функций на
отрезке ,
где
,
где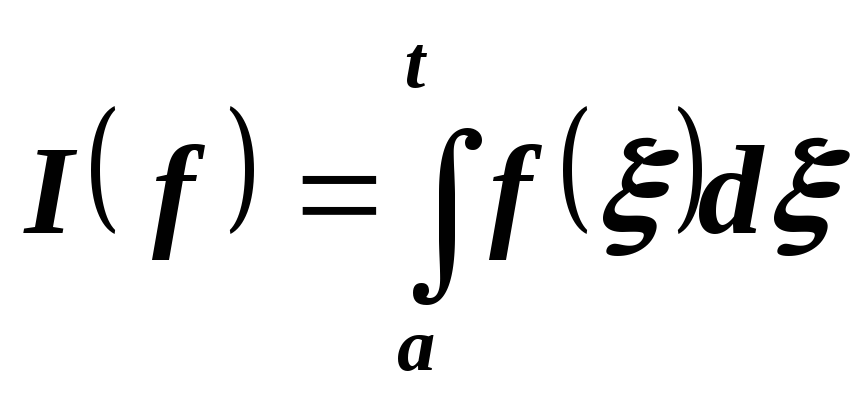 ,
, .
В случае положительного ответа укажите
его ядро и образ.
.
В случае положительного ответа укажите
его ядро и образ.Для фиксированного (свободного) вектора
 V
V и такого, что
и такого, что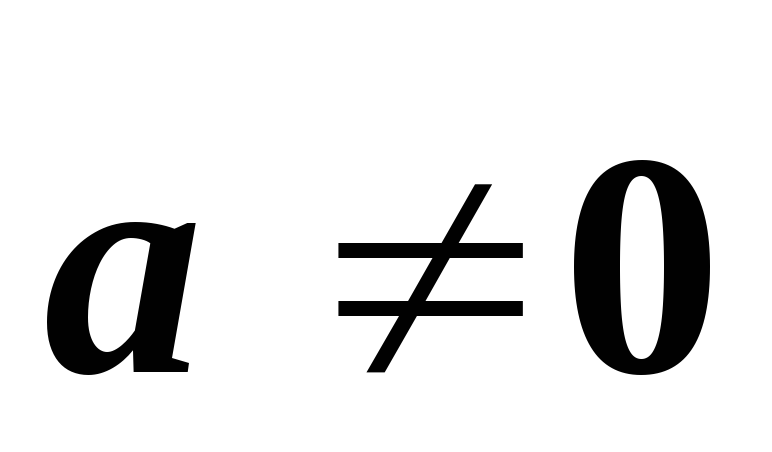 отображение
отображение
 (где
(где –векторное
произведение)
–векторное
произведение)
 .
Найдите матрицу этого отображения
.
Найдите матрицу этого отображения относительно ортонормированного базиса
относительно ортонормированного базиса ,
если в этом базисе вектор
,
если в этом базисе вектор имеет координаты
имеет координаты

Какова матрица дифференцирования многочленов степени не выше
 в стандартном базисе в этом линейном
пространстве?
в стандартном базисе в этом линейном
пространстве?Какова матрица дифференцирования многочленов степени не выше
 в базисе
в базисе этого линейного пространства?
этого линейного пространства?*Какова матрица дифференцирования многочленов степени не выше
 в базисе
в базисе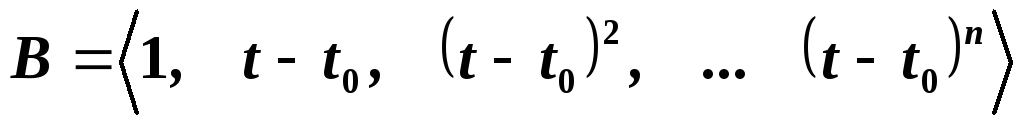 этого линейного пространства?
этого линейного пространства?Является ли проектирование
 линейного пространства всех свободных
(геометрических) векторовV
линейного пространства всех свободных
(геометрических) векторовV на его одномерное подпространствоV
на его одномерное подпространствоV (свободных векторов, параллельных
некоторой прямой) эндоморфизмом
(автоморфизмом) этого пространства?
(свободных векторов, параллельных
некоторой прямой) эндоморфизмом
(автоморфизмом) этого пространства?Является ли проектирование
 линейного пространства всех свободных
(геометрических) векторовV
линейного пространства всех свободных
(геометрических) векторовV на его одномерное подпространствоV
на его одномерное подпространствоV (свободных векторов, параллельных
некоторой прямой) автоморфизмом
пространстваV
(свободных векторов, параллельных
некоторой прямой) автоморфизмом
пространстваV (обратимым эндоморфизмом)?
(обратимым эндоморфизмом)?Является ли симметрия (отражение)
 линейного пространства всех свободных
(геометрических) векторовV
линейного пространства всех свободных
(геометрических) векторовV относительно его одномерного
подпространстваV
относительно его одномерного
подпространстваV (свободных векторов, параллельных
некоторой прямой) эндоморфизмомV
(свободных векторов, параллельных
некоторой прямой) эндоморфизмомV ?
АвтоморфизмомV
?
АвтоморфизмомV (обратимым эндоморфизмом)?
(обратимым эндоморфизмом)?Является ли симметрия (отражение)
 линейного пространства всех свободных
(геометрических) векторовV
линейного пространства всех свободных
(геометрических) векторовV относительно его одномерного
подпространстваV
относительно его одномерного
подпространстваV (векторной прямой) автоморфизмомV
(векторной прямой) автоморфизмомV ?
?Является ли поворот
 линейного пространства всех свободных
(геометрических) векторовV
линейного пространства всех свободных
(геометрических) векторовV на угол
на угол ,
,
 эндоморфизмом
(автоморфизмом) пространства V
эндоморфизмом
(автоморфизмом) пространства V ?
?*Является ли проектирование
 в линейном пространстве
в линейном пространстве на плоскость
на плоскость параллельно векторной прямой
параллельно векторной прямой эндоморфизмом? В случае положительного
ответа укажите его ядро и образ.
эндоморфизмом? В случае положительного
ответа укажите его ядро и образ.*Является ли проектирование
 в линейном пространстве
в линейном пространстве на плоскость
на плоскость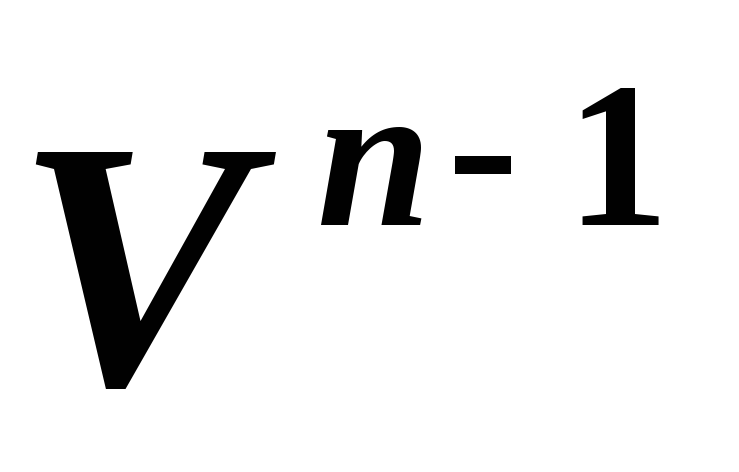 параллельно векторной прямой
параллельно векторной прямой автоморфизмом
автоморфизмом (обратимым эндоморфизмом)?
(обратимым эндоморфизмом)?*Является ли симметрия (отражение)
 относительно подпространства
относительно подпространства в линейном пространстве
в линейном пространстве эндоморфизмом (т.е. любому вектору
эндоморфизмом (т.е. любому вектору ,
где
,
где ,
а
,
а сопоставляется вектор
сопоставляется вектор )?
В случае положительного ответа укажите
его ядро и образ.
)?
В случае положительного ответа укажите
его ядро и образ.*
 ,
верно ли, что
,
верно ли, что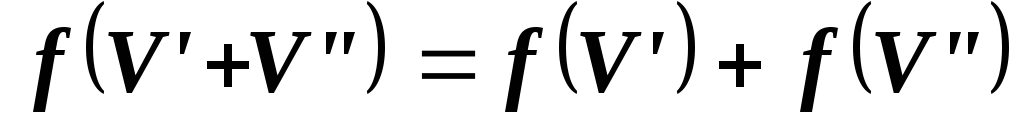 ,
если
,
если и
и –
подпространства линейного пространства
–
подпространства линейного пространства ?
? ,
верно ли, что
,
верно ли, что
 ,
если
,
если и
и –
подпространства линейного пространства
–
подпространства линейного пространства ?
? ,
верно ли, что
,
верно ли, что
 ,
если
,
если и
и –
подпространства линейного пространства
–
подпространства линейного пространства ?
?*
 ,
верно ли, что
,
верно ли, что ,
если
,
если и
и –
подпространства линейного пространства
–
подпространства линейного пространства ?
? ,
верно ли, что
,
верно ли, что
 ,
если
,
если и
и –
подпространства линейного пространства
–
подпространства линейного пространства ?
? ,
верно ли, что
,
верно ли, что
 ,
если
,
если и
и –
подпространства линейного пространства
–
подпространства линейного пространства ?
?Докажите, что, если
 ,
то ядро эндоморфизма
,
то ядро эндоморфизма
 – подпространство, инвариантное
относительно
– подпространство, инвариантное
относительно .
.Докажите, что, если
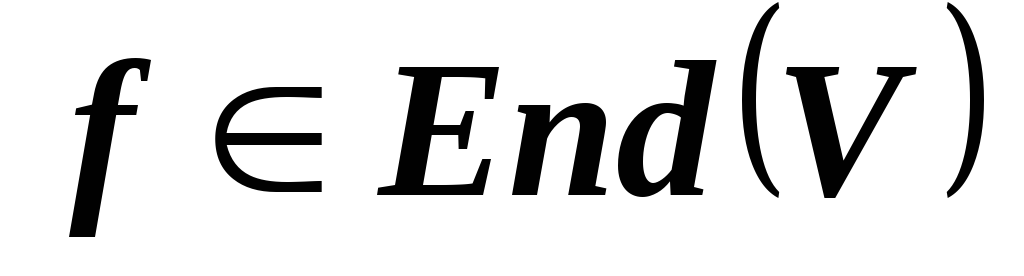 ,
то образ эндоморфизма
,
то образ эндоморфизма
 – подпространство, инвариантное
относительно
– подпространство, инвариантное
относительно .
.Верно ли, что для любого
 любое подпространство
любое подпространство инвариантно?
инвариантно?Верно ли, что для любого
 любое подпространство линейного
пространства
любое подпространство линейного
пространства ,
содержащее
,
содержащее инвариантно?
инвариантно?**Для произвольного
 какое из утверждений верно:
какое из утверждений верно: ,
,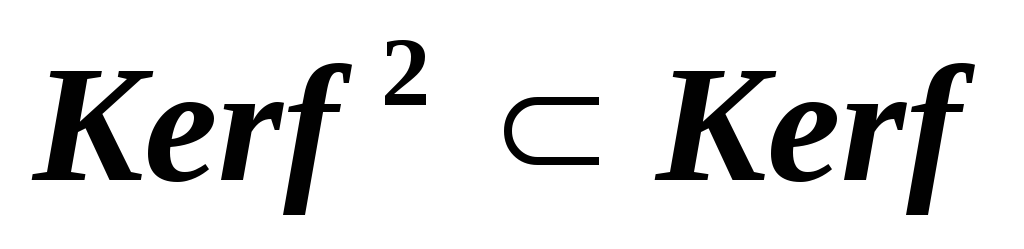 или
или ?
?**Для произвольного
 какое из утверждений верно:
какое из утверждений верно: ,
, или
или ?
?**Верно ли, что равенство
 имеет место для любого
имеет место для любого (
( –
произвольноеконечномерное
линейное пространство)?
–
произвольноеконечномерное
линейное пространство)?**Верно ли, что равенство
 имеет место для любого
имеет место для любого (
( –
произвольное линейное пространство)?
–
произвольное линейное пространство)?*Может ли для эндоморфизма
 выполняться
выполняться ?
?**Пусть
 .
Докажите, что
.
Докажите, что тогда и только тогда, когда
тогда и только тогда, когда .
.*
 ,
как изменится матрица
,
как изменится матрица этого линейного оператора, если в базисе
этого линейного оператора, если в базисе ,
относительно которого она задана,
изменить порядок векторов на
противоположный?
,
относительно которого она задана,
изменить порядок векторов на
противоположный?*
 ,
как изменится матрица
,
как изменится матрица этого линейного оператора, если каждый
вектор базиса
этого линейного оператора, если каждый
вектор базиса ,
относительно которого она задана,
умножить на число
,
относительно которого она задана,
умножить на число ?
?Матрица
 линейного оператора
линейного оператора скалярная в некотором базисе
скалярная в некотором базисе .
Будет ли она обладать таким же свойством
в любом другом базисе этого пространства?
.
Будет ли она обладать таким же свойством
в любом другом базисе этого пространства?Матрица
 линейного оператора
линейного оператора диагональная в некотором базисе
диагональная в некотором базисе .
Будет ли она обладать таким же свойством
в любом другом базисе этого пространства?
.
Будет ли она обладать таким же свойством
в любом другом базисе этого пространства?Матрица
 линейного оператора
линейного оператора симметрическая в некотором базисе
симметрическая в некотором базисе .
Будет ли она обладать таким же свойством
в любом другом базисе этого пространства?
.
Будет ли она обладать таким же свойством
в любом другом базисе этого пространства?Матрица
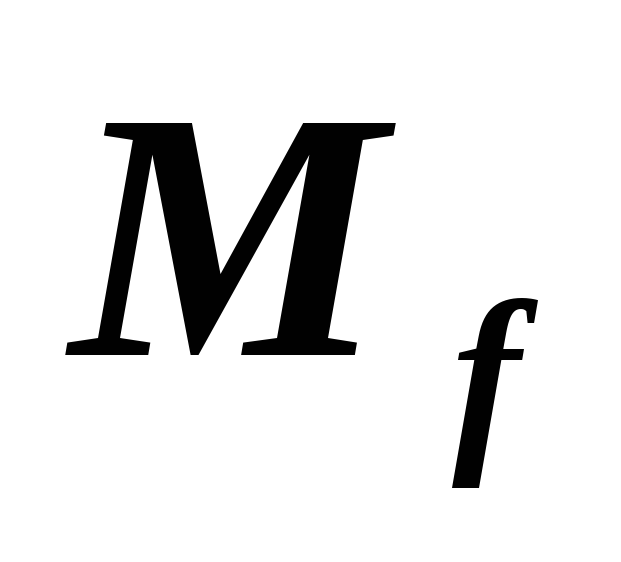 линейного
оператора
линейного
оператора кососимметрическая в некотором базисе
кососимметрическая в некотором базисе .
Будет ли она обладать таким же свойством
в любом другом базисе этого пространства?
.
Будет ли она обладать таким же свойством
в любом другом базисе этого пространства?Пусть
 и
и .
Какова матрица
.
Какова матрица в базисе этого пространства
в базисе этого пространства ,
если векторы
,
если векторы ,
а
,
а ?
?**Пусть
 и
и .
Существует ли базис в
.
Существует ли базис в ,
относительно которого матрица
,
относительно которого матрица диагональная?
диагональная?*Является ли невырожденным (обратимым) эндоморфизм
 линейного пространства
линейного пространства интегрируемых по Риману функций на
отрезке
интегрируемых по Риману функций на
отрезке ,
где
,
где ,
, ?
?Укажите все собственные подпространства эндоморфизма
 M
M
 ,
если
,
если (отображение сопоставляет любой матрице
ее транспонированную матрицу).
(отображение сопоставляет любой матрице
ее транспонированную матрицу).*
 и обратим, т.е. существует
и обратим, т.е. существует .
Является ли
.
Является ли  эндоморфизмом
линейного пространства
эндоморфизмом
линейного пространства
 ?
?Докажите, что если
 и подпространства
и подпространства и
и инвариантны относительно
инвариантны относительно ,
то подпространство
,
то подпространство также инвариантно относительно
также инвариантно относительно .
.Докажите, что если
 и подпространства
и подпространства и
и инвариантны относительно
инвариантны относительно ,
то подпространство
,
то подпространство также инвариантно относительно
также инвариантно относительно .
.*
 (т.е.
(т.е. и существует
и существует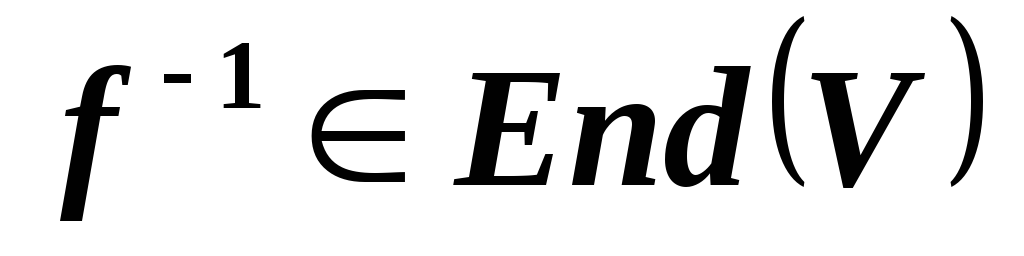 ).
Верно ли, что если
).
Верно ли, что если –
подпространство
–
подпространство ,
инвариантное относительно
,
инвариантное относительно ,
то подпространство
,
то подпространство инвариантно относительно
инвариантно относительно ?
?*Верно ли, что, если
 ,
то
,
то и
и имеют одни и те же инвариантные
подпространства в линейном пространстве
имеют одни и те же инвариантные
подпространства в линейном пространстве ?
?Как меняется с изменением базиса линейного пространства
 характеристический многочлен
характеристический многочлен и характеристическое уравнение
и характеристическое уравнение эндоморфизма
эндоморфизма ?
?Как изменяются собственные значения
 с изменением базиса в линейном
пространстве
с изменением базиса в линейном
пространстве ?
?Докажите, что
 может иметь не более
может иметь не более собственных значений.
собственных значений.Может ли автоморфизм
 иметь нулевое собственное значение?
иметь нулевое собственное значение? и имеет одно из
собственных значений, равное
и имеет одно из
собственных значений, равное
 .
Может ли этот эндоморфизм быть
автоморфизмом линейного пространства
.
Может ли этот эндоморфизм быть
автоморфизмом линейного пространства ?
?**
 ,
где
,
где – конечномерное вещественное линейное
пространство, причем
– конечномерное вещественное линейное
пространство, причем удовлетворяет условию
удовлетворяет условию ,
т.е. для любого
,
т.е. для любого выполняется
выполняется .
Определите его собственные значения.
.
Определите его собственные значения.**
 ,
где
,
где – конечномерное вещественное линейное
пространство, причем
– конечномерное вещественное линейное
пространство, причем удовлетворяет условию
удовлетворяет условию ,
т.е. для любого
,
т.е. для любого выполняется
выполняется .
Определите его собственные значения.
.
Определите его собственные значения.*Может ли быть сумма двух собственных векторов
 сразличными
собственными
значениями быть собственным вектором
того же эндоморфизма?
сразличными
собственными
значениями быть собственным вектором
того же эндоморфизма?Пусть векторы
 и
и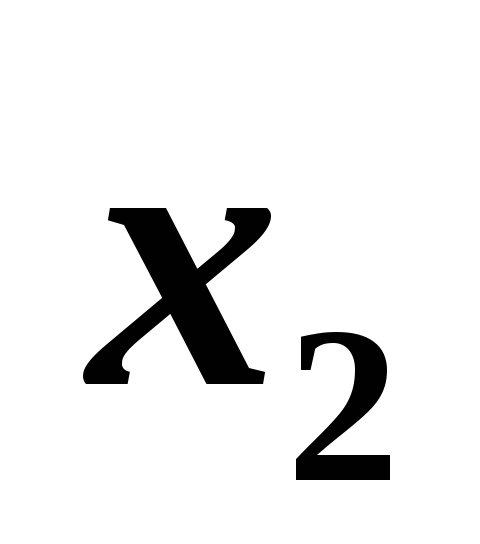 –
собственные
–
собственные с собственными значениями
с собственными значениями и, соответственно,
и, соответственно, .
Могут ли быть коллинеарными векторы
.
Могут ли быть коллинеарными векторы и
и ,
если
,
если ?
?Какие собственные векторы имеет линейный эндоморфизм
 ,
если относительно некоторого базиса
матрица
,
если относительно некоторого базиса
матрица ?
?*Эндоморфизм трехмерного линейного пространства имеет все собственные значения, равными
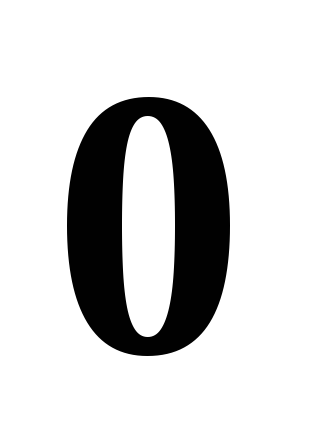 .
Означает ли это, что он является нулевым
эндоморфизмом, т.е.
.
Означает ли это, что он является нулевым
эндоморфизмом, т.е. для любого
для любого ?
?*Эндоморфизм трехмерного линейного пространства имеет все собственные значения, равные 1. Означает ли это, что он является тождественным эндоморфизмом, т.е.
 для любого
для любого ?
?Докажите, что собственные векторы эндоморфизма
 с различными собственными значениями
линейно независимы.
с различными собственными значениями
линейно независимы. имеет
имеет
 различных собственных значений.
Докажите, что из собственных векторов
с этими собственными значениями
составить базис
различных собственных значений.
Докажите, что из собственных векторов
с этими собственными значениями
составить базис .
Какова в этом базисе матрица эндоморфизма
.
Какова в этом базисе матрица эндоморфизма ?
?Может ли эндоморфизм линейного пространства иметь единственный собственный вектор?
Верно ли, что всякий эндоморфизм вещественного линейного пространства обязательно имеет собственные векторы (хотя бы один)?
Верно ли, что всякий эндоморфизм комплексного линейного пространства обязательно имеет собственные векторы (хотя бы один)?
Какова должна быть размерность конечномерного вещественного линейного пространства, чтобы любой его эндоморфизм имел бы, по крайней мере, один собственный вектор?
Укажите возможное наибольшее число собственных значений линейного оператора
 ?
?Укажите возможное наибольшее и наименьшее число линейно независимых собственных векторов линейного оператора
 ?
?Укажите возможное наибольшее и наименьшее число линейно независимых собственных направлений линейного оператора
 ?
?Пусть
 ,
а
,
а и
и –
его различные собственные значения.
Докажите, что
–
его различные собственные значения.
Докажите, что .
.Существует ли
 ,
где
,
где – вещественное линейное пространство,
для которого нет базиса, в котором его
матрица была бы диагональной?
– вещественное линейное пространство,
для которого нет базиса, в котором его
матрица была бы диагональной?Верно ли, что в любом подпространстве линейного пространства
 ,
инвариантного относительно
,
инвариантного относительно ,
имеется хотя бы один собственный вектор?
,
имеется хотя бы один собственный вектор?Верно ли, что в любом подпространстве линейного пространства
 ,
инвариантного относительно
,
инвариантного относительно ,
имеется хотя бы один собственный вектор?
,
имеется хотя бы один собственный вектор?Докажите, что
 является автоморфизмом
является автоморфизмом тогда и только тогда, когда характеристическое
уравнение
тогда и только тогда, когда характеристическое
уравнение не имеет нулевых корней.
не имеет нулевых корней.**Верно ли, что, если линейное пространство
 есть прямая сумма своих подпространств
есть прямая сумма своих подпространств и подпространство
и подпространство инвариантно относительно эндоморфизма
инвариантно относительно эндоморфизма ,
то подпространство
,
то подпространство также инвариантно относительно
также инвариантно относительно ?
?*Верно ли, что, если линейное пространство
 есть прямая сумма своих подпространств
есть прямая сумма своих подпространств и подпространство
и подпространство инвариантно относительно эндоморфизма
инвариантно относительно эндоморфизма ,
то подпространство
,
то подпространство также инвариантно относительно
также инвариантно относительно ?
? с матрицей
с матрицей
 .
Найдите
.
Найдите и
и .
.*Пусть
 и в некотором базисе
и в некотором базисе матрица
матрица диагональная. Верно ли, что в любом
подпространстве
диагональная. Верно ли, что в любом
подпространстве ,
инвариантном относительно
,
инвариантном относительно ,
найдется базис, относительно которого
ограничение
,
найдется базис, относительно которого
ограничение на подпространство
на подпространство имеет диагональную матрицу?
имеет диагональную матрицу?*Докажите, что, если для
 в некотором базисе матрица
в некотором базисе матрица диагональная, то
диагональная, то есть линейная оболочка всех собственных
векторов с ненулевыми собственными
значениями и
есть линейная оболочка всех собственных
векторов с ненулевыми собственными
значениями и .
.*Верно ли, что, если
 и имеет место
и имеет место ,
то найдется базис из собственных
векторов
,
то найдется базис из собственных
векторов ,
в котором матрица эндоморфизма
,
в котором матрица эндоморфизма диагональная?
диагональная? с матрицей
с матрицей
 .
Найдите
.
Найдите и
и .
. с матрицей
с матрицей
 .
Найдите
.
Найдите и
и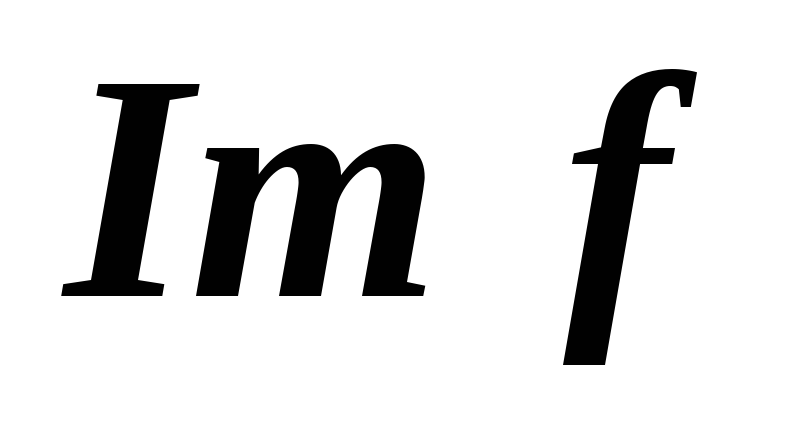 .
. с матрицей
с матрицей
 .
Найдите
.
Найдите и
и .
.*Существует ли
 ,
где
,
где –
вещественное линейное пространство,
в котором не существует базиса,
относительно которого его матрица была
бы диагональной?
–
вещественное линейное пространство,
в котором не существует базиса,
относительно которого его матрица была
бы диагональной? и является
ортогональным проектированием векторов
линейного пространства V
и является
ортогональным проектированием векторов
линейного пространства V на векторную прямую
на векторную прямую ,
заданную уравнениями:
,
заданную уравнениями: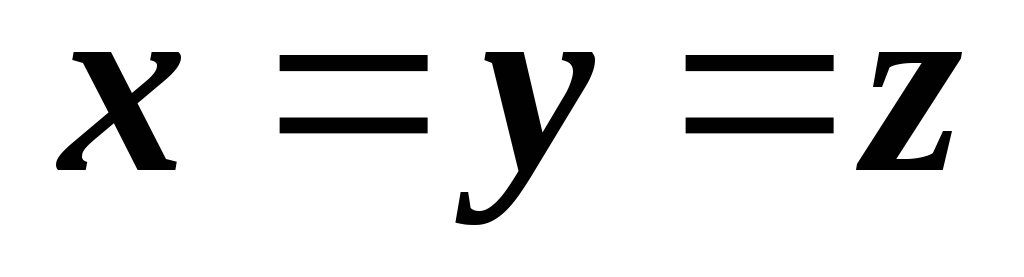 относительно некоторого ортонормированного
базиса. Найдите его матрицу
относительно некоторого ортонормированного
базиса. Найдите его матрицу относительно некоторого ортонормированного
базиса
относительно некоторого ортонормированного
базиса .
Существует ли базис, в котором матрица
.
Существует ли базис, в котором матрица диагональная?
диагональная? и является
ортогональным проектированием векторов
линейного пространства V
и является
ортогональным проектированием векторов
линейного пространства V на векторную прямую
на векторную прямую ,
заданную уравнениями:
,
заданную уравнениями: относительно некоторого ортонормированного
базиса. Найдите все его собственные
значения, собственные векторы и
собственные подпространства
относительно некоторого ортонормированного
базиса. Найдите все его собственные
значения, собственные векторы и
собственные подпространства .
. и является
ортогональным проектированием векторов
линейного пространства V
и является
ортогональным проектированием векторов
линейного пространства V на подпространство
на подпространство ,
заданное уравнением:
,
заданное уравнением:
 относительно некоторого ортонормированного
базиса
относительно некоторого ортонормированного
базиса .
Найдите его матрицу
.
Найдите его матрицу относительно этого базиса. Существует
ли базис, в котором матрица
относительно этого базиса. Существует
ли базис, в котором матрица диагональная?
диагональная? и является
ортогональным проектированием векторов
линейного пространства V
и является
ортогональным проектированием векторов
линейного пространства V на подпространство
на подпространство ,
заданное уравнением:
,
заданное уравнением:
 относительно некоторого ортонормированного
базиса
относительно некоторого ортонормированного
базиса .
Найдите все его собственные значения,
собственные векторы и собственные
подпространства.
.
Найдите все его собственные значения,
собственные векторы и собственные
подпространства.*
 и является поворотом на угол
и является поворотом на угол векторов линейного пространстваV
векторов линейного пространстваV вокруг векторной прямой
вокруг векторной прямой ,
заданной уравнениями:
,
заданной уравнениями: относительно некоторого ортонормированного
базиса
относительно некоторого ортонормированного
базиса .
Найдите его матрицу
.
Найдите его матрицу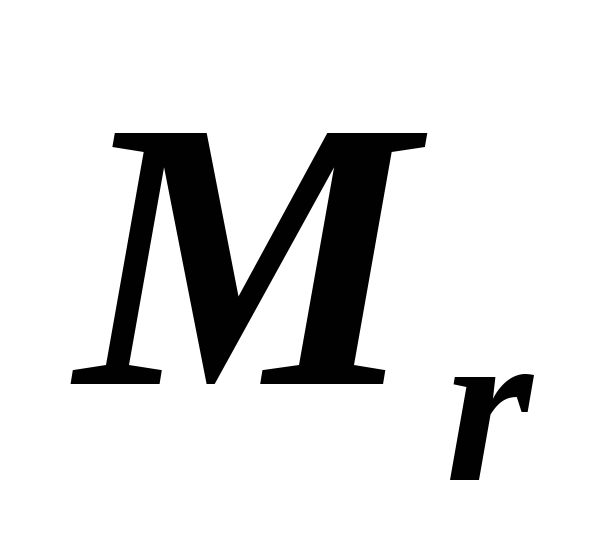 относительно этого базиса. Существует
ли базис, в котором матрица отображения
относительно этого базиса. Существует
ли базис, в котором матрица отображения диагональная?
диагональная?*
 и является поворотом векторов линейного
пространстваV
и является поворотом векторов линейного
пространстваV на угол
на угол вокруг векторной прямой
вокруг векторной прямой ,
заданной уравнениями:
,
заданной уравнениями: относительно некоторого ортонормированного
базиса
относительно некоторого ортонормированного
базиса .
Найдите все его собственные значения,
собственные векторы и собственные
подпространства
.
Найдите все его собственные значения,
собственные векторы и собственные
подпространства .
.*
 и является поворотом векторов линейного
пространстваV
и является поворотом векторов линейного
пространстваV на угол
на угол вокруг векторной прямой
вокруг векторной прямой ,
заданной уравнениями:
,
заданной уравнениями: относительно некоторого ортонормированного
базиса
относительно некоторого ортонормированного
базиса .
Найдите его матрицу
.
Найдите его матрицу относительно этого базиса. Существует
ли базис, в котором матрица
относительно этого базиса. Существует
ли базис, в котором матрица диагональная?
диагональная?*
 и является поворотом векторов линейного
пространстваV
и является поворотом векторов линейного
пространстваV на угол
на угол вокруг векторной прямой, заданной
уравнениями:
вокруг векторной прямой, заданной
уравнениями: относительно некоторого ортонормированного
базиса
относительно некоторого ортонормированного
базиса .
Найдите все его собственные значения,
собственные векторы и собственные
подпространства
.
Найдите все его собственные значения,
собственные векторы и собственные
подпространства .
.*
 и
и ,
где
,
где V
V ,
а
,
а – векторное произведение. Определите,
является ли
– векторное произведение. Определите,
является ли автоморфизмом линейного пространстваV
автоморфизмом линейного пространстваV .
.*
 и
и ,
где
,
где V
V ,
а
,
а – векторное произведение. Найдите
матрицу
– векторное произведение. Найдите
матрицу относительно базиса
относительно базиса .
Существует ли базис, в котором матрица
этого отображения
.
Существует ли базис, в котором матрица
этого отображения диагональная?
диагональная?*
 и
и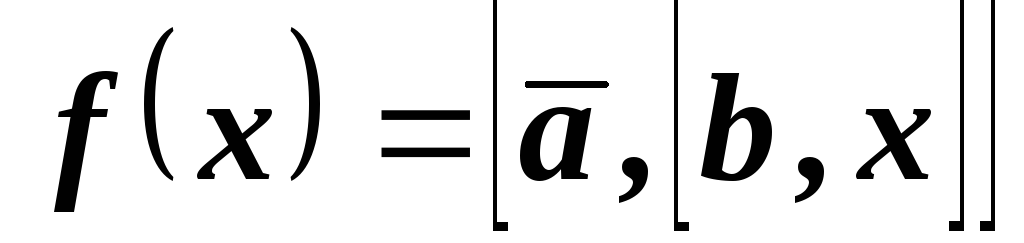 ,
где
,
где V
V ,
а
,
а – векторное произведение. Найдите
собственные векторы и собственные
подпространства
– векторное произведение. Найдите
собственные векторы и собственные
подпространства .
.Какие собственные векторы имеет
 ,
если относительно некоторого базиса
его матрица
,
если относительно некоторого базиса
его матрица ?
?*Пусть
 ,
где
,
где –
вещественное линейное пространство.
Верно ли, что в любом его подпространстве,
инвариантном относительно
–
вещественное линейное пространство.
Верно ли, что в любом его подпространстве,
инвариантном относительно ,
этот оператор имеет собственный вектор?
,
этот оператор имеет собственный вектор?Пусть
 ,
где
,
где –
конечномерное вещественное линейное
пространство. Верно ли, что в любом его
подпространстве, инвариантном
относительно
–
конечномерное вещественное линейное
пространство. Верно ли, что в любом его
подпространстве, инвариантном
относительно ,
этот оператор всегда имеет собственный
вектор?
,
этот оператор всегда имеет собственный
вектор?Пусть
 ,
где
,
где –
конечномерное вещественное линейное
пространство. Верно ли, что в любом
подпространстве
–
конечномерное вещественное линейное
пространство. Верно ли, что в любом
подпространстве нечетной размерности, инвариантном
относительно
нечетной размерности, инвариантном
относительно ,
этот оператор всегда имеет собственный
вектор?
,
этот оператор всегда имеет собственный
вектор? .
Верно ли, что если
.
Верно ли, что если
 имеет собственным вектором
имеет собственным вектором ,
то он является собственным вектором
линейного оператора
,
то он является собственным вектором
линейного оператора ?
? .
Верно ли, что если
.
Верно ли, что если
 имеет собственным вектором вектор
имеет собственным вектором вектор ,
то этот вектор – собственный вектор
линейного оператора
,
то этот вектор – собственный вектор
линейного оператора ?
? .
Верно ли, что если вектор
.
Верно ли, что если вектор
 – собственный вектор
– собственный вектор ,
то этот вектор – собственный вектор и
для линейного оператора
,
то этот вектор – собственный вектор и
для линейного оператора ?
?*
 и относительно некоторого базиса
и относительно некоторого базиса имеют матрицы
имеют матрицы и, соответственно,
и, соответственно, .
Верно ли, что характеристические
многочлены эндоморфизмов
.
Верно ли, что характеристические
многочлены эндоморфизмов и
и совпадают?
совпадают?*
 и относительно некоторого базиса
и относительно некоторого базиса имеют матрицы
имеют матрицы и, соответственно,
и, соответственно, .
Верно ли, что, если один из операторов
невырожденный (автоморфизм), например,
.
Верно ли, что, если один из операторов
невырожденный (автоморфизм), например, ,
то характеристические многочлены
эндоморфизмов
,
то характеристические многочлены
эндоморфизмов и
и совпадают?
совпадают?Пусть
 ,
и имеет собственный вектор
,
и имеет собственный вектор ,
,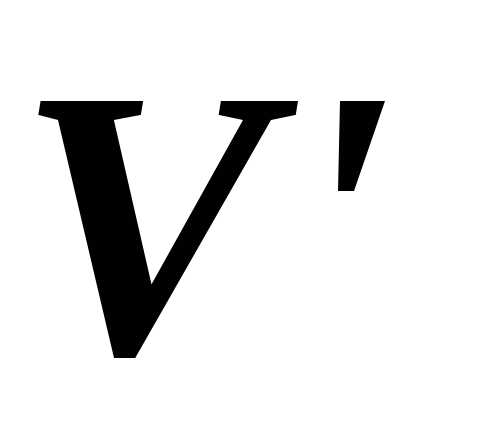 – дополнительное к
– дополнительное к подпространство
подпространство .
Является ли
.
Является ли инвариантным подпространством
относительно
инвариантным подпространством
относительно ?
?
