
- •(И особенно на потоке в.Т.Петровой)
- •1. Ранг матрицы, определитель матрицы
- •2. Системы линейных уравнений
- •2. Линейные пространства
- •3. Линейные отображения линейных пространств
- •4. Эндоморфизмы линейных пространств
- •5. Линейные формы на линейных пространствах
- •6. Билинейные и квадратичные формы на линейных пространствах
- •7. Скалярное произведение. Евклидово линейное пространство
- •8. Линейные операторы на евклидовых линейных пространствах
- •9. Квадратичные формы на евклидовых линейных пространствах
ОЧЕНЬ МНОГО ВОПРОСОВ
ПО КУРСУ ЛИНЕЙНОЙ АЛГЕБРЫ И ГЕОМЕТРИИ,
ПОЛЕЗНЫХ К РАЗМЫШЛЕНИЮ ПЕРЕД ЭКЗАМЕНОМ
(ОСОБЕННО ДОСРОЧНЫМ). СЕМЕСТР 2.
(И особенно на потоке в.Т.Петровой)
1. Ранг матрицы, определитель матрицы
Пусть
 M
M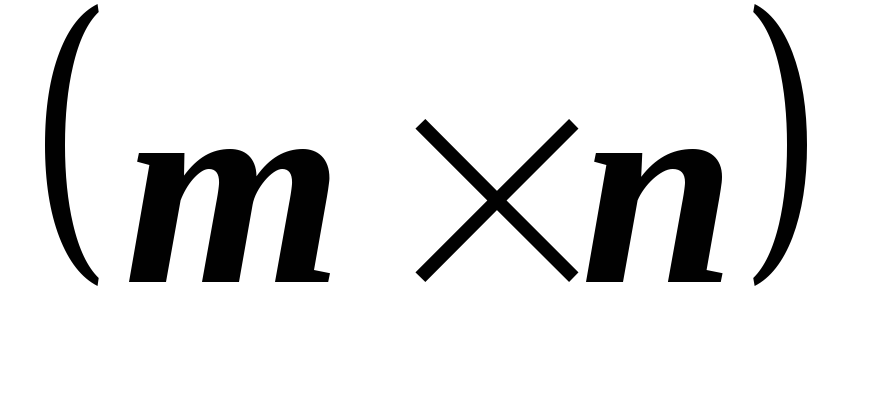 и строки этой матрицы линейно независимы.
Следует ли из этого, что
и строки этой матрицы линейно независимы.
Следует ли из этого, что
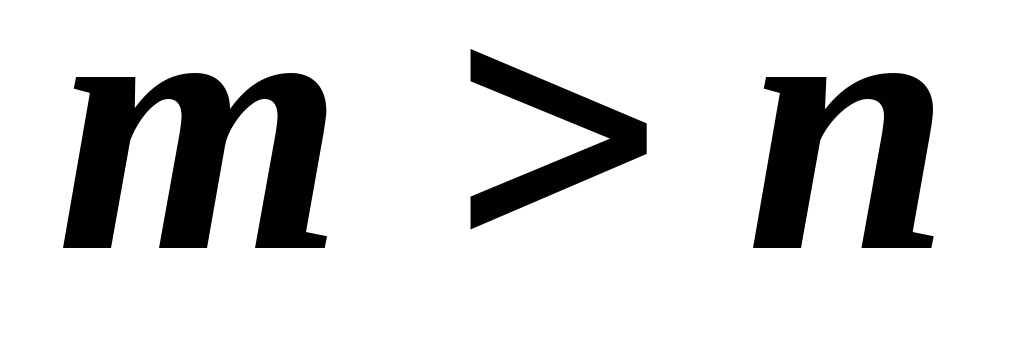 ?
?Пусть
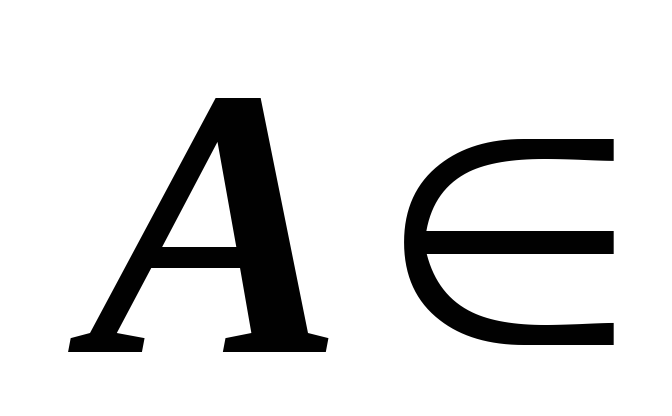 M
M и строки этой матрицы линейно зависимы.
Следует ли из этого, что
и строки этой матрицы линейно зависимы.
Следует ли из этого, что
 ?
?Пусть
 M
M и
и
 .
Следует ли из этого, что строки этой
матрицы линейно зависимы?
.
Следует ли из этого, что строки этой
матрицы линейно зависимы?Пусть
 M
M и
и
 .
Следует ли из этого, что строки этой
матрицы линейно независимы?
.
Следует ли из этого, что строки этой
матрицы линейно независимы?Пусть
 M
M и
и M
M ,
и матрицы
,
и матрицы
 и
и
 –
невырожденные, Верно ли, что и матрица
–
невырожденные, Верно ли, что и матрица
 –
тоже невырожденная?
–
тоже невырожденная?Пусть
 M
M и
и M
M ,
и матрица
,
и матрица
 –
невырожденная, Верно ли, что и матрицы
–
невырожденная, Верно ли, что и матрицы
 и
и
 – тоже
невырожденные?
– тоже
невырожденные?*Пусть
 M
M и
и M
M и матрица
и матрица
 –
невырожденная, Верно ли, что и матрица
–
невырожденная, Верно ли, что и матрица
 – тоже
невырожденная?
– тоже
невырожденная?*Пусть
 M
M и
и M
M и
и


 .Следует
ли из этого, что
.Следует
ли из этого, что
 и матрица
и матрица невырожденная?
невырожденная?Пусть строки матрицы
 M
M линейно зависимы и
линейно зависимы и .
Следует ли из этого, что
.
Следует ли из этого, что
 ?
?Пусть строки матрицы
 M
M линейно зависимы и
линейно зависимы и .
Следует ли из этого, что
.
Следует ли из этого, что
 ?
?Пусть
 M
M ,
причем строки матрицы
,
причем строки матрицы линейно независимы. Верно ли, что для
любой матрицы
линейно независимы. Верно ли, что для
любой матрицы M
M найдется матрица
найдется матрица ,
такая, что
,
такая, что ?
?Пусть
 M
M ,
причем столбцы матрицы
,
причем столбцы матрицы линейно независимы. Верно ли, что для
любой матрицы
линейно независимы. Верно ли, что для
любой матрицы M
M найдется матрица
найдется матрица ,
такая, что
,
такая, что ?
?Пусть
 M
M ,
а у матрицы
,
а у матрицы M
M линейно независимы строки. Верно ли,
что матрица
линейно независимы строки. Верно ли,
что матрица невырожденная?
невырожденная?Пусть
 M
M ,
а у матрицы
,
а у матрицы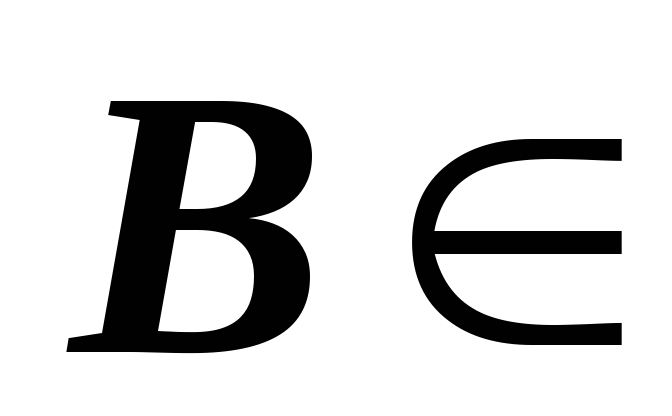 M
M линейно независимы строки. Верно ли,
что матрица
линейно независимы строки. Верно ли,
что матрица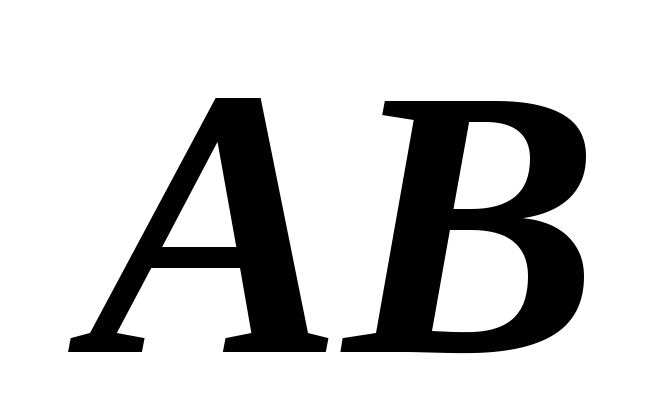 невырожденная?
невырожденная?*Пусть
 M
M и
и M
M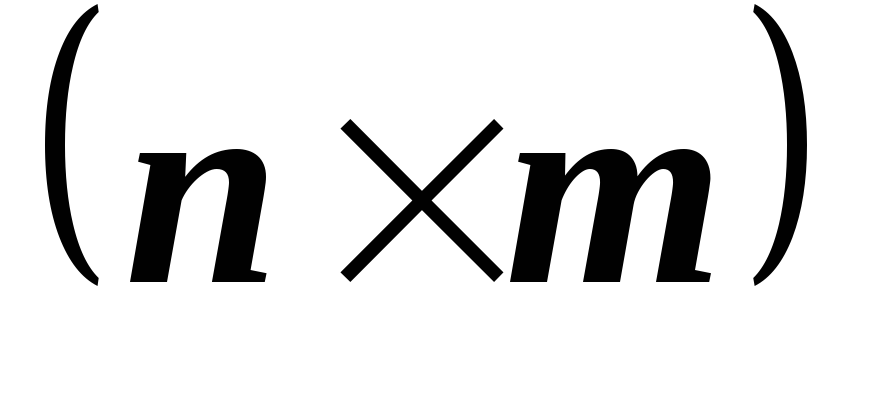 и матрица
и матрица
 –
невырожденная, Верно ли, что и матрица
–
невырожденная, Верно ли, что и матрица
 – тоже
невырожденная?
– тоже
невырожденная?**Пусть
 M
M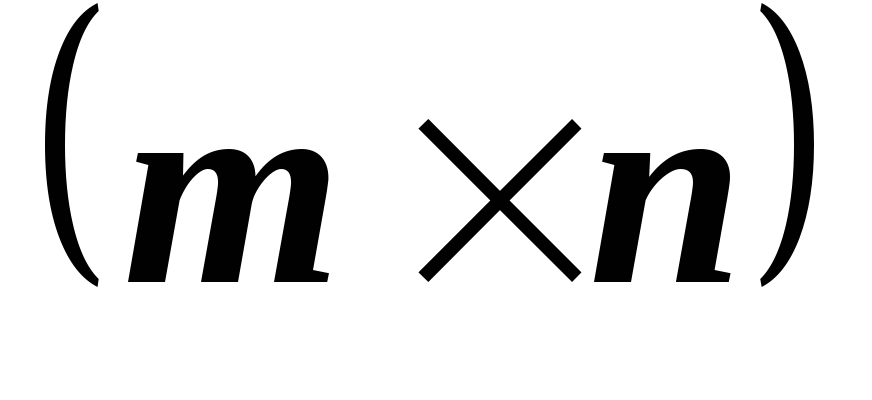 и
и M
M и
и
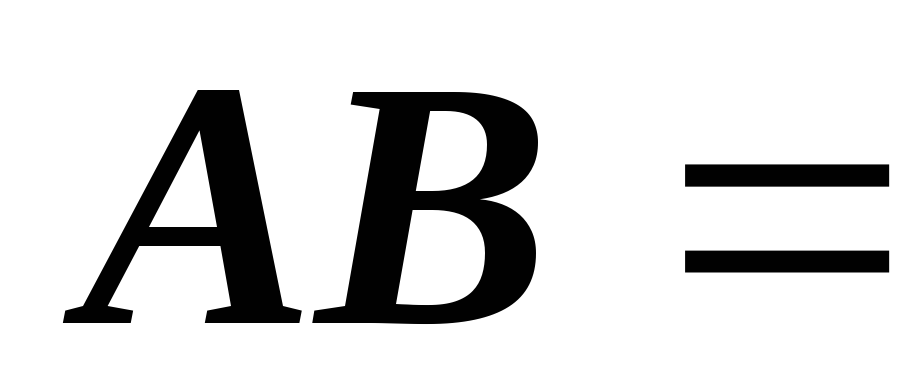

 .Следует
ли из этого, что
.Следует
ли из этого, что
 и матрица
и матрица невырожденная?
невырожденная?*Пусть
 M
M и ее столбцы линейно независимы, а
и ее столбцы линейно независимы, а M
M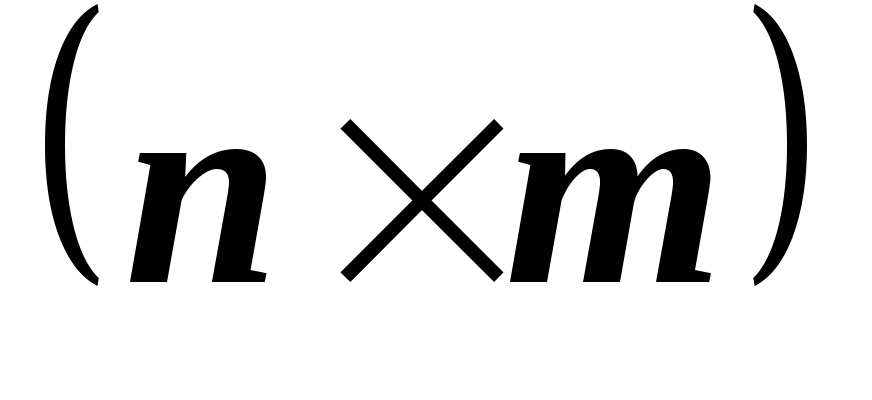 .
Верно ли, что в этом случае
.
Верно ли, что в этом случае


 ?
?*Пусть
 M
M и ее строки линейно независимы, а
и ее строки линейно независимы, а M
M .
Верно ли, что в этом случае
.
Верно ли, что в этом случае


 ?
?*Пусть
 M
M и
и .
Следует ли из этого, что
.
Следует ли из этого, что ?
?Пусть
 M
M и
и .
Следует ли из этого, что
.
Следует ли из этого, что ?
?Пусть
 M
M и
и .
Следует ли из этого, что
.
Следует ли из этого, что ?
?Пусть
 M
M и отличаются только порядком строк.
Верно ли, что их определители равны?
и отличаются только порядком строк.
Верно ли, что их определители равны?Пусть
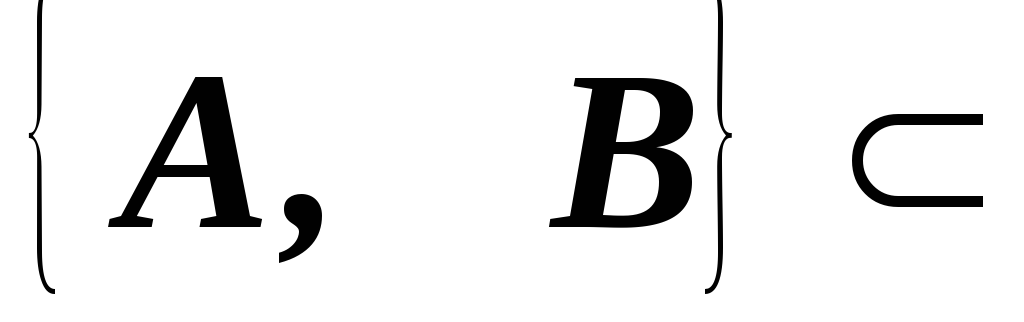 M
M и
и ,
а
,
а .
Следует ли из этого, что матрица
.
Следует ли из этого, что матрица – вырожденная?
– вырожденная?Пусть
 M
M – невырожденные. Следует ли из этого,
что
– невырожденные. Следует ли из этого,
что ?
?*Сравните ранги матриц
 и
и ,
где
,
где
 M
M .
.**Пусть
 M
M ,
верно ли, что квадратная матрица
,
верно ли, что квадратная матрица – всегда невырожденная?
– всегда невырожденная?*Сравните ранги матриц
 и
и ,
где
,
где
 M
M .
.
2. Системы линейных уравнений
Сколько решений может иметь система линейных уравнений
 ,
еслистолбцы
ее матрицы линейно независимы?
,
еслистолбцы
ее матрицы линейно независимы?Сколько решений может иметь система линейных уравнений
 ,
еслистроки
ее матрицы линейно независимы?
,
еслистроки
ее матрицы линейно независимы?В каком случае линейная неоднородная система уравнений
 из
из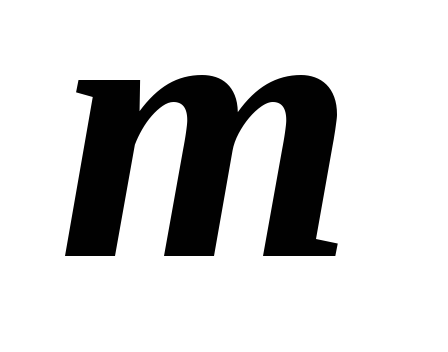 уравнений с
уравнений с переменными имеет единственное решение?
переменными имеет единственное решение?Пусть
 M
M ,
,
 M
M ,
а система уравнений
,
а система уравнений имеет единственное решение. Верно ли,
что в этом случае
имеет единственное решение. Верно ли,
что в этом случае ?
?Пусть
 M
M ,
,
 M
M ,
аX
– множество решений системы уравнений
,
аX
– множество решений системы уравнений
 .
Верно ли, что если множествоX
состоит
из конечного числа элементов, то
.
Верно ли, что если множествоX
состоит
из конечного числа элементов, то
 ?
?*Пусть
 M
M ,
,
 M
M ,
а система уравнений
,
а система уравнений имеет более одного решения. Верно ли,
что в этом случае
имеет более одного решения. Верно ли,
что в этом случае ?
?*Пусть
 M
M ,
,
 M
M ,
а система уравнений
,
а система уравнений имеет более одного решения. Верно ли,
что в этом случае
имеет более одного решения. Верно ли,
что в этом случае ?
?*Пусть
 M
M ,
,
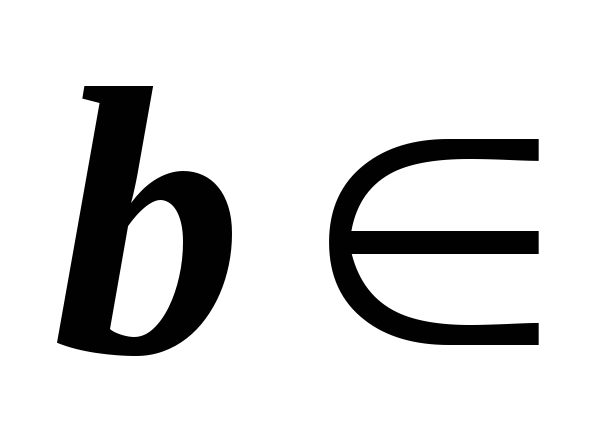 M
M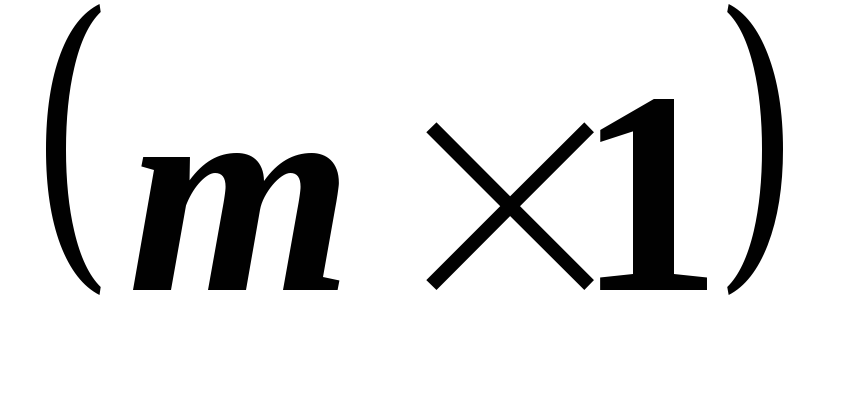 ,
причем столбцы матрицы
,
причем столбцы матрицы
 линейно зависимы. Следует ли из этого,
что система уравнений
линейно зависимы. Следует ли из этого,
что система уравнений
 имеет более одного решения?
имеет более одного решения?Пусть
 M
M ,
,
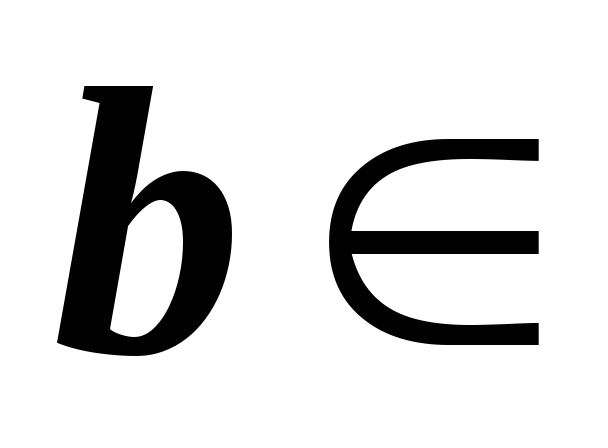 M
M ,
причем столбцы матрицы
,
причем столбцы матрицы
 линейно независимы. Следует ли из этого,
что система уравнений
линейно независимы. Следует ли из этого,
что система уравнений
 имеет более одного решения?
имеет более одного решения?Пусть строки матрицы
 M
M линейно зависимы, а система линейных
уравнений
линейно зависимы, а система линейных
уравнений имеет только нулевое решение. Следует
ли из этого, что
имеет только нулевое решение. Следует
ли из этого, что ?
?Пусть строки матрицы
 M
M линейно зависимы, а система линейных
уравнений
линейно зависимы, а система линейных
уравнений имеет ненулевое решение. Следует ли из
этого, что
имеет ненулевое решение. Следует ли из
этого, что ?
?Пусть
 M
M ,
а
,
а
 M
M ,
,
 M
M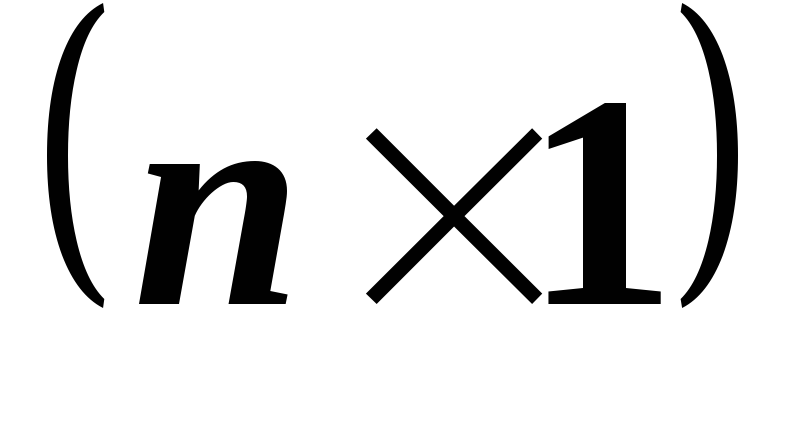 .
Верно ли, что если система линейных
уравнений
.
Верно ли, что если система линейных
уравнений несовместна, то хотя бы одна из систем
несовместна, то хотя бы одна из систем или
или также не имеет решений?
также не имеет решений?Пусть
 M
M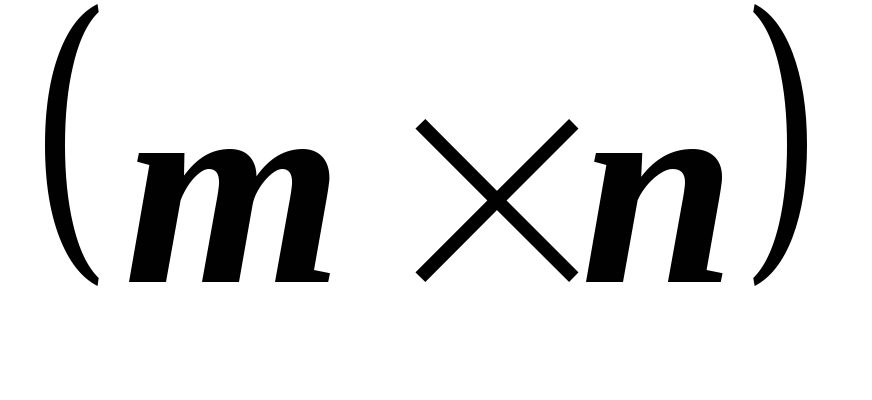 ,
а
,
а
 M
M ,
,
 M
M .
Верно ли, что если система линейных
уравнений
.
Верно ли, что если система линейных
уравнений совместна, то каждая из систем
совместна, то каждая из систем и
и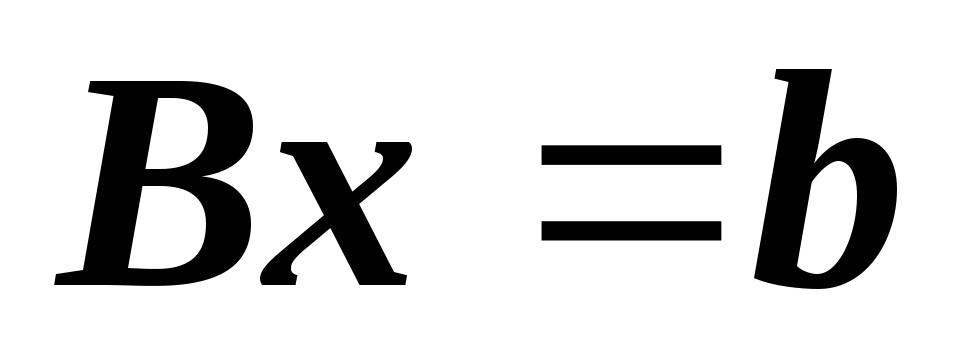 совместна?
совместна?Пусть
 M
M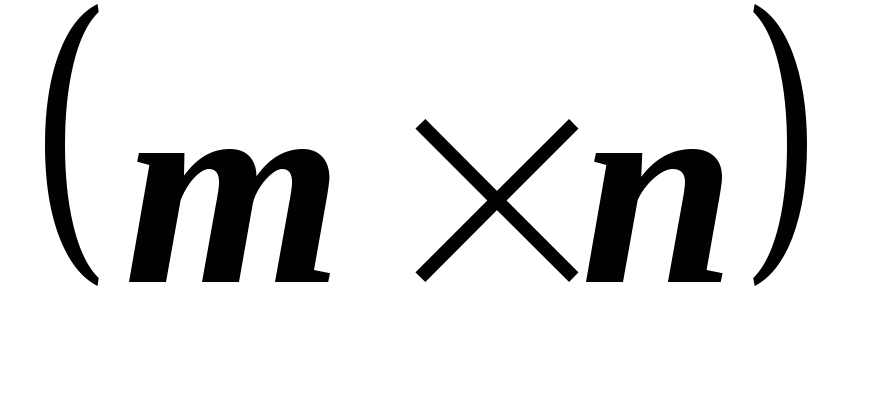 ,
а
,
а
 M
M ,
,
 M
M .
Верно ли, что если системы линейных
уравнений
.
Верно ли, что если системы линейных
уравнений и
и совместны, то и система
совместны, то и система совместна?
совместна?*Пусть
 M
M ,
а
,
а
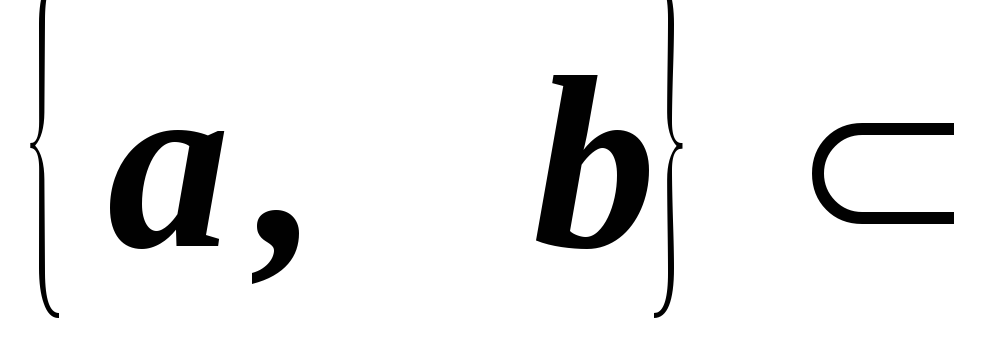 M
M ,
,
 M
M .
Верно ли, что если система линейных
уравнений
.
Верно ли, что если система линейных
уравнений несовместна, то хотя бы одна из систем
несовместна, то хотя бы одна из систем или
или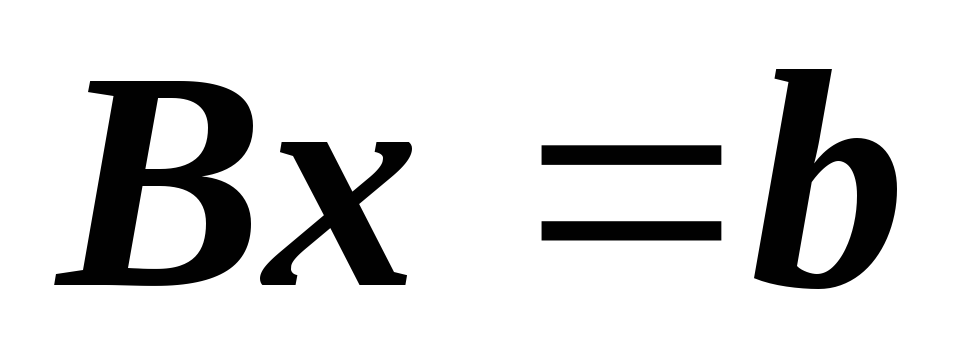 также несовместна?
также несовместна?**Пусть
 M
M ,
а
,
а
 M
M .
Верно ли, что если система линейных
уравнений
.
Верно ли, что если система линейных
уравнений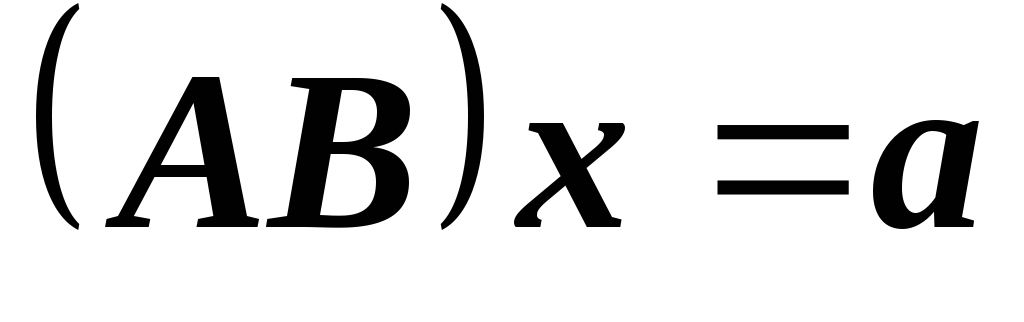 несовместна, а система
несовместна, а система совместна, то существует
совместна, то существует
 M
M ,
при котором система уравнений
,
при котором система уравнений несовместна?
несовместна?Могут ли векторы
 составлять фундаментальную систему
решений какой-либо системы линейных
однородных уравнений?
составлять фундаментальную систему
решений какой-либо системы линейных
однородных уравнений?Могут ли векторы
 составлять фундаментальную систему
решений какой-либо системы линейных
однородных уравнений?
составлять фундаментальную систему
решений какой-либо системы линейных
однородных уравнений?Могут ли векторы
 составлять фундаментальную систему
решений какой-либо системы линейных
однородных уравнений?
составлять фундаментальную систему
решений какой-либо системы линейных
однородных уравнений?Могут ли векторы
 составлять фундаментальную систему
решений какой-либо системы линейных
однородных уравнений?
составлять фундаментальную систему
решений какой-либо системы линейных
однородных уравнений?Известно, что векторы
 составляют фундаментальную система
решений некоторой системы линейных
однородных уравнений, верно ли, что
составляют фундаментальную система
решений некоторой системы линейных
однородных уравнений, верно ли, что –
фундаментальная система решений той
системы линейных уравнений?
–
фундаментальная система решений той
системы линейных уравнений?Известно, что векторы
 составляют фундаментальную систему
решений некоторой системы линейных
однородных уравнений. Верно ли, что
составляют фундаментальную систему
решений некоторой системы линейных
однородных уравнений. Верно ли, что –
фундаментальная система решений той
же системы линейных уравнений?
–
фундаментальная система решений той
же системы линейных уравнений?Пусть
 –
матрица фундаментальной системы решений
линейной однородной системы уравнений
с
–
матрица фундаментальной системы решений
линейной однородной системы уравнений
с переменными
переменными и
и –
столбец такой, что произведение
–
столбец такой, что произведение определено. Верно ли, что
определено. Верно ли, что есть также решение этой системы
уравнений?
есть также решение этой системы
уравнений?*Пусть
 –
матрица фундаментальной системы решений
системы линейных однородных уравнений.
Можно ли через матрицу
–
матрица фундаментальной системы решений
системы линейных однородных уравнений.
Можно ли через матрицу выразить любую из матриц ФСР этой
системы линейных уравнений?
выразить любую из матриц ФСР этой
системы линейных уравнений?**Пусть
 –
матрица фундаментальной системы решений
линейной однородной системы уравнений
–
матрица фундаментальной системы решений
линейной однородной системы уравнений .
Какова фундаментальная матрица системы
линейных однородных уравнений
.
Какова фундаментальная матрица системы
линейных однородных уравнений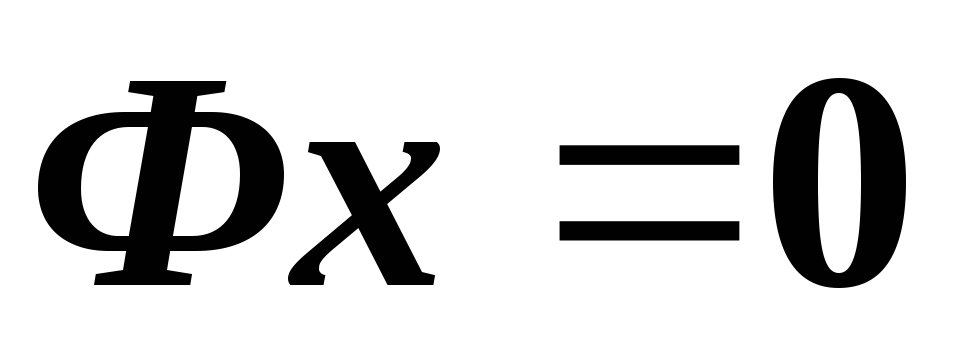 ?
?*Пусть
 –
матрица фундаментальной системы решений
линейной однородной системы уравнений
–
матрица фундаментальной системы решений
линейной однородной системы уравнений .
Какова фундаментальная матрица системы
линейных однородных уравнений
.
Какова фундаментальная матрица системы
линейных однородных уравнений ?
?**Пусть
 –
однородная система линейных уравнений,
причем число ее переменных
–
однородная система линейных уравнений,
причем число ее переменных больше ранга
больше ранга ее
матрицы
ее
матрицы .
Докажите, что в этом случае найдется
такая фундаментальная матрица ее
системы решений
.
Докажите, что в этом случае найдется
такая фундаментальная матрица ее
системы решений ,
что –
,
что – ,
где
,
где –
единичная матрица.
–
единичная матрица.*Пусть
 –
матрица фундаментальной системы решений
линейной однородной системы уравнений
с
–
матрица фундаментальной системы решений
линейной однородной системы уравнений
с переменными
переменными .
Определите ранг матрицы
.
Определите ранг матрицы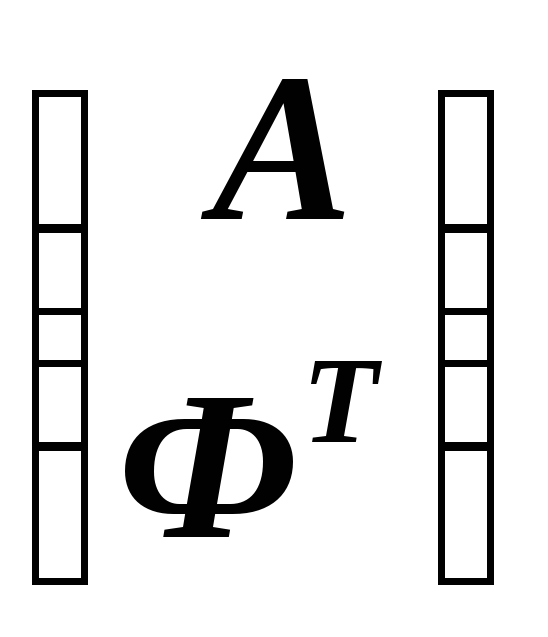 .
.Определите размерность пространства решений системы линейных уравнений:
 .
.Определите размерность пространства решений линейного уравнения:
 .
.Определите размерность пространства решений системы линейных уравнений:
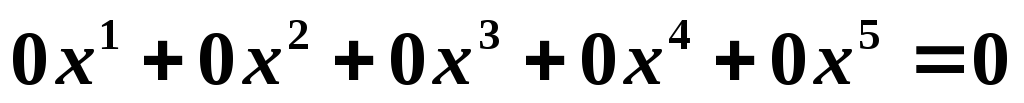 .
.Определите размерность пространства решений системы линейных уравнений:
 .
.Докажите, что если две совместные системы линейных уравнений эквивалентны, то их ранги равны.
*Докажите «альтернативу Фредгольма»: система линейных уравнений либо совместна при любом столбце свободных членов, либо ее сопряженная однородная система линейных уравнений имеет нетривиальное решение.
*Пусть присоединение одного уравнения к системе линейных уравнений не меняет множества решений. Докажите, что в этом случае присоединяемое уравнение есть линейная комбинация уравнений исходной системы уравнений.
**Для совместной системы линейных уравнений
 составлена система линейных уравнений:
составлена система линейных уравнений: .
Будет ли она тоже совместна?
.
Будет ли она тоже совместна?**Для несовместной системы линейных уравнений
 составлена система линейных уравнений:
составлена система линейных уравнений: .
Будет ли она совместна?
.
Будет ли она совместна?**Пусть
 M
M и
и M
M и система линейных уравнений
и система линейных уравнений имеет решение при любом
имеет решение при любом M
M .
Следует ли из этого, что
.
Следует ли из этого, что ?
?**Пусть
 M
M и
и M
M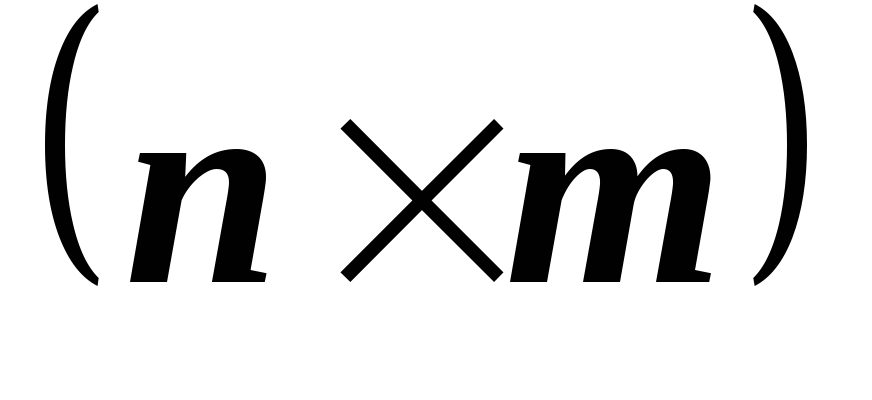 и система линейных уравнений
и система линейных уравнений имеет не более одного решения при каждом
имеет не более одного решения при каждом M
M .
Следует ли из этого, что
.
Следует ли из этого, что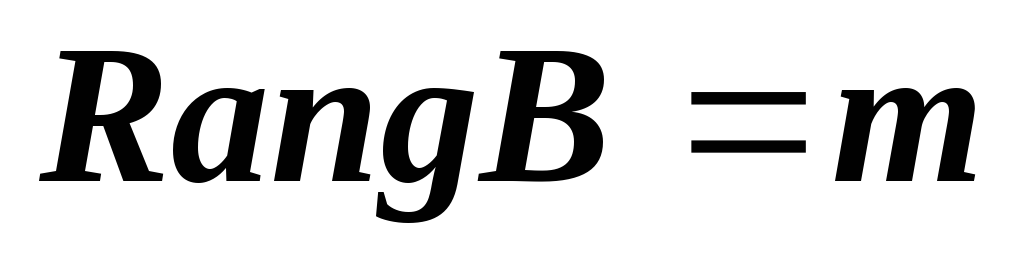 ?
?**Пусть
 M
M и
и M
M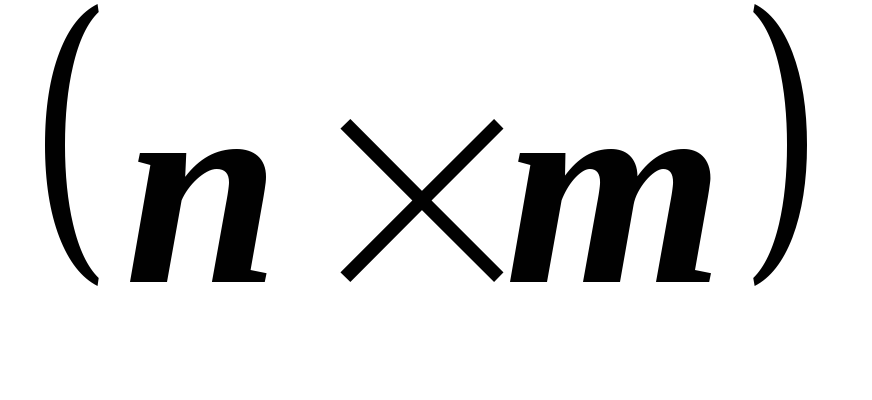 и система линейных уравнений
и система линейных уравнений имеет не более одного решения при каждом
имеет не более одного решения при каждом M
M .
Следует ли из этого, что
.
Следует ли из этого, что ?
?Пусть
 M
M и существует такой вектор
и существует такой вектор
 ,
что
,
что
 и
и .
Верно ли, что из этого следует, что
.
Верно ли, что из этого следует, что ?
?Пусть
 M
M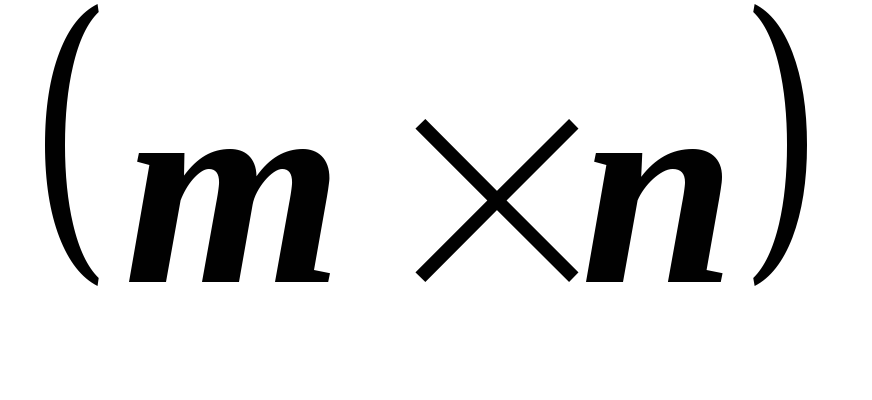 и существует такойненулевой
вектор
и существует такойненулевой
вектор
 ,
что
,
что
 и
и .
Верно ли, что из этого следует, что
.
Верно ли, что из этого следует, что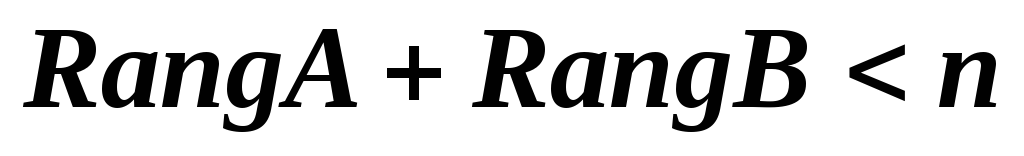 ?
?Пусть
 M
M и существует такойненулевой
вектор
и существует такойненулевой
вектор
 ,
что
,
что
 и
и .
Верно ли, что из этого следует, что
.
Верно ли, что из этого следует, что ?
?Пусть
 M
M и
система
линейных уравнений
и
система
линейных уравнений
 имеет только нулевое решение. Следует
ли из этого, что
имеет только нулевое решение. Следует
ли из этого, что ?
?Пусть
 M
M ,
а
,
а M
M – решения систем линейных уравнений
– решения систем линейных уравнений
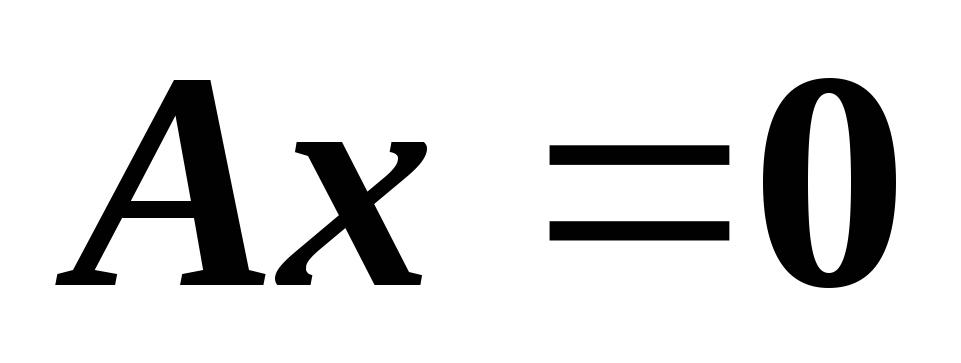 и, соответственно,
и, соответственно, ,
причем любой вектор
,
причем любой вектор
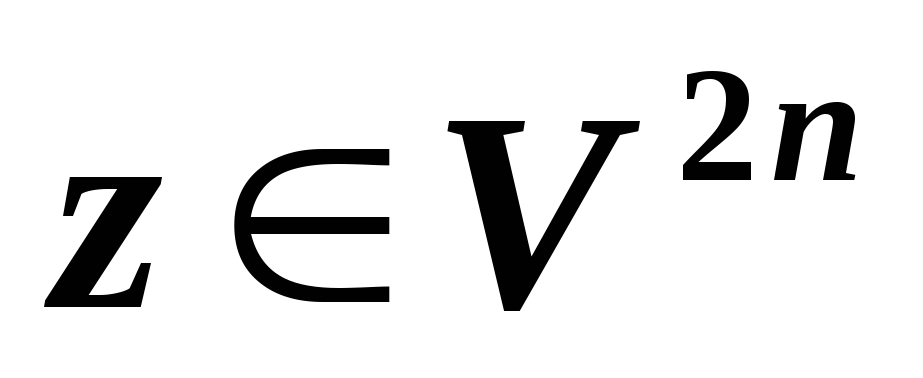 представим
в виде
представим
в виде
 ,.
Следует ли из этого что
,.
Следует ли из этого что
 ?
?Запишите решение матричного уравнения
 при условии, что матрицы
при условии, что матрицы и
и квадратные и невырожденные (обратимые).
квадратные и невырожденные (обратимые).
