III. Современные методы обработки спектроскопических данных

Супрамолекулярная химия – это химия сравнительно слабых нековалентных взаимодействий. Супрамолекулярные системы часто представляют собой равновесную смесь реагентов и продуктов. Поэтому важной задачей является определение числа компонентов в исследуемой системе. Эту задачу можно решить, используя современные методы глобального анализа спектроскопических данных, например, абстрактный факторный анализ. Методы глобального анализа, такие как параметрическое моделирование спектров, незаменимы в тех случаях, когда нужно определить неизвестные спектры отдельных компонентов реакционной смеси.

Абстрактный факторный анализ

Этот метод применяется для определения числа линейно независимых компонентов в системе. Рассмотрим его в применении к электронным спектрам поглощения.

Допустим, что спектры поглощения реакционной системы изменяются в зависимости от определенного фактора, например, от концентрации реагентов. Спектры, измеренные при разных концентрациях реагентов в фиксированном спектральном диапазоне с одинаковым шагом, можно представить в виде матрицы данных D_exp размерности n ´ m, где n – число значений оптической плотности в спектре, m – число измеренных спектров.

Чтобы определить число поглощающих свет компонентов в системе, матрицу D_exp подвергают разложению по сингулярным числам и сингулярным векторам. Такое разложение удобно проводить с помощью программы Matlab (версия 6 или 7, MathWorks, Inc.), встроенные функции которой позволяют легко оперировать с матрицами данных. Например, операция сингулярного разложения матрицы данных D_exp размерности n ´ m выполняется с помощью функции ‘svd’, генерирующей три матрицы

[V,S,U] = svd(D_exp),

где V – матрица размерности n  n с искомыми векторами сингулярного разложения в порядке убывания значимости, S – матрица размерности n  m с неотрицательными диагональными элементами в порядке убывания (сингулярными значениями), U – унитарная матрица размерности m  m такая, что

D_exp = VSU',

где U' – транспонированная матрица U.

Сингулярные векторы обладают замечательным свойством – если реакционная система содержит k поглощающих свет компонентов, то спектры поглощения этой системы, измеренные при разных концентрациях реагентов, можно представить в виде линейной комбинации первых k векторов сингулярного разложения матрицы данных D_exp. Остальные векторы описывают погрешности измерения спектров.

Наилучшая аппроксимация матрицы данных D_exp с помощью первых k векторов сингулярного разложения находится по формуле

D_svd = V(1:n,1:k)S(1:k,1:m)U',

где V(1:n,1:k) – матрица, составленная из первых k столбцов матрицы V, а S(1:k,1:m) – матрица, составленная из первых k строк матрицы S.

Погрешность, с которой теоретическая матрица D_svd воспроизводит матрицу данных D_exp, определяется среднеквадратичным отклонением

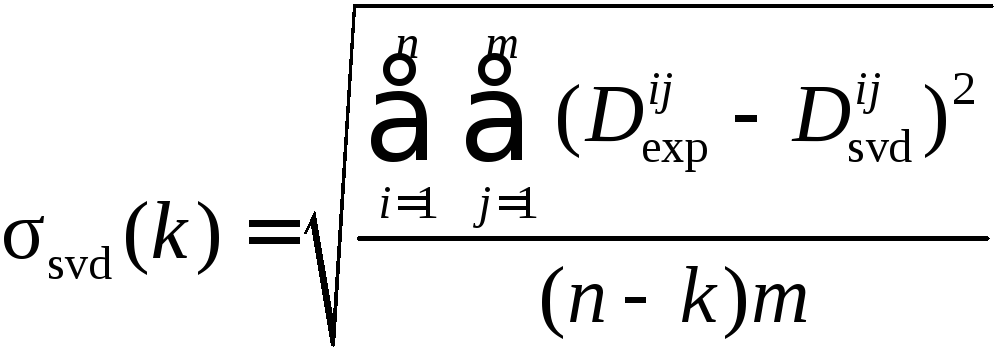
Количество поглощающих свет компонентов в системе определяется по минимальному значению k, при котором величина стандартного отклонения s_svd снижается до уровня инструментальной погрешности измерения спектров.

Если речь идет о спектрофотометрических данных, то инструментальная погрешность обычно очень мала: ~ 10^–4 ед. оптической плотности.

Реализация абстрактного факторного анализа в программе Matlab

% Загружаем матрицу экспериментальных спектров, находящуюся,

% например, в файле “spectra.dat”

load spectra.dat -ascii; [a,b]=size(spectra);

% Берем из файла “spectra.dat” столбец со значениями длины волны

% и столбцы со значениями оптической плотности

Wavelength=spectra(1:a,1:1); Dexp=spectra(1:a,2:b); [n,m]=size(Dexp);

% Выводим спектры на экран

plot(Wavelength, Dexp);

% Производим сингулярное разложение

[V,S,U]=svd(Dexp);

% Находим теоретическую матрицу спектров Dcal, воспроизводящую

% матрицу Dexp с помощью первых k векторов сингулярного разложения

% (k = 1–5), а также стандартное отклонение между Dexp и Dcal

for i=1:5; Dcal=V(:,1:i)*S(1:i,:)*U';

Standard_Deviation(i)=(sum(sum((Dcal-Dexp).^2))/(n-i)/m)^0.5;

end;

% Выводим на экран стандартное отклонение

Standard_Deviation

Параметрическое моделирование спектров

Метод параметрического моделирования спектров (ПМC) незаменим при количественном исследовании сложных многокомпонентных систем, в частности, супрамолекулярных систем. Допустим, что для данной системы мы измерили спектры поглощения в зависимости от определенных факторов, например, от концентрации реагентов. Параметрическое моделирование экспериментальных спектров производится на основе предполагаемой реакционной модели. Метод ПМС дает возможность проверить справедливость модели и, если она верна, определить неизвестные спектры отдельных компонентов системы, а также количественные характеристики реакций. Рассмотрим этот метод в применении к данным спектрофотометрического титрования (СФТ) для системы лиганд/катион металла.

Обычно данные СФТ представляют собой набор спектров поглощения, измеренных при постоянной общей концентрации лиганда (C_L) и переменной общей концентрации катиона металла (C_M).

Экспериментальные спектры поглощения представляются в виде матрицы D_exp, которая может включать данные сразу нескольких экспериментов, проведенных при разной величине C_L в кюветах разной длины l. Допустим, что для исследуемой системы применима реакционная модель, включающая две равновесные реакции:

где L – молекула лиганда, M – катион металла, K₁ и K₂ – константы равновесия. Допустим, что поглощающими свет компонентами в данной системе являются только L, LM и LM₂. Используя закон действующих масс и принцип материального баланса, составляем систему уравнений:

[LM] = K₁ [L] [M]

[LM₂] = K₂ [LM] [M]

C_L = [L] + [LM] + [LM₂]

C_M = [M] + [LM] + 2 [LM₂]

Процесс ПМС начинается с постулирования значений констант равновесия K₁ и K₂ и решения вышеуказанной системы уравнений, которая легко сводится к уравнению третьей степени для [L],

K₁(4K₂–K₁)[L]³+K₁(K₁C_L–K₁C_M–8K₂C_L+4K₂C_M)[L]²+(4K₁K₂C_L²–4K₁K₂C_LC_M+K₁K₂C_M²+K₁C_M+1)[L]–C_L=0.

Это уравнение имеет аналитическое решение. Правильный корень кубического уравнения выбирается, исходя из физических ограничений для концентраций компонентов. В более сложных случаях концентрации компонентов можно рассчитать численным методом.

Найденные величины концентраций [L], [LM] и [LM₂] умножаются на соответствующее значение длины кюветы l и составляется матрица "концентраций" C размерности 3 ´ m, первую строку которой составляют значения [L]l, вторую – значения [LM]l, и третью – значения [LM₂]l.

Затем путем решения матричного выражения закона поглощения света

D = EC

генерируется теоретическая матрица коэффициентов молярного поглощения компонентов E_cal размерности n ´ 3

E_cal = D_expC'(CC')^–1,

где C' – транспонированная матрица C. Теоретическая матрица D_cal, воспроизводящая матрицу D_exp, вычисляется по формуле

D_cal = E_calC.

Константы равновесия K₁ и K₂, а также коэффициенты молярного поглощения всех трех поглощающих свет компонентов, то есть L, LM и LM₂, находятся путем минимизации стандартного отклонения s_D(K₁,K₂) между теоретической матрицей D_cal и матрицей экспериментальных данных D_exp. Выражение для s_D аналогично выражению для погрешности s_svd. Величина s_D является критерием справедливости реакционной модели. Помимо инструментальных погрешностей она включает погрешности, связанные со случайными и систематическими ошибками измерения концентраций реагентов, и, следовательно, зависит не только от точности оборудования, но и от методики эксперимента. Обычно, величина s_D не должна превышать 0.002 ед. оптич. плотности.

Метод ПМС очень легко реализуется с помощью программы Matlab !!!

За бесплатными примерами реализации этого метода обращайтесь по email: